| CATEGORII DOCUMENTE | ||
|
||
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Tensiunea electrica. Potential
Tensiunea electrica este o marime derivata, definita
cu ajutorul vectorului ![]() .
.
Considerand un camp de intensitate ![]() (fir. 2.5) lucrul mecanic necesar pentru
deplasarea sarcinii q intre punctele A si B este:
(fir. 2.5) lucrul mecanic necesar pentru
deplasarea sarcinii q intre punctele A si B este:
![]() (2.23)
(2.23)

Fig. 2.5.
Tinand seama de exprimarea fortei ![]() , functie de
intensitatea campului electric in vid
, functie de
intensitatea campului electric in vid ![]() rezulta:
rezulta:
![]() (2.24)
(2.24)
Raportul ![]() , notat
, notat ![]() se numeste tensiune electrica:
se numeste tensiune electrica:
![]() (2.25)
(2.25)
Enunt: "Tensiunea electrica intre doua puncte din camp este egala cu lucrul mecanic efectuat de fortele campului neutru deplasarea sarcinii electrice unitare intre cele doua puncte".
Tensiunea electrica se masoara in volti (V).
Un volt este tensiunea intre doua puncte din camp pentru care se cheltuie lucru mecanic de un joule (J) la deplasarea sarcinii de un coulomb (C) intre aceste puncte.
Relatia (2.24) defineste si unitatea de masura a
intensitatii campului electric: volt pe metru ![]()
Din definitie se vede ca ![]() , deci
tensiunea electrica depinde de sensul de integrare. Acest sens, numit sens de
referinta, se indica printr-o sageata, de exemplu la bornele unui circuit
(fug.2.6).
, deci
tensiunea electrica depinde de sensul de integrare. Acest sens, numit sens de
referinta, se indica printr-o sageata, de exemplu la bornele unui circuit
(fug.2.6).
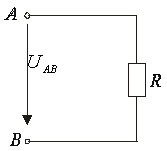
Fig. 2.6.
O proprietate importanta a tensiunii electrice in camp
electrostatic este aceea ca valoarea ei nu depinde de drum ci numai de
extremitatile A,B considerate. Luand conturul inchis ![]() (fig. 2.7) rezulta:
(fig. 2.7) rezulta:
![]() (2.26)
(2.26)
relatie valabila pentru campuri care deriva dintr-un potential.
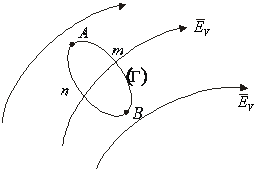
Fig. 2.7.
Descompunand conturul ![]() pe portiuni se obtine:
pe portiuni se obtine:
![]() (2.27)
(2.27)
sau
![]() (2.28)
(2.28)
deci tensiunea electrica nu depinde de drum.
Daca se alege in spatiu, in mod arbitrar, un punct P, atunci valoarea integralei:
![]() (2.29)
(2.29)
se numeste potentialul punctului A.
In mod similar se defineste si potentialul altor puncte din camp:
![]() ,
, 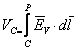 , etc.
, etc.
Potentialul punctului p este zero, deoarece:
![]() (2.30)
(2.30)
Enunt: "Potentialul electric intr-un punct dat al campului electrostatic este numeric egal cu lucrul mecanic efectuat de fortele campului pentru deplasarea sarcinii unitare din punctul considerat intr-un alt punct al carui potential este zero".
Potentialul electric, V, este o marime fizica de
natura scalara ce caracterizeaza nivelul local de electrizare. In regimul
electrostatic potentialul electric (electrostatic) este functie numai de
spatiu, ![]() , deci
invariabil in timp.
, deci
invariabil in timp.
Observatie
In cazul general al regimului nestationar, valoarea potentialului se modifica atat de la un punct la altul al campului electric (deci este functie de spatiu) cat si in timp (este functie si de timp).
Este cunoscut faptul ca in campul gravitational energia potentiala a unui corp se stabileste in functie de pozitia corpului in raport cu o cota de referinta, de exemplu fata de nivelul marii (cota zero).
Tot asa, valoarea potentialului intr-un punct din campul electric se poate stabili numai in raport cu un potential electric de referinta.
Se considera drept potentiale electrice de referinta potentialul pamantului sau potentialul in punctele situate la distanta foarte mare de corpurile electrizate (la infinit).
Valoarea potentialului pamantului, precum si a tuturor corpurilor metalice legate la pamant se considera, conventional, egala cu zero. Tot conventional este considerat egal cu zero potentialul punctelor situate la infinit.
Daca campul electrostatic este produs in vid de un
singur corp punctiform incarcat cu sarcina electrica q, potentialul electric
intr-un punct P situat la distanta r de corp este: ![]()
adica:
![]() (2.31)
(2.31)
unde s-au inlocuit ![]() ,
, ![]()
Din relatia (2.31) se remarca faptul ca potentialul electric intr-un punct al campului produs de o sarcina electrica punctiforma este direct proportional cu sarcina si invers proportional cu distanta de la sarcina la punct. La infinit potentialul electric rezulta egal cu zero.
Unitatea de masura pentru potentialul electric se numeste volt (simbolul V).
Cu ajutorul voltmetrului se masoara in campul
electrostatic intotdeauna o diferenta de potential (tensiune electrica) intre
doua punct (borne): ![]()
Chiar si atunci cand unul din cele doua puncte este legat la pamant (masa), voltmetrul masoara, nu potential electric, ci diferenta de potential fata de pamant.
Suprafetele pentru care toate punctele lor au potential se numesc echipotentiale.
Ecuatia suprafetelor echipotentiale se deduce din conditia:
![]() (2.32)
(2.32)
care prin definitie devine:
![]() (2.33)
(2.33)
Relatia (2.33) care reprezinta ecuatia diferentiala a suprafetelor echipotentiale, arata ca suprafetele echipotentiale sunt perpendiculare pe liniile de camp.
I n figura 2.8. sunt reprezentate cateva exemple. Cu linie plina s-au reprezentat liniile de camp, iar cu liniile intrerupte suprafetele echipotentiale.
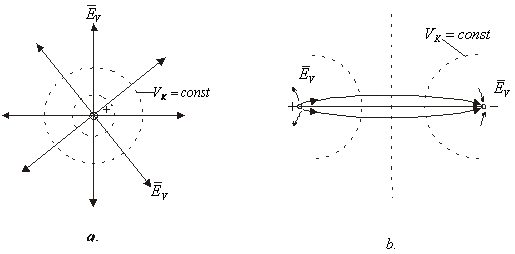
Fig. 2.8
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2233
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved