CONTROLUL CALITATII - Controlul calitatii produselor

CONTROLUL CALITATII

1. Controlul calitatii produselor

1.1. Terminologie si obiective

Conform SR EN ISO 9000-2001 Controlul calitatii este parte a managementului calitatii concentrata pe indeplinirea cerintelor referitoare la calitate.

Inspectia calitatii reprezinta evaluarea conformitatii prin observare si judecare insotite dupa caz, de masurare, incercare sau comparare cu un calibru.

Verificarea calitatii este confirmarea prin furnizare de dovezi obiective, ca au fost indeplinite cerintele specificate.

Conformitate reprezinta indeplinirea unei cerinte (nevoie declarata implicita sau obligatorie).

In mod uzual insa prin control al calitatii, se intelege totalitatea actiunilor de determinare a caracteristicilor produselor in conformitate cu documente tehnice normative elaborate in acest scop, definitie mai apropiata de cea inspectiei calitatii.

In trecut controlul se reducea la verificarea principalelor operatii pe fluxul de fabricatie si la controlul produsului finit. Astazi controlul trebuie sa aiba un caracter activ, intervenind la timp si eficient in desfasurarea procesului de productie, ca un factor dinamic in realizarea calitatii.

Metodele de organizare a controlului au evoluat in timp datorita complexitatii, sporirii preciziei si randamentului proceselor tehnologice (fig. 1.) [19].

1900 1920 1930 1960 1980 1990

Figura 1. Evolutia in timp a metodelor de control

Obiectivele controlului calitatii s-au schimbat si au evoluat in timp. Daca la inceput controlul executantului si al maistrului avea obiective simple, legate de conformitatea produsului, in urmatoarele etape de dezvoltare, obiectivele au devenit din ce in ce mai complexe, astfel [25]:

obiectivele serviciului CTC sunt:

conformitatea produsului cu prescriptiile documentatiei tehnologice;

asigurarea calitatii produselor fata de prevederile contractelor;

obiectivele controlului statistic sunt:

fundamentarea stiintifica a deciziilor privind:

acceptarea sau refuzul produselor (receptie);

continuarea, corectarea sau intreruperea procesului de productie;

reducerea cheltuielilor de control;

obiectivele controlului total sunt:

cresterea nivelului calitatii produselor;

perfectionarea produsului;

perfectionarea organizarii fabricatiei;

gestiunea calitatii si cresterea raspunderii operatorilor.

1.2 Metode de control in raport cu fluxul de fabricatie

Pentru buna desfasurare a proceselor de fabricatie se impune introducerea unor operatii de control care sa confirme corectitudinea desfasurarii operatiilor tehnologice de prelucrare si, implicit, a intregului proces tehnologic. In prezent in functie de fluxul de fabricatie se utilizeaza urmatoarele metode principale de control

Autocontrolul

Autocontrolul este o metoda de control cu caracter individual.

Denumita si controlul executantului, aceasta metoda este cea mai veche si cea mai eficienta metoda de control.

Pentru aplicarea autocontrolului, executantul trebuie sa cunoasca:

operatia pe care trebuie sa o execute;

modalitatea de control a operatiei executate.

Avand in vedere importanta si nivelul tehnic al operatiei de control rezulta ca muncitorul trebuie sa indeplineasca urmatoarele conditii:

- sa fie bine pregatit profesional;

- sa fie obiectiv si constiincios.

Autocontrolul nu exclude controlul organismelor specializate. In acest fel creste raspunderea executantului in ceea ce priveste efectuarea controlului si luarea deciziilor.

Autocontrolul se poate aplica in cadrul proceselor tehnologice neautomatizate, nestabilizate, in orice proces de fabricatie, la orice produs sau serviciu, de la cel mai simplu reper la cel mai complex produs.

Controlul in lant

Aceasta metoda are caracter individual dar si colectiv.

Este o varianta evoluata a autocontrolului, care se poate aplica numai intr-un proces de fabricatie in serie sau pe banda.

In acest caz, muncitorul, pe langa controlul executat asupra propriei operatii efectuate, controleaza si operatia efectuata de muncitorul de la care a primit piesa. La randul sau muncitorul va fi controlat de catre cel care va primi piesa executata de el si asa mai departe - in lant - fiecare operatie va fi controlata de doua ori.

Executantul care lucreaza intr-o echipa care aplica controlul in lant trebuie sa cunoasca:

operatia de control a operatiei anterioare;

executia operatiei proprii;

controlul propriei operatii.

Controlul la puncte fixe

In anumite puncte ale procesului de fabricatie se executa operatii de control al reperelor, subansamblurilor sau operatiilor, in functie de importanta acestora in continuitatea procesului de fabricatie:

pentru parametrii care nu mai pot fi verificati la controlul final;

pentru parametrii deosebit de importanti in asigurarea calitatii produsului finit;

pentru parametrii care fiind in afara limitelor admise ar conduce la pierderi economice foarte mari.

Acest control este executat de personal specializat.

Controlul final

Aceasta este cea mai importanta forma de control, deoarece ea permite acordarea calificativului admis/ respins pentru produsul controlat, la incheierea procesului de fabricatie.

In acelasi timp, el reprezinta ultima sansa a producatorului de a verifica in intregime conformitatea produselor cu cerintele clientului.

Functie de importanta si calitatea produselor controlul final poate fi facut bucata cu bucata, pe baze statistico - matematice (prin esantionare) sau prin alte metode prevazute in contract.

Numarul caracteristicilor verificate depinde de gradul de complexitate si importanta produsului controlat.

Personalul care executa controlul final este special calificat.

1.3 Metode de control in raport cu volumul controlat

Controlul integral sau 100%

Aceasta metoda, foarte raspandita, presupune controlul bucata cu bucata a intregii cantitati de produse.

Desi acest control are mai multe avantaje la productia de unicate sau de serie mica, precum si in cazul unei productii nestabilizate, el intruneste cateva neajunsuri la productia in serie mare sau in masa, cunoscute sub denumirea de regula celor 4N.

N1 controlul integral este Neeconomic.

Odata cu cresterea volumului controluliui cresc: numarul de controlori, cantitatea de mijloace de control, timpul afectat controlului ceea ce inseamna cheltuieli din ce in ce mai mari.

N2 - controlul integral este Neaplicabil in cazul controlului distructiv.

Exista metode de control distructiv cand integritatea obiectului controlat este afectata ceea ce il face inutilizabil. Este clar ca acestui tip de control nu i se poate asocia controlul 100%.

N3 - controlul integral este Nefiabil.

Controlorii care executa de sute si mii de ori aceeasi operatie manifesta scaderea puterii de percepere datorita oboselii, plictiselii, rutinei, ceea ce conduce la erori in luarea deciziilor.

Studiile efectuate au condus la concluzia ca fiabilitatea controlului integral depinde de:

tipul caracteristicii masurate;

felul mijloacelor de masurare;

conditiile si in special perioada zilei in care se efectueaza controlul.

In concluzie, controlul 100% lasa sa treaca in medie 15% din piesele defecte existente in lot.

N4 - controlul integral este Nestimulativ pentru executatnt.

Daca executantul unei operatii de prelucrare stie ca dupa aceasta urmeaza un control 100%, el da mai putina atentie acestei operatii deoarece daca va gresi, ii vor fi returnate piesele necorespunzatoare. Daca el stie, in plus, ca fiabilitatea controlului este redusa si circa 15% din defecte vor scapa controlului, el socoteste ca va avea mai putin de lucru, deoarece nu i se vor returna decat 85% din piesele necorespunzatoare.

In concluzie executantul nu este stimulat in realizarea unor produse de calitate.

Controlul prin esantionare

Datorita dezavantajelor controlului 100% dar si a cresterii volumului controlului in cazul unei productii de serie sau in productia de unicate a unor produse mari, cu grad mare de complexitate si rol functional important, s-a impus ca alternativa rationala din punct de vedere tehnic si economic, controlul statistic

Controlul statistic se realizeaz[ prin verificarea bucat[ cu bucat[ a unor e]antioane reprezentative prelevate, la anumite intervale de timp, dintr-un lot obinut dup[ o faz[ de prelucrare.

Se definesc urmatoarele notiuni cu care se opereaza in controlul statistic:

Unitate de produs - obiectul verificat calitativ.

Lot - cantitatea definita dintr-o marfa, fabricata in conditii presupus uniforme, din care trebuie extras un esantion spre a fi supus verificarii calitative. El este caracterizat prin numarul de unitati de produs prezente in lot, N (efectivul lotului).

Esantion - una sau mai multe unitati de produs prelevate aleatoriu dintr-un lot, destinate sa furnizeze o informatie asupra lotului si, eventual, sa serveasca drept baza pentru o decizie referitoare la lotul de produse sau la procesul care a generat lotul de produse respectiv. El este caracterizat prin numarul unitatilor de produs prezente in esantion, n (efectivul esantionului).

Defectiv - unitate de produs care prezinta unul sau mai multe defecte (sinonim; unitate de produs cu defecte).

Procedura, folosita pentru construirea unui esantion, poarta denumirea de esantionare

Pentru aplicarea controlului statistic se actioneaza conform unui plan de esantionare, prin care se stabilesc regulile de alcatuire a unuia sau mai multor esantioane, astfel incat prelevarea unitatilor de produs sa se faca aleatoriu, unitatile constitutive ale lotului avand sansde egale de a intra in componenta esantionului.

In functie de numarul esantioanelor prelevate esantionare poate fi:

- simpla: se preleveaza un singur esantion;

- dubla: se mai poate preleva si al doilea esantion in functie de informatia furnizata de primul;

- multipla: se pot preleva pana la sapte esantioane succesive.

In functie de marimea esantioanelor se poate face o esantionare:

- empirica: se stabileste arbitrar marimea esantioanelor;

- statistico-matematica.

2.Controlul proceselor de productie

2.1. Metode de control in raport cu desfasurarea procesului tehnologic

Metodele de control prezentate anterior (cele in raport cu fluxul de fabricatie) pot fi privite si luand ca baza un proces tehnologic sau principala operatie a procesului. Din acest punct de vedere se disting trei etape ale controlului, respectiv controlul inaintea, in timpul si la incheierea procesului

Controlul inaintea inceperii procesului tehnologic.

Aceasta etapa incepe practic printr-un examen critic al proiectului constructiei respective, in vederea eliminarii oricaror cauze care ar conduce la un posibil insucces.

In aceasta prima faza se vor trece in revista:

procedeele tehnologice preconizate a se aplica;

utilajele disponibile si performantele lor;

materialele folosite;

transportul si manevrarea pieselor si semifabricatelor;

tratamentele termice necesare si posibilitatile practice de aplicare;

forta de munca disponibila (efectiv, calificare);

controlul nedistructiv, etc.

Personalul tehnic implicat in aceasta faza a primei etape are calificare inalta (ingineri, maistri, specialisti - proiectanti, metalurgi, tehnologi etc.), toti fiind familiarizati cu problemele specifice procesului tehnologic care urmeaza a se aplica.

Intr-o a doua faza a acestei etape se trece la controlul calitatii materialeor folosite (materiale de baza, de adaos, auxiliare).

Controlul acestor categorii de materiale se efectueaza prin verificarea documentelor insotitoare (etichete, marcaje, certificate de calitate, etc.), a aspectului, gradului de curatenie, deteriorarilor pe timpul transportului etc.

Personalul implicat in aceasta faza are calificare medie si cuprinde personal tehnic de control si personal operator (maistri, muncitori).

In aceasta faza se mai urmaresc si alte obiective:

controlul masinilor-unelte si al instalatiilor speciale;

controlul dispozitivelor de lucru si al sculelor necesare;

controlul instrumentelor de masurare (starea, precizia, existenta documentelor care atesta verificarea metrologica etc.).

In faza a treia a acestei etape este inclusa verificarea calificarii fortei de munca.

Se trec in revista:

disponibilul fortei de munca si gradul ei de calificare (numar de muncitori, calificareaa acestora, existenta certificatelor de competenta pentru cei care executa lucrari speciale). Daca lucrarea se executa sub supravegherea unui organism de supraveghere independent (de exemplu I.S.C.I.R. - Inspectia de Stat pentru Cazane si Instalatii de Ridicat), trebuie indeplinite cerintele acestui organism;

verificarea starii psihice si de sanatate a muncitorilor repartizati sa execute lucrari de mare importanta sau sa lucreze in conditii grele.

Activitatile descrise mai inainte pot fi corelate cu prevederile procedurii functie de sistem intitulata "Controlul proiectarii".

Controlul in timpul desfasurarii procesului tehnologic

Aceasta etapa incepe practic din momentul in care materiile prime si semifabricatele au fost aduse la locul de prelucrare.

Controlul se executa, in primul rand, de catre personalul operator, apoi de catre persoanele imediat urmatoare pe scara ierarhica: sef de echipa, maistru, inginer, eventual reprezentantul beneficiarului.

Se procedeaza la:

identificarea materialelor sau semifabricatelor;

verificarea starii in care se afla acestea si de modul in care s-au executat eventualele operatii de pregatire;

verificarea cantitatilor de materiale necesare desfasurarii procesului tehnologic in bune conditii;

supravegherea modului in care sunt reglate utilajele si a modului in care ele functioneaza;

verificarea periodica a capabilitatii masinilor-unelte si echipamentelor folosite;

executarea unor operatii intermediare de control impuse de specificul tehnologiei respective.

Activitatile descrise mai sus se pot regasi in cadrul procedurilor functie de sistem "controlul proceselor" si "tehnici statistice".

Controlul la incheierea procesului tehnologic

In aceasta etapa se ia decizia de acceptare/ respingere a produselor. Ea coincide cu controlul final.

In mod normal, aplicarea controlului preventiv (primele doua etape descrise), trebuie sa constituie o garantie suficienta pentru succesul lucrarii respective.

Totusi, numerosi factori care influenteaza procesele de prelucrare si abaterile imprevizibile de la disciplina tehnologica, conduc in mod inevitabil la neconformitati* mai mult sau mai putin grave.

Obiectivul acestei etape de control consta tocmai in depistarea acestor neconformitati. Ea include metode si tehnici de control distructive sau nedistructive, metode statistice etc.

2.2. Metode de control statistic

2.2.1. Controlul statistic pe flux de fabricatie

Controlul statistic pe flux de fabricatie are drept scop:

a)           verificarea calit[ii materiilor prime, materialelor, componentelor sau produselor aprovizionate @n vederea utiliz[rii @n procese de producie;

b)           verificarea desf[]ur[rii proceselor de fabricaie @n vederea meninerii acestora @n limite de funcionare prestabilite;

c)           verificarea calit[ii produselor finite.

Organizarea acestui control presupune rezolvarea urm[toarelor probleme:

stabilirea caracteristicilor de verificat;

stabilirea fazelor procesului de producie sau a locurilor de munc[ unde se fac m[sur[torile;

stabilirea metodelor ]i mijloacelor de m[surare;

stabilirea metodelor de @nregistrare ]i prelucrare a informaiilor;

stabilirea m[rimii e]antionului ]i a frecvenei prelev[rilor;

stabilirea metodelor de prelevare;

stabilirea parametrilor controlului.

Parametrii specifici controlului proceselor de producie:

Limitele de toleran[

- Tolerana inferioar[ (TI), reprezint[ nivelul minim admis al unei caracteristici;

- Tolerana superioar[ (TS), reprezint[ nivelul maxim admis al unei caracteristici;

C`mpul de toleran[ (T) reprezint[ zona cuprins[ @ntre cele dou[ limite de toleran[: T=TS-TI. Pentru o caracteristic[ cu valori ce evolueaz[ dup[ o distribuie normal[, .

Centrul c`mpului de toleran[ :

Limitele de control statistic

- Limita de control inferioar[ (LCI);

- Limita de control superioar[ (LCS).

Limitele de supraveghere

- Limita de supraveghere superioar[ (LSS);

- Limita de supraveghere inferioar[ (LCS).

Riscul

- Risc de genul I, notat _a , reprezint[ probabilitatea de a considera c[ procesul de producie nu se desf[]oar[ normal de]i, @n realitate, acesta funcioneaz[ corect. Astfel, @n cazul unui risc de genul I _a= 0,005, concluzia este c[ @n 5 cazuri din 1000 se obin valori ale parametrilor de control (medie, mod, median[, dispersie) @n afara limitelor de control cu toate c[ procesul de producie se desf[]oar[ normal ceea ce reprezint[ un semnal fals;

Risc de genul II, notat _b reprezint[ probabilitatea de a considera c[ procesul se desf[]oar[ normal cu toate c[ acesta este necorespunz[tor.

Parametrii regl[rii ]i preciziei

Reglarea procesului de producie este caracterizat[ de centrul de grupare estimat pe baza mediei (), medianei (M_e) sau modului (M_o) e]antionului. Se consider[ c[ utilajele sau procesele de producie sunt reglate atunci c`nd parametrii centrului de grupare coincid ca nivel cu m[rimea centrului c`mpului de toleran[.

Precizia este caracterizat[ de limitele efective @ntre care se situeaz[ valoarea caracteristicii m[surate. Acest parametru se estimeaz[ cu ajutorul abaterii medii p[tratice a populaiei totale s, a celei de sondaj s sau cu ajutorul amplitudinii variaiei w.

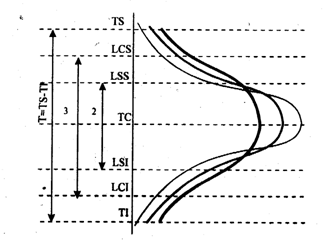
Pentru @ntregirea concluziilor se mai pot calcula: coeficientul de variaie (c_v), coeficientul de asimetrie (b

Figura 2. Limite utilizate @n controlul statistic al proceselor de producie

Relaiile utilizate pentru calculul acestor parametri sunt:

- media aritmetic[

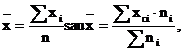@n care: (1)

x_i - nivelul caracteristicii la m[sur[toarea i;

n - num[r de m[sur[tori (de valori observate);

x_ci - valoarea central[ a intervalului i, @n cazul valorilor grupate pe clase;

n_i - num[rul valorilor m[surate care au nivelul cuprins @n intervalul i.

- mediana este valoarea central[ @ntr-o serie de date ordonat[ cresc[tor sau descresc[tor ]i se calculeaz[ cu una din relaiile:

- pentru un ]ir cu num[r par de valori:

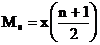(2)

- pentru un ]ir cu num[r impar de valori:

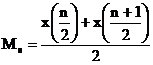(3)

- pentru serii de frecven[ grupate pe intervale, @n care:

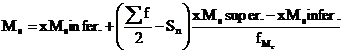(4)

- valoarea din ]ir cu num[rul de ordine

- valoarea din ]ir cu num[rul de ordine

- valoarea inferioar[ a intervalului median;

- valoarea superioar[ a intervalului median;

- num[rul total al unit[ilor statistice ale seriei;

S_n - suma frecvenelor intervalelor superioare intervalului median;

K - m[rimea intervalului median ;

- frecvena intervalului median.

- modul este valoarea caracteristicii c[reia @i corespunde cea mai mare frecven[ ]i a c[rui valoare se stabile]te @n mai multe moduri:

direct, conform definiiei, pentru serii obi]nuite;

prin calcul, pentru serii grupate pe intervale:

(5)

@n care:

- limita inferioar[ a intervalului @n care se situeaz[ modul;

D₁ - diferena dintre frecvena intervalului modal ]i frecvena intervalului inferior ca m[rime;

D₂ - diferena dintre frecvena intervalului modal ]i frecvena intervalului superior ca m[rime;

k - m[rimea intervalului modal.

Pentru repartiii de frecven[, apropiate de distribuia normal[ se poate folosi relaia:

abaterea medie p[tratic[ a valorilor din e]antion se calculeaz[ cu relaia:

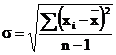(7)

- amplitudinea variaiei (R):

(8)

- coeficientul de variaie:

(9)

- coeficientul de asimetrie:

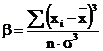(10)

#n funcie de valorile obinute pentru parametrii preciziei ]i regl[rii se poate @nt`lni una din urm[toarele situaii:

1) procesul de producie este stabil ca reglaj ]i precizie atunci c`nd centrul de grupare () corespunde cu centrul c`mpului de toleran[ (T_C), iar c`mpul de @mpr[]tiere este inclus @n c`mpul de toleran[ (fig.     a);

2) procesul de producie corespunde ca reglare dar nu corespunde ca precizie (c`mpul de @mpr[]tiere dep[]e]te c`mpul de toleran[ (fig. b);

3) procesul de producie corespunde ca precizie dar nu corespunde ca reglare (centrul de grupare este deplasat spre limitele de toleran[ (fig.     c ]i d);

4) procesul de producie este necorespunz[tor at`t ca precizie c`t ]i ca reglare (fig.     c ]i f). Prezint[ importan[ ]i dou[ cazuri speciale (g ]i h) pentru care procesul de producie este necorespunz[tor: @n cazul g utilaje cu precizie mare sunt folosite @n prelucr[ri cu cerine reduse fa[ de precizie; @n cazul h o mic[ dereglare a procesului duce la apariia rebuturilor. #n cazurile b, c, d, e, f se obin rebuturi.

Figura     St[ri posibile ale procesului de producie

Fazele controlului statistic al proceselor de producie:

Analiza premerg[toare introducerii controlului statistic

Elaborarea fi]elor de control

Elaborarea controlului

1. Analiza procesului @n vederea introducerii controlului statistic

Are drept scop:

a)           identificarea funciei de repartiie a nivelurilor caracteristicii controlate;

b)           verificarea stabilit[ii procesului tehnologic;

a)           Funcia de repartiie

Caracteristica de calitate analizat[ nu are tot timpul aceea]i valoare datorit[ variaiei unor factori obiectivi sau subiectivi. Pentru efectuarea controlului statistic trebuie cunoscut[ distribuia teoretic[ a frecvenei valorilor caracteristicii. De obicei, pentru caracteristicile m[surabile, aceasta este o distribuie normal[ (care trebuie verificat[), iar pentru cele atributive o distribuie Poisson. Pentru verificarea normalit[ii distribuiei se pot utiliza mai multe metode, mai uzual[ fiind metoda criteriului c

Se utilizeaz[ relaia:

, (11)

@n care:

N - num[rul total al valorilor ]irului statistic (N50);

n - num[rul valorilor dintr-o clas[ (n5);

k - num[rul claselor ();

p_i =f(z_i)- f(z_i-1), unde f(z) reprezint[ valorile funciei normate Laplace pentru care f(-z) =f(z)

(12)

Valoarea calculat[ c_c se compar[ cu valoarea c _a,f din tabele.

Dac[c_c >c _a,f se respinge ipoteza normalit[ii repartiiei empirice.

b) Verificarea stabilitatii procesului tehnologic

Controlul statistic nu poate fi utilizat @n cazul proceselor de producie care sunt instabile ca precizie sau reglaj. Dereglarea funcion[rii utilajelor sau a desf[]ur[rii proceselor de producie sunt determinate de mai muli factori care pot fi @mp[rii @n dou[ grupe:

- factori sistematici, a c[ror aciune se manifest[ @n acela]i mod ]i determin[ abateri @ntr-un singur sens. Ace]ti factori determin[ abaterea centrului de grupare de la centrul c`mpului de toleran[ sau @mpr[]tierea nivelurilor caracteristicilor @n afara c`mpului de toleran[. #ntre ace]ti factori putem meniona: calificarea operatorului, uzura sculelor, calitatea materiei prime, dereglarea ma]inii, etc. Aciunea factorilor sistematici este reflectat[ de anumite anomalii @n fi]ele de control: puncte @n afara limitelor, puncte situate numai @n apropierea unei limite, etc.

- factori @nt`mpl[tori, care determin[ abateri @n ambele sensuri, @n multe situaii aciunea lor anihil`ndu-se reciproc: neomogenitatea materiei prime, variaia tensiunii curentului de alimentare, neatenia operatorului, etc.

Un proces de producie este stabil dac[ abaterile sunt determinate numai de factori @nt`mpl[tori. Stabilitatea procesului de producie sau a utilajului sub aspectul regl[rii este @n general u]or de realizat prin intervenia muncitorului, care prin operaii specifice intervine aduc`nd centrul de grupare al valorilor caracteristicii la nivelul centrului c`mpului de toleran[.

Pentru a aprecia stabilitatea ca precizie se determin[ probabilitatea de a realiza rebuturi numit[ ]i fraciunea defect[ probabil[. Aceasta reprezint[ probabilitatea ca valorile caracteristicii s[ cad[ @n afara c`mpului de toleran[, respectiv:

p = p(x<TI; x>TS) = 1 - p(TIxTS)

Dac[ avem @n vedere funcia de repartiie a caracteristicii x, respectiv F(x), rezult[:

p = 1 - [F(TS) - F(TI)], (13)

sau, @n cazul repartiiei normale:

p = 1 - [f(z_s) - f(z_i (14)

@n care:

(15)

Dac[ centrul c`mpului de toleran[ coincide cu centrul c`mpului de @mpr[]tiere (caz frecvent @nt`lnit), rezult[:

z_s = z_i = z (16)

unde

(17)

Fraciunea defect[ devine: p = 1 - 2f(z). (18)

Se consider[ c[ un proces este controlabil statistic dac[ 0,001p0,02 Pentru cazurile cu p < 0,001 procesele au o precizie foarte ridicat[, care nu este neap[rat cerut[ de beneficiarii produselor.

Practic, pentru a verifica stabilitatea procesului de producie se procedeaz[ astfel:

- se stabile]te m[rimea e]antionului care va sta la baza fundament[rii concluziilor;

- se preleveaz[ e]antionul, se fac m[sur[tori ]i se calculeaz[:

(19)

- se stabile]te, cu ajutorul tabelelor statistice, probabilitatea p(z).

Ca m[sur[ a preciziei procesului se utilizeaz[ un indicator special numit capabilitatea procesului care reflect[ capacitatea acestuia de a realiza produse corespunz[toare ca centru de grupare ]i @mpr[]tiere. Nivelul acestui indicator se calculeaz[ ca raport @ntre num[rul abaterilor medii acceptate ]i nivelul c`mpului de toleran[:

, (20)

@n care:

d - num[rul abaterilor medii acceptate.

Se recomand[ pentru d valoarea 6 ceea ce @nseamn[:

. (21)

De asemenea se consider[ c[ ar trebui s[ avem 0,6 < C_p < 0,8, adic[ 7,5s < T < 10s ceea ce @nseamn[ abateri de la centrul de grupare cuprinse @ntre (3,75s; 5s)

2. Elaborarea fi]elor de control statistic

Fi]a de control, numit[ ]i carte de control, reflect[ starea procesului de producie sau a unui utilaj @n timpul funcion[rii active. Aceasta se poate prezenta sub mai multe forme:

- sub forma unui tabel @n care muncitorul care lucreaz[ la un utilaj, sau un controlor specializat, consemneaz[ rezultatele m[sur[torilor efectuate asupra unei caracteristici a produselor rezultate ]i, @n baza unor prelucr[ri sumare, adopt[ una din deciziile:

C - continuarea activit[ii;

R - @ntreruperea activit[ii @n vederea regl[rii utilajului (procesului);

O - oprirea utilajului @n vederea efectu[rii unor intervenii de complexitate sporit[.

- un sistem de afi]are automat[ (imprimant[, ecran) a informaiilor privind rezultatele m[sur[torilor cu precizia deciziei recomandate;

- un sistem automat de reglare a procesului @n funcie de anumii parametri de comand[.

Pe o astfel de fi][ se reprezint[ principalii parametrii ai procesului ]i ai caracteristicii de calitate.

Efectuarea controlului

Dup[ stabilirea parametrilor controlului statistic se aleg mijloacele de m[surare, programul de lucru al controlorilor, modalit[ile de @nregistrare a datelor ]i una dintre metodele de m[surare adecvate tipului caracteristicii ce face obiectul controlului statistic:

- metode bazate pe m[surarea caracteristicilor

- metode bazate pe atribute

- metode bazate pe num[rul de defecte

#n funcie de metoda utilizat[ ]i de rezultatele obinute se adopt[ decizia de continuare sau oprire a activit[ii @n vederea regl[rii sau repar[rii utilajului.

Controlul statistic al proceselor de producie prin m[surare

#n cazul caracteristicilor m[surabile se consider[ ipoteza repartiiei lor dup[ legea normal[ sau o lege apropiat[ de aceasta cu media m ]i dispersia s . Pe baza rezultatelor m[sur[torilor se calculeaz[ parametrii regl[rii ]i preciziei prin combinarea c[rora rezult[ una din urm[toarele metode de control:

Metoda mediei aritmetice ]i abaterii medii p[tratice

Metoda mediei aritmetice ]i amplitudinii @mpr[]tierii

Metoda medianei ]i amplitudinii @mpr[]tierii

Controlul pe baz[ de medie aritmetic[ ]i abatere medie p[tratic[

Aceast[ metod[ de control necesit[ un volum mai mare de calcule dar este mult mai eficient[ dec`t celelalte metode. Se recomand[ a se aplica atunci c`nd produsul este scump ]i important din punct de vedere funcional sau precizia prescris[ este mare, deci rezultatele controlului trebuie s[ fie c`t mai precise.

La utilizarea metodei putem @nt`lni trei situaii:

A.           se cunoa]te abaterea medie p[tratic[ a populaiei totale (s

B.           se cunosc abaterile medii p[tratice (s_i) pentru mai multe e]antioane;

C.           se cunosc amplitudinile @mpr[]tierii pentru mai multe e]antioane.

A. Se cunoa]te s

Limitele de control pentru media aritmetic[ se calculeaz[ cu ajutorul relaiilor urm[toare:

(22)

z_a - valoarea variabilei normale z pentru riscul acceptat a

#n mod similar se stabilesc ]i limitele de supraveghere cu singura deosebire c[ se lucreaz[ cu alte valori pentru z_a valori mai mici).

De regul[, valorile utilizate pentru z_a sunt

z_a pentru intervalul 1s, cu un risc de 32%
(a

z_a pentru intervalul 2s, cu un risc de 5%
(a

z_a=3,09 pentru intervalul 3s, cu un risc de 0,2%
(a

#n mod curent se lucreaz[ cu z_a=1,96 pentru limitele de supraveghere ]i cu z_a=3,09 pentru limitele de control.

Pentru abaterea medie p[tratic[ limita de control se calculeaz[ cu relaia:

, (23)

unde:

n-1- num[rul gradelor de libertate

- valoarea funciei .

Valoarea parametrului s este cea prev[zut[ @n specificaii sau determinat[ pe baza mai multor e]antioane de volum mare (n>5). #n ultima situaie se are @n vedere faptul c[ pentru mai multe e]antioane provenite din aceea]i populaie total[ avem:

- media repartiiei mediilor e]antioanelor este egal[ cu media populaiei totale;

(24)

- dispersia repartiiei mediilor e]antioanelor este a n-a parte din dispersia general[:

(25)

Pentru centrul c`mpului de toleran[ se adopt[ valoarea TC = m₀.

B. Se cunosc abaterile medii p[tratice ale mai multor e]antioane

#n acest caz se calculeaz[ mai @nt`i media abaterilor medii p[tratice cu una din relaiile:

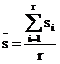, (26)

c`nd e]antioanele au volume egale (n);

, (27)

c`nd e]antioanele sunt de volum diferit;

r - num[rul e]antioanelor.

#n continuare se determin[ abaterea medie p[tratic[ cu relaia:

, (28)

Valorile parametrului b_n sunt calculate @n tabele statistice (STAS R 5880-72) (tabelul 1.).

Tabelul 1. Valorile coeficientului b_n

C. Se cunosc amplitudinile @mpr[]tierii mai multor e]antioane

Pentru utilizarea acestei metode se calculeaz[ mai @nt amplitudinea medie folosind una din relaiile:

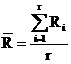, (29)

pentru e]antioane de acela]i volum n (e]antioane egale);

, (30)

pentru e]antioane de volum diferit.

Limitele de control ]i supraveghere se determin[ la fel, pe baza variabilei (s), calculat[ cu relaia:

, (31)

@n care a_n este media raportului dintre amplitudine ]i abaterea medie p[tratic[: (tabelul 2.).

Tabelul 2. Valorile coeficientilor a_n

Ultimele dou[ variante ale metodei se utilizeaz[ atunci c`nd procesul de producie nu permite cercetarea unui volum mare de produse pentru stabilirea valorii s aferent[ @ntregii populaii ]i c`nd specificaiile nu prev[d o anumit[ valoare pentru s

Exemplu: Prin prelucrarea unei bare de oel se obin repere cu o lungime de 200 mm. Abaterile acceptate sunt de

Rezult[:

TI = 200 - 1= 199 mm

TS = 200 + 1 = 201 mm

TC =

Pentru introducerea controlului statistic sunt prelevate la intervale egale de timp e]antioane de volum n = 5. Putem avea una din situaiile:

A. din specificaii se cunoa]te ]i se calculeaz[:

deoarece

B. Nu se cunoa]te s

Sunt extrase 5 e]antioane din populaia total[ pentru care se calculeaz[ Valorile m[surate pentru cinci e]antioane constituite aleator sunt date in tabelul nr.

Tabelul     Valori m[surate pentru cinci e]antioane