ELEMENTE DE MECANICA ANALITICA

COORDONATE GENERALIZATE

Punctul material reprezinta una din notiunile fundamentale ale mecanicii. Pozitia unui punct material in spatiu este determinata de raza sa vectoare ale carei componente coincid cu coordonatele carteziene x, y, z. Derivata lui in raport cu timpul t, este viteza, iar derivata de ordinul doi este acceleratia punctului material.

Pentru determinarea pozitiei unui sistem de N puncte materiale sunt necesare N raze vectoare, adica 3N coordonate. In general, numarul de marimi independente necesare pentru a determina in mod univoc pozitia unui sistem se numeste numar de grade de libertate ale sistemului. In cazul celor N puncte materiale, numarul gradelor de libertate este 3N. Aceste marimi nu sunt obligatoriu coordonatele carteziene ale punctului; in functie de conditiile problemei, poate fi mai comoda alegerea unui alt sistem de coordonate.

Fie s marimi q₁, q₂, .q_s ce caracterizeaza complet pozitia unui sistem (cu s grade de libertate) pe care le vom numi coordonate generalizate iar derivatele lor, in raport cu timpul vitezele generalizate. Nu este suficient sa cunoastem coordonatele generalizate pentru a determina "starea mecanica" a unui sistem la un moment dat. Pentru valorile date ale coordonatelor, un sistem poate sa aiba viteze arbitrare si in functie de valorile acestora pozitia sistemului poate fi diferita intr-un moment t ulterior. Experienta arata ca cunoasterea simultana a coordonatelor generalizate si a vitezelor generalizate determina complet starea unui sistem. Din punct de vedere matematic, aceasta semnifica faptul ca cunoasterea coordonatelor si a vitezelor la momentul t defineste in mod univoc valoarea acceleratiilor in acel moment.

2 PRINCIPIUL MINIMEI ACTIUNI

Principiul minimei actiuni (sau principiul lui Hamilton) conduce la o formula generala (alternativa) complet echivalenta cu legile de miscare ale sistemelor mecanice formulate de Newton.

Fiecare sistem mecanic poate fi descris de functia

sau pe scurt numita functia Lagrange. Presupunem ca in momentele t=t₁ si t=t₂ un sistem este caracterizat de ansamblurile de coordonate q⁽¹⁾, respectiv q⁽²⁾. Intre aceste pozitii, sistemul se misca astfel incat integrala

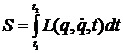(1)

sa aiba valoarea minima posibila. Integrala (1) se numeste actiune.

Functia Lagrange contine numai marimile q si , nu si derivatele de ordin superior. In acest mod rezulta ca starea mecanica a sistemului este complet definita de coordonatele si vitezele sale.

In cele ce urmeaza trebuie sa determinam ecuatiile diferentiale care determina minimul integralei (1). Pentru simplificare admitem ca sistemul are un singur grad de libertate q(t). Daca q(t) este functia pentru care S are un minim, inseamna ca S creste atunci cand q(t) este inlocuita prin

, (2)

unde dq(t) este o functie definita pe intregul interval de la t₁ la t₂, numita variatia q(t). Deoarece pentru t=t₁ si t=t₂ toate functiile de forma (2) trebuie sa aiba valorile q⁽¹⁾ si q⁽²⁾, rezulta ca

dq(t₁) = dq(t₂) = 0 (3)

Variatia actiunii S datorita modificarii lui q in q+dq este data de diferenta

.

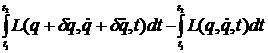Dezvoltarea in serie a acestei diferente dupa puterile lui dq si in expresia lui L incepe cu termenii de ordinul intai. Conditia necesara de extrem a lui S este ca toti acesti termeni sa se anuleze.

Principiul minimei actiuni se poate scrie

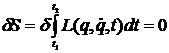(4)

adica

.

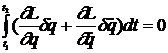Cum , integand prin parti al doilea termen se obtine

.

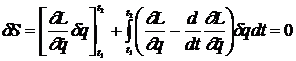Conform relatiei (3), primul termen din ecuatia de mai sus este zero. Deoarece dS=0 pentru toate valorile dq, rezulta ca

.

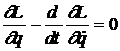Daca sistemul are s grade de libertate, cele s functii diferite q_i(t) variaza independent si se obtin s ecuatii de forma

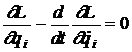. (5)

Ecuatiile (5) sunt ecuatiile diferentiale cautate si se numesc ecuatiile lui Lagrange. Daca se cunoaste functia Lagrange a unui sistem mecanic, relatiile (5) stabilesc legatura dintre acceleratii, viteze si coordonate, adica constituie ecuatiile de miscare ale sistemului.

Din punct de vedere matematic, ecuatiile (5) formeaza un sistem de s ecuatii diferentiale de ordiul al doilea cu s functii necunoscute q_i(t). Solutia generala a acestui sistem contine 2s constante arbitrare. Pentru determinarea acestora si, deci, pentru descrierea completa a sistemului mecanic este necesara cunoasterea conditiilor initiale ce caracterizeaza starea sistemului la un moment dat, de exemplu, valorile initiale ale coordonatelor si ale vitezelor.

FUNCTIA LAGRANGE PENTRU UN PUNCT MATERIAL

LIBER

Pentru studiul fenomenelor mecanice trebuie sa alegem un sistem de referinta. In raport cu un sistem de referinta oarecare, spatiul este neomogen si anizotrop. Aceasta inseamna ca daca un corp nu interactioneaza cu alte corpuri, diferitele sale pozitii in spatiu sau diferitele orientari nu sunt echivalente din punct de vedere mecanic. Din punct de vedere al timpului, acesta este neuniform.

Descrierea fenomenelor mecanice intr-un sistem cu astfel de proprietati ale spatiului si ale timpului devine foarte complicata. Astfel, pentru a determina forma functiei Lagrange vom considera un caz simplu: miscarea libera a unui punct material intr-un sistem de referinta galileian. Sistemul pentru care spatiul este omogen si izotrop iar timpul este uniform se numeste galileian. Intr-un astfel de sistem, un corp liber aflat in repaus la un anumit moment de timp ramane in repaus un timp nelimitat.

Uniformitatea spatiului si a timpului semnifica faptul ca functia Lagrange nu poate sa contina explicit nici raza vectoare a punctului material si nici timpul t. Altfel spus, functia Lagrange ramane o functie numai de viteza v. Insa, datorita izotropiei spatiului, L nu poate sa depinda de vectorul , ci numai de valoarea sa absoluta.

Deci,

. (6)

Pentru explicitarea acestei dependente vom utiliza principiul relativitatii al lui Galilei. Daca un sistem de referinta S se deplaseaza fata de un alt sistem S' cu viteza infinitezimala , atunci , unde si reprezinta vitezele aceluiasi punct in raport cu cele doua sisteme de referinta inertiale.

Deoarece ecuatiile de miscare trebuie sa aiba aceeasi forma in toate sistemele de referinta inertiale, prin trecerea de la S la S' functia Lagrange L(v²) se transforma intr-o functie L' care, daca difera de L(v²), atunci nu poate sa difere decat prin derivata totala a unei functii de coordonate si de timp.

Pentru a demonstra afirmatia de mai sus sa consideram doua functii si astfel incat

.

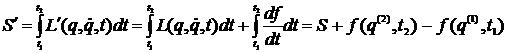Se observa ca cele doua actiuni difera printr-un termen care dispare atunci cand se calculeaza variatia actiunii (conform relatiei 3). Conditia coincide cu conditia si forma ecuatiilor de miscare ramane neschimbata. Folosind relatia Galilei dintre vitezele punctului material in cele doua sisteme de referinta inertiale, putem scrie

.

Dezvoltand aceasta expresie in serie in raport cu e si neglijand termenii de ordin superior, rezulta ca

.

Al doilea termen din membrul drept va fi o derivata totala in raport cu timpul a unei functii de coordonate si de timp daca ar fi o functie liniara in viteza , adica

L=av²,

unde a este o constanta.

Cum functia Lagrange satisface principiul relativitatii al lui Galilei in cazul unei transformari infinitezimale a vitezei, rezulta ca functia Lagrange este invarianta si in cazul unei viteze finite a sistemului de referinta S in raport cu S'. Astfel,

,

adica

.

In membrul drept, al doilea termen fiind o derivata totala a unei functii de coordonate si timp, poate fi omis.

Alegand constanta a=m/2, rezulta ca functia Lagrange pentru un punct material liber este de forma

. (7)

unde m este masa punctului material.

Deoarece functia Lagrange este o functie aditiva, pentru un sistem de puncte materiale se poate scrie

. (8)

FUNCTIA LAGRANGE PENTRU UN SISTEM DE PUNCTE

MATERIALE

Sa consideram un sistem de puncte materiale care interactioneaza intre ele si este izolat de mediul exterior; un astfel de sistem se numeste inchis. Interactia dintre punctele materiale ale sistemului se poate descrie cu ajutorul functiei Lagrange valabila pentru punctele materiale libere si a unei functii de coordonate (dependenta de caracterul interactiei din sistem). Notand aceasta functie cu -U, se poate scrie

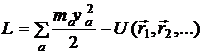, (9)

unde este raza vectoare a punctului a. Relatia (9) reprezinta forma generala a functiei Lagrange pentru un sistem inchis. Suma este energia cinetica iar U este energia potentiala a sistemului.

Faptul ca energia potentiala depinde numai de distributia punctelor materiale din sistem la un moment dat inseamna ca schimbarea pozitiei unuia dintre puncte se reflecta instantaneu asupra tuturor celorlalte: se poate spune ca interactia se propaga instantaneu. Acest caracter al interactiei corespunde mecanicii clasice; el decurge direct din postulatele fundamentale ale acesteia - existenta unui timp absolut si valabilitatea relativitatii galileiene.

Cunoscandu-se functia Lagrange, se pot scrie ecuatiile de miscare

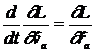(10)

adica, prin introducerea relatiei (9) in (10) se obtine

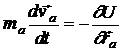. (11)

Sub forma (11) ecuatiile de miscare sunt cunoscute ca ecuatiile lui Newton si constituie baza mecanicii unui sistem de particule aflate in interactie. Vectorul

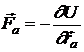(12)

se numeste forta care actioneaza asupra punctului a din sistem. La fel ca si energia potentiala, forta depinde numai de coordonatele particulelor si nu de vitezele lor.

Energia potentiala este o marime definita pana la o constanta arbitrara, dar acest lucru nu modifica ecuatiile de miscare. Modalitatea fireasca de a alege aceasta constanta este de a presupune ca energia tinde la zero atunci cand distanta dintre particule creste.

5 LEGI DE CONSERVARE

A. Energia

Atunci cand un sistem mecanic este in miscare, cele 2s marimi q si (i=1,2,s) care determina starea sa variaza in timp. Exista totusi niste functii de aceste variabile care, in timpul miscarii, isi pastreaza o valoare constanta. Aceste functii se numesc integrale prime ale miscarii.

In cazul unui sistem mecanic inchis cu s grade de libertate numarul integralelor prime independente este 2s-1. Se poate arata acest lucru prin cateva consideratii simple. Solutia generala a ecuatiilor de miscare contine 2s constante arbitrare. Deoarece ecuatiile de miscare ale unui sistem inchis nu contin in mod explicit timpul, se poate alege orice origine a timpului si una dintre constantele arbitrare care apare in solutia ecuatiilor de miscare se poate alege intotdeauna sub forma unei constante aditive parametrului timp, t_o. Eliminand t+t_o din cele 2s functii

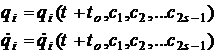
se pot exprima cele 2s-1 constante arbitrare c₁,c₂,c_2s-1 sub forma unor functii de q si , care sunt tocmai integralele prime ale miscarii.

Totusi, nu toate integralele prime au in mecanica roluri de aceeasi importanta. Printre ele sunt unele ale caror valori constante sunt legate de proprietatile fundamentale ale spatiului si timpului, adica uniformitatea si izotropia acestora. Toate aceste marimi, care sunt conservative, au o proprietate generala importanta: ele sunt aditive, adica valorile lor pentru un sistem format din particule intre care se neglijeaza interactia sunt egale cu suma valorilor corespunzatoare particulelor individuale. Proprietatea de aditivitate confera marimilor corespunzatoare un rol foarte important din punct de vedere mecanic. Sa presupunem ca doua corpuri interactioneaza intr-un anumit interval de timp. Dar inainte ca si dupa interactie fiecare dintre integralele prime (aditive) ale sistemului este egala cu suma valorilor lor corespunzatoare celor doua corpuri separate. Deci, legile de conservare ale acestor marimi permit cunoasterea starii corpurilor dupa interactie daca este cunoscuta starea acestora inainte de interactie.

Sa incepem cu legea de conservare ce deriva din proprietatea de uniformitate a timpului. Datorita acestei proprietati functia Lagrange a unui sistem inchis nu depinde in mod explicit de timp. Prin urmare, derivata totala a acestei functii in raport cu timpul se poate scrie

.

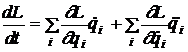Daca L ar fi fost o functie explicita de timp, in membrul drept al relatiei de mai sus ar fi trebuit sa adaugam termenul L t . Inlocuind derivatele L q_i prin valorile lor 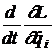din ecuatiile lui Lagrange, se obtine

sau,

.

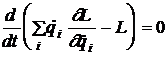Rezulta ca marimea

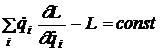(13)

ramane constanta in timpul miscarii mecanice a sistemului inchis. Ea constituie una dintre integralele prime ale miscarii si se numeste energia sistemului.

Proprietatea de aditivitate a energiei rezulta imediat din aditivitatea functiei Lagrange.

Legea conservarii energiei nu este valabila numai pentru sisteme inchise ci si pentru sistemele care se afla intr-un camp exterior constant (care nu depinde de timp); de fapt, singura proprietate a functiei Lagrange de a nu depinde explicit de timp folosita in rationamentul anterior ramane valabila si in acest caz.

Sistemele mecanice in care energia se conserva se numesc conservative.

Asa cum am vazut in paragraful 4, functia Lagrange pentru un sistem inchis (sau aflat in camp constant) este de forma

(14)

unde T este o functie de patratul vitezei. Aplicand teorema Euler pentru functii omogene obtinem

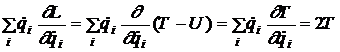. (15)

Folosind relatia (15), relatia (13) devine

.

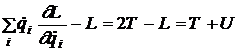Deci, energia sistemului este de forma

(16)

sau, in coordonate carteziene

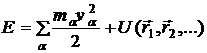. (17)

Astfel, energia sistemului se poate scrie ca o suma de doi termeni: energia cinetica ce depinde de viteze si energia potentiala ce depinde numai de coordonatele particulelor.

B. Impulsul

Proprietatea de omogenitate a spatiului conduce la o alta lege de conservare.

Datorita omogenitatii spatiului, proprietatile mecanice ale unui sistem inchis nu se modifica la o deplasare paralela a intregului sistem.

Sa consideram o deplasare infinit mica si sa impunem conditia ca functia Lagrange sa nu se modifice in urma acestei transformari. Prin deplasare paralela intelegem o transformare prin care toate punctele sistemului se deplaseaza cu acelasi segment; altfel spus, razele lor vectoare se modifica conform relatiei

. (18)

Variatia functiei Lagrange la o transformare a coordonatelor conform relatiei (18) este

,

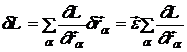suma fiind efectuata dupa toate particulele din sistem. Deoarece este arbitrar, conditia dL=0 este echivalenta cu

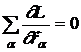
sau, folosind ecuatiile Lagrange,

.

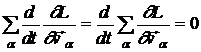Ajungem astfel la concluzia ca intr-un sistem mecanic inchis marimea vectoriala

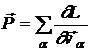(19)

numita impulsul sistemului ramane neschimbata in timpul miscarii.

Cum

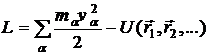
rezulta ca impulsul se exprima in functie de vitezele particulelor din sistem sub forma

. (20)

Proprietatea de aditivitate a impulsului este evidenta. In plus, spre deosebire de cazul energiei, impulsul sistemului este egal cu suma impulsurilor particulelor din sistem chiar daca interactiile dintre particule nu sunt neglijabile.

Legea de conservare a impulsului nu este valabila pentru toate cele trei componente ale impulsului decat in absenta unui camp extern. In acelasi timp, unele componente ale impulsului se pot conserva individual si intr-un camp extern daca energia potentiala nu depinde de una dintre coordonatele carteziene. La o translatie de-a lungul axei ce corespunde acestei coordonate proprietatile mecanice ale sistemului nu se schimba si proiectia impulsului pe aceasta axa se va conserva. Astfel, intr-un camp uniform de-a lungul axei z, componentele impulsului pe axele x si y se vor conserva.

Egalitatea 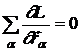are si un sens fizic deoarece derivata 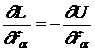reprezinta forta ce actioneaza asupra particulei a. Egalitatea semnifica faptul ca suma fortelor care actioneaza asupra tuturor particulelor sistemului este egala cu zero:

In particular, in cazul unui sistem alcatuit numai din doua puncte materiale, , adica forta exercitata de prima particula asupra celei de-a doua este egala dar opusa fortei exercitate de cea de-a doua particula asupra primei. Aceasta afirmatie este cunoscuta sub numele de legea egalitatii actiunii cu reactiunea.

Daca miscarea este descrisa cu ajutorul coordonatelor generalizate q_i, derivatele functiei Lagrange in raport cu vitezele generalizate,

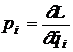(21)

se numesc impulsuri generalizate, iar derivatele functiei Lagrange in raport cu coordonatele generalizate

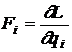(22)

se numesc forte generalizate. Ecuatiile Lagrange se mai pot scrie sub forma

(23)

6 ECUATIILE HAMILTON

Formularea legilor mecanicii cu ajutorul functiei Lagrange (si a ecuatiilor Lagrange) presupune cunoasterea coordonatelor generalizate si a vitezelor generalizate ale sistemului. Descrierea starii unui sistem cu ajutorul coordonatelor si a impulsurilor generalizate prezinta un numar mare de avantaje in studiul problemelor de mecanica. Dar trebuie sa cautam ecuatiile de miscare potrivite acestei formulari. Se poate trece de la un set de variabile independente la altul cu ajutorul unei transformari cunoscute in matematica sub denumirea de transformarea lui Legendre.

Diferentiala totala a functiei Lagrange de coordonate si viteze este

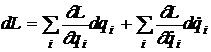. (24)

Cum 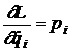si 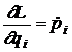, relatia (24) se mai poate scrie

. (25)

Ultimul termen din membrul drept al relatiei de mai sus este

.

iar relatia (25) devine

.

Sau,

.

Functia de sub semnul diferentiala reprezinta energia sistemului. Exprimata in functie de coordonate si de impulsuri, ea se numeste functia lui Hamilton:

(26)

Din egalitatea

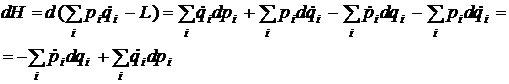
rezulta ecuatiile

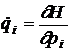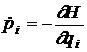, . (27)

Relatiile (27) reprezinta ecuatiile de miscare cautate si se numesc ecuatiile Hamilton. Ele constituie un sistem de 2s ecuatii diferentiale de ordinul intai cu 2s functii necunoscute p(t) si q(t) care inlocuiesc cele s ecuatii de ordinul al doilea obtinute prin metoda lui Lagrange. Datorita simplitatii si a simetriei lor, aceste ecuatii se numesc canonice.

Derivata totala in raport cu timpul a functiei Hamilton este

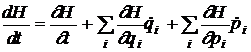
Introducand ecuatiile Hamilton in relatia de mai sus se obtine

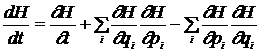
T .

In particular, daca functia Hamilton nu depinde explicit de timp, rezulta ca dH/dt=0 si regasim legea de conservare a energiei.

7 PARANTEZELE POISSON

Fie f(p,q,t) o functie de coordonatele generalizate, de impulsuri si de timp. Derivata sa totala in raport cu timpul este

.

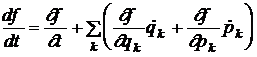Inlocuind si cu expresiile lor date de ecuatiile Hamilton (27) se obtine

unde

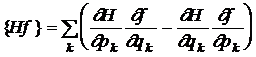(28)

reprezinta paranteza Poisson a lui H cu f.

Functiile de variabile dinamice care raman constante in timpul miscarii sistemului constituie, asa cum am vazut, integralele prime ale miscarii. Conditia ca functia f sa fie o integrala prima este

, ceea ce implica .

Daca integrala prima nu depinde explicit de timp, rezulta ca

adica paranteza Poisson a lui H cu f trebuie sa se anuleze.

In cele ce urmeaza vom enumera cateva dintre proprietatile parantezelor Poisson care se deduc din relatia lor de definitie:

= -

= 0, unde c este o constanta.

= +

= f₁ + f₂

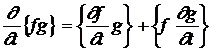
daca una dintre functiile f sau g coincide cu impulsul generalizat sau cu coordonata generalizata, atunci

,

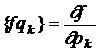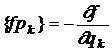
si

d_ik

intre parantezele Poisson ale functiilor f, g si h exista relatia

} = } = {h } = 0

numita identitatea lui Jacobi.

daca f si g sunt doua integrale prime, paranteza lor Poisson este si ea o integrala prima (teorema Poisson)

=const

8 TRANSFORMARI CANONICE

Alegerea coordonatelor generalizate nu este limitata de nici o conditie: se pot lua s marimi oarecare ce vor defini intr-un mod univoc pozitia sistemului in spatiu. Aspectul formal al ecuatiilor lui Lagrange nu depinde de aceasta alegere si, in acest sens, se poate spune ca ecuatiile lui Lagrange sunt invariabile in raport cu transformarea de la coordonatele

q₁,q₂, la alte marimi independente Q₁,Q₂,... Noile coordonate Q sunt functii de vechile coordonate q, admitand ca au fost alese in asa fel incat aceste relatii sa contina timpul in mod explicit, adica vom avea transformari de tipul

Q_i = Q_i(q, t) (29)

numite si transformari punctuale.

In afara ecuatiilor lui Lagrange, transformarea (29) lasa invarianta forma (27) a ecuatiilor lui Hamilton. In realitate, acestea din urma pot admite o clasa si mai larga de transformari. Acest lucru decurge in mod natural din faptul ca in metoda Hamilton impulsurile p joaca acelasi rol de variabile independente ca si coordonatele q. Se poate astfel largi definitia transformarilor in a a fel incat sa se inglobeze transformarea a 2s variabile independente p si q in noile variabile P si Q, cu formulele

Q_i = Q_i(p,q,t) P_i = P_i(p,q,t) . (30)

Sa stabilim acum conditiile pe care trebuie sa le satisfaca o transformare in asa fel incat ecuatiile de miscare in noile variabile P si Q sa aiba forma

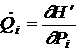, (31)

cu o noua functie a lui Hamilton H'(P,Q). Astfel de transformari se numesc canonice.

Ecuatiile Hamilton se pot obtine plecand de la principiul minimei actiuni scris sub forma

. (32)

Pentru ca si noile variabile P si Q sa satisfaca ecuatiile lui Hamilton, ele trebuie sa verifice principiul minimei actiuni:

. (33)

Prin urmare, expresiile de sub semnul integrala pot sa difere numai prin diferentiala totala a unei functii arbitrare F de coordonate, de impulsuri si de timp; diferenta dintre cele doua integrale (diferenta dintre valorile lui F la limitele de integrare) va fi o constanta a carei variatie va fi nula. In consecinta, vom avea

. (34)

Orice transformare canonica este caracterizata prin functia sa F numita functia generatoare a transformarii.

Scriind relatia (34) sub forma

(35)

se observa ca

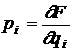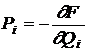, , (36)

functia generatoare presupunandu-se a fi o functie de vechile precum si de noile coordonate (ca si de timp): F = F(q,Q,t). Pentru o functie F data, relatiile (36) stabilesc legatura dintre vechile variabile (q,p) si noile variabile (Q,P), exprimandu-ne si noua functie Hamilton H'.

Sa notam faptul ca legatura dintre noua si vechea functie a lui Hamilton este intotdeauna univoca; diferenta H' - H este data de derivata partiala in raport cu timpul a functiei generatoare. In particular, daca functia generatoare nu depinde de timp, H' = H.

Extinderea clasei de transformari canonice priveaza notiunile de coordonate si impulsuri generalizate de o parte din sensul lor initial. Deoarece transformarile (30) leaga fiecare dintre marimile P si Q atat de coordonatele q cat si de impulsurile p, variabilele Q nu mai pot fi considerate ca niste coordonate pur spatiale. De exemplu, in transformarea cu functia generatoare F = Sq_iQ_i, Q_i=p_i , P_i =- q_i iar forma canonica a ecuatiilor nu se schimba ci revine doar la o interschimbare a denumirii coordonatelor si impulsurilor.

Tinand cont de aceste lucruri, in metoda lui Hamilton, variabilele p si q se mai numesc si marimi canonic conjugate.

Conditia ca doua marimi sa fie canonic conjugate se poate exprima cu ajutorul parantezelor Poisson. Este util sa demonstram teorema generala a invariantei parantezelor Poisson in raport cu transformarile canonice.

Fie _P,Q paranteza Poisson a marimilor f si g, unde derivata se face in raport cu variabilele p si q, si _p,q paranteza Poisson a acelorlasi marimi derivate in raport cu variabilele canonice P si Q. Exista atunci relatia

_p,q = _P,Q . (37)

Aceasta relatie se poate verifica printr-un calcul direct, utilizandu-se formulele transformarilor canonice. Astfel, obtinem

_p,q = 0 ; _p,q = 0 ; _p,q = d_ik

Relatiile (38) reprezinta conditiile pe care trebuie sa le satisfaca noile variabile astfel incat transformarea p,q P,Q sa fie canonica.

9 TEOREMA LUI LIOUVILLE

In interpretarea geometrica a fenomenelor mecanice se foloseste adesea notiunea de spatiu al fazelor: este un spatiu cu 2s dimensiuni pe ale caror axe sunt precizate s coordonate generalizate si s impulsuri generalizate ale sistemului mecanic.

Fiecare punct al acestui spatiu corespunde unei stari determinate a sistemului. Daca sistemul se misca, punctul din spatiul fazelor care-l reprezinta descrie o linie corespunzatoare traiectoriei in spatiul fazelor.

Vom considera produsul diferentialelor

dG = dq₁..dq_sdp₁dp_s

ca un 'element de volum' in spatiul fazelor. Integrala dG efectuata pe un domeniu oarecare D al acestui spatiu reprezinta volumul acelui domeniu.

Daca se considera fiecare punct al domeniului D ca stare initiala a sistemului la un moment initial t₀ si se urmareste deplasarea in timp de-a lungul traiectoriei sale pana la un moment final t, atunci totalitatea acestor puncte finale formeaza un domeniu D' care are un volum egal cu volumul domeniului D.

Pentru a demonstra aceasta teorema, cunoscuta sub numele de teorema lui Liouville, este suficient sa aratam ca ea este adevarata daca intervalul de timp dintre momentul initial si cel final este foarte mic, adica dt. Vom arata, deci, ca , unde G reprezinta volumul domeniului ocupat de punctele care, la momentul initial, se gasesc in D. Prin integrare, rezulta imediat ca G=const. Sa consideram un punct care, la momentul initial se gasea in D, si care avea coordonatele

p₁, p₂,.p_s,q₁,q₂,.q_s.

Dupa timpul dt, el va avea coordonatele p₁',p₂',.p_s',q₁',q₂',.q_s' date de relatiile

, (40)

in care si sunt date de ecuatiile canonice (27) si sunt functii de p si q. Volumul domeniului D ocupat de puncte la momentul initial este dat de integrala 2s-upla

. (41)

Volumul domeniului ocupat de puncte dupa timpul dt va fi dat de integrala

. (42)

Relatiile (40) se pot considera ca reprezentand o schimbare de variabile care permit trecerea de la variabilele p, q, la variabilele p', q'; prin efectuarea acestei schimbari in integrala (42), ea se reduce la o integrala asupra variabilelor p, q pe domeniul D'. Integrala va coincide cu (41), deci volumele domeniilor D si D' coincid, daca determinantul functional al transformarii (40) este egal cu unitatea. Expresia acestui determinant functional este

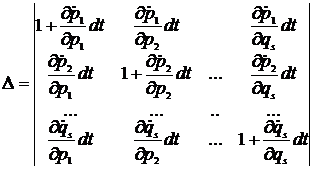
Din acest determinant se pastreaza numai termenii care il contin pe dt cel mult la puterea intai. In aproximatia ceruta, rezulta ca

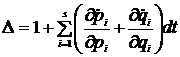
Inlocuind in relatia de mai sus pe si prin valorile lor date de ecuatiile canonice (27) obtinem

,

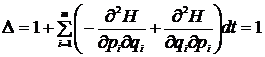ceea ce demonstreaza teorema lui Liouville. Se constanta ca valabilitatea acestei teoreme este o consecinta a formei canonice a ecuatiilor de miscare.