Miscari particulare ale solidului rigid

1 Miscarea de translatie a rigidului

Un rigid are miscare de translatie daca o dreapta oarecare a sa ramane paralela cu ea insasi in timpul miscarii .

Exemplu:scaunul unei roti de agrement (fig. 1)

Fig. 1

Determinarea pozitiei, vitezei si acceleratiei unui punct al rigidului.

Se considera sistemul de referinta mobil T(xOyz) avand axele paralele cu axele sistemului de referinta fix T₁(x₁O₁y₁z₁), (fig. 2).

M-punct oarecare avand miscare de translatie

O₁x_{1 ││} Ox

O₁y_{1 ││} Oy

O₁z_{1 ││} Oz

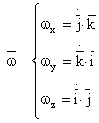(3)

Fig. 2

Versorii au directie constanta => = 0 , = 0 , = 0 => (4)

(5)

Deci: = (6)

Relatia (6) reprezinta legea distributiei de viteze in miscarea de translatie.

(7)

In aceste conditii relatia (7) devine:

(8)

Caracteristici ale miscarii de translatie :

toate punctele rigidului au acceasi viteza , viteza fiind un vector liber

toate punctele rigidului au acceasi acceleratie (egala cu acceleratia originii), acceleratia fiind un vector liber .

- translatia poate fi rectilinie sau curbilinie dupa cum traiectoriile punctelor sunt drepte sau curbe

(fig. 3) .

Fig. 3

Miscarea de rotatie a rigidului

Un rigid are miscare de rotatie daca doua puncte ale sale raman fixe in spatiu tot timpul miscarii .

Fie: O si O' : puncte fixe ale rigidului (fig. 4)

OO' - axa de rotatie

In O si O' - articulatii cilindrice

z = z₁

Fie M un punct oarecare in rigidul de rotatie

│O₁O│= constant

Determinarea vitezei punctului M :

deoarece O₁O= 0

Tinand cont ca:

(10)

Fig. 4

Relatia (10) reprezinta distributia de viteze in miscarea de rotatie.

Notam cu θ unghiul facut de Ox cu O₁x₁ si Oy cu O₁y_{1 .}

θ = θ(t) - reprezinta gradul de libertate in cazul rigidului cu axa fixa .

Tinand cont de relatiile (3):

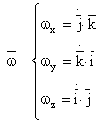
si exprimand versorii si in functie de θ avem :

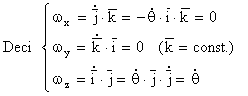
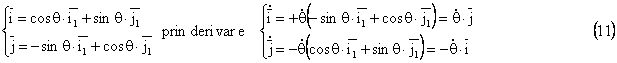
Relatia (13) arata ca vectorul ω are componenta numai pe axa Oz.

Tinand cont de relatiile (10) si (13) componentele vitezei sunt :

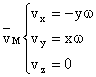
Determinarea acceleratiei punctului M :

Se pleaca de la relatia (25) de la pct. 9.3 :

= 0 pentru ca O - punct fix .

unde: (17)

Relatia (16) devine :

Relatia (18) reprezinta distributia de acceleratii din miscarea de rotatie a rigidului

Prin descompunerea relatiei (18) componentele acceleratiei sunt :

(vezi fig. 4)

Proprietati ale miscarii de rotatie :

- traiectoriile punctelor sunt cercuri perpendiculare pe axa de rotatie;

- vitezele punctelor sunt perpendiculare pe axa de rotatie, tangente la traiectorie;

v_M = ωR (21)

unde: R - raza traiectoriei (distanta de la punct la axa de rotatie).

- punctele situate pe drepte paralele cu ω au viteze si acceleratii egale (fig. 5) .

Fig. 5

Pe o dreapta perpendiculara pe axa de rotatie distributia de viteze si acceleratii este liniara

(fig. 6) .

Fig. 6

Singurele puncte de viteza si acceleratie zero apartin axei de rotatie .

Daca = constant - miscare de rotatie uniforma ω

= constant - miscare de rotatie uniform variata :- accelerata ε

- incetinita ω

ε

Observatie . Daca cunoastem n [rot/min] =>

Miscarea plan - paralela a rigidului

Un rigid are o miscare plan - paralela cand 3 puncte necoliniare ale sale raman tot timpul

miscarii continute in acelasi plan fix (fig. 7) .

Fig. 7

Fara a reduce generalitatea problemei se poate alege planul fix x₁O₁y (π₁)si planul mobil xOy (π) ,

(fig.8).

π - plan mobil solidar cu rigidul

π₁ - plan fix

π ║ π₁

Fie M - un punct oarecare al rigidului in miscare plan-paralela

Observatie . In general un rigid in miscare plan-paralela are 3 grade de libertate .

Pozitia punctului M:

Determinarea vitezei punctului M

Notam cu θ unghiul facut de Ox cu O₁x₁ si Oy cu O₁ y₁ ( fig. 8)_.

Reluand demonstratia de la miscarea de rotatie obtinem :

Dezvoltand relatia (26) si tinand cont de (27) si (28) obtinem componentele vitezei :

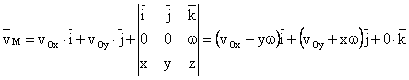
Se observa ca este situata intr-un plan perpendicular pe axa Oz (paralel deci cu xOy) .

Determinarea acceleratiei punctului M:

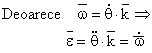
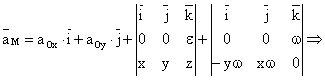
Dezvoltand relatia (30) si tinand cont de (31) obtinem:

Se observa ca este situat intr-un plan paralel cu xOy .