Regulatoare Automate Tehnician in Automatizari

Liceul de Metrologie ,,Traian Vuia" Director,

Proiect pentru obtinerea Certificatului de Calificare    Profesionala Nivel 3

Calificarea: Tehnician in Automatizari

Tema Proiectului: Regulatoare Automate

Argument

Pentru sustinerea examenului de Certificarea Competentelor Profesionale, in specialitatea Tehnician in Automatizari mi-am propus o tema care sa puna in evident competentele dobandite pe parcursul anilor de studiu, cat si a ma ajuta sa aprofundez cunostintele necesare sustinerii probei de specialitate in cadrul examenului de Bacalaureat.

Regulatorul automat este un aparat folosit pentru reglarea automata sau manuala a functionarii unui sisteam tehnic.Regulatorul automat este influentat de variatia marimii caracteristice pe care o regleaza si actioneaza asupra sisteamului fie printr-un releu electric, fie pe calea mecanica, pneumatic sau hidraulica, modificand functionarea sisteamului pana cand marimea de aer de care depinde regulatorul atinge valoarea dorit.

Lucrarea este structurata in 3 capitole care au urmatorul cuprins:

Capitolul I : Definirea regulatoarelor si clasificarea lor

Capitolul II : Legi de reglare si caracteristici

Capitulul III : Solutii constructive de implementare a legilor de reglare

Pe parcursul intocmirii lucrarii am avut de rezolvat urmatoarele problem:

documentarea, utilizand surse electronice si clasice;

selectarea informatiilor, oprindu-ma la cele mai relevante pentru tema aleasa;

organizarea proiectului

imbunatatirea abilitatilor de lucru cu calculatorul

Consider ca realizarea unui proiect ethnic mi-a permis structurarea cunostintelor dobandite, aprofundate si folosirea acestora in elaborarea unei lucrari complexe.

Regulatoare Automate

Capitolul I

Definirea regulatoarelor

Regulator

Aparat folosit pentru reglarea automata sau manuala a functionarii unui sisteam tehnic.Regulatorul automat este influentat de variatia marimii caracteristice pe care o regleaza si actioneaza asupra sisteamului fie printr-un releu electric, fie pe calea mecanica, pneumatic sau hidraulica, modificand functionarea sisteamului pana cand marimea de aer de care depinde regulatorul atinge valoarea dorit.Construcita regulatoarelor variaza dupa principiul pe care se bazeaza si dupa natura caracteristicilor pe care le regleaza:

a. Calitatea unui sistem tehnic de a se comporta conform unei reguli stabilite in prealabil

b. Aparat (eventual dispozitiv) al unui sistem de reglare automata, care primeste la intrare marimea de actionare a si transmite la iesire marimea de comanda c

c. Element al unui sistem de reglare automata caruia i se aplica la intrare marimea de actionare a si care produce la iesire marimea de comanda c, care este in functie de marimea de actionare a, de derivatele si integralele in raport cu timpul ale acesteia. In unele cazuri, prin regulator se intelege intreaga instalatie de automatizare.

Clasificarea regulatoarelor automate

a) RA electronice, pneumatice si hidraulice.

In functie de tipul marimilor fizice de la intrarea si iesirea RA, se deosebesc RA electronice, pneumatice si hidraulice.

La RA electronice marimile respective sunt marimi electrice (tensiuni sau curenti), iar in interiorul blocului RA prelucrarea acestor semnale - in conformitate cu legea de reglare adoptata - se realizeaza prin intermediul unor amplificatoare electronice si al unor rezistente si condensatoare.

La RA pneumatice marimile fizice de la intrarea si iesirea RA sunt presiuni, agentul purtator de informatii fiind aerul comprimat. Blocul RA contine amplificatoare pneumatice, rezistente si capacitati pneumatice ; constructia acestor RA se realizeaza prin intermediul elementelor cu membrane sau al celor cu burdufuri.

Agentul purtator de informatii la RA hidraulice este uleiul sub presiune, aceste regulatoare incluzand amplificatoare hidraulice (cu distributor sau cu tub cu jet), amortizoare hidraulice, siteme de parghii si resoarte.

Se folosesc si regulatoare mixate electron-pneumatice sau electron-hidraulice, in care intervin si elemente pneumatice (sau hidraulice), cuplate prin intermediul unor convertoare.

Avantaje

RA electronice au o serie aparte de avantaje : pot fi realizate in constructii miniaturizate (deci ocupa spatii mici, rezultand economii de spatiu in camerele de comanda, unde sunt instalate panourile cu regulatoare), semnalele electronice se transimit cu viteze foarte mari, iar cuplarea cu calculatoare electronice se face usor.

RA pneumatic e necesita o instalatie de prepararea si comprimarea aerului si conducte de legatura - ocupand spatii mai mari ca in cazul RA electronice - semnalele pneumatic se transmit mai lent decat cele electrice, iar cuplarea cu calculatoare electronice necesita convertoare suplimentare ; exista un avantaj deosebit de important al RA pneumatice in raport cu cele electronice si anume siguranta in medii cu pericol de incendiu sau de explozie (intrucat nu pot aparea scantei), ceea ce le recomanda pentru utilizare in aceste medii.

RA hidraulice ocupa spatii si mai mari decat cele pneumatic (intervin atat conducte de la statia de prepararea si comprimarea uleiului spre RA, cat si conducte de sens invers, pentru recuperarea uleiului), dar prezinta avantajul ca asigura obtinerea unor forte si cupluri mari, avand astfel prioritate in asemenea cazuri.

b) RA unificate si specializate

Clasificarea RA in unificate si specializate este strans legata de constructia regulatoarelor.

RA unificate functioneaza cu semnale unificate, respectiv la intrarea si iesirea subansamblelor si blocurilor componente sunt prevazute marimi de aceeasi natura fizica si cu aceeasi gama de variatie.

Astfel, la regulatoarele pneumatice semnalul unificat este reprezentat de o presiune variind in gama 0,2.1 bari (atmosfere suprapresiune), iar la regulatoarele electronice se folosesc ca semnale unificate : curentul continuu cu game de variatie de 2.10 mA sau 4.10 mA, tensiunea continua si minima din cadrul gamei de variatie este acelasi (5 la 1) la regulatoarele electronice si pneumatice, ceea ce permite conectarea lor (prin intermediul unor convertoare) in scheme mixte electrono-pneumatice.

Unificarea semnalelor prezinta mari avantaje. Astfel, diversele subansamble pot fi conectate in diferite moduri, intrucat au la intrari si iesiri aceeasi marime fizica si cu aceeasi gama de variatie, rezultand astfel proprietatea subansamblelor de a fi interschimbabile ; ca urmare, cu un numar relativ redus de subansamble poate fi realizata o mare varietate de scheme. Pe de alta parte, folosirea regulatoarelor unificate permite uniformizarea panourilor si simplifica exploatarea. In sfarsit, datorita flexibilitatii in conectarea subansamblelorm regulatoarele unificate nu sunt destinate numai unei anumite categorii de instalatii tehnologice automatizate - deci nu sunt specializate - ci pot fi folosite pentru reglarea diferitelor marimi din cadrul unei diversitati de instalatii tehnologice, avand astfel un caracter de generalitate (sau universalitate) a utilizarii.

Datorita acestor avantaje, regulatoarele unificate reprezinta principal directie in fabricarea regulatoarelor electronice si pneumatic.

Regulatoare specializate - dupa cum arata si denumirea lor - au o destinatie speciala (de exemplu: regulator de nivel pentru un anumit tip de cazan). Constructia lor este,de regula, adaptata la instalatia tehnologica automatizata si deci aria de utilizare este mai restransa. In present, indeosebi regulatoarele hidraulice mai sunt realizate ca regulatoare specializate, intrucat constructia lor este de mai multe ori in strans legata de constructia instalatiei tehnologice, de exemplu cum este cazul regulatoarelor de turatie ale turbinelor cu abur.

c) RA liniare si neliniare

La RA liniare dependenta in regim stationar (v.cap.2 din manualul "Echipamente electronice pentru automatizari" clasa a XI-a) dintre marimea de iesire si de intrare are un caracter liniar.

La RA neliniare dependenta mentionata este neliniara. Cele mai utilizate categorii de regulatoare neliniare sunt regulatoarele bipozitionale si tripozitionale, prezentate in paragraful 2, punctul b si in subcapitolul C.

d) RA continue si discrete

Marimile de intrare si iesire ale regulatoarelor continue sunt functii continue de timp, iar la RA discrete marimile respective au variatii discontinue (discrete), fiind esantionate.

Regulatoarele discrete functioneaza astfel cu impulsuri, iar acestea pot fi modulate (in amplitudine,durata etc.) sau codificate ; in cazul codificarii impulsurilor se obtin regulatoarele numerice, a caror importanta a crescut considerabil in ultimii ani, ca urmare a aparitiei microproceselor. Regulatoarele electronice numerice cu microprocesoare sunt prezentate in subcapitolul D.

e) RA pentru procese rapide si pentru procese lente

Unele procese - desfasurate in instalatiile tehnologice automatizate - au o evolutie rapida, iar altele au o evolutie lenta, primele fiind denumite procese rapid, iar celelalte procese lente.

In orice instalatie tehnologica din practica au loc intarzieri inerente in transmiterea semnalelor de la intrarea spre iesirea instalatiei, intrucat este evident necesar un anumit timp pentru propagarea spre iesirea a efectelor variatiei semnalului de la intrare ; valorile acestor timpi de propagare caracterizeaza procesele tehnologice ca rapide sau lente.

Daca s-ar presupune ca la o schimbare brusca a valorii marimii de intrare a instalatiei tehnologice (schimbarea brusca de la valoare anterioara constanta la o alta valoare constanta este denumita variatie treapta sau semnal treapta - v. cap 2 din manualui "Echipamente electronice pentru automatizari", clasa a XI-a) marimea de iesire variaza exponential,atunci timpul de propagare mentionat mai inainte poate fi caracterizat de constanta de timp a exponentialei respective ; daca nu la un semnal de intrare de tip treapta variatia marimii de iesire (denumita si "raspunsul" instalatiei tehnologice) reprezinta o suma de exponentiale - cum se intampla in multe cazuri din practica - atunci timpul de propagare poate fi definit prin intermediul constantelor de timp ale acestor exponential.

Din punct de vedere cantitativ se considera procese rapide cele caracterizate de constante de timp ale caror valori nu depasesc 10 secunde, procese lente fiind cele mai constant de timp mai mari, care pot ajunge la zeci de minute.

In practica, procesele rapide sunt cele care se desfasoara in masinile si actionarile electrice (motoare de current continuu si alternative, generatoare sincrone etc.), iar procesele lente sunt cele in care au loc transferuri de masa si caldura, de exempu procesele din cazanele de abur, din instalatiile chimice etc. Ca urmare, in cazul proceselor rapide are loc reglarea automata a unor tensiuni, curenti, turatii etc., in cazul proceselor lente se regleaza temperaturi, presiuni, nivele, debite, compozitii etc.

Deosebirile dintre valorile constantelor de timp si dintre tipul marimilor reglate se reflecta si in constructia regulatoarelor folosite. Datorita acestui fapt, in subcapitolui B apar constructii specifice pentru regulatoarele electronice destinate proceselor rapide si pentru cele destinate proceselor lente.

Regulator centrifug - Comanda turatia unui sistem ethnic, alcatuit dintr-un ax actionat in miscare de rotatie de catre sistem, pe care sunt articulate doua parghii care au cate o greutate la capatul liber. Datorita fortei centrifuge, greutatile se departeaza cu atat mai mult de ax, cu cat viteza de rotatie creata, revenirea in pozitie normal realiziandu-se sub actiunea gravitatiei sau a unor resorturi. Regulatoarele centrifuge comanda, direct sau prin intermediul unui servomotor, dispozitivul de admisie a agentului motor (in cazul motoarelor) sau un dispozitiv de franare (in cazul unor masini sau al unor aparate de transport, de exemplu la funiculare)

Regulator cu plutitor - Regulator pentru mentinerea nivelului unui lichid intr-un revervor, alcatuit dintr-un plutitor care comanda, pe cale mecanica sau electrica, dispozitivul de umplere a rezervorului.

Regulator de avans pentru foraj - Instalatie folosita pentru a regal automat apasarea sapei pe fundul gaurii de sonda. Este alcatuit, in principal, dintr-un motor electric de current continuu, care printr-un reductor si un arbore intermediar, pune in miscare toba de coborat si de ridicat a garniturii de foraj, turatia motorului de avans depinde de incarcarea motorului de foraj, astfel incat, daca acesta are de invins rezistente mari, motorul de avans are o turatie joasa si sapa coboara incet. Cand rezistentele sunt foarte mari, motorul de avans isi schimba sensul de rotatie si sapa este ridicata.

Regulator de inductie - dispozitiv pentru reglarea tensiunii retelelor electrice

Regulator de lampa cu arc - dispozitiv de mentinere a distantei dintre electrozii de carbine ai unei lampi de arc. Regulatorul consta fie dintr-o bobina in serie cu arcul, in interiorul careia se afla o bara de fier moale care sustine unul dintre carbunii arcului, astfel incat, cand distant dintre carbuni creste, curentul din bobina scade si bara este atrasa mai putin in interiorul bobinei, fie dintr-un rheostat in serie cu arcul si dintr-o bobina cu bara de fier moale in derivatie, suportul unuia dintre carbuni fiind comandat de bara de fier care intra mai mult sau mai putin in interiorul bobinei.

Regulator electronic - cuprinde, constructive, elemente electronice.

Capitolul II

Legi de reglare si caracteristici

a)      Legi de reglare tipizate ale regulatoarelor liniare

Schema unei variante simple de sistem de reglare automata (SRA), reprezentata in figura 3.1, include regulatorul automat RA, element de executie EE, instalatia tehnologica IT, traductorul Tr si elementul de comparatie EC (functiunile acestor elemente sunt expuse in manualul "Echipamente electronice pentru automatizari" , clasa a XI-a). Grupand elementele ET, IT si Tr intr-un singur bloc echivalent F - denumit partea fixate a SRA - se obtine aspectul schemei din figura 3.2, cu reactia principal negativa directa (v. manualul citat anterior) ; in acest caz are loc relatia :

a = i - e , (3.1)

unde : e - este marimea reglata, respectiv marimea de iesire a SRA ;

i - marimea de intrare, ale carei valori reprezinta valorile prescrise pentru marimea e ;

a - abaterea .

Blocul F este supus si influentei perturbarii p, care este reprezentata si in figura 3.1, actionand asupra IT.

Din figura 3.2 se constata ca RA primeste la intrare abaterea a si are la iesire marimea de comanda c, in blocul RA avand loc prelucrarea semnalului a dupa o anumita lege (denumita lege de reglare) in scopul obtinerii unei marimi c care sa asigure o functionare cat mai buna a SRA, respectiv cu performante tranzitorii si stationare cat mai ridicate (v. manualul citat mia sus).

La RA liniare se folosesc legi de reglare tipizate, care de peste 50 de ani si-au dovedit eficienta in practica. Principalele legi de reglare tipizate, sunt legile : proportional (P), intergrala (I), proportional-integrala (PI), proportional-derivata (PD) si proportional-intergral-derivata (PID).

In cazul legii, intre marimile c si a - care variaza in timp, deci c c(t) si a  a(t) - se realizeaza o relatie de proportionalitate, de forma :

c = K_Ra, (3.2)

K_R fiind denumit factor de proportionalitate al RA.

Ca urmare, in cazul unei variatii treapta a marimii a, intervenite in momentul t_ , va rezulta pentru marimea c tot o variatie treapta, ca in figura 3.3, in care s-a presupus - pentru ilustrare - valoarea K_R=2.

Astfel, in momentul t_marimea a trece de la valoarea anterioara a₁ la valoarea a₂, ceea ce provoaca trecerea marimii c - practice tot in momentul t_ - de la valoarea anterioara c₁=2a₁ (deci in relatia 3 ^. 2 K_R =2) la valoarea c₂=2a₂.

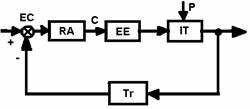
Fig. 3.1. Schema bloc a unui SRA.

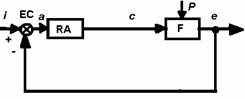
Fig. 3.2. Schema echivalenta a unei bucle de reglare.

Pentru simplificarea reprezentarilor se poate considera :

t (3.3)

si poate face conventia :

a₁ = 0, (3.4)

deci si:

c_r = 2a₁ = 0.

Cu aceste ipoteze si conventia suplimentara de a considera:

a₂ - a₁ = 1,

se obtine (la t > 0) :

c₂ - c₁ = c₂ = c = 2a₂ - 2a₁ = 2a₂ = 2 =K_R, (3.5)

rezultand - in locul reprezentarii din figura 3.3 - reprezentarea din figura 3.4.

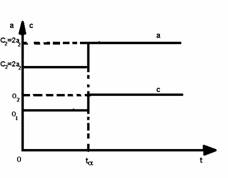
Fig. 3.3. Variatia in timp a marimii de comanda c in cazul variatiei treapta la t= t_a abaterii a.

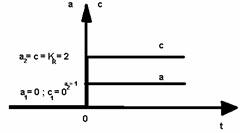
Fig. 3.4. Variatia in timp a marimii de comanda c a unui regulator tip P la o variatie treapta la t < 0 a abaterii a.

Variatia treapta a marimii a din figura 3.4 (cu trecere, la t = 0, de la o valoare anterioara a₁ = 0 la valoarea a₂ = 1) este denumita variatie treapta unitara, avand inaltimea egala cu unitatea.

Din relatia (3.5) si din figura 3.4 se constata ca aplicand la intrarea RA un semnal a treapta unitara se obtine la iesire pentru t > 0 marimea de comanda:

c = K_R. (3.6)

Pe langa variatii treapta, in cadrul SRA se folosesc si variatii liniare cu timpul, denumite variatii rampa, respectiv semnale rampa. Aspectul unei variatii rampa a marimii a este prezentat in figura 3.5 si se constata ca pentru:

t < 0 (3.7)

rezulta :

a = 0 (3.8)

(presupunere analoaga cu cea facuta pentru semnalele treapta din figura 3.4), iar pentru:

t > 0 (3.9)

se obtine :

a = kt (3.10)

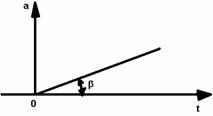
Fig. 3.5. Variatia rampa a abaterii a.

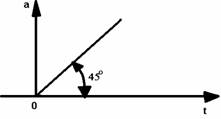
Fig. 3.6. Variatia rampa unitara a abaterii a.

unde :   

k = tg  (3.11)

(v. fig. 3.5) este coefficient unghiular.

In cazul in care:

 = 45^o (3.12)

se obtine semnalul denumit rampa unitara (fig. 3.6), definit de relatia :

a = t (3.14)

pentru t > 0.

Daca unui regulator proportional, care realizeaza legea de reglare (3.2), I se aplica la intrarea semnalul rampa unitara (3.14) atunci se obtine la iesirea RA marimea de comanda :

c = K_Rt (3.15)

-pentru t > 0 - conform cu relatiile (3.2) si (3.14).

Presupunand, ca si mai inainte, K_R = 2, in figura 3.7 sunt reprezentate marimile a = t si c = 2t de la intrarea si iesirea RA. La fiecare moment, comanda c are valoarea :

c = 2a. (3.16)

intrucat :

a = t.

si :

c = 2t = 2a ,

la t = t_ rezulta :_

a = t_

si :

c = 2 t_.

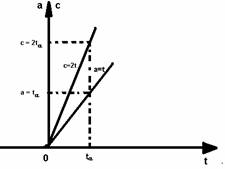
Fig. 3.7. Variatia in timp a marimii de comanda c a unui regulator tip P la o variatie rampa unitara a abaterii a pentru K_R = 2.

In cazul legii I, intre marimile c si a se realizeaza relatia :

c = 1/T _S a dt , (3.15)

unde T, este constanta de timp a componentei integrale.

Din relatia (3.17) se constata ca marimea de comanda c are valori proportionale cu integrala (in raport cu timpul) abaterii a .

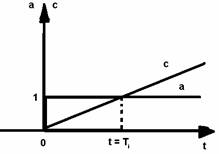
Fig. 3.8. Variatia in timp a marimii de comanda c a unui regulator de tip I la o variatie treapta unitara a abaterii a .

Presupunand ca abaterea este un semnal treapta unitara, cu a = 1 = const pentru t > 0, rezulta :

c = 1/T_{i S} a dt = 1/T_{i S} a dt = 1/T_i ^. t (3.18)

(pentru t > 0), deci se obtine la iesirea RA un semnal rampa, cu coeficientul unghiular 1/T_i. Reprezentand figura 3.8 semnalele respective a si c, se constata ca la momentul :

t = T_i

se obtine :

c = 1/T_i ^. T_i = 1 = a , (3.19)

marimea de comanda c atingand valoarea abaterii a = I.

In cazul legii PI marimea de comanda c rezulta prin insumarea a doua component, una proportional c_p si una integral c_I , avand expresia :

c = c_p + c_I = K_R(a + 1/T_{i S} a dt) = K_Ra + K_R/T_{i S} a dt ;    (3.20)

din relatia (3.20) se obtine :

c_p = K_Ra (3.21)

si    c_I = K_R/T_{i S} a dt. (3.22)

In ipoteza ca abaterea a este un semnal treapta unitara, din (3.21) si (3.22) rezulta pentru t > 0 (cand a = 1 = const) :

C_p = K_R, (3.23)

c_I = K_R/T_{i S} dt = K_R/T_i ^. t (3.24)

si :

c = c_p + c_I = K_R/T_i ^.t = K_R(1 + 1/T_i ^. t). (3.25)

In figura 3.9 sunt reprezentate marimile a,c_p , c_I si c corespunzatoare acestor relatii. Din expresia (3.25) se constata ca pentru t = T_i se obtine :

c = K_R (1 + 1/T_i ^. T_i) = 2K_R (3.26)

relatie confirmata si in figura 3.9 datorita valorii c = 2K_R , constanta de timp T, este denumita si "timp de dublare" a valorii marimii c ca urmare a prezentei componentei integrale c_I.

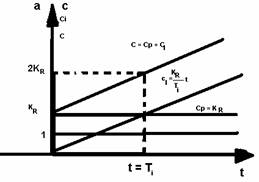
Fig. 3.9. Variatia in tmp a marimii de comanda c = c_p + c_I a unui regulator tip PI la o variatie treapta unitara a abaterii a.

In cazul legii PD marimea de comanda c are o component proportional cu c_p - cu expresia (3.21)

si o coponenta derivative c_p , proportional cu derivata abaterii si definita de relatia :

c_D = K_RT_d da/dt , (3.27)

unde T_d este constanta de timp a componentei derivative.

Insumand cele doua component - din expresiile (3.21) si (3.27) - se obtine marimea de comanda:

c = c_p + c_D = K_Ra + K_RT_d da/dt =K_R(a + T_a da/dt). (3.28)

Presupunand ca la intrarea RA se aplica un semnal a treapta unitara, cu a = 1 = const la t > 0 , din relatiile (3.21) si (3.27) se obtine (pentru t > 0 ) :

c_p = K_Ra =K_R . (3.29)

c_D = K_RT_d da/dt = 0 (3.30)

Inlocuind expresiile (3.29) si (3.30) in relatia (3.28) se obtine (pentru t > 0) :

c = K_{R .} (3.31)

deci aceeasi valoare ca in expresiile (3.6) si (3.23), corespunzatoare regulatorului proportional si componentei proportionale a regulatorului PI ; rezulta astfel ca pentru t > 0 componenta derivative c_D nu intervine.

Aceasta component intervine chiar in momentul t = 0, cand semnalul a trece brusc de la valoarea zero la valoarea 1, variatie specifica treptei unitare. Datorita formei de variatie in timp a treptei,acest semnal nu este derivabil la t = 0, dar constatand ca in momentul t = 0 viteza de variatie a marimii a tinde catre infinit (intrucat la t = 0 valoarea a trece brusc de la valoarea zero la valoarea 1) se desprinde concluzia ca derivate da/dt - care caracterizeaza viteza de variatie - tinde catre infinit la t= 0 si revine intr-un timp infinit mic (considerat tot la t = 0) la valoarea nula.

Avand in vedere considerentele facute, rezulta ca variatia in timp a componentei c_D - din relatia (3.30) - are aspectul din figura 3.10. Ca urmare, efectuand suma din expresia (3.28) si tinand seama de relatia (3.29), se obtine pentru marimea c variatia din figura 3.11.

Semnalul din figura 3.10 este numit impuls de tip Dirac si se constata ca variatia in timp a marimii c din figura 3.11 se obtine prin insumarea unui asemenea impuls cu un semnal treapta.

Fig. 3.10. Reprezentarea unui semnal impuls Dirac (variatia in timp a componentei derivative c_D).

Observatie. Reprezentarile din figurile 3.3 . 3.11 corespund unor considerente teoretice, dar ele ilustreaza numai aproximativ variatiile marimilor care au loc in practica, intrucat valorile acestor marimi sunt totdeauna finite,datorita limitarii energiilor disponibile si fenomenelor de saturatie. Variatiile reale ale marimilor de comanda c sunt reprezentate in figurile 3.13 . 3.17.

In cazult legii PID marimea de comanda c are trei componente (proportionala c_p, intergrala c_I si derivativa c_D ), definite de expresiile anterioare :

C_p = K_Ra ;

c_I = K_R/T_{i S} adt,

c_D = K_RT_i da/dt

si rezultand:

c = c_p + c_I + c_p = K_R(a + 1/T_{I S} adt ) + T_d da/dt .    (3.32)

Presupunand ca abaterea a este un semnal treapta unitara, variatia in timp a marimii c -reprezentata in figura 3.12 - rezulta prin insumarea marimilor c_p + c_I din figura 3.9 cu marimea c_p din figura 3.10.

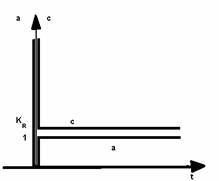
Fig. 3.11. Variatia in timp a marimii de comanda c a unui regulator tip PD la o variatie treapta unitara a abaterii a.

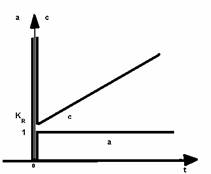
Fig. 3.12. Variatia in timp a marimii de comanda c a unui regulator tip PID la o variatie treapta unitara a abaterii a.

In figurile 3.13, 3.14, 3.15, 3.16 si 3.17 sunt reprezentate aspectele variatiilor reale ale marimilor de comanda pentru regulatoarele P, I , PI , PD si PID, tinand seama de faptul ca aceste marimi nu pot avea variatii de tip treapta (datorita unor mici intarzieri evitabile in transmiterea semnalelor chiar in interiorul RA, la o abatere a de tip treapta marimea c nu poate avea tot o variatie treapta, intrucat ar rezulta o transmitere instantanee a semnalului de la intrarea la iesirea RA), precum si de limitarea semnalelor, mentionate anterior.

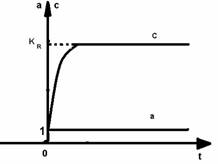
Fig. 3.13. Variatia reala a marimii de comanda c a unui regulator tip P la o variatie treapta unitara a abaterii a.

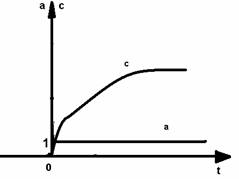
Fig. 3.14. Variatia reala a marimii de comanda c a unui regulator tip I la o variatie treapta unitara a abaterii a.

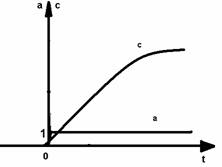
Fig. 3.15. Variatia reala a marimii de comanda c a unui regulator tip PI la o variatie treapta unitara a abaterii a.

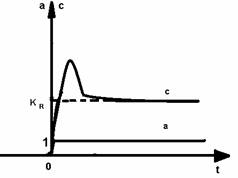
Fig. 3.16. Variatia reala a marimii de comanda c a unui regulator tip PD la o variatie treapta unitara a abaterii a.

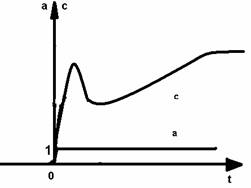
Fig. 3.17. Variatia reala a marimii de comanda c a unui regulator tip PID la o variatie treapta unitara a abaterii a.

b)     Caracteristici tipizate ale regulatoarelor neliniare

Cele mai utilizate regulatoare neliniare sunt regulatoarele bipozitionale (RBP) si regulatoarele tripozitionale (RTP). Dupa cum s-a mentionat in subcapitolul A, paragraful 1, punctual c, functionarea regulatoarelor neliniare este caracterizata - in regim stationar - de o dependenta neliniara intre marimea de comanda c si abaterea a ; aceasta dependent este denumita si caracteristica static, pentru a se sublinia ca este valabila numai in regimul stationar.

In cazul regulatoarelor bipozitionale caracteristica static ideala (care nu se realizeaza exact in practica) are aspectul din figura 3.18 si este denumita si caracteristica ideala de releu, intrucat functionarea RBP este similara cu a releelor, de multe ori constructia RBP incluzand un releu.

Din aspectul caracteristicii se constata ca daca valorile abaterii a satisfac conditia :

a > 0,

la iesirea RBP se obtine marimea de comanda :

c = c_max = const > 0, (3.33)

iar pentru :

a > 0,

rezulta :

c = 0. (3.34)

Denumirea de regulator bipozitional se datoreaza faptului ca marimea de comanda poate avea - in regim stationar - numai cele doua valori din expresiile (3.33) (desi aspectul graphic al caracteristicii din figura 3.18 este analog cu cel al semnalelor treapta din figura 3.4, deosebirea esentiala consta in faptul ca figura 3.4 are timpul t in axa absciselor - deci reprezinta o evolutie dinamica, in timp - iar figura 3.18 are abaterea a in axa absciselor, reprezentand o dependent de regim stationar, deci static).

In realitate, regulatoarele bipozitionale - ca si releele - nu au o caracteristica ideala, ci o caracteristica cu histerezis (fig. 3.19), valorile marimii de comanda c depinzand si de sensul de variatie - crestere sau descreste - a abeterii a . Astfel, cand abaterea a creste, trecerea la valoarea c = 0

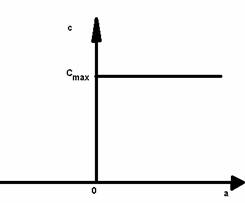
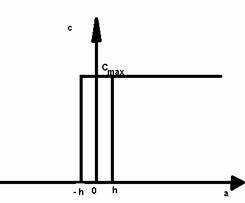
Fig. 3.18. Caracteristica ideala de releu a    Fig. 3.19. Caracteristica reala de releu cu regulatorului bipozitional histerezis a regulatorului bipozitional

la valoarea c= c_max nu are loc pentru conditia anterioara a > 0, ci pentru conditia :

a > h,

unde h este jumatatea latimii ciclului de histeris.

De asemenea, daca c = c_max si marimea a scade, trecerea la valoarea c = 0 nu are loc pentru conditia anterioara a < 0, ci pentru conditia :

a < - h.

In cazul regulatoarelor tripozitionale caracteristica static are aspectul din figura 3.20 (neglija nd prezenta unor cicluri de histerezis, existente la trecerile de la valorile c = - C_max la c = 0 - si invers - si de la valroile c = 0 la c = C_max si invers)

Se constata ca daca are loc conditia : -z_i < a < z_i , (3.35)

atunci se obtine : c = 0 , (3.36)

deci marimea de comanda este nula.

Pentru:    a > z_i , (3.37)

rezulta:    c = c_max , (3.38)

iar pentru :    a < - z_i , (3.39)

se obtine:    c = -c_max , (3.39')

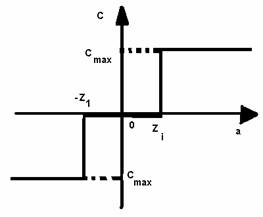
Fig. 3.20. Caracteristica ideala a regulatorului tripozitional

Marimea de comanda c poate avea trei valori ( -c_max , 0 , C_max ), cea ce a determinat denumirea de regulator tripozitional (RTP).

Zona valorilor abaterii a definite de relatia (3.35) este denumita zona de insensibilitate , deoarece pentru valori ale abaterii in interiorul zonei se obtine o marime de comanda e nula la iesirea RTP, conform relatiei (3.36).

Capitolul III

Solutii constructive de implementare a legilor de reglare

Obtinerea legii P.

Legea de reglare de tip P se obtine, in prima ipoteza, prin schema din figura 3.23, care contine rezistenta R₁ in circuitul de intrare si rezistenta R₂ in circuitul de reactive negative locala. Tensiunea de intrare a regulatorului P este notate cu u_1, cea de iesire cu u₂, iar tensiunile bornelor inversoare si neinversoare sunt notate cu u_i si u_n ; intrucat borna neinversoare este legata direct la masa, rezulta

u_n (3.40)

Considerand ca tensiunea de intrare are polaritatea :

u_i = 0 , (3.41)

rezulta de asemenea :

u_i (3.42)

iar tensiunea de iesire va avea polaritatea:

u (3.43)

tensiunea de iesire fiind de polaritate opusa polaritatii tensiunii bornei inversoare.

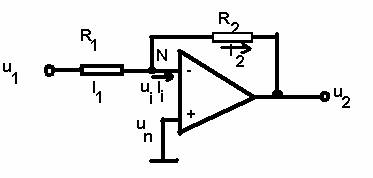
Fig 3.23. Schema unui bloc de reglare tip P cu semnalul de intrare aplicat la borna inversoare.

Polaritatile considerate determina circulatia curentilor I₁, I₂ si I_i in sensurile reprezentate in figura 2.23, curentul I, circuland prin rezistenta de intrare a AOCI.

Obtinerea legii I .

Pentru obtinerea unei legi de reglare de tip integral ( I ) se foloseste schema din figura 3.25, cu aplicarea semnalului de intrare la borna inversoare, cu o rezistenta R₁ in circuitul de intrare si o capacitate C₂ in circuitul de reactive.

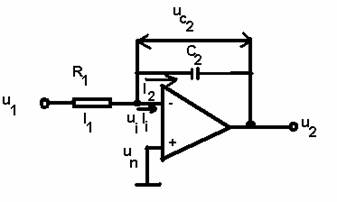
Fig 3.25. Schema unui bloc de regalre tip I.

Obtinerea legii D.

Legea de tip derivative (D) nu se foloseste separat, dar component derivative intervine in PD si PID. Pentru obtinerea unei legi D se foloseste schema din figura 3.26, cu folosirea bornei de intrare inversoare, cu capacitatea C₁ in circuitul de intrare si cu rezistenta R₂ in circuitul de reactive ; datorita schimbarii pozitiilor rezistentei si capacitatii ( in raport cu schema din figura 3.25 ), in care locul unui efect de integrare se obtine un efect de derivare.

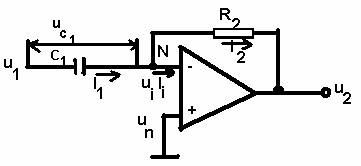
Fig 3.26. Schema unui bloc de reglare tip D.

Obtinerea legii PI

In cazul aplicarii semnalului de intrare la borna inversoare, legea PI poate fi obtinuta combinarea schemelor din figurile ( care asigura separate componentele P si I ), rezultand schema din figura 3.27.

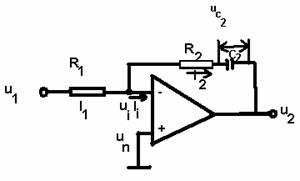
Fig 3.27. Schema unui bloc de reglare tip PI.

Obtinerea legii PD.

Aplicand semnalul de intrare la borna inversoare, legea PD se obtine prin combinarea schemelor din figurile 3.23 si 3.26 ( care asigura separate componentele P si D ), rezultand schema din figura 3.30.

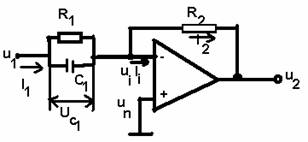
Fig. 3.30. Schema unui bloc de reglare tip PD cu semnalul de intrare aplicat la borna inversoare.

Obtinerea legii PID.

Folosind borna inversoare pentru aplicarea semnalului de intrare, legea PID se obtine prin combinarea schemelor din figurile 3.27 si 3.30 ( care asigura sparat legi PI si PD ), rezultand schema din figura 3.32.

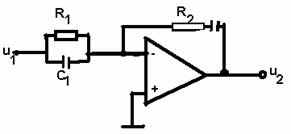
Fig. 3.32. Schema unui bloc de reglare tip PID cu semnal de intrare aplicat la borna inversoare.

Bibliografie

1. Sergiu Calin, Aurel Pascu, Stelian Popesc - Echipamente Electronice Pentru Automatizari ( Editura Didactica si Pedagogica), Bucuresti 1985

2. https://www.regielive.ro