Structura mecanismelor

STRUCTURA MECANISMELOR

OBIECTIVE

a)      Explicitarea algoritmilor de modelare structurala a mecanismelor, pe baza unor exemple intuitive, in abordare simultana cu celelalte obiectivele operationale si anume:

b)      Definirea si interpretarea corecta a notiunilor de baza, in contextul corelatiilor specifice dintre acestea;

c)      Decelarea marimilor intrinseci care descriu starea structurala a unui mecanism;

d)     Generarea modulara de mecanisme complexe prin agregarea de mecanisme simple.

O masina contine: un efector, un motor electric, un mecanism.

	mecanism

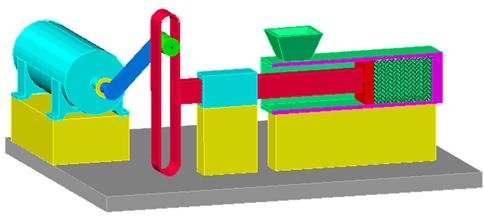
a

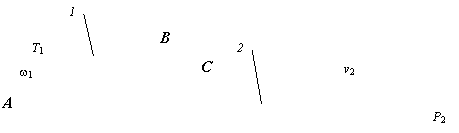
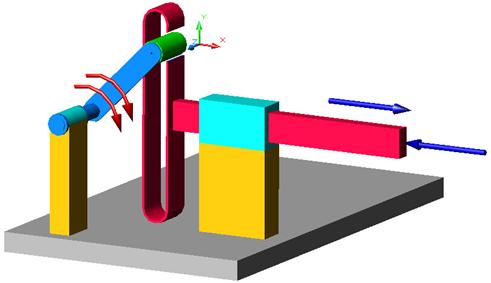
b

Fig.  a - exemplu de masina: motor - mecanism sinus - efector b - mecanismul sinus si legaturile exterioare ale acestuia, in urma izolarii din masina.

1. Schema structurala a unui mecanism (fig. 1.2,b₁ si c₁): reprezentare simplificata, realizata fara masuratori, prin care sunt puse in evidenta:

a)        elementul de referinta (baza) si elementele cinematice (mobile) ale mecanismului;

b)       cuplele cinematice dintre elemente, in conformitate cu ordinea si pozitia relativa reala;

c)        intrarile si iesirile mecanismului, cu parametrii exteriori corespunzatori;

d)       triedrul de referinta atasat mecanismului.

Precizari 1) Daca schema structurala tine seama si de dimensiunile elementelor (este reprezentata la scara), aceasta devine schema cinematica. 2) Daca, in plus, sunt incluse si informatiile care descriu distributia maselor, coeficientii de elasticitate, coeficientii de amortizare si coeficientii de frecare, schema cinematica devine schema dinamica.

C

B

A

P

a

T

v

w

C

B

A

v

P

b

T

w

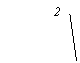
A

B

C

v

w

P

T

c

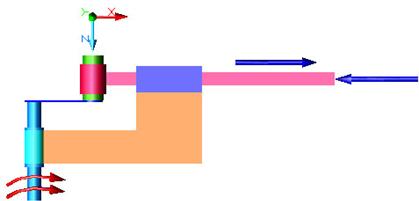
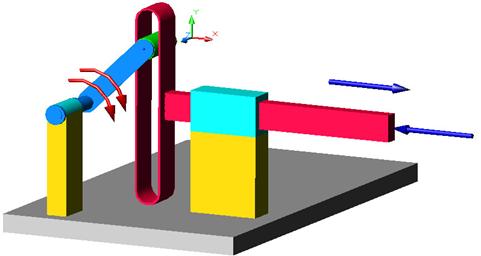
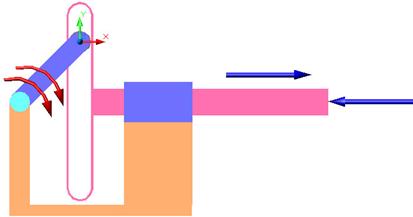
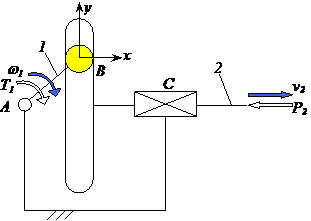
Fig.  a b c Mecanismul sinus: a - reprezentare axonometrica;
b - vedere frontala; c - vedere de sus.

b1

c1

d

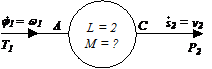
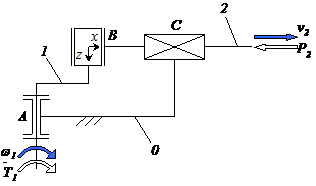
Fig.  b c d Mecanismul sinus: b₁ - schema structurala in vedere frontala; c₁ - schema structurala in vedere de sus; d) schema bloc.

B

A

C

a

P

T

v

w

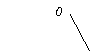
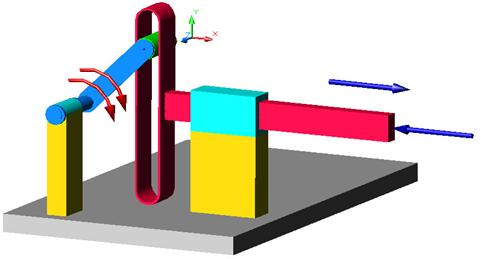
B

C

A

b1

b3

b2

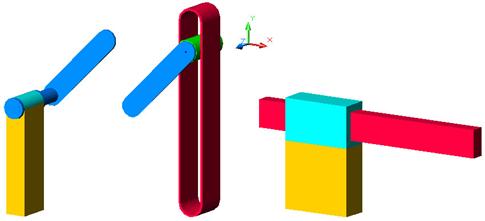
Fig.  Cuplele mecanismului sinus: a - mecanismul sinus; b₁ - cupla de rotatie A≡ (0,1); b₂ - cupla cilindru pe plan A≡ (1,2); b₃ - cupla de translatie C≡ (2,0).

1. Cupla cinematica (fig. 1.3,b₁, b₂ si b₃): monocontact direct si mobil dintre doua elemente. Conform definitiei, doua elemente libere si, de asemenea, doua elemente solidarizate nu sunt cuple cinematice! Modelarea structurala a unui cuple, dintr‑un mecanism, presupune, mai intai, izolarea acesteia din mecanism (v. tab.1.1).

2. Mobilitati (libertati) si legaturi (contrangeri): Considerand, mai intai, un sistem de doua elemente libere si un triedru de referinta, un element al sistemului:

poate efectua, fata de celalalt, f = 6 miscari independente: trei miscari de translatie (v_x, v_y, v_z) si trei de rotatie (w_x w_y w_z) si, evident,

nu poate transmite, celuilalt element, forte (si momente): P_x = P_y = P_z = M_x = M_y = M_z = 0.

Acest sistem are f = 6 grade de mobilitate (sau de libertate) si implicit c = 0 grade de legatura (sau de constrangere).

Considerand acum un sistem de doua elemente solidarizate si un triedru de referinta, un element al acestui sistem:

poate transmite, celuilalt, c = 6 forte si momente independente (P_x, P_y, P_z, M_x, M_y, M_z ) si, evident,

nu se poate misca, fata de celalalt: v_x = v_y = v_z = w_x w_y w_z

In acest caz, sistemul are c = 6 grade de legatura (sau de constrangere) si implicit f = 0 grade de mobilitate (sau de libertate).

Concluzii:

a)       intr‑o cupla cinematica, ca si in sistemele precedente, f + c = 6, dar, spre deosebire de acestea, 1 f 5 si reciproc 5 c

b)       fiecare grad de mobilitate este caracterizat printr‑o miscare relativa independenta si, implicit, printr‑o forta de legatura dependenta (in particular, nula);

c)        fiecare grad de legatura este caracterizat printr‑o forta de legatura independenta si, implicit, printr‑o miscare relativa dependenta (in particular, nula);

d)       legaturile mobile dintre elemente sunt caracterizate prin miscari si forte reciproce, adica: unei miscari independente ii corespunde o forta de legatura dependenta si reciproc, unei forte independente ii corespunde o miscare relativa dependenta;

e)        notiunea de grad de libertate este o notiune generala, valabila pentru sisteme de orice natura; pentru sistemele stereomecanice, libertate inseamna de fapt mobilitate (adica, posibilitate de miscare relativa independenta) si ca urmare, notiunea de grad de mobilitate constituie o "traducere directa" a notiunii generale, aplicabila numai in cazul sistemelor stereomecanice.

3. Starea structurala a unei cuple X, izolata din mecanism (tab.1.1), poate fi modelata prin:

3a₁ Gradul de mobilitate f_X, prin care se arata cate dintre cele sase miscari initial independente (cand un element era liber fata de celalalt) mai raman independente prin punerea celor doua elemente in contact;

3a₂ Baza miscarilor independente (f_X), prin care sunt nominalizate cele f_X miscari independente, intr‑un anumit triedru de referinta.

3b₁ Gradul de legatura sau de constrangere c_X, care indica cate dintre cele sase miscari initial independente (cand un element era liber fata de celalalt), devin dependente prin punerea celor doua elemente in contact; fiecare dependenta este exprimata uzual printr‑o ecuatie si modeleaza o constrangere sau o legatura^*); d.p.d.v. static, c_X desemneaza numarul fortelor (si momentelor) independente care pot fi transmise, prin contact, de la un element la celalalt;

3b₂) Baza fortelor independente (c_X), care nominalizeaza cele c_X forte (si momente) independente, intr‑un anumit triedru de referinta.

3c) Tipul contactului dintre elementele cuplei. Se deosebesc doua situatii distincte:

a)        suprafetele conjugate, prelucrate in cele doua elemente ale cuplei, sunt congruente (se pot suprapune perfect una peste cealalta) si

b)       suprafetele conjugate sunt incongruente.

In cazul a) se obtine un contact de tip suprafata, denumit contact congruent (sau inferior , iar in cazul b) rezulta un contact de tip liniar sau punctiform, denumit contact incongruent (sau superior .

3d) Tipul inchiderii cuplei. Inchiderea cuplei se refera la mentinerea contactului permanent dintre elemente; aceasta mentinere poate fi realizata in doua moduri: a) prin forma elementelor si b) prin intermediul unei forte de inchidere (greutatea unui element, forta unui arc etc.). Ca urmare, se deosebesc: a) inchiderea cuplei prin forma (v. tab. 1.1,a.e) si b) inchiderea cuplei prin forta (v. tab. 1.1,f si g).

1. Legatura redundanta (cinematic): legatura care nu influenteaza starea de miscare a unui sistem; o legatura redundanta este nedeterminata static, deoarece introduce o forta care, in premisa elementelor rigide, nu poate fi calculata. Astfel de legaturi pot sa apara numai in lanturile cinematice inchise.

C

a

B

A

= = = = = 0

B

b

A

C

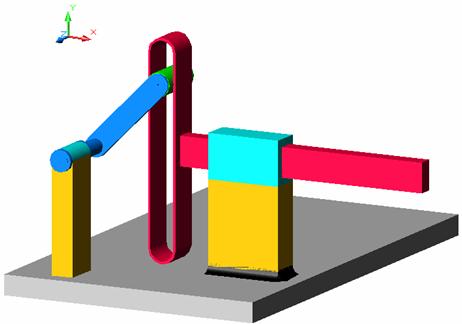
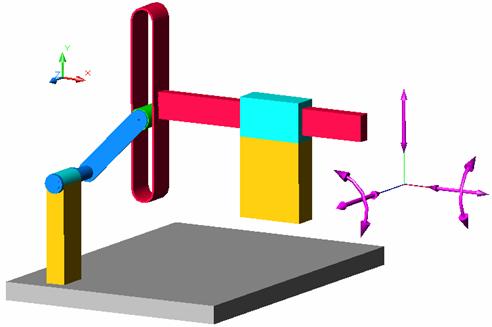
Fig.  a - lantul simplu deschis generat prin ruperea bazei mecanismului sinus; b - lantul inchis obtinut prin sudarea elementelor extremale.

vx

wz

vy

wy

vx

b

a

vy

wz

wx

wz

vy

wz

d

c

Fig.  Miscarile independente dintre elementele extremale ale unui lant simplu deschis: a - lant cu cel putin 3 rotatii paralele; b - lant cel putin 3 rotatii paralele si translatii perpendiculare pe rotatii; c - lant cu doua rotatii paralele; d - lant cel putin 3 rotatii concurente intr‑un punct fix.

2. Miscarile independente dintre elementele extremale pot fi determinate intuitiv pe baza urmatoarelor precizari (v. fig. 1.5):

2a) Daca cuplele lantului simplu deschis materializeaza cel putin 3 rotatii paralele, cu o axa z (fig. 1.5,a), sau cel putin 3 rotatii si translatii (fig. 1.5,b), in care rotatiile sunt paralele cu z si translatiile sunt perpendiculare pe z, atunci elementul final efectueaza, fata de elementul initial, o miscare plan paralela caracterizata prin 3 miscari independente: v_x, v_y, w_z

2b) Daca cuplele lantului simplu deschis materializeaza 2 rotatii paralele (fig. 1.5,c), atunci elementul final efectueaza, fata de elementul initial, 2 miscari independente instantanee: o rotatie si o translatie perpendiculara pe planul format de axele celor 2 rotatii;

2c) Daca cuplele lantului simplu deschis materializeaza cel putin 3 rotatii concurente intr‑un punct fix O (fig. 1.5,d), atunci elementul final efectueaza, fata de elementul initial, o miscare sferica caracterizata prin 3 miscari independente: w_x w_y w_z.Cu ajutorul precizarii 2a), baza miscarilor independente (f_3,0), dintre elementele extremale 3 si 0 (fig. 1.4,a), poate fi determinata intuitiv astfel:

Considerand ca in cuplele lantului deschis ar exista numai mobilitatile (w_z)_A, (w_z)_B, (v_y)_B si (v_x)_C, atunci elementul final ar efectua, fata de elementul initial, o miscare plan paralela, caracterizata prin 3 miscari independente: v_x, v_y, w_z

In lantul deschis real (fig. 1.4,a), elementul final efectueaza, fata de cel initial, inca 2 miscari independente: o translatie v_z , permisa de cupla B, si o rotatie w_x, permisa, de asemenea, de cupla B.

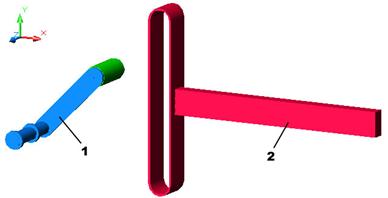
a

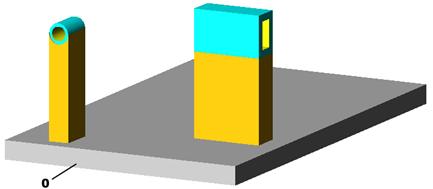
b

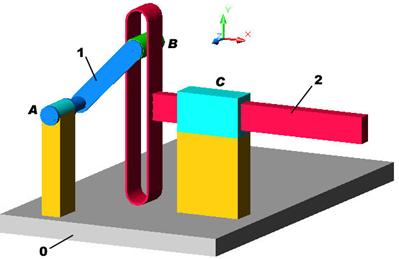
Fig.  a,b Identificarea intuitiva a gradului de mobilitate M al unui mecanism: a - eliberarea elementelor cinematice de legaturi;
b - reconsiderarea legaturilor din mecanism.

c

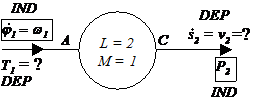
Fig.  c - schema bloc a mecanismului cu parametrii exteriori independenti si dependenti

Gradul de mobilitate M al unui mecanism are urmatoarele semnificatii:

a)        D.p.d.v. geometric, M reprezinta numarul coordonatelor (unghiulare si/sau liniare) care determina complet pozitiile tuturor elementelor cinematice fata de baza; cu alte cuvinte, d.p.d.v. geometric, M reprezinta numarul coordonatelor independente ale mecanismului.

b)       D.p.d.v. cinematic, M reprezinta numarul miscarilor independente ale elementelor cinematice fata de baza (celelalte miscari, fiind dependente, pot fi determinate in functie de primele). Tinand seama ca miscarile independente sunt controlate din exteriorul mecanismului, rezulta ca M arata cate dintre miscarile exterioare ale mecanismului sunt independente.

Tabelul 1.2. Modelarea structurala, pe etape, a mecanismului sinus (prezentarea sintetica)

A

B(cilindru pe plan)

C

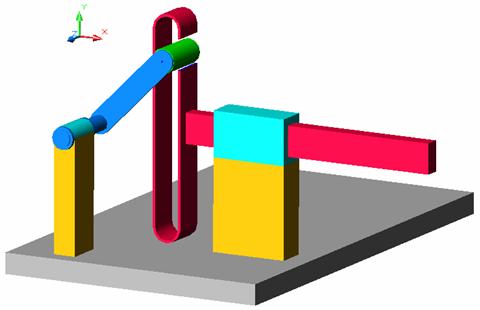
a

C

B(sfera pe plan)

A

b

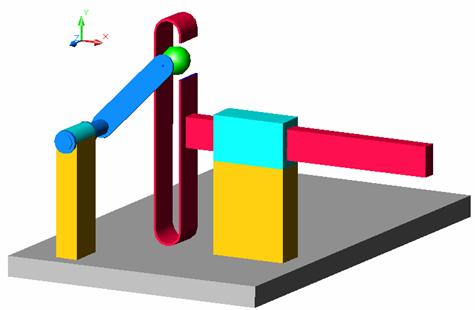
Fig.  a b Mecanismul sinus: a - mecanism hiperstatic (S = 1);
b - varianta izostatica.

C

B(sfera pe plan)

A

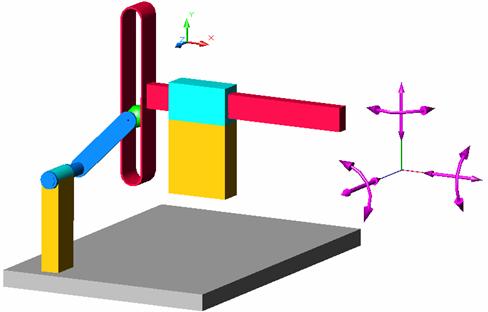
c

Fig.  c Mecanismul sinus: c - lantul cinematic deschis asociat mecanismului izostatic.

PARTICULARITATILE MODELARII STRUCTURALE A MECANISMELOR COMPLEXE DE TIP POLICONTUR

a

b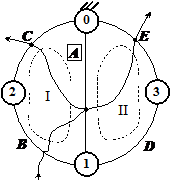

c

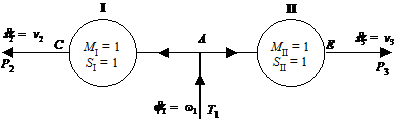
d

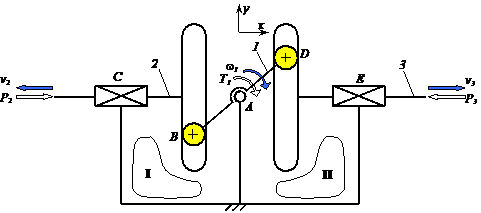
Fig.  Mecanism bicontur format prin legarea in paralel a doua mecanisme sinus: a - schema structurala; b - graful structural;
c - schema bloc; d - izolarea mecanismelor componente.

1. Graf structural: reprezentare simplificata a unui mecanism, in care elementele sunt reprezentate prin cerculete (care formeaza varfurile sau nodurile grafului), iar cuplele sunt reprezentate prin arce de legatura (v. fig. 1.9,b); evident un mecanism cu n elemente cinematice (mobile) are  = n + 1 varfuri si a arce de legatura.

Numarul ciclomatic al grafului, q = a -  +1, desemneaza numarul de contururi independente continute in graf; pentru simplitate, in alegerea acestor contururi sunt preferate cele cu numar minim de laturi (arce). Contururile independente din graf permit identificarea directa a mecanismelor monocontur din componenta mecanismului complex.

Arcele comune, ale contururilor independente stabilite, desemneaza cuplele comune dintre mecanismele componente si gradul de multiplicitate al acestora: o cupla comuna pentru m_k contururi are gradul de multiplicitate m_k - 1 (este comuna de m_k - 1 ori).

La randul lor, cuplele comune (prin gradul de mobilitate f_k,com si prin gradul de multiplicitate m_k - 1) desemneaza numarul L_c al legaturilor exterioare comune dintre mecanismele componente, denumit prescurtat numar de cuplari:

L_c S( m_k - 1)  f_k,com cuplari.

Printr‑o cuplare (sau legatura exterioara comuna), a doua mecanisme componente, devin egale doua miscari exterioare: o miscare dintr‑un mecanism component cu o miscare din celalalt mecanism component; in cazul general, printr‑o astfel de cuplare dispare o miscare independenta (devine dependenta).

In cazul exemplului analizat (fig. 1.9,c si d), prin cuplarea, materializata de cupla comuna A, devin egale 2 miscari independente: w ^I w ^II; ca urmare, din cele 2 miscari initial independente (fig. 1.9,d), dupa cuplare ramane numai una (fig. 1.9,b): w

Modelarea structurala a mecanismelor componente
(etapa a II‑a)

Conform schemei structurale din fig. 1.9,a, cele doua mecanisme componente (I si II) sunt mecanisme de tip sinus, cu o cupla incongruenta, care d.p.d.v. structural sunt identice. Modelarea structurala a acestui tip de mecanism a fost explicitata in subcap. 1.3.

Gradul de mobilitate M al mecanismului complex
(etapa a III‑a)

In varianta cea mai simpla, gradul de mobilitate al mecanismului complex se obtine extinzand relatia mecanismului monocontur, prin trecerea de la un contur la mai multe contururi :

M = 6n - (Sc - c*) => M = 6n - (Sc Sc (1.2)

In cazul exemplului analizat rezulta:

M = 6n - (Sc Sc*) = 6n - [(c_A + c_B + c_C + c_D + c_E) - (c*_I + c*_II)] = 63 - [(5 + 2 + 5 + 2 + 5) - (1 + 1)] = 1 => o miscare exterioara independenta (j w e ) si, implicit, un moment exterior dependent: T₁ = T₁( ).

O alta modalitate de calcul a gradului de mobilitate M rezulta din analiza schemei bloc a mecanismului complex (fig. 1.9,c si d):

• mecanismele componente, considerate izolate (fig. 1.9,d), formeaza un sistem mecanic cu gradul de mobilitate:
  SM_k = M_I + M_II = 1 + 1 = 2;
• prin introducerea cuplarilor intre mecanismele componente (fig. 1.9,c), in cazul general, sunt eliminate L_c miscari independente; ca urmare, mecanismului complex ii ramane gradul de mobilitate (fig. 1.9,c):

M SM_k - L_c= M_I + M_II - L_c = (1 + 1) - 1 = 1 => o miscare exterioara independenta (j w e ) si, implicit, un moment exterior dependent: T₁ = T₁( ).

Analiza parametrilor exteriori si stabilirea calitativa a functiilor de transmitere (etapa a IV‑a)

Conform fig. 1.10,a si b, mecanismul complex analizat are L = 3 legaturi exterioare, adica are L = 3 miscari exterioare si L = 3 forte si momente exterioare; analiza acestor parametri exteriori se bazeaza pe interpretarea cinematica si statica a gradului de mobilitate M:

a) Dintre cele L = 3 miscari exterioare, M = 1 este independenta: de exemplu, miscarea de intrare: (j w = dj /dt, e = dw /dt ); pentru a fi recunoscuta usor, miscarea independenta a fost incadrata (fig. 1.10,b).

Miscarile exterioare ramase, L - M = 3 - 1 = 2 (s₂ si s₃), sunt dependente si descriu calitativ 2 functii de transmitere a miscarilor; fiecare dintre acestea poate fi exprimata in cele trei moduri reductibile intre ele:

s = s₂(j ) => v₂ = ds₂/dt = v₂(j w ) => a₂ = dv₂/dt = a₂(j w e

s = s₃(j ) => v₃ = ds₃/dt = v₃(j w ) => a₃ = dv₃/dt = a₃(j w e

b) Dintre cele L = 3 forte (si momente) exterioare, M = 1 este dependenta: de exemplu, momentul de intrare: T₁.

a

b

c

d

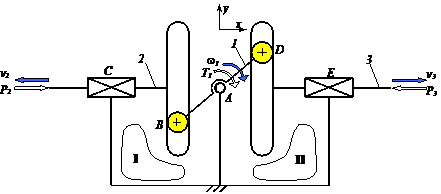
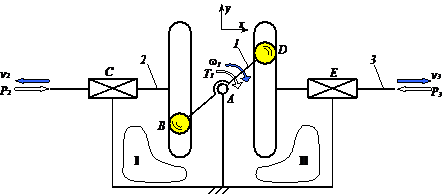
Fig.  Mecanisme bicontur: a - schema structurala a mecanismului complex hiperstatic; b - schema bloc, cu precizarea calitativa a functiilor de transmitere; c - schema structurala a unei variante izostatice;
d - schema bloc asociata variantei izostatice.

Ca urmare, fortele exterioare ramase, L - M = 3 - 1 = 2 (P₂, P₃), sunt independente si pentru a fi recunoscute usor, au fost incadrate (fig. 1.10,b); dependenta T₁ = T₁(j , P₂, P₃) desemneaza calitativ functia de transmitere a fortelor.

Stabilirea cantitativa a functiilor realizate de mecanism, pentru transmiterea miscarilor si a fortelor, reprezinta obiective principale pentru modelarea cinematica si, respectiv, dinamica a mecanismului.

Gradul de nedeterminare statica a mecanismului complex si propuneri de solutii determinate static
(etapa a V‑a)

In cazul general, gradul de nedeterminare statica S al mecanismului complex se obtine prin insumarea legaturilor redundante (nedeterminate static) din mecanismele componente.

Tinand seama de rezultatele obtinute in subcapitolul 1.3, in cazul exemplului din fig. 1.10 se obtine gradul de hiperstaticitate:

S = S_I + S_II = 1 + 1 = 2 legaturi static nedeterminate,

de ecuatii: w_yI = 0 si w_yII

Eliminarea acestor legaturi, atunci cand devin defecte structurale, se realizeaza introducand in mecanismele monocontur I si II cate o mobilitate w_y. Folosind solutia de eliminare descrisa in subcapitolul 1.3, se obtine mecanismul complex izostatic reprezentat in fig. 1.10,c si d.

Sa se efectueze analiza structurala pe etape a mecanismelor monocontur din fig. 1.11, conform modelului expus in subcap. 1.3 si prezentat succint in tab. 1.2.

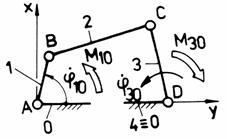
a a₁

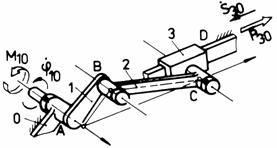
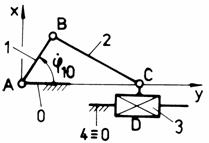
b b₁

   

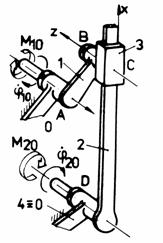
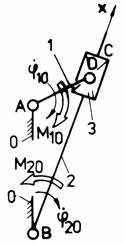
c c₁

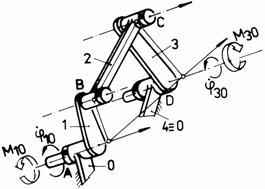
Fig.  Tema de casa: a,a₁ - mecanismul patrulater plan manivela-balansier; b,b₁ - mecanism plan manivela-culisor cu biela; c,c₁ - mecanism plan manivela-culisa oscilanta.

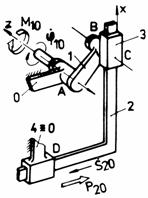
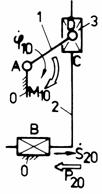
d d₁

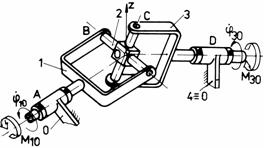
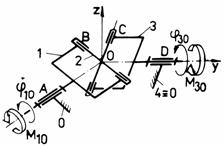
e e₁

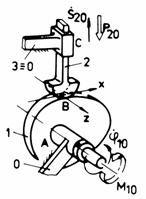
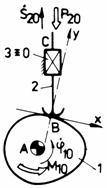
f f₁

Fig.  Tema de casa: d,d₁ - mecanismul plan manivela-culisor de tip sinus; e,e₁ - mecanism cardanic; f,f₁ - mecanism plan cu cama de rotatie si tachet de translatie.

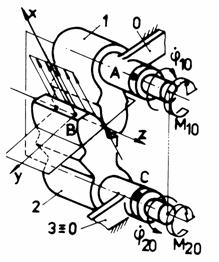
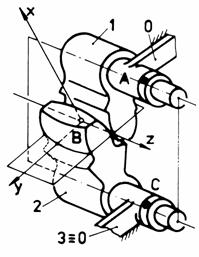
g

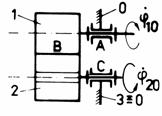
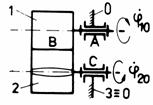
g

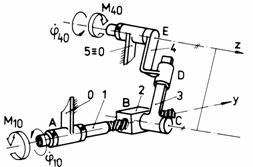
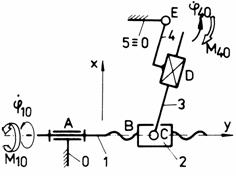
h h₁

Fig.  Tema de casa: g,g₁ - angrenaj cilindric cu dinti drepti (stanga) si angrenaj cilindric cu dinti bombati (dreapta); h,h₁ - mecanism cu surub de tip manivela-balansier.

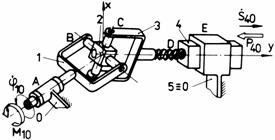
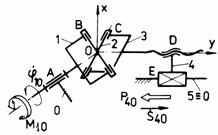
i i₁

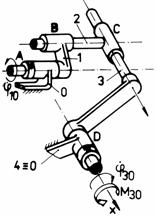
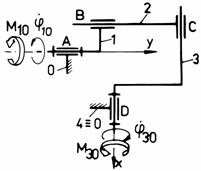
j j₁

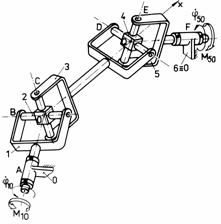
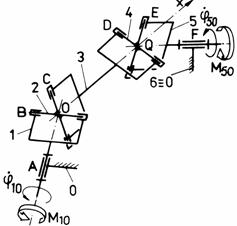
k k₁

Fig.  Tema de casa: i,i₁ - mecanism cu surub de tip manivela-culisor; j,j₁ - mecanism spatial de tip manivela-balansier (Altman); k,k₁ - mecanism bicardanic.