Drumuri in grafuri (I) (Networks - Shortest Route)

Drumuri in grafuri (I) (Networks - Shortest Route)

Se da un graf neorientat avand m noduri si n arce. Fiecare arc este caracterizat prin timpul sau costul parcurgerii lui sau prin distanta dintre extremitatile arcului.

Problema consta in determinarea drumului dintre doua noduri care are proprietatea de a minimiza o anumita masura a eficientei drumului, care este o functie de masurile atasate arcelor, de obicei suma lor.

Date de intrare:

numarul de arce [2 100]

pentru fiecare arc se indica:

numarul nodului de start;

numarul nodului final;

valoarea masurii arcului (timp, distanta, cost);

cele doua noduri pentru care se doreste determinarea drumului minim.

Exemplu:

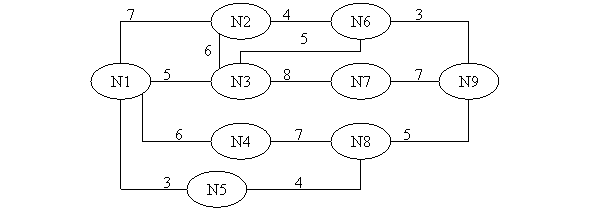Sa se determine drumul de lungime minima dintre punctele N1 si N9. Graful are 9 noduri: N1, N2, , N9 si 13 arce.

Rezolvare

Se introduc informatiile necesare celor 13 arce; de exemplu: - arcul 1 :(1, 2) corespunde perechii (N1, N2) si are valoarea 7.

Este indiferenta ordinea de introducere a informatiilor despre arce.

Solutia este data in pagina 59.

Observatii:

Graful fiind neorientat nu conteaza ordinea in care sunt indicate extremitatile arcelor.

Modulul permite determinarea drumului minim pentru orice pereche de noduri din graf.

Problema propusa:

Sa se determine drumurile de lungime minima dintre localitatea L1 si localitatile L8, L9, L10 si L11.

Sa se traseze graful asociat.

Sa se rezolve problema si sa se marcheze pe graf drumurile solutie obtinute.