Operatii cu grafuri

Operatii cu grafuri

Definitie: Suma carteziana a doua digrafuri G = ( N , A ) si G = ( N , A ) este notata G + G2 si este digraful G = ( N, A) definit astfel:

N = N N

A = .

Definitie: Produsul cartezian a doua digrafuri G = ( N , A ) si G = ( N , A ) este notat G G si este digraful G = ( N, A) definit astfel:

N = N N

A = .

Suma carteziana si produsul cartezian a doua grafuri simple neorientate

se definesc analog ca pentru doua digrafuri. De asemenea suma carteziana si produsul cartezian a p grafuri, p > 2, se definesc asemanator ca pentru doua grafuri.

Exemplu: Digraful reprezentat in figura 1.13(a) este suma carteziana a digrafurilor reprezentate in figura 1.12.

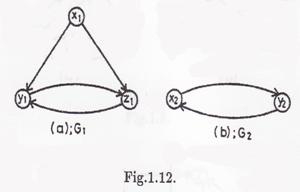
Arcul (x x , x y A deoarece x = x1 si (x , y A ; arcul (x x , y x A deoarece x = x si (x , y A etc. Digraful reprezentat in figura 1.13(b) este produsul cartezian al digrafurulor reprezentante in figura 1.12.

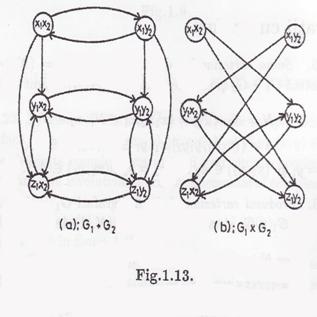
Arcul (x x , z y A deoarece (x ,z A si (x ,y A ; arcul (y y , z x A deoarece (y , z A si (y , x A etc.