REPREZENTARI GRAFICE IN TREI DIMENSIUNI

Reprezentari grafice in trei dimensiuni

1. Grafice de baza 3D

Pentru reprezentarea liniilor in spatiu se utilizeaza functia plot3, care se poate apela prin:

plot3(x,y,z - care reprezinta grafic o linie in spatiul 3D, linie care trece prin punctele ale caror coordonate sunt tripletele (x,y,z) si in care x, y si z sunt vectori de aceeasi dimensiune;

plot3(X,Y,Z), unde X, Y si Z sunt matrice de aceeasi dimensiune, reprezinta grafic cate o linie in spatiul 3D, pentru fiecare triplet al coloanelor matricelor [X(:,i), Y(:,i), Z(:,i)];

plot3(x,y,z, 'linie_tip' sau plot3(x1,y1,z1, 'linie_tip1', x2,y2,z2, 'linie_tip2',) - realizeaza reprezentari 3D multiple, in care se precizeaza tipurile de linii si culorile acestora, ca si in cazul functiei plot.

Reprezentarea unei spirale in 3D, figura 1, se poate face prin comenzile:

t=0:pi/50:10*pi; plot3(sin(t),cos(t),t); xlabel('sin(t)');ylabel('cos(t)'); zlabel('t').

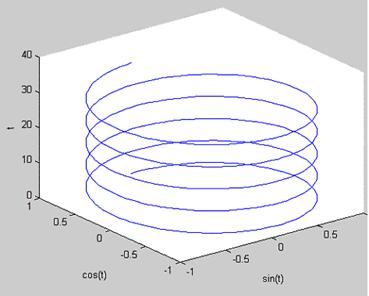
Fig. 1. Reprezentarea grafica a unei spirale cu functia plot3

Functia plot3 returneaza un vector coloana al identificatorilor de control al caracteristicilor obiectelor linie. Obiectele linie create cu plot3 sunt copii ai axelor curente. Tripletele (x,y,z) pot fi urmate de perechile parametru-valoare, pentru a specifica proprietatile suplimentare ale liniilor.

Pentru o citire mai precisa pe grafic, reprezentarea se poate asocia cu functia grid.

Reprezentarea grafica a suprafetelor 3D sub forma unei "retele" ("mesh") se face utilizand functia mesh.

Pentru reprezentarile grafice 3D ale suprafetelor si liniilor de contur se utilizeaza functiile meshc si meshz. Functia meshc reprezinta grafic combinatia suprafata 3D ("mesh") - linii de contur, reprezentate sub suprafata. Functia meshz reprezinta grafic suprafete 3D ("mesh"), cu plan de referinta la cota zero (piedestal).

In general, o suprafata este parametrizata prin doua variabile independente, i si j, care variaza continuu in interiorul unui dreptunghi. Daca, de exemplu 1≤i≤m si 1≤j≤n, atunci fiecare punct este specificat prin trei functii, X(i,j), X(i,j) si Z(i,j). Cand i si j sunt numere intregi, suprafata este definita in nodurile unei retele rectangulare (grid), iar matricele X, Y, Z, au dimensiunea mxn. Daca se doreste si precizarea culorii suprafetei, este necesara inca o matrice, C(i,j), de aceeasi dimensiune, mxn.

Fiecare punct al suprafetei rectangulare este conectat cu alte patru puncte vecine, astfel:

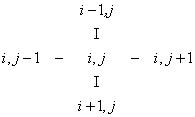
Punctele de pe margini sunt conectate cu trei noduri, iar colturile au numai doua noduri vecine.

In cazul general, functia mesh, meshc sau meshz se apeleaza cu patru matrice, ca parametrii de intrare, respectiv:

mesh(X,Y,Z,C),  meshc(X,Y,Z,C), meshz(X,Y,Z,C)

Pozitia din care este observata suprafata reprezentata grafic poate fi precizata cu functia view. Gradarea si etichetarea axelor este data de intervalele X,Y si Z sau de setarea curenta a axelor, prin functia axis. Culorile utilizate sunt cele determinate de C sau precizate prin functia caxis. Valorile scalei de culori sunt utilizate ca indici ai tabelei de culoare, din colormap.

In cazul in care matricea C este omisa, se considera C=Z, astfel incat culoarea este proportionala cu inaltimea suprafetei.

Daca apelarea se face,

mesh(x,y,Z,C),  meshc(x,y,Z,C), meshz(x,y,Z,C)

sau

mesh(x,y,Z),  meshc(x,y,Z), meshz(x,y,Z)

in care cele doua matrice sunt inlocuite de vectori, trebuie ca:

length(x)=n, length(y)=m si [m,n]=size(Z).

In acest caz, punctele retelei sunt specificate prin tripletul (x(j),y(i),Z(i,j)), unde x corespunde coloanelor lui Z, iar y corespunde randurilor. Pentru a rezulta o figura corecta, trebuie ca vectorii x si y sa fie ordonati crescator si cu pas constant.

Daca apelarea se executa,

mesh(Z),  meshc(Z), meshz(Z)

sau,

mesh(Z,C),  meshc(Z,C), meshz(Z,C)

atunci se considera x=1:n si y=1:m, iar reprezentarea se face pe baza indicilor matricei Z.

Apelate sub forma,

mesh(.,'NumeProprietate','ValoareProprietate',.), 

meshc(.,'NumeProprietate','ValoareProprietate',.), 

meshz(.,'NumeProprietate','ValoareProprietate',.), 

seteaza 'NumeProprietate' la 'ValoareProprietate' dorita, putand fi mai multe seturi de astfel de date intr-un singur segment.

Daca se apeleaza simplu mesh, meshc, meshz, atunci se returneaza un identificator spre obiectul suprafata.

Functiile axis, caxis, colormap, hold, shading, hiden si view seteaza proprietatile obiectelor figura, axe si suprafata, care afecteaza suprafetele "mesh" (retea) afisate.

O reprezentare a suprafetelor si a liniilor de contur, sub forma unei cascade, se poate face utilizand functia waterfall(X,Y,Z), care nu ploteaza coloanele retelei.

Pentru exemplificare, se considera functia Z=X.*exp(-X.^2-Y.^2), care se reprezinta in figura 2 astfel: a) cu functia mesh, ca o suprafata "mesh"; b) cu functia meshc, ca o suprafata "mesh" asociata cu linii de contur; c) cu functia meshz, ca o suprafata "mesh" cu plan de referinta; d) cu functia waterfall, ca o suprafata "mesh" sub forma de cascada.

Reprezentarea grafica a suprafetelor netede 3D se face cu functia surf, iar a suprafetelor 3D asociate cu linii de nivel proiectate pe planul bazei, cu functia surfc

Functia surf(X,Y,Z,C) reprezinta a suprafata descrisa de matricele X,Y si Z, si colorata cu elementele precizate in matricea C. In unele utilizari, argumentele X si Y pot fi vectori sau pot fi omise. De asemenea, matricea C poate fi omisa.

Punctul din care este vazuta o reprezentare 3D poate fi precizat prin functia view. Axele sunt date de matricele X,Y si Z sau setate cu functia axis. Culoarea este setata de matricea C sau prin functia caxis. Valorile scalate ale culorilor sunt indici la matricea de culoare curenta din colormap.

Culoarea suprafetei poate fi specificata prin doua metode diferite: specificand colturile retelei sau centrele acesteia. Nuantele sunt configurate cu functia shading. Daca functia shading este initializata la "interp", C trebuie sa aiba aceeasi dimensiune ca matricele X,Y,Z si specifica culorile colturilor, iar in interiorul zonei se realizeaza o interpolare lineara. Daca shading este initializata "faced" (valoare implicita) sau "flat", atunci C(i,j) specifica o culoare constanta in dreptunghiul respectiv.

Fig.2. Reprezentarea suprafetelor "mesh" 3D

Apelata ca surf(X,Y,Z), se considera C=Z, astfel incat culoarea este proportionala cu inaltimea suprafetei.

Functiile surf(x,y,Z) si surf(x,y,Z,C), avand ca argumente de intrare in locul celor doua matrice X si Y, vectorul x, de dimensiune n si vectorul y, de dimensiune m, cu conditia length(x)=n, length(y)=m, unde [m,n]=size(Z), iar matricea C are dimensiunea mxn.. In acest caz, colturile dreptunghiurilor care compun suprafata sunt tripletele (x(j),y(i),Z(i,j)). Prin urmare, x este asociat numarului de coloane, iar y numarului de linii.

Daca apelarea se face surf(Z) sau surf(Z,C), atunci se considera implicit x=1:n si y=1:m, pentru reprezentarea grafica 3D a matricei Z, folosind eventual si matricea de culoare C.

Specificarea unei anumite proprietati, Proprietate, si a valorii acesteia, Valoare, se realizeaza apeland functia sub forma, surf(,'Propietate','Valoare',), setul de proprietati si valori putand fi multiplicat de cate ori este necesar.

Functia surfc() este identica cu surf(), exceptand liniile de nivel, care sunt reprezentate sub suprafata, pe acelasi grafic.

Apelate simplu surf sau surfc se returneaza un identificator al obiectului suprafata, care este copil al obiectului axe.

Functiile axis, caxis, colormap, hold, shading si view seteaza proprietatile obiectelor figura, axe si suprafata, care afecteaza suprafetele afisate.

Pentru exemplificare, in figura 3 se prezinta o suprafata 3D redata: a) cu surf si b) cu surfc. Secventa Matlab utilizata a fost:

[X,Y]=meshgrid(-3:0.1:3);

Z=peaks(X,Y);

subplot(211); surf(X,Y,Z); subplot(212); surfc(X,Y,Z).

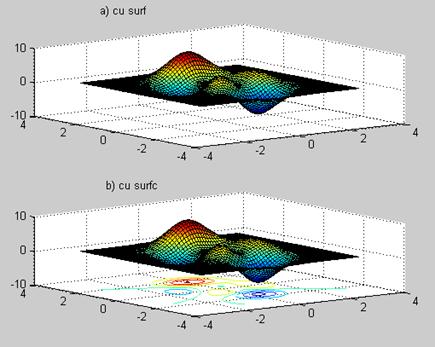
Fig.3. Reprezentarea 3D a suprafetelor cu surf si surfc

Reprezentarea grafica spatiala a poliedrelor se face cu functia fill3, care se apeleaza cu una dintre sintaxele:

fill3(x,y,z,c) - care reprezinta un poliedru 3D, avand varfurile definite de vectorii x,y si z, cu nuantele de culoare precizate de c, iar coordonatele poliedrului sunt specificate prin tripletele (x,y,z);

fill3(x,y,z, 'c') - care se deosebeste de precedenta prin aceea ca vectorul de culoare, c, are un singur caracter dintre cele prezentate in lista de culori de la functia plot, respectiv 'r','g','b', 'c','m','y','w','k', sau are trei componente [r g b], iar poliedrul va fi colorat cu o singura culoare;

fill3(x1,y1,z1, c1,x2,y2,z2,c2, ) - o forma mai usor de controlat pentru poliedre multiple, in care c1, c2, pot fi din lista de culori.

Daca c este un vector cu aceeasi lungime ca x si y, elementele acestuia sunt scalate cu functia caxis si apoi utilizate ca indici in matricea de culoare colormap, pentru a specifica culorile varfurilor. Culorile dintre varfuri sunt obtinute prin interpolare biliniara a culorilor varfurilor.

Daca x, y si z sunt matrice de aceeasi dimensiune, fill3(x,y,z,c) reprezinta cate un poliedru pentru fiecare coloana. In acest caz, c este un vector linie pentru poliedre reprezentate cu o singura culoare ("flat") si o matrice, pentru poliedre realizate cu culori interpolate, "interp" sau cu efecte speciale.

Daca numai unul dintre argumentele x, y sau z sunt matrice, celelalte fiind vectori coloana cu acelasi numar de linii, vectorii coloana se extind la matrice cu aceleasi dimensiuni, prin adaugarea unor coloane identice.

Functia fill3 returneaza un vector coloana al identificatorilor de control al modulelor obiect, cate o linie pentru fiecare modul.

Argumentele x, y, z si c pot fi urmate de perechile parametru-valoare, pentru a specifica proprietatile suplimentare ale modulului obiect.

Pentru exemplificare, se considera secventa:

x=1:100;y=x.^2.5;z=(x.*y);c=z;

subplot(211); fill3(x,y,z,'k'); subplot(212); fill3(x,y,z,c)

reprezentata in figura 4.

Fig.4. Reprezentarea grafica cu fill3

2. Reprezentarea conturului si grafice 2-1/2 D

Prin linii de contur se inteleg liniile situate la acelasi nivel pe axa Z (linii de nivel constant).

Calculul matricei C, care contine perechile de coordonate (X,Y) ale fiecarei linii de contur, matrice utilizata de functia contour, contour3 sau contourf, pentru a trasa conturul actual, se face cu functia contourc

Functia contourc se apeleaza cu una dintre sintaxele:

C=contourc(Z) - calculeaza matricea C a liniilor de contur ale matricei Z, alegand automat numarul liniilor de nivel si valorile acestora;

C=contourc(X,Y,Z) - calculeaza matricea C a liniilor de contur ale matricei Z si utilizeaza date din vectorii X si Y, pentru a scala axele Ox si Oy, iar elementele vectorilor X si Y sunt cu pas constant;

C=contourc(Z,n) sau C=contour(X,Y,Z,n)- calculeaza matricea C a liniilor de contur ale matricei Z, pentru n (scalar) linii de contur;

C=contourc(Z,v) sau C=contour(X,Y,Z,v)- calculeaza matricea C a liniilor de contur ale matricei Z la nivelurile specificate de vectorul v;

Matricea liniilor de contur, C, este o matrice cu doua linii, ca de exemplu:

C = [nivel1 x1 x2 x3 nivel2 x2 x2 x3 ;

perechi1 y1 y2 y3 perechi2 y2 y2 y3 ]

in care vectorii x si y trebuie sa fie monoton crescatori si cu pas constant.

Pentru suprafete nerectangulare sau parametrice calculul matricei C a liniilor de contur se face cu functia contours, care se apeleaza asemanator ca si functia contourc.

Reprezentarea grafica in plan a liniilor de contur se realizeaza cu functia contour, care se apeleaza cu una dintre sintaxele:

contour(Z) - reprezinta conturul liniilor de acelasi nivel ale matricei Z, cu precizarea: coltul din stanga sus al desenului corespunde elementului Z(1,1), iar numarul liniilor de contur si valorile cotelor Z sunt alese automat;

contour(X,Y,Z) - reprezinta conturul liniilor de acelasi nivel ale matricei Z, utilizand vectorul X pentru controlul scalarii pe axa Ox si vectorul Y pentru controlul scalarii pe axa Oy, iar numarul liniilor de contur si valorile cotelor Z sunt alese automat;

contour(Z,n) sau contour(X,Y,Z,n) - reprezinta conturul a n linii de nivel ale matricei Z, cu vectorii X si Y pentru controlul scalarii pe axa Ox si Oy, iar daca n lipseste, se considera valoarea implicita 10;

contour(Z,V) sau contour(X,Y,Z,V) - reprezinta conturul liniilor de nivel ale matricei Z, caracterizate de valorile specificate in vectorul V, cu vectorii X si Y pentru controlul scalarii pe axa Ox si Oy, iar daca V=[v v], se calculeaza un singur nivel;

contour(.,'tiplinie') - reprezinta liniile de contur cu liniile si culorile specificate de tiplinie;

C=contour(.) - returneaza matricea liniilor de contur C, descrisa la functia contourc si este utilizata de functia clabel;

[C,H]=contour(.) - returneaza matricea liniilor de contur C si un vector coloana H, al identificatorilor obiectelor linie.

De mentionat ca matricea Z trebuie sa aiba cel putin dimensiunea 3.

Pentru exemplificare, in figura 5 se reprezinta grafic conturul liniilor de nivel ale functiei z=exp(-x²-y²) in domeniul -2≤x≤2, -2≤x≤3, obtinute prin rularea secventei Matlab:

[x,y]=meshgrid(-2:0.2:2, -2:0.2:3);

z=x.*exp(-x.^2-y.^2);

contour(-2:0.2:2, -2:0.2:3,z,8);

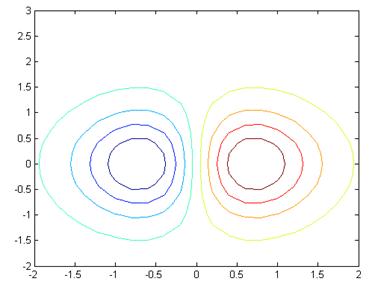
Fig.5. Reprezentarea grafica a liniilor de contur cu functia contour

Etichetarea cotelor liniilor de contur intr-o reprezentare grafica se face cu functia clabel, care se poate apela cu una dintre sintaxele:

clabel(C) - eticheteaza liniile de nivel, iar pozitia acestora este aleasa aleator;

clabel(C,H,V) - eticheteaza liniile de nivel numai pentru valorile V sau toate, daca V lipseste, unde C si H sunt respectiv, matricea liniilor de contur si identificatorul obiectelor linie, rezultate ca marimi de iesire ale functiilor contour, contour3 sau contourf, selectand aleatoriu pozitia etichetelor;

clabel(C,, 'manual') - eticheteaza liniile de nivel selectate cu mouse-ul, apasand tasta "ENTER", pentru a termina actiunea si "Space Bar", pentru a introduce urmatoarea linie de nivel;

clabel 'proprietate_text', valoare_proprietate, ) - precizeaza valorile, valoare_proprietate, unei proprietati a textului, proprietate_text, precum dimensiune font (fontsize), culoare font (color), rotatie text (rotation), spatierea (labelspacing), care are valoarea implicita 144 puncte.

Pentru exemplificare, se considera aceeasi functie ca mai sus si urmatoarele secvente Matlab:

[x,y]=meshgrid(-2:0.4:2, -2:0.5:3); z=x.*exp(-x.^2-y.^2);

subplot(1,3,1); [cs,h]=contour(-2:0.4:2,-2:0.5:3,z);clabel(cs,h,'labelspacing',72)

subplot(1,3,2); cs=contour(-2:0.4:2,-2:0.5:3,z);clabel(cs); subplot(1,3,3);

[cs,h]=contour(-2:0.4:2,-2:0.5:3,z);clabel(cs,h,'fontsize',12,'color','r','rotation',0)

prezentate in figura 6.

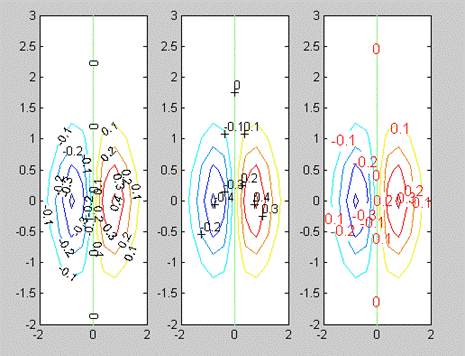
Fig.6. Etichetarea liniilor de contur cu functia clabel

Reprezentarea grafica in plan a liniilor de contur pline (filled) se realizeaza cu functia contourf, care se apeleaza asemanator ca functia contour. Zonele dintre liniile de contur sunt colorate diferit, cum sunt prezentate frecvent hartile termice. Un exemplu de utilizare este redat in figura 7, realizat cu secventa de instructiuni:

z=peaks; contourf(z), hold on, shading flat

[c,h]=contour(z,'k-'); clabel(c,h), colorbar

Reprezentarea grafica in spatiu a liniilor de nivel constant se realizeaza cu functia contour3, care se apeleaza ca si functia contour. Un exemplu este prezentat in figura 8, realizat cu instructiunea contour3 (peaks).

Fig.7. Reprezentarea grafica a liniilor de contur cu functia contourf

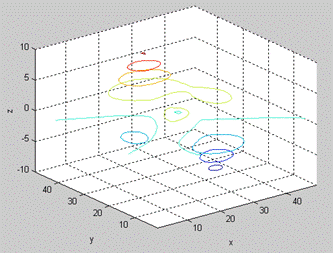
Fig.8. Reprezentarea grafica in spatiu a liniilor de nivel cu functia contour3

Pentru plotarea facila a conturului unei expresii introduse direct ca argument (de genul functiei humps) se utilizeaza functia ezcontour, care se poate apela:

ezcontour(f) - ploteaza liniile de contur ale functiei f(x,y), utilizand functia contour, unde f este un semn (de functie) sau o expresie simbolica, reprezentand o functie matematica de doua variabile, x si y, considerand domeniul implicit -2*pi < x < 2*pi, -2*pi < y < 2*pi si acordand corespunzator gridul;

ezcontour(f, Dom) - ploteaza f pe domeniu, Dom, care poate fi un vector de doua dimensiuni, [a b], respectiv (a < x < b, a < y < b), de 4 dimensiuni, [xmin xmax ymin ymax] sau [xmin xmax], [ymin ymax], respectiv (xmin < x < xmax, ymin < y < ymax) sau valoarea implicita, 2*pi < x < 2*pi, -2*pi < y < 2*pi ;

ezcontour(, N) - ploteaza f pe domeniul implicit considerand un grid NxN, in care valoarea implicita a lui N=60.

Pentru rotirea unui grafic 3D se utilizeaza rotate3d sau se clicheaza semnul rotire de pe figura graficului si se manevreaza cu mouse-ul.

Reprezentarea grafica usoara in plan, a liniilor de contur pline (filled) se realizeaza cu functia ezcontourf, care se apeleaza asemanator cu functia ezcontour. Zonele dintre liniile de contur sunt colorate diferit.

3. Alte grafice 3D

Reprezentarea grafica 3D sub forma de bare veticale se realizeaza cu functia bar3, care se poate apela cu sintaxa:

bar3(Y,Z - reprezinta coloanele matricei Z, de mxn, prin bare verticale in 3D de inaltime data de length(Z);Y este un vector monoton crescator sau descrescator, iar culoarea este setata prin colormap;

bar3(Z - este asemanatoare ca bar3(X,Z), cu deosebirea ca utilizeaza pentru y valoarea implicita Y=1:m;

bar3(Y,Z,gros) sau bar3(Z,gros) - specifica grosimea barei date de gros, care poate lipsi si atunci, valoarea implicita este gros=0.8, daca gros<0.8 barele au grosimea data de gros, iar daca gros>1 atunci barele se unesc;

bar3(. 'detached') - este valoarea implicita si reprezinta barele detasate pe seturi de date;

bar3(. 'grouped') - reprezinta barele grupate pe seturi de date si cu aceeasi culoare;

bar3(. 'stacked') - reprezinta barele sectionate cu culori diferite pentru seturile de date;

bar3(. 'culoarelinie') - reprezinta barele cu culori specificate din tab.1, respectiv una dintre 'r g b y m c k w'.

Apelata simplu, bar3, functia returneaza si date despre suprafata.

Pentru exemplificare, se prezinta figura 9, realizata cu secventa:

subplot(1,2,1), bar3(peaks(5)); subplot(1,2,2), bar3(rand(5),'stacked').

Reprezentarea barelor 3D orizontale se realizeaza cu functia bar3h, care este asemanatoare functiei bar3. Pentru exemplificare, se considera secventa anterioara, in care se inlocuieste bar cu barh, reprezentata in figura 10.

Returnarea valorilor initiale utilizate se realizeaza cu functia makebars.

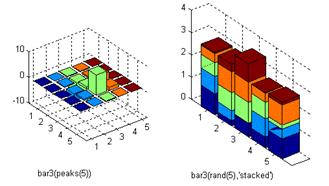
Fig.9. Reprezentarea grafica cu bar3

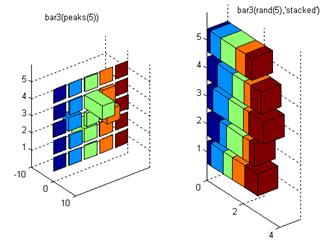
Fig.10. Reprezentarea grafica cu bar3h

Reprezentarea grafica a unui punct, care urmareste realizarea grafica spatiala ("cometa"), se executa cu functia comet3, care se apeleaza cu una dintre sintaxele:

comet3(z) - reprezinta vectorul z intr-un grafic tridimensional, animat, prin urmarirea de un marker ("cometa), la o distanta de 0.1 din lungimea vectorului z;

comet3(x,y,z) - reprezinta curba data prin punctele (x(i),y(i),z(i)), in mod animat, prin urmarirea de un marker ("cometa), la o distanta de 0.1 din lungimea vectorului z;

comet3(x,y,z,p) - la fel ca precedenta, dar distanta de urmarire este setata la valoarea p din lungimea totala a vectorului z.

Pentru exemplificarea modului de lucru, se recomanda exemplul:

t = -pi:pi/500:pi;

comet3(sin(5*t),cos(3*t),t).

Pentru plotarea facila 3D se utilizeaza functia ezplot3, care se poate apela:

ezplot3(x,y,z) - pentru plotarea in spatiu a curbei x = x(t), y = y(t), z = z(t), care considera implicit, pentru t, domeniul 2*pi < t < 2*pi;

ezplot3(x,y,z,[tmin, tmax]) - pentru plotarea in spatiu a curbei x =x (t), y = y(t), z = z(t), care considera pentru t domeniul tmin < t < tmax;

ezplot3(x,y,z, 'animate') sau ezplot3(x,y,z,[tmin, tmax], 'animate') - la fel ca si cele anterioare, dar produce o curba spatiala animata, de genul "comet".

De mentionat ca x, y si z pot fi functii definite inline @, sau expresii, ca in exemplul:

fy = inline('t .* sin(t)') ; ezplot3(@cos, fy, @sqrt)

ezplot3('cos(t)', 't * sin(t)', 'sqrt(t)', [0,6*pi])

ezplot3(@cos, fy, @sqrt, 'animate')

redat in figura 11.

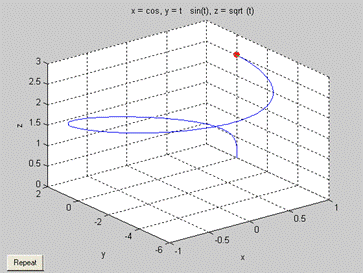
Fig.11. Reprezentarea grafica cu ezplot3

Reprezentarea grafica a unei suprafete discrete Z, sub forma unor plane xy, terminate cu cerc, se executa cu functia stem3, care se apeleaza cu una dintre sintaxele:

stem3(Z) - traseaza suprafata discreta Z sub forma unor plane xy, terminate cu cerc;

stem3(X,Y,Z) - traseaza suprafata Z la valorile specificate de X si Y;

stem3(x,y,linie_tip) sau stem3(x,y, 'filled') - traseaza un grafic linii de tipul si culoarea precizata in sirul de caractere linie_tip, similar cu functia plot, ca de exemplu stem3(x,y,':r'), sau stem3(x,y, 'filled'), cand cercurile sunt umplute (colorate).

Plotarea dispersiei vectorilor in 3D, la locatiile specificate de vectorii X, Y, Z (care trebuie sa fie de aceeasi dimensiune), cu markere (cercuri implicit) de arie determinata de valorile vectorului S ,(in puncte^2) si fiecare punct colorat, conform valorilor vectorului C, se face cu scatter3(X,Y,Z,S,C). Daca S este scalar, atunci fiecare marker va avea aceeasi dimensiune. Cand C este un vector de aceeasi lungime ca si X, Y si Z, valorile lui C sunt interpolate linear intre culorile curente din colormap. Daca C este o matrice de 3 dimensiuni, culorile markerelor au valori RGB. De asemenea, C poate fi specificat cu culori din tabelul 17.1, respectiv una dintre 'r g b y m c k w'.

Functia scatter3(X,Y,Z) traseaza markere de culori si dimensiuni implicite, scatter3(X,Y,Z,S) traseaza markere cu o singura culoare, iar prin scatter3(,'filled') cercurile sunt umplute (colorate total).

Returnarea indicatorilor de control se face prin apelarea functiei scatter3.

Un exemplu de utilizare este dat in figura 12, obtinut cu secventa:

[x,y,z] = sphere(16);

X = [x(:)*.5 x(:)*.75 x(:)]; Y = [y(:)*.5 y(:)*.75 y(:)];

Z = [z(:)*.5 z(:)*.75 z(:)]; S = repmat([1 .75 .5]*10,prod(size(x)),1);

C = repmat([1 2 3],prod(size(x)),1);

scatter3(X(:),Y(:),Z(:),S(:),C(:),'filled'), view(-60,60).

Fig.12. Reprezentarea grafica cu scatter3

Realizarea unei diagrame 3D circulare (asa numita diagrama "placinta") cu valorile unui vector X, avand specificate semnificatia in eticheta, se face cu functia pie3(X,eticheta), apelata:

pie3

si rezultand diagrama din figura 13.

De mentionat ca valorile lui X sunt normalizate, iar daca sum(X)<1, atunci sunt trecute valorile efective si apare un segment de cerc.

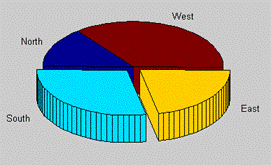
Fig.13. Reprezentarea grafica cu pie3

Pentru plotarea facila a retelei (gridului) unei expresii introduse direct ca argument (de genul functiei humps), se utilizeaza functia ezmesh, care se poate apela:

ezmesh(f) - ploteaza graficul functiei f(x,y) utilizand functia mesh, unde f este un semn sau o expresie simbolica, reprezentand o functie matematica de doua variabile, ca x si y, considerand domeniul implicit -2*pi < x < 2*pi, -2*pi < y < 2*pi si acordand corespunzator gridul;

ezmesh(f, Dom) - ploteaza f pe domeniu, Dom, care poate fi un vector de doua dimensiuni, [a b], respectiv (a < x < b, a < y < b), de 4 dimensiuni, [xmin xmax ymin ymax] ori [xmin xmax], [ymin ymax], respectiv (xmin < x < xmax, ymin < y < ymax) sau valoarea implicita, 2*pi < x < 2*pi, -2*pi < y < 2*pi ;

ezmesh(, N) - ploteaza f pe domeniul implicit, considerand un grid NxN, in care valoarea implicita a lui N este 60;

ezmesh(,'circ') - ploteaza f pe un disc, centrat pe domeniul considerat.

Posibilitatile de apelare a functiei ezmesh sunt:

f = ['3*(1-x)^2*exp(-(x^2) - (y+1)^2)'

'- 10*(x/5 - x^3 - y^5)*exp(-x^2-y^2)'

'- 1/3*exp(-(x+1)^2 - y^2)'];

ezmesh(f,[-pi,pi])

ezmesh('x*exp(-x^2 - y^2)'); ezmesh('x*y','circ');

ezmesh('real(atan(x + i*y))'); ezmesh('exp(-x)*cos(t)',[-4*pi,4*pi,-2,2]);

ezmesh('s*cos(t)','s*sin(t)','t');

ezmesh('exp(-s)*cos(t)','exp(-s)*sin(t)','t',[0,8,0,4*pi]);

ezmesh('(s-sin(s))*cos(t)','(1-cos(s))*sin(t)','s',[-2*pi,2*pi]);

h = inline('x*y - x'); ezmesh(h); ezmesh(@peaks)

Pentru plotarea facila a retelei si a liniilor de contur ale unei expresii introduse direct ca argument, se utilizeaza functia ezmeshc, care se apeleaza asemanator cu functia ezmesh.

Pentru plotarea facila a suprafetelor colorate a unei expresii introduse direct ca argument, se utilizeaza functia ezsurf, care se apeleaza ca si ezmesh. Suprafetele sunt date parametric, x = x(s,t), y = y(s,t), z = z(s,t), ca de exemplu:

ezsurf('(1-s)*(3+cos(t))*cos(4*pi*s)', .

'(1-s)*(3+cos(t))*sin(4*pi*s)',

'3*s + (1 - s)*sin(t)', [0,2*pi/3,0,12] )

exemplificata in figura 14.

Pentru plotarea facila a suprafetelor colorate combinate, cu trasarea liniilor de contur a unei expresii introduse direct ca argument, se utilizeaza functia ezsurfc, care se apeleaza ca si ezmesh sau ezsurf, ca in figura 15, realizata cu comanda:

ezsurfc('(s-sin(s))*cos(t)','(1-cos(s))*sin(t)','s',[-2*pi,2*pi]).

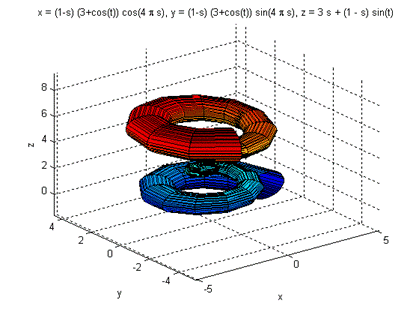
Fig.14. Reprezentarea grafica cu ezsurf

Pentru plotarea facila 3D a unei expresii introduse direct ca argument (de genul functiei humps) se face usor cu functia ezgraph3, care se poate apela:

ezgraph3(Plotfun,f) - ploteaza z=f(x,y), utilizand pentru plotare functia Plotfun, care poate fi o functie oarecare, ca de exemplu surf, avand ca argumente de intrare (x,y,z);

ezgraph3(Plotfun,f, [xmin xmax ymin ymax]) - ploteaza pe domeniul specificat, [xmin xmax ymin ymax];

ezgraph3(Plotfun,x,y,z, [smin smax tmin tmax])) - ploteaza pe domeniul specificat, [smin smax tmin tmax];

ezgraph3(x,y,z, [a b])) - ploteaza pe domeniul specificat, [a b];

ezgraph3(Plotfun,,Domstyle) - in care Domstyle poate fi 'rect' sau 'circ';

ezgraph3(Plotfun,,Npts) - utilizeaza un grid de NxN puncte;

ezgraph3(Plotfun,x,y,z) - ploteaza suprafata parametrica x=x(s,t), y=y(s,t) si z=z(s,t) pe domeniul -2*pi < s < 2*pi and -2*pi < t < 2*pi.

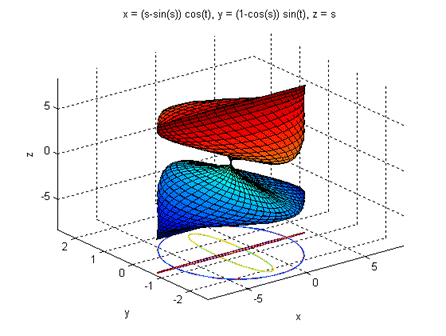
Fig.15. Reprezentarea grafica cu ezsurfc

Plotarea unor suprafete triunghiulare colorate definita de matricea TRI, de dimensiuni Mx3, se realizeaza cu functia trisurf, care se apeleaza cu una dintre sintaxele:

trisurf(TRI,X,Y,Z,C) - ploteaza triunghiurile definite de matricea TRI, de dimensiuni Mx3 ; randurile lui TRI contin indicii vectorilor X,Y si Z care definesc o singura fata a triunghiului, iar C este vectorul culoare;

trisurf(TRI,X,Y,Z) - utilizeaza C=Z, adica vectorul culoare este proportional cu inaltimea Z;

trisurf( 'param','val',.) - defineste un parametru, param, cu o anumita valoare, val;

h=trisurf(.) - returneaza vectorul h, al identificatorilor obiectelor.

Un exemplu de utilizare este redat in figura 16, realizat cu secventa Matlab:

[x,y]=meshgrid(1:15,1:15);

tri = delaunay(x,y);

z = peaks(15);

trisurf(tri,x,y,z).

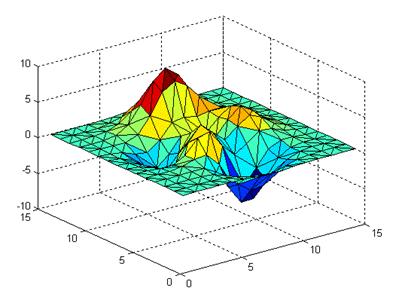
Fig.16. Reprezentarea grafica cu trisurf

Plotarea unor panglici 3D se realizeaza cu functia ribbon, care se apeleaza ca si ribbon.

De mentionat ca interiorul suprafetelor triunghiulare nu este colorat.

ribbon(X,Y,gros) - ploteaza coloanele Y separat, ca panglici 3D, in care gros este grosimea panglicii (valoarea implicita este gros=0.75), iar daca X lipseste, se considera X=1:size(Y,1);

h=ribbon(.)- returneaza vectorul h, al identificatorilor obiectelor.

Un exemplu de aplicare este dat in figura 17, realizata cu secventa:

X=1:10;Y=X.^2;gros=0.5;ribbon(X,Y,gros).

Fig.17. Reprezentarea grafica cu ribbon

4. Reprezentarea obiectelor spatiale solide

Reprezentarea grafica a obiectului cilindru se face cu functia cylinder, care genereaza un cilindru de raza R, cu cercul bazei aproximat din N puncte echidistante si care se apeleaza cu sintaxa:

[X,Y,Z]=cylinder(R,N),

in care, daca N lipseste, se considera valoarea implicita N=20, iar daca R lipseste, se considera valoarea implicita R=[1 1].

Functia returneaza matricele X, Y, Z cu 2x(N+1) elemente, care specifica varfurile fiecarei suprafete rezultate din aproximarea cercurilor bazelor cu poligoane cu n laturi. Reprezentarea grafica se face cu functia surf(X,Y,Z). Omiterea argumentelor de iesire determina automat reprezentarea grafica a obiectului cilindru.

Vectorul R are in mod normal 2 elemente, R=[R1 R2], care precizeaza raza obiectului, la partea inferioara (R1) si superioara (R2), ceea ce face posibila construirea de conuri, trunchiuri de con, piramide, trunchiuri de piramida.

Pentru exemplificare, in figura 18 se prezinta diverse posibilitati de utilizare a functiei cylinder, considerand secventa Matlab:

Rc1=1;Rc2=0;Rc3=0.5;Hc1=10;Hc2=8;N1=40;N2=6;

[xc,yc,zc]=cylinder([Rc1 Rc1],N1);zc=zc.*Hc1;

subplot(221);surf(xc,yc,zc,xc)

[xcon,ycon,zcon]=cylinder([Rc1 Rc2],N1);zcon=zcon.*Hc1;

subplot(222);surf(xcon,ycon,zcon,xcon)

[xp,yp,zp]=cylinder([Rc1 Rc2],N2);zp=zp.*Hc1;

subplot(223);surf(xp,yp,zp,xp)

[xtp,ytp,ztp]=cylinder([Rc1 Rc3],N2);ztp=ztp.*Hc2;

subplot(224);surf(xtp,ytp,ztp,xtp).

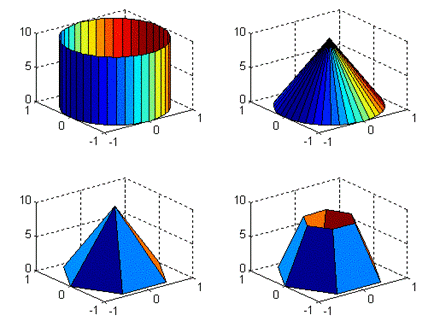
Fig. Reprezentarea grafica cu cylinder

Reprezentarea grafica a obiectului sfera utilizeaza functia sphere, care genereaza coordonatele (X, Y, Z) ale sferei unitate, utilizate de functiile surf sau mesh pentru reprezentare grafica. Coordonatele X, Y si Z sunt matrice de (N+1)x(N+1), unde N este numarul de puncte echidistante folosite pentru reprezentare, avand valoarea implicita N=20 (daca N lipseste).

Apelarea se face cu sintaxa:

[X,Y,Z]=sphere(N).

Omiterea argumentelor de iesire determina automat reprezentarea grafica a obiectului sfera.

Pentru exemplificare, se considera figura 19, care reprezinta sfera generata prin secventa:

[X,Y,Z]=sphere(25); surf(X,Y,Z).

Daca s-ar fi utilizat mesh, atunci segmentele (fasiile) nu ar fi fost colorate.

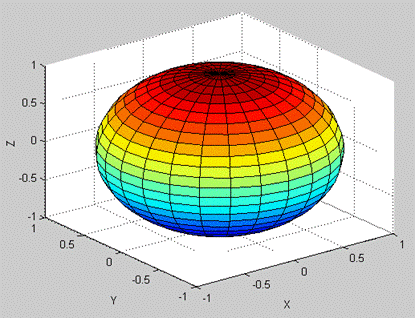
Fig.19. Reprezentarea grafica cu sphere

Pentru generarea unui elipsoid se utilizeaza functia ellipsoid, care se apeleaza cu sintaxa:

[X,Y,Z]=ellipsoid(XC,YC,ZC,XR,YR,ZR,N) prin care se genereaza matricele (X, Y, Z) de (N+1)x(N+1), utilizate de functia surf cu comanda surf(X,Y,Z), pentru a produce un elipsoid avand centrul (XC, YC, ZC) si razele XR, YR, ZR; N este numarul de puncte utilizate la reprezentare (valoarea implicita N=20);

ellipsoid() sau ellipsoid(,N), deci fara argumente de iesire, ploteaza elipsoidul apeland la functia surface.

Ecuatia elipsoidului este

5. Vizualizarea volumelor si a vectorilor

Pentru vizualizarea volumelor si a vectorilor sunt disponibile, in Matlab, o serie de facilitati specifice, ce se pot apela prin help-ul vissuite. Astfel,

pentru date scalare:

isosurface - extrage o izosuprafata;

isonormals - normalele la izosuprafata;

isocaps - izosuprafetele la capete;

contourslice - traseaza conturul in planurile de separatie;

isocolors - coloreaza fiecare fasie de izosuprafata;

pentru date vectoriale:

streamline - linii de curent pentru vectori 2D sau 3D;

stream2  - linii de curent 2D;

stream3  - linii de curent 3D;

divergence - divergenta unui camp de vectori 2D sau 3D;

curl - viteza tangentiala si normala;

coneplot - ploteaza vectorii viteza sub forma 3D;

quiver - reprezinta grafic campuri de vectori orientati in 2D;

quiver3 - reprezinta grafic campuri de vectori orientati in 3D;

streamtube - traseaza tuburi de curent 3D;

streamribbon - traseaza tuburi de curent 3D sub forma de panglici;

streamslice - linii de curent orientate;

streamparticles - linii de curent pe care se misca particule;

interpstreamspeed - interpoleaza liniile de curent cu viteza;

slice - ploteaza felii volumetrice;

utilitare:

subvolume  - extrage un set de date din volumul de date initial;

reducevolume - reduce volumul de date;

volumebounds - returneaza datele volumului x, y, z si limitele culorilor;

smooth3  - niveleaza datele 3D;

reducepatch - reduce numarul de volume de discretizare;

shrinkfaces - reduce numarul de suprafete de discretizare;

surf2patch - converteste datele de suprafata in date de volume de discretizare.

Pentru exemplificare, se prezinta functia quiver, care permite reprezentarea grafica a unui camp de vectori orientati. Apelarea se face cu una dintre sintaxele:

quiver(X,Y,U,V) - reprezinta mici segmente de dreapta cu sageti (vectori), avand originea la perechile de elemente (X, Y), iar U si V sunt proiectiile vectorului pe axele Ox si Oy, cu mentiunea ca matricele X, Y, U, V trebuie sa aiba aceeasi dimensiune;

quiver(U,V) - considera implicit X=1:n si Y=1:m, iar U si V sunt pe o retea rectangulara;

quiver(X,Y,U,V,S) sau quiver(U,V,S) - controleaza lungimea sagetilor prin factorul de scala S, care daca lipseste sau S=0, se face automat;

Se pot specifica tipurile de linii si culorile la fel ca pentru functia plot

Pentru exemplificare, se prezinta in figura 20 un camp de vectori realizat cu secventa:

[x,y] = meshgrid(-2:.2:2,-1:.15:1);

z = x .* exp(-x.^2 - y.^2); [px,py] = gradient(z,.2,.15);

contour(x,y,z), hold on; quiver(x,y,px,py), hold off, axis image.

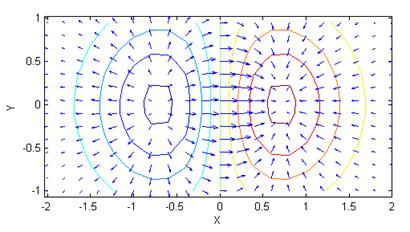
Fig.20. Reprezentarea unui camp de vectori cu functia quiver

6. Pozitionarea observatorului fata de obiect

Definirea pozitiei observatorului fata de un obiect 3D se face cu functia view, care precizeaza unghiul pe orizontala (numit azimut) si unghiul pe verticala (numit elevatie).

Functia view este utilizata pentru vizualizarea unei reprezentari grafice spatiale din diverse pozitii si se apeleaza cu una dintre sintaxele:

view(az,el) sau view([az,el]) - stabileste unghiul din care se vede reprezentarea grafica 3D, unde az este azimutul (unghiul in plan orizontal), iar el este elevatia (unghiul pe verticala); ambele unghiuri sunt date in grade;

view([x,y,z]) - stabileste unghiul punctului de observare in coordonate carteziene, ignorand magnitudinea vectorilor x, y, z;

view(2) - stabileste reprezentarea grafica la 2D, cu valorile implicite az=0 si el=90;

view(3) - stabileste reprezentarea grafica 3D, cu valorile implicite az=-37.5 si el=30;

[az,el]=view - returneaza unghiul pe orizontala, azimutul az si unghiul pe verticala, elevatia el, din care este observata o reprezentare grafica 3D.

De mentionat ca, azimutul, az, poate lua valori pozitive sau negative, cea pozitiva fiind o rotire in jurul axei Oz ,in sens orar. Valorile pozitive ale elevatiei, el, corespund unui punct de observare plasat deasupra planului (x,y), iar valorile negative corespund punctelor de sub plan.

Valorile caracteristice ale azimutului sunt:

az=-37.5, el=30 - valori implicite, care conduc la reprezentarea 3D;

az= 0, el=90 - valori ce conduc la reprezentarea 2D;

az= 0, el=0 - conduc la vederea directa din planul zero;

az= 180, el=elevat - vedere din spate a obiectului la o elevatie, elevat, dorita.

In figura 21 sunt exemplificate aceste valori, utilizand reprezentarea trunchiului de piramida din figura 18 si secventa de program:

subplot(221); surf(xtp,ytp,ztp,xtp); view(-37.5,30); subplot(222);

surf(xtp,ytp,ztp,xtp);view(0,90); subplot(223); surf(xtp,ytp,ztp,xtp);

view(0,0); subplot(224); surf(xtp,ytp,ztp,xtp); view(180,30).

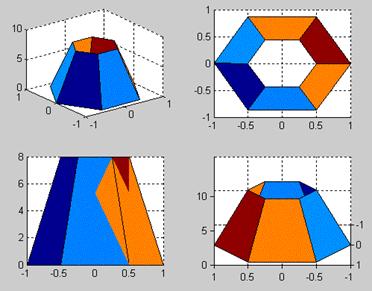
Fig.21. Vederea unei figuri cu view

Returnarea matricei de transformare ortogonala, cu dimensiunea 4x4, utilizata la proiectia vectorilor spatiali 3D pe suprafata 2D, se face utilizand functia viewmtx, care se apeleaza cu sintaxa:

A=viewmtx(az,el,phi),

unde: A - matricea de transformare; az - azimutul; el - elevatia; phi - unghiul de vizualizare si control al distorsiunilor, relativ la un cub normalizat.

Rotirea unei figuri 3D pentru vizualizare cu ajutorul mouse-ului se face cu functia rotate3d, care se apeleaza cu sintaxa:

rotate3d on - cand rotirea este permisa;

rotate3d off - cand nu mai este permisa rotirea.