Stucturi de date utilizate in reprezentarea grafurilor

Stucturi de date utilizate in reprezentarea grafurilor

Performanta unui algoritm utilizat pentru rezolvarea unei probleme din teoria grafurilor depinde nu numai de stuctura algoritmului utilizat ci si de modul de reprezentare in calculator a topologiei grafului.

Fie un digraf G = ( N, A) cu N = si A = . Se considera functia valoare b : A si functia capacitate c : A . Functia valoare b reprezinta fie functia lungime, fie functia cost etc. Functiile b, c se pot defini si pe multimea nodurilor.

Definitie: Un digraf G = ( N, A) pe care s-a / s-au definit functia b sau / si functia c se numeste retea orientata si se noteaza fie G = ( N, A, b), fie G = ( N, A, c), respectiv G = ( N, A, b, c).

Analog se defineste o retea neorientata.

In acest paragraf se vor prezenta cele mai uzuale structuri de date utilizate pentru reprezentarea retelelor. Pentru reprezentarea unei retele este necesar, in general, sa memoram doua tipuri de informatii:

a) informatii privind topologia retelei;

b) informatii privind functia b sau/ si functia c.

In acest paragraf se prezinta reprezentarile retelelor orientate. Reprezentarile corespunzatoare retelelor neorientate sunt similare cu reprezentarile retelelor orientate. La sfarsitul acestui paragraf sunt prezentate pe scurt si reprezentarile retelelor neorientate.

Reprezentarea prin matricea de adiacenta consta in memorarea matricei de adiacenta M = ( mi j n n , unde

Daca este necesar sa memoram functia b sau / si functia c, atunci memoram matricea valoare B = ( bi j n n , unde

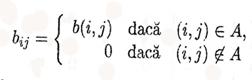
sau / si matricea capacitate C = ( ci j n n , unde

Reprezentarea prin matricea de incidenta consta in memorarea matricei de incidenta = ( i j n m , unde

Exemplu: Consideram reteaua orientata din figura 1.14.

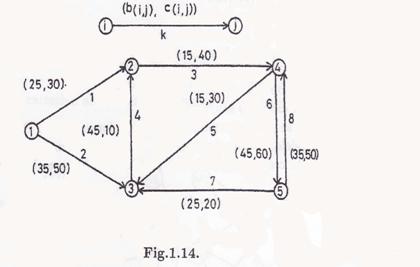
Matricele M, B, C, sunt urmatoarele :

, , ,

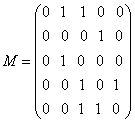Matricele M, B, C au fiecare n² elemente si numai m elemente nenule. Matricea are nm elemente si numai 2m elemente nenule (pe fiecare coloana cate 2 elemente nenule, un 1 si un -1). Rezulta ca reprezentarea prin matrice associate retelei este eficienta numai in cazul retelelor dense (m>>n). Pentru retele rare (m<< n² ) este efficient sa utilizam liste de adiacenta sau liste de incidenta.

Lista nodurilor adiacente catre exterior nodului i este V (i) = si lista arcelor incidente catre exterior nodului i este E (i) = .

Consideram ca listele V (i) si E (i) sunt ordonate, si avem |V (i)| =

| E (i) | = (i) , i = 1,..,n.

Reprezentarea prin liste de adiacenta poate fi utilizata in una din urmatoarele doua variante:

à reprezentarea cu ajutorul tablourilor;

à reprezentarea cu ajutorul listelor simplu inlantuite.

Reprezentarea cu ajutorul tablourilor consta in a defini doua tablouri unidimensionale. Primul tablou, notat P, are n+1 elemente si reprezinta o lista de pointeri. Tabloul P se defineste astfel : P(1) = 1, P(i+1) = P(i) + (i)

, i = 1,.., n. Al doilea tablou, notat V, are m elemente si reprezinta o lista de noduri. Tabloul V contine nodurile j din lista V (i), in ordinea stabilita, intre locatiile P(i) si P(i+1) - 1 , i = 1,., n.

Reprezentarea cu ajutorul tablourilor poate fi realizata si prin utilizarea unui tablou bidimensional

unde p = n + m. Elementele T(1, k) , k = 1,., p sunt noduri si elementele T(2, k) , k = 1,., p sunt pointeri. Prima linie a tabloului T se defineste astfel :

Elementul T(1, k) reprezinta :

à nodul k , daca 1kn

à un nod j din , daca n + P(i) k n + P(i+1), i = 1,., n.

A doua linie a tabloului T se defineste astfel:

Elementul T(2, k)0 reprezinta adresa (coloana) din T(1, k ), adica k =T(2, k) :

à a primului nod j din , daca 1 k n

à a urmatorului nod j ′ a lui j =T(1, k) din , daca n + P(i) k < n + P(i + 1) - 1, i = 1,., n.

Reprezentarea cu ajutorul listelor simplu inlantuite consta din n liste, fiecare lista corespunde la un nod i si are locatii. Fiecare locatie corespunde unui arc (i, j) si contine mai multe campuri: un camp pentru memorarea nodului j, un camp pentru memorarea pointerului care indica legatura la urmatoarea locatie si eventual un camp sau doua campuri pentru b(i, j) sau / si c(i, j). Daca locatia este ultima din lista inlantuita atunci prin conventie in campul pointerului punem valoarea 0. Deoarece avem n liste, una pentru fiecare nod i cu locatii, este necesar un tablou unidimensional, notat CAP, cu n elemente ce contine pointeri care indica prima locatie din fiecare lista inlantuita. Daca = 0 atunci CAP(i) = 0.

Exemplu: Considerand reteaua din figura 1.14 avem urmatoarele reprezentari cu ajutorul tablourilor si cu ajutorul listelor simplu inlantuite:

V ρ(1) = 2, V(2) = , ρ(2) = 1 , V ρ(3) = 1, V ρ(4) = 2, V ρ(5) = 2; P = (1, 3, 4, 5, 7, 9), V = (2, 3, 4, 2, 3, 5, 3, 4); n = 5, m = 8, n + m = 5 + 8 = 13.

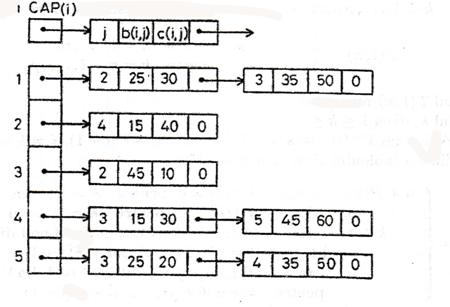
Reprezentarea prin liste de adiacenta revine la descrierea matricei de adiacenta linie cu linie. In mod similar se poate descrie matricea incidenta coloana cu coloana utilizand liste de incidenta.

Reprezentarea prin liste de incidenta consta in utilizarea tabloului uni-

dimensional P al pointerilor si a unui tablou bidimensional notat E. Daca reprezentam o retea G = ( N, A, b) sau o retea G = ( N, A, c) atunci tabloul E are trei linii si m coloane si daca reprezentam reteaua G = ( N, A, b, c) atunci tabloul E are patru linii si m coloane. Fiecare coloana k, corespunde unui arc (i, j) si anume E(1, k) = i, E(2, k) = j, E(3, k) = b(i, j) sau c(i, j) daca reteaua este G = ( N, A, b) sau G = ( N, A, c) si E(1, k) = i, E(2, k) = j, E(3, k) = b(i, j), E(4, k) = c(i, j) daca reteaua este G = ( N, A, b, c) . Tabloul E contine arcele din E(i), in ordinea stabilita, si informatiile associate acestor arce, de la coloana P(i) inclusiv pana la coloana P(i+1) - 1 inclusiv.

Exemplu: Consideram reteaua reprezentata in figura 1.14. Tablourile P si E sunt urmatoarele :

P = (1, 3, 4, 5, 7, 9)

Un alt avantaj al reprezentarii prin liste de adiacenta sau liste de incidenta este ca permite reprezentarea retelelor care contin arce paralele,

adica arce care au aceeasi extremitate initiala si aceeasi extremitate finala.

Reprezentarea prin liste de adiacenta este avantajoasa cand este implementata intr-un limbaj care are posibilitatea sa lucreze cu liste inlantuite (Pascal, C). In acest caz topologia retelei se poate modifica usor. Reprezentarea prin liste de incidenta are avantajul ca are nevoie de mai putina memorie decat reprezentarea prin liste de adiacenta. Alegerea unei reprezentari depinde de problema de rezolvat si de limbajul ales.

O retea neorientata G = ( N, A, b, c) se transforma intr-o retea orientata cu = N, = , functiile si sunt definite in raport cu problema de rezolvat si se reprezinta prin una din metodele descries mai sus.