Fractali

I.1          Prezentare generala

Un fractal defineste un obiect extrem de neregulat ale carui detalii se reproduc la fiecare scara. Denumirea sa provine din latinescul "fractus" = neregulat, frant.

Nasterea geometriei fractale i se datoreaza matematicianului suedez de origine franceza Benoit Mandelbrot (n. 1924) odata cu publicarea, in 1977, a lucrarii de referinta Geometria fractala a naturii (Fractal Geometry of Nature). In aceasta carte, Mandelbrot subliniaza ca geometria clasica, euclidiana, cu liniile ei drepte si suprafetele netede, nu poate reprezenta geometria norilor, a muntilor, samd., in masura in care o poate face geometria fractala, cu liniile ei de coasta infinit detaliate: "Norii nu sunt sfere, muntii nu sunt conuri, liniile de coasta nu sunt cercuri iar scoarta copacilor nu este neteda, nici fulgerul nu cade in linie dreapta." - Benoit Mandelbrot, "Geometria fractala a naturii", 1977.

Aceasta observatie va deschide noi orizonturi pentru matematicieni. Totodata, programatorii vor exploata tanara ramura a matematicii pentru a genera lumi artificiale extrem de realiste.

O imagine fractala este caracterizata de urmatoarea    proprietate: partitiile sale au aceeasi forma sau structura cu intregul, mai putin in urma unor modificari simple (redimensionari, reorientari samd.). Mai mult, daca fractalul este alcatuit dintr-un anumit numar de copii ale sale, fiecare redusa la o anumita scara si eventual usor modificata, el se va numi autosimilar. Importanta proprietatii de autosimilaritate este semnificativa, datorita faptului ca cea mai mare parte a obiectelor naturale sunt autosimilare. Dupa cum sublinia Mandelbrot, "muntii sunt formati din masive, care la randul lor sunt formate din masive". Doua exemple clasice de fractali autosimilari sunt: triunghiul lui Sierpinski (fractal artificial) si frunza de feriga (fractal natural).

Fig. VII .Fractali autosimilari: (a) Triunghiul lui Sierpinski, format din trei copii ale intregului la scara si (b) frunza de feriga.

Triunghiul lui Sierpinski este obtinut astfel: se considera un triunghi oarecare caruia i se traseaza liniile mijlocii (unind doua cate doua mijloacele laturilor). Se obtin astfel patru triunghiuri. Triunghiul din mijloc (format de liniile mijlocii) este eliminat si se repeta procedeul pentru cele trei triunghiuri ramase.

Fig. VII . Generarea Triunghiului lui Sierpinski

I.2          Sisteme de functii iterate (IFS) si atractori

Fie (X,d) un spatiu metric oarecare. O transformare de forma:

f(x, y) = (a*x+b*y+e, c*x+d*y+f), unde x, yIX   

si a, b, c, d, e, f constante numerice reale (parametrii transformarii), se numeste transformare afina (in R²).

O transformare afina poate fi definita in forma matriceala astfel:

.

Transformarile afine pot fi descrise ca si combinatii de redimensionari, translatii si rotatii ale spatiului, definind corespunzator parametrii a, b, c, d, e si f ai transformarii:

• a = r*cos a
• b = -s*sin b
• c = r*sin a
• d = s* cos b, unde:
• r - este factorul de omotetie pe orizontala,
• s - este factorul de omotetie pe verticala,
• a - este unghiul de rotatie fata de axa Ox,
• b - este unghiul de rotatie fata de axa Oy;
• e - reprezinta translatia pe orizontala,
• f - reprezinta translatia pe verticala.

Intr-un fractal autosimilar, fiecarei parti ii corespunde o transformare afina care descrie modificarile suferite de intreg pentru a obtine partea respectiva.

Sa consideram spre exemplu urmatorii fractali clasici:

• Triunghiul lui Sierpinski, al carui mod de obtinere a fost prezentat mai sus, poate fi descris cu ajutorul a trei transformari afine:

Tabel VII . Descrierea Triunghiului lui Sierpinski prin transformari afine

Transformarile au fost asociate astfel:

Fig. VII . Triunghiul lui Sierpinski vazut ca o reuniune a trei copii transformate ale sale

• Curba lui Koch (Linia de coasta Koch) se obtine prin procedeul: se considera un segment de dreapta care se imparte in trei parti egale, pe segmentul din mijloc se construieste un triunghi echilateral caruia i se elimina baza. Se repeta procedeul pentru cele patru segmente ramase.

Fig. VII . Generarea curbei lui Koch

Acestui fractal ii asociem patru transformari, corespunzatoare celor patru segmente numerotate astfel:

Fig. VII . Curba lui Koch vazuta ca o reuniune a patru copii transformate ale sale

Tabel VII . Descrierea Curbei lui Koch prin transformari afine

Asa cum se observa, un obiect fractal poate fi definit sub forma unui set de transformari afine contractive din X: (f_i)_i=1..n, numit Sistem de Functii Iterate (IFS). [O transformare contractiva este o transformare f a spatiului metric (X, d) astfel ca d(f(x), f(y))<s*d(x,y), oricare ar fi punctele x, yIX, unde sI(0,1) si se numeste factor de scara (sau factor de contractie)].

Daca (f_i)_i=1.n este un sistem de functii iterate (IFS), atunci trecand prin sistem o imagine oarecare, in maniera feedback, de un numar mare de ori, se va obtine intotdeauna o aceeasi imagine, numita atractorul IFS-ului [Teorema colajului].

De remarcat este faptul ca atractorul nu depinde de imaginea initiala, ci numai de transformarile efectuate, adica de catre IFS.

Acest fenomen a fost foarte bine imaginat de catre Yuval Fisher, care a "construit" un copiator aparte. Acesta este compus dintr-un set de lentile care suprapun mai multe copii ale imaginii initiale, dupa ce le-au modificat in prealabil dimensiunile. Copiatorul lui Fisher ruleaza in maniera feedback, retransmitand de fiecare data la intrare, imaginea obtinuta in urma unei prelucrari.

De exemplu, sa reducem imaginea initiala la jumatate, apoi sa o multiplicam de trei ori, dispunand cele trei copii in forma de triunghi, ca in figura de mai jos:

Fig. VII . Transformarea unei imagini

Iata rezultatul obtinut ruland copiatorul lui Fisher de trei ori, in cazul a trei imagini de intrare diferite. Se observa cu usurinta ca in ciuda varietatii formelor de intrare, imaginea rezultata este asemanatoare in cele trei situatii. Daca am fi continuat procesul de feedback, am fi obtinut cu siguranta aceeasi imagine: atractorul, care in acest caz este chiar triunghiul lui Sierpinski.

Fig. VII Copiatorul lui Yuval Fisher

Asadar, triunghiul lui Sierpinski este atractorul sistemului IFS definit astfel:

[forma matriceala]

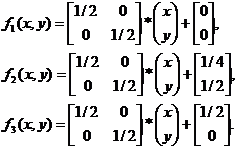
sau

[forma complexa]

f₁(z) = z/2,

f₂(z) = z/2 + + *i,

f₃(z) = z/2 + .

I.3          Problema directa si problema inversa

Posibilitatea descrierii fractalilor prin parametrii unui set finit de transformari afine duce la definirea a doua probleme duale: problema directa si problema inversa.

I.3.1         Problema directa

Problema directa consta in generarea fractalilor pe baza parametrilor ce definesc setul de transformari afine. Acest lucru nu ridica nici o dificultate. Astfel se pot obtine numerosi fractali celebri, cum ar fi: curba lui Koch, triunghiul lui Sierpinski, frunza de feriga a lui Barnsley samd.

Un algoritm extrem de simplu care rezolva problema directa este:

Implementarea acestui algoritm in limbajul C este:

Generarea fractalilor pe baza sistemului de functii iterate

void IFS(double p[][6], int n)

//n=numar transformari

//p[k][0]=omotetie pe ox

//p[k][1]=omotetie pe oy

//p[k][2]=rotatie pe ox

//p[k][3]=rotatie pe oy

//p[k][4]=translatie pe ox

//p[k][5]=translatie pe oy

I.3.2         Problema inversa

Problema inversa este cea care sta la baza compresiei fractale si a fost initiata de catre Michael Barnsley. El a reprezentat o frunza de feriga utilizand numai 24 de valori: parametrii corespunzatori a patru transformari afine. Aceasta a condus la ideea de a stoca parametrii in locul imaginii, ceea ce reduce considerabil volumul de date necesar memorarii imaginii respective. Astfel, problema inversa, mult mai dificila decat cea directa, consta in gasirea parametrilor sistemului de functii iterate care genereaza o anumita imagine (atractorul - imaginea pe care urmeaza sa o comprimam).

I.4          Dimensiunea fractala

I.4.1         Introducere

Dimensiunea unui obiect descrie modul in care ocupa acesta spatiul si deci modul in care poate fi masurat (cantitativ). Dimensiunea euclidiana, pe care o vom nota de aici incolo D, este dimensiunea spatiului euclidian in care poate fi scufundat obiectul analizat.

Dimensiunea topologica este definita pe proprietati locale ale punctelor obiectului analizat F si corespunde notiunii prin care un punct are dimensiunea 0, o linie sau o curba subtire au dimensiunea 1, suprafetele au dimensiunea 2, formele solide -volumele- sunt de dimensiune 3 samd., fara sa tina cont de dimensiunea, mai mare sau cel mult egala, a spatiului euclidian in care aceste forme sunt scufundate. Practic, dimensiunea topologica se conserva la transformarile omomorfe. Iata o definitie recursiva a dimensiunii topologice:

i.            d_T=0 daca F nu este conectata (ex. punctele izolate);

ii.          d_T=k , k>=1 daca orice pIF are o vecinatate V(p) ale carei margini au dimensiunea d_T=k-1.

Imediat se poate observa, spre exemplu, ca punctele unei curbe subtiri (k=2) au vecinatati in forma de segmente, ale caror margini sunt cate doua puncte de dimensiune d_T = k - 1 = 1. Similar, un cerc poate fi vecinatatea unui punct aflat pe o suprafata (aici, k=2), frontiera cercului fiind o curba, asa cum s-a vazut mai sus, de dimensiune d_T= k-1=1 samd.

Astfel, o suprafata unduita este scufundata intr-un spatiu euclidian de dimensiune D = 3, desi dimensiunea sa topologica este 2 (d_T = 2).   

Fig. VII . Exemple de forme geometrice de dimensiuni topologice 1 si euclidiene (primul rand), respectiv topologica si euclidiana (randul al doilea).

Observatie: In figura de mai sus, sfera nu este umpluta.

Odata cu aparitia fractalilor, caracterizarea unei forme prin dimensiunea sa topologica, exprimata printr-un numar intreg, se dovedeste a fi insuficienta. Un exemplu elocvent in acest sens este Curba lui Koch. Ea prezinta un fenomen ciudat: este o multime de puncte, de arie 0, dar de perimetru infinit: la fiecare iteratie lungimea creste de 4/3 ori. Prin urmare, utilizand geometria euclidiana, nu vom putea evalua cantitativ marimea curbei lui Koch: nu este oportun sa privim curba lui Koch ca obiect euclidian de dimensiune 1, ea avand perimetru infinit, dar nici 2-dimensional pentru ca aria sa este 0.

Fig. VII . Curba lui Koch: obiect fractal cu perimetru infinit si arie

Astfel va fi introdusa notiunea de dimensiune fractala, aceasta fiind exprimata printr-un numar rational. Dealtfel, insasi notiunea de fractal este strans legata de cea de dimensiune fractala. Un fractal este o figura a carei dimensiune fractala este strict mai mare decat dimensiunea topologica. Asa cum se observa in tabelul de mai jos, complexitatea unei figuri creste odata cu dimensiunea sa.

Tabel VII . Complexitatea unei imagini in functie de dimensiunea sa

unde reprezinta un numar infinit, iar F un numar finit.

Fractali matematici cum ar fi curba lui Koch sunt autosimilari exact, la un numar infinit de scari. Multe fenomene naturale sunt autosimilare statistic si, prin urmare pot fi mai bine descrise prin tehnici fractale decat prin metode euclidiene. Geometria fractala a fost aplicata de asemenea in cazul obiectelor naturale, cum ar fi norii, liniile de coasta, distributia punctelor de spargere a valurilor pe suprafata oceanului, imprastierea poluarii samd.

I.4.2         Dimensiunea de acoperire Hausdorff

O trasatura definitorie a obiectelor fractale este dependenta marimii lor de unitatea de masura utilizata. Acest fenomen a fost semnalat pentru prima data de catre Richardson. Dorind sa afle lungimea liniei de granita intre Spania si Portugalia, el a consultat enciclopedii ale ambelor tari. Astfel, in enciclopedia spaniola se pretindea ca granita are 987 km lungime, in timp ce enciclopedia portugheza estima la 1214 km. Explicatia ciudatului fenomen consta in utilizarea a doua unitati de masura diferite, unitatea mai mica avea sa parcurga mai multe detalii ale granitei si, prin urmare, sa obtina o masura mai mare.

Iata mai jos, reprezentata sugestiv, dependenta lungimii unei curbe de unitatea de masura utilizata.

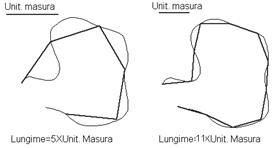
Fig. VII . Dependenta lungimii unei curbe de unitatea de masura utilizata. Cu cat pasul este mai mic, cu atat se parcurg mai multe detalii ale obiectului si, prin urmare, masura obtinuta este mai mare.

Dependenta marimii de scara utilizata face ca obiectele fractale sa fie dificil de masurat in contextul geometriei clasice. Proprietatile lor fizice (lungime, arie, volum) depind de rezolutia de reprezentare.

Folosind rationamentul lui Richardson, Mandelbrot a demonstrat ca liniile de coasta, de granita samd. sunt fractali.

In jurul anului 1914, Hausdorff defineste un nou concept asupra spatiilor topologice, sugerand astfel ca dimensiunea fractala este proportionala cu numarul minim de sfere, de raza data, necesar pentru a acoperi obiectul masurat.

Pentru a ne apropia de metodele utilizate de calculator, in cele ce urmeaza vom considera cuburi in locul sferelor.

Astfel, pentru acoperirea unei curbe de lungime 1, sunt necesare N(s)=1/s cuburi de latura s. Pentru acoperirea unei suprafete de arie 1 sunt necesare N(s)=1/s² cuburi de latura s si, in final, pentru acoperirea unui cub de volum 1 sunt necesare N(s)=1/s³ cuburi de latura s (fig. VII.11.). In general, se verifica relatia:

N(s) ~1/s^D

unde:

N(s) este numarul de cuburi necesare;

s este latura unui cub;

D este dimensiunea obiectului.

Fig. VII . Acoperirea a trei figuri euclidiene cu cuburi de laturi egale

Logaritmand relatia de mai sus, putem deduce D:

D~log(N(s))/log(1/s) (1)

Asadar, dimensiunea Hausdorff, cunoscuta si ca dimensiunea Hausdorff-Besicovich, este definita prin cea mai eficienta acoperire, dupa cum urmeaza:

Fie d,s IR si fie un set de functii de test, astfel incat N(s) este numarul de sfere de diametru s (cuburi de latura s) necesare pentru a acoperi multimea data F. Atunci, exista o valoare reala unica d=D_H, numita dimensiune Hausdorff a lui F, astfel ca:

Masura ce caracterizeaza un obiect cu dimensiunea Hausdorff este data de relatia:

Iata, spre exemplu, reprezentarea grafica a dependentei masurii curbei lui Koch fata de dimensiunea obiectului, unde N_n este numarul de sfere de acoperire de diametru s_n, iar d este dimensiunea presupusa a obiectului, care ia, demonstrativ, diferite valori. Se observa ca valoarea optima pentru d este cuprinsa intre 1.2 si 1.3, intrucat pentru valori sub 1.2 masura obtinuta tinde catre infinit, iar pentru valori superioare lui 1.3 masura tinde catre 0.

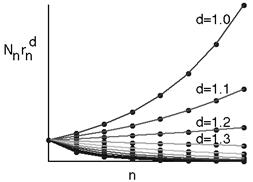
Fig. VII . Dependenta masurii curbei lui Koch de dimensiunea sa

Dimensiunea Hausdorff este cea mai acceptata definitie a dimensiunii fractale, insa este dificil de calculat. In practica, dimensiunea fractala este estimata cu ajutorul dimensiunii autosimilare sau a dimensiunii box-counting.

Initial, Mandelbrot a definit fractalii, asa cum au fost si denumiti (fractus), ca acele forme cu detalii infinite, la orice nivel. Apoi, a revenit asupra definitiei, enuntand conceptul de autosimilaritate, afirmand ca fractalii sunt acele forme alcatuite din parti similare, intr-un anumit fel, cu intregul. In cele din urma a dat o noua definitie, singura formala dealtfel, prin care fractalii sunt formele a caror dimensiune Hausdorff depaseste strict dimensiunea topologica:

D_H>D_t

I.4.3         Dimensiunea fractala autosimilara

O trasatura fundamentala a fractalilor este similaritatea. Mandelbrot observa ca o linie de coasta, privita din avion, arata ca o dreapta, dar pe masura ce ne apropiem, ea devine din ce in ce mai fragmentata, mai delicata, la orice nivel de detaliere ea semanand cu intregul. Plecand de la aceasta observatie, Mandelbrot a dat o prima definitie a fractalilor ca fiind acele obiecte alcatuite din copii ale lor, la alta scara.

Exista mai multe tipuri de similaritate:

autosimilaritatea (similaritate perfecta)- obiectul este alcatuit din copii ale sale, la diferite scari de reprezentare. In general, acest tip de similaritate este intalnit la fractalii artificiali, generati pe calculator si prezinta avantaje majore in aplicatii cum ar fi compresia fractala.

Asa cum am aratat mai sus, triunghiul lui Sierpinski este alcatuit din trei copii ale sale la scara .

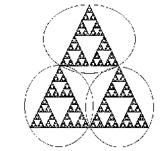
Fig. VII . Fractal autosimilar: Triunghiul lui Sierpinski, format din copii ale intregului la scara

similaritatea pe portiuni - obiectul este alcatuit din copii similare intre ele. Acest tip de similaritate este intalnit atat la fractalii artificiali cat si la cei naturali. Similaritatea pe portiuni a fost observata de Jaquin, care a construit, pe baza ei, un puternic algoritm de compresie de imagini bazat pe tehnici fractale, ale carui rezultate au fost incurajatoare atat pentru imagini artificiale, cat mai ales pentru cele reale.

browniana - obiectul este fragmentat in parti aleatoare, ce prezinta detalii la fiecare nivel. Similaritate browniana intalnim la plasma-fractali, utilizati in crearea liniilor de coasta reale sau a peisajelor.

O categorie importanta de forme fractale studiate de catre geometria fractala, este reprezentata de fractalii artificiali (generati pe calculator), dintre care o mare parte prezinta proprietatea de autosimilaritate (triunghiul lui Sierpinski, linia de coasta Koch, praful lui Cantor, dragonul lui Heighway si multi altii). Plecand de la ideea ca dimensiunea fractala are ca scop evaluarea gradului de fragmentare a unui obiect, pentru categoria obiectelor fractale autosimilare exista o interpretare simpla a formulei (1):

D_f=log(Numar copii autosimilare) / log(factor de contractie)

Spre exemplu, in cazul triunghiului lui Sierpinski, avem trei copii ale imaginii, cu magnificatia 2, deci dimensiunea fractala va fi:

D_f=log(3) / log(2) = 1.5849

Asadar, dimensiunea autosimilara masoara invarianta (de scara) a obiectului F la transformari afine (redimensionari, translatii, rotatii). Aceasta metoda de calcul presupune ca obiectul analizat este autosimilar. Totusi, exista o generalizare, numita auto-afinitate, ce denota o invarianta statistica de scara.

I.4.4         Algoritmul box-counting

Algoritmul box-counting este utilizat pentru determinarea automatizata a dimensiunii fractale in cazul imaginilor digitale binare monocrome, stocate ca matrici de pixeli (bitmap).

I.4.4.1   Dimensiunea box-counting

Asa cum am aratat mai sus, prin acoperirea obiectului fractal cu cuburi de latura data s, se ajunge ca:

D~log(N(s))/log(1/s) (1)

Este de asteptat ca, pentru s cat mai mic, aproximatia de mai sus sa fie cat mai buna:

D = lim_{s -> 0}log(N(s))/log(1/s)

Daca aceasta limita exista, ea este denumita dimensiunea box-counting a obiectului masurat. Pentru ca, in practica, aceasta limita converge lent, se utilizeaza o cale alternativa. Intrucat,

log(N(s)) = D*log(1/s)

este ecuatia de variabila s a unei drepte de panta D, se traseaza curba log-log, descrisa prin punctele de coordonate (log(N(s), log(1/s)), si, prin regresie liniara (metoda celor mai mici patrate), se determina panta curbei, aceasta fiind dimensiunea fractala cautata:

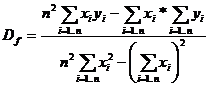
unde x_i=log(1/s), iar y_i=log(N(s)), pentru diferite valori ale factorului de scara s.

I.4.4.2   Descrierea algoritmului

Algoritmul box-counting presupune determinarea dimensiunii fractale in functie de evolutia marimii obiectului in raport cu factorul de scara utilizat. El consta in impartirea succesiva a imaginii in 4, 16, 64 samd. patrate egale si numararea, de fiecare data, a patratelor care acopera obiectul. Punctele de coordonate (log(N(s), log(1/s)) -unde s este latura comuna a patratelor de acoperire, iar N(s) este numarul de patrate ce contin informatie- vor fi asezate aproximativ pe o dreapta a carei panta este dimensiunea box-counting.

Sa consideram urmatoarea imagine:

Fig. VII . Imagine monocroma

Vom aplica apoi algoritmul box-counting, descris mai sus (nu au fost trasate decat patratele care contin informatie).

Fig. VII . Aplicarea algoritmului box-counting

Se obtin valorile:

Tabel VII . Variatia N(s) fata de factorul de scara     s

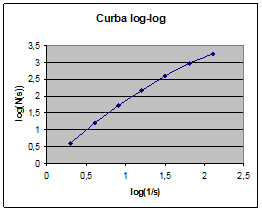
Fig. VII . Curba log-log formata din punctele de coordonate (log(N(s), log(1/s))

Utilizand metoda celor mai mici patrate, cu formula de mai sus, deducem ca punctele (log(N(s), log(1/s)), descriu, cu aproximatie, o dreapta cu panta 1.39.

Se cunosc P[nW][nH] matrice binara reprezentand imaginea:

si nMaxIter, numarul de impartiri succesive ale imaginii.

O implementare recursiva a algoritmului box-counting in limbajul C este:

Algoritmul box-counting

class CRect

int *N=new int[nMaxIter];//vectorul N(s)

BoxCounting(int nIter,CRect dr)

Apelul functiei va fi BoxCounting(0,CRect(0,0,nW,nH)).