Metode euristice de programare

Metode euristice

I.1.1         Descrierea metodei

O mare parte a algoritmilor de optim au un timp de executie de ordin exponential si necesita o cantitate mare de memorie. Pentru eliminarea acestui inconvenient, adeseori in practica sunt elaborati algoritmi care furnizeaza solutii nu neaparat optime, dar "suficient de bune" intr-un timp mult mai scurt si necesitand o cantitate de memorie acceptabila. Elaborarea acestor algoritmi are la baza, de regula, idei naturale, empirice, "de bun simt".

In cea mai mare parte a cazurilor, algoritmii Greedy incep ca algoritmi euristici, in care alegerea unui element se face astfel incat sa produca un optim local. Ulterior, in cazul algoritmilor Greedy, se demonstreaza faptul ca optimul local implica optim global.

Asadar, un algoritm euristic are urmatoarele doua proprietati:

furnizeaza solutii "suficient" de bune, nu neaparat optimale;

este usor de implementat si obtine rezultate intr-un timp rezonabil, mai scurt decat in cazul utilizarii altor algoritmi optimali.

O abordare uzuala este aceea de a descompune procesul de cautare a solutiei in mai multe etape succesive, din fiecare etapa rezultand solutii optime (locale) pentru acea etapa. Evident ca o asemenea abordare nu va conduce in mod obligatoriu la un optim global. In categoria algoritmilor euristici se incadreaza algoritmii elaborati cu metoda Greedy, care nu genereaza solutia optima, sau pentru care nu s-a demonstrat acest lucru.

Algoritmii euristici sunt preferati in situatii cum ar fi:

atunci cand urmeaza a fi utilizati de un numar mic de ori, ceea ce face ca un efort mare de programare sa nu se justifice;

cand efortul de determinare a unei solutii optime este prea mare fata de castigul obtinut.

Totusi algoritmii euristici trebuie priviti ca o solutie de start ce furnizeaza o idee de rezolvare; ei nu trebuie folositi in exces daca nu au fost testati, analizati si verificati, deoarece pot duce la solutii ineficiente care in practica pot fi dezastruoase.

I.1.2         Exemplu - Programarea aplicatiilor pe procesoare

Sa consideram problema programarii unor aplicatii pe mai multe procesoare: Se cere programarea a m aplicatii independente de durate (lungimi) diferite L= pe n procesoare astfel ca timpul de executie a lor (in ansamblu) sa fie cat mai mic, stiind ca:

procesoarele pot functiona simultan si pot procesa orice aplicatie;

procesarea unei aplicatii, odata inceputa pe un procesor, nu poate fi intrerupta si, deci, nici mutata pe alt procesor.

O programare este bine definita daca:

o aplicatie neprogramata este preluata de primul procesor liber;

procesoarele intra in functiune fara intarzieri.

Este evident ca problema programarii se pune atunci cand numarul de procesoare este mai mic decat numarul de aplicatii.

De exemplu, sa presupunem ca avem de programat pe n=3 procesoare m=5 aplicatii cu timpii de executie L=, atunci o programare ar putea fi:

Procesor 1 : | 6

Procesor 2 : | 6

Procesor 3 : | 3 2 | 9 |

si ar necesita timpul maxim T=14, pe care am putea incerca sa il reducem, avand in vedere ca primele doua procesoare au o perioada suficient de mare de pauza.

Dupa mai multe incercari putem ajunge la programarea:

Procesor 1 : 9 |

Procesor 2 : | 6 3 |

Procesor 3 : | 6 2 |

care necesita T=9 si care, dealtfel, este programarea optima, avand in vedere faptul ca exista o aplicatie cu timpul de executie 9.

Procedeul euristic utilizat provine dintr-o idee "de bun simt" si anume aceea de a alege, de fiecare data, aplicatia neprogramata cu cel mai mare timp de executie si a o programa pe procesorul care se va elibera primul. In acest sens, se va efectua in prealabil o sortare a aplicatiilor in ordine descrescatoare a timpilor lor de executie.

Algoritmul este descris astfel:

Algoritmul este euristic deoarece alegerea aplicatiei neprogramate cu timp maxim de executie nu duce in mod obligatoriu la o programare optimala. Iata spre exemplu, in situatia in care dispunem de numai 2 procesoare, iar timpii de executie sunt L=, programarea obtinuta prin metoda de mai sus va fi:

Procesor 1 : | 3 2 | 2 |

Procesor 2 : | 3 2 |

si va necesita T=7, mai mult decat in cazul:

Procesor 1 : | 3

Procesor 2 : 2 | 2 | 2 | cu T=6.

Se poate verifica usor ca solutiei de rezolvare de mai sus i se poate asocia un timp de calcul astfel:

de ordin O(m*log₂m), pentru pasul 1, datorat utilizarii unui algoritm performant de sortare

doua parcurgeri imbricate de vectori, cel al aplicatiilor (de dimensiune m) si respectiv cel asociat timpilor de ocupare a procesoarelor (de dimensiune n) de la pasul 2, de complexitate O(m*n).

Cum n<=m, rezulta ca avem un algoritm polinomial de complexitate O(m²).

Solutia problemei va fi reprezentata sub forma unui vector P cu m elemente, unde fiecare P[i]=procesorul pe care va fi executata lucrarea i.

Daca se doreste obtinerea solutiei optime, problema va fi abordata cu alte metode, insa cu rezervele impuse de timpul de calcul exponential si memoria mare necesara. De exemplu, poate fi utilizata metoda Backtracking, avand in vedere modul in care a fost definita solutia P=^m, spatiu finit. Pentru a grabi gasirea programarii optime, metoda Backtracking poate fi combinata cu Greedy, in sensul ca se retine ultima programare optima obtinuta si daca, pe parcursul generarii unei pre-solutii, aceasta necesita un timp total mai mare decat al solutiei optime curente, atunci se renunta la aceasta pre-solutie.

I.1.3         Aplicatii

I.1.3.1   Programarea aplicatiilor pe n procesoare, euristic

Enuntul problemei a fost precizat mai sus.

Solutie:

Programarea aplicatiilor pe procesoare-varianta euristica

#include<iostream.h>

void ProgLucr(int *L,int *P,int m,int n)

delete[]T;

main()

ProgLucr(L,P,m,n);

for(i=0;i<m;i++)

cout<<' Aplicatia de durata '<<L[i]<<

' alocata pe procesorul '<<P[i]<<endl;

delete[]P;

delete[]L;

return 0;

I.1.3.2   Programarea optimala a aplicatiilor pe n procesoare

Asa cum am aratat mai sus, putem utiliza Backtracking combinat cu Greedy pentru a obtine solutia optima, fara a explora spatiul solutiilor in intregime. Se utilizeaza in plus vectorul POpt in care se retine solutia optima curenta si valoarea TOpt, timpul total corespunzator acesteia.

Solutie:

Programarea optimala a aplicatiilor pe procesoare

#include<iostream.h>

int n,m,*L,*P,*POpt;

int TOpt=1e6;//intreg mare

int timp(int k)

int cont(int k)

void retsol()

void ProgLucr(int k)

}

main()

ProgLucr(0);

for(i=0;i<m;i++)

cout<<'Aplicatia de durata '<<L[i]<<

' alocata pe procesorul '<<POpt[i]<<endl;

cout<<'Timp ocupare: '<<TOpt;

delete[]POpt;

delete[]P;

delete[]L;

return 0;

Creat cu metoda Backtracking, algoritmului programarii aplicatiilor pe procesoare ii poate fi asociat un timp exponential de ordin O(n^m).

I.1.3.3   Colorarea hartilor cu 4 culori

Problema colorarii hartilor a fost deja rezolvata cu metoda Backtracking. Se cerea colorarea unei harti, data prin matricea de vecinatati ale tarilor, cu un numar dat de culori (se poate demonstra ca patru culori sunt suficiente). Cu metoda Backtracking s-a creat un algoritm exponential care, in situatia in care dorim sa coloram harta lumii spre exemplu, necesita un timp de executie indelungat. De aceea, se impune crearea unui alt algoritm, de ordin polinomial, care sa furnizeze o solutie intr-un timp rezonabil, chiar daca aceasta solutie nu admisibila sau nu foloseste un numar minim de culori.

Ideea euristica ce sta la baza acestui algoritm este de a colora pe rand fiecare tara cu prima culoare pe care vecinii deja colorati sai nu o folosesc.

Solutie:

Colorarea hartilor cu 4 culori - metoda euristica

#include<iostream.h>

#include<math.h>

int *X,**V,n,r=4;

char *culori[]=;

void harta()

main()

harta();

for(i=0;i<n;i++)

cout<<endl<<'Tara '<<i<<'-> culoarea '<<culori[X[i]];

for(i=0;i<n;i++)

delete V[i];

delete V;

delete[]X;

return 0;

Algoritmul propus, creat printr-o metoda euristica, are complexitate polinomiala O(n³).

I.1.3.4   Traseul comis-voiajorului

Se considera n orase legate doua cate doua prin drumuri. Fiecare drum are asociat un cost cunoscut necesar parcurgerii sale. Un comis-voiajor trebuie sa plece dintr-un oras, sa treaca o singura data prin toate celelalte si sa se intoarca de unde a plecat astfel incat sa parcurga un drum de cost cat mai mic. Se cere sa se determine traseul comis-voiajorului.

Cu alte cuvinte, putem privi orasele ca noduri ale unui graf ponderat complet, ponderile fiind costurile dintre orase. Problema cere sa se determine un circuit hamiltonian.

Exemplu:

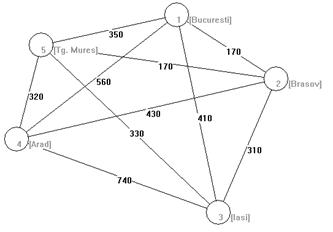
Fig. V . Orasele si drumurile dintre ele

In acest exemplu am considerat drept costuri chiar distantele intre orase.

Indicatie:

O idee naturala, specifica metodelor euristice, este aceea de a pleca din orasul initial catre cel mai apropiat oras (cu cel mai mic cost al deplasarii) si tot asa, avand grija sa nu trecem de doua ori prin acelasi oras. Cand toate orasele au fost vizitate, ne intoarcem in orasul initial.

Reprezentam solutia problemei sub forma unui vector Traseu[0..n] cu n+1 elemente, unde Traseu_k reprezinta al k-lea oras vizitat. Fara a restrange generalitatea, presupunem ca se pleaca din primul oras (orasul 0), lantul generat oricum vizitand toate orasele.

In exemplul de mai sus, fie Bucuresti orasul de plecare. Algoritmul va furniza solutia:

Bucuresti Brasov Tg. Mures Arad Iasi Bucuresti, in total 1810 km.

Insa algoritmul euristic prezentat nu furnizeaza intotdeauna solutia optima. Chiar in exemplul de mai sus, cunoscand harta Romaniei, o alegere mai naturala ar fi:

Bucuresti Brasov Iasi Tg. Mures Arad Bucuresti,

care conduce intr-adevar la un total mai mic, de numai 1690 km. Solutia optima a problemei poate fi obtinuta combinand Backtracking cu Greedy, insa unui astfel de algoritm ii va fi asociat un timp de calcul exponential: solutia Traseuⁿ este spatiu finit, deci se poate aplica Backtracking. Il putem combina cu Greedy pentru a reduce cautarea in spatiul solutiilor: daca pre-solutia curenta are un cost mai mare decat solutia curenta optima, atunci oprim generarea ei.

Revenind la implementarea algoritmului euristic, mai folosim un vector suplimentar Vizitat cu n elemente, unde:

Fie Cost, matricea de adiacente asociata grafului si cost costul curent al traseului la un moment dat.

Traseul comis-voiajorului

#include <iostream.h>

int ComisVoiajor(int *Cost[], int n, int *Traseu)

//incudem nod_nou in traseu si ne deplasam in el

Traseu[i]=nod_nou;

cost+=cost_min;

Vizitat[nod_nou]=1;

nod_curent=nod_nou;

}

//incheiem lantul: inludem in traseu nodul initial

Traseu[n]=0;

cost+=Cost[nod_curent][0];

delete[]Vizitat;

return cost;

main()

cout<<'Costurile dintre orase:'<<endl;

for(i=0;i<n;i++)

for(int j=i+1;j<n;j++)

cout<<'Traseul are costul '<<ComisVoiajor(Cost,n,Traseu)<<

' si consta in:'<<endl;

for(i=0;i<=n;i++)

cout<<Oras[Traseu[i]]<<' ';

for(i=0;i<n;i++)

delete[]Oras[i];

delete[]Oras;

delete[]Traseu;

for(i=0;i<n;i++)

delete[]Cost[i];

delete[]Cost;

return 0;

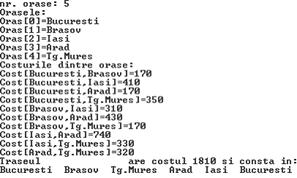
Pentru datele de intrare propuse, vom avea: