Algoritmi Recursivi

Algoritmi Recursivi

Definitie. Clasificari.

Recursivitatea este o proprietate a obiectelor care sunt partial definite in termeni ai lor insisi. Cel mai concludent exemplu al acestei proprietati il constituie sirurile numerice din matematica definite recursiv:

f₀=1, f₁=1,, f_n=f_n-1+ f_n-2, n>=2

Recursivitatea nu tine insa doar de domeniul matematicii, ea este proprie unei categorii mult mai largi de obiecte, printre care si acela al algoritmilor. Vom discuta de implementarea acestora intr-un limbaj de programare sub forma de functii, sau proceduri recursive.

Proprietatea principala a functiilor si procedurilor recursive consta in referirea in cadrul acestora la functia, sau procedura insasi.

Procedurile sau functiile recursive sunt folosite in special pentru acele categorii de algoritmi care lucreaza cu structuri de date definite recursiv. Se vor prezenta doua exemple tipice:

a) structurile algebrice definite pe numerele naturale:

-functia factorial n!:

-0!=1,

-daca n>0, atunci n!=n*(n-1)!.

b) structurile arborescente:

-'O' este un arbore (arbore vid),

-daca t1 si t2 sint arbori, atunci t1*t2 este un arbore.

Pentru calculul functiei factorial de mai sus, se poate scrie urmatoarea functie:

int fact(int n)

Pentru a apela aceasta functie cu valoarea n=5, se obtin apeluri repetate la functia insasi, scazind cu 1 valoarea argumentului, pina cind n=0 si in acest caz fact=1;

fact(5)=5*fact(4)=5*(4*fact(3))=5*(4*(3*fact(2)))=

=5*(4*(3*(2*fact(1))))=5*(4*(3*(2*(1*fact(0)))))=

=5*(4*(3*(2*(1*1))))=5*(4*(3*(2*1)))=5*(4*(3*2))=5*(4*6)=5*24 =120

Se observa ca valorile argumentului 5,4,..1 la care s-au facut referiri trebuie memorate pina se gaseste n=0, pentru a putea servi drept factori in procesul de inmultire.

O asemenea conditie pe care trebuie sa o indeplineasca un algoritm succesiv recursiv se numeste conditie de oprire, sau conditie de consistenta: - valorile pe care le calculeaza un algoritm recursiv trebuie sa fie ori direct calculabile, ori calculabile cu ajutorul unor valori direct calculabile.

Se observa definitia descendenta a unui asemenea algoritm spre deosebire de o definitie ascendenta care plecind de la valorile initiale fact(0)=1, calculeaza orice termen superior fact(n)=n*fact(n-1).

Tot din exemplul anterior se observa modul specific in care se poate implementa un algoritm recursiv de catre un compilator ce admite asemenea definitii: - folosirea unei stive in care sunt memorate toate argumentele la care s-au facut referiri in procesul aplicarii definitiei. In cazul concret n=5, in stiva se memoreaza pe rind valorile 5,4,3,2,1, iar cind 'fact' se poate calcula direct pentru n=0 se inmulteste valoarea acestuia cu valorile scoase pe rind din stiva, memorindu-se rezultatul.

Daca o procedura (functie) contine in cadrul ei o referire explicita catre ea insasi, procedura (functia) se numeste direct recursiva. Daca o procedura (functie) contine o referire catre o alta procedura (functie) care contine la rindul ei (direct, sau indirect) referire catre procedura initiala, atunci ea se numeste indirect recursiva.

Deci, o functie se spune ca este recursiva daca se apeleaza pe ea insasi, fie direct, fie indirect.

Exemplu:

#include <stdio.h>

void recursiv ()

void main ()

Acest program ar trebui sa tipareasca numerele 1,2,3, pina la infinit, practic pina se umple stiva de memorie si programul va fi intrerupt de o rutina de eroare. Deci trebuie sa se introduca un criteriu de stop.

/* exemplul anterior modificat */

void recursiv1 ()

}

#include <stdio.h>

void main()

Observatie:

Se noteaza faptul ca programul nu s-ar sfirsi daca variabila 'count' era 'automatic', decit daca este fixata, deoarece ar fi creata in mod dinamic o noua variabila numita 'count' si reinitializata la 1 cu fiecare apel. Acesta este un important aspect al recursivitatii - pentru fiecare apel, compilatorul creaza un intreg nou set de variabile de tip 'automatic'. Chiar daca aceste variabile au acelasi nume, ele refera diferite zone de memorie.

Folosirea variabilelor fixate este un mod de control al recursivitatii. O alta metoda este folosirea valorilor de intrare.

Urmatoarea functie foloseste recursivitatea pentru a calcula suma intregilor intre '1' si 'n'.

int sum(n)

int n;

Este folositor sa se faca fiecare pas prin functie, observind ce valori se returneaza cu fiecare apel. Daca se transmite functiei valoarea 5, urma apelurilor este data in figura urmatoare.

Notam ca nu se intoarce nici un apel pina cind toate subapelurile lor s-au returnat. In exemplu, aceasta nu se intimpla pina cind 'n' nu este mai mic sau egal cu ,1 in timp ce functia se 'desfasoara' ea insasi.

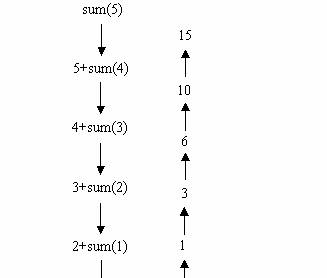
Mai intii se returneaza 1, care este adunat la 2 si se returneaza valoarea 3 care este adunata la 3 si se returneaza 6 care este adunata la 4 si se returneaza 10 care este adunat la 5 si se returneaza 15.

Programele recursive sint greu de conceptualizat la inceput, dar ele sint foarte puternice.

Totusi trebuie amintit faptul ca recursivitatea nu este in mod necesar mai eficienta decit iteratia deoarece calculatorul trebuie sa aloce spatiu in stiva aditionala pentru fiecare apel si o recursivitate destul de adinca poate conduce la depasirea spatiului alocat pentru aceasta activitate de catre sistemul de operare.

Exemple

Un prim exemplu il constitue transcrierea intr-o procedura recursiva (functie recursiva) a unei functii din algebra, definita recursiv.

Se stie urmatoarea relatie referitoare la combinari: si daca m>n precum si

Putem defini o functie recursiva pentru calculul acestor combinari astfel:

int comb(int m, int n)

Un alt exemplu, tot din matematica, il constituie functiile care desi nu au definitie recursiva, prin operatiile care le implica, se pot defini astfel: - in cazul calculului restului impartirii a doua numere intregi, se scade al doilea numar din rezultat pina cind primul numar devine mai mic decit al doilea numar, care este chiar rezultatul impartirii;

int rest(int a, intb)

O alta categorie de probleme ce se pot rezolva folosind proceduri recursive o constituie prelucrarile de texte. In acest caz nu mai exista definitii recursive aprioric, scrierea recursiva a algoritmilor respectivi trebuie analizata in fiecare caz in parte.

De exemplu, o problema relativ simpla este tiparirea unui numar intreg ca un sir de caractere. Exista cel putin doua solutii la rezolvarea acestei probleme: - una nerecursiva, folosind un vector pentru memorarea cifrelor numarului cu tiparirea ulterioara a acestora si una recursiva care incepind de la sfirsit, tipareste fiecare cifra si retine numarul obtinut prin eliminarea acesteia.

Pentru varianta nerecursiva putem scrie urmatoarea functie:

void printd(int n)

i=0;

do

while (n>0);

for (j=i; j>=1; j--) printf('%c', v[j-1]);

}

Pentru varianta recursiva, se poate scrie:

void printd(int n)

i=n/10;

if (i!=0) printd(i);

printf('%c',(char)(n/10+(int)'0'));

}

Pentru a tipari numarul 457 in varianta recursiva se apeleaza din nou procedura pentru numarul 45 si se tipareste 7 cind se face revenire; pentru 45 se apeleaza din nou procedura pentru 4 si se tipareste 5 cind se revine, iar pentru numarul 4 nu se mai face nici un apel de procedura, in schimb se tipareste numarul 4.

Un alt exemplu este acela care transforma o expresie algebrica in notatie postfixa (notatie poloneza inversa). Pentru aceasta consideram urmatoarele reguli sintactice:

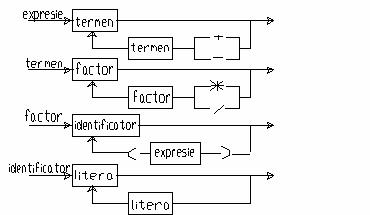
De exemplu expresia (ab+ba)*(c-d) trebuie transformata in:

ab*ba*+cd-*

Deoarece, definitiile sintactice sunt date recursiv, procedurile pentru determinarea acestora implica o scriere recursiva.

Programul contine cite o procedura pentru fiecare definitie sintactica si o procedura pentru citirea caracterelor expresiei. Se considera ca textul ce contine expresiile se termina cu caracterul '.'.

#include <stdio.h>

#include <stdlib.h>

void expr(void);

void fact(void);

char ch;

char lot[255];

int nrlot=-1;

FILE* f;

void inset(char ch, char *lot)

/* Verifica daca caracterul ch se afla in multimea lot */

int ch_in_lot(char ch, char *lot)

void urm(void)

/* Citeste urmatorul caracter din fisierul 'f' */

void ident(void)

/* Tipareste caracterele din fisier care sunt in

multimea 'lot'    */

printf(' ');

void fact(void)

/* Daca s-a intilnit o paranteza deschisa, se analizeaza expresia dintre ea si paranteza inchisa corespunzatoare */

else ident();

void term(void)

/* Analizeaza operatorii '*' si '/' */

void expr()

/* Evalueaza o espresie dintre doua paranteze */

if ((ch == ')') || (ch == 'r')) urm();

void main()

while (!(feof(f)));

fclose(f);

Urmatorul exemplu este luat din programele care lucreaza cu structurile arborescente, arbori binari (vezi si capitolul doi). Un arbore binar este o structura de date definita recursiv:

typedef struct arb

nod;

Cimpul 'key' reprezinta un cimp de informatie utila atasata unui element al arborelui (cheia de identificare), iar cimpurile 'left' si 'right' reprezinta pointeri catre nodurile descendente din stinga, respectiv dreapta elementului curent.

Programele care lucreaza cu asemenea structuri de date se pot construi in mod recursiv.

Programul urmator construieste un arbore binar si apoi il parcurge in trei moduri:

-in preordine (se viziteaza radacina, apoi se parcurge subarborele sting si apoi cel drept);

-in postordine (se parcurge subarborle sting, apoi cel drept, apoi se viziteaza radacina);

-in inordine (se parcurge subarborele sting, se viziteaza radacina si apoi se parcurge subarborele drept).

Informatia aferenta nodurilor se citeste dintr-un fisier text considerind elementele in preordine, iar caracterul '.' indicind un subarbore vid.

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

#include <ctype.h>

typedef struct arb parb;

parb *rad=NULL;

int cheie,val;

char ch;

parb *adauga(int val,parb *rad)

/* Adauga un element in arbore, recursiv, in inordine*/

else

return (aux);

void preordine(parb *rad)

/*Parcurge arborele in preordine*/

void inordine(parb *rad)

/*Parcurge arborele in inordine*/

void postordine(parb *rad)

/*Parcurge arborele in postordine*/

void main()

printf('Arborele parcurs in preordine:n');

preordine(rad);

printf('Arborele parcurs in inordine:n');

inordine(rad);

printf('Arborele parcurs in postordine:n');

postordine(rad);

In sfarsit un ultim exemplu este luat din teoria jocurilor.

Problema urmatoare poarta numele de 'Problema turnurilor din Hanoi'. Se considera 3 tije numarotate a, b, c si 'n' discuri perforate de diametre diferite. Initial discurile sunt puse pe 'a' in ordine crescatoare a diametrelor (incepind de la virf).

Problema care se pune este aceea de a muta toate discurile pe tija 'b' folosind si tija 'c' respectind urmatoarele reguli:

-la fiecare pas se muta un singur disc

-tot timpul, pe fiecare tija, deasupra unui disc pot apare numai discuri cu diametre mai mici.

O mutare o putem scrie ca o pereche (i,j), cu semnificatia ca se muta un disc de pe tija 'i' pe tija 'j'.(i,j )

Daca notam cu H(m,i,j) sirul mutarilor necesare pentru a muta primele 'm' discuri (cele mai de sus) de pe tija 'i' pe tija 'j' folosind si tija k=a,b,c cu (i,j) respectind regulile de mai sus, problema consta in a determina sirul de mutari H(n,a,b).

Se observa ca se poate scrie:

H(n,i,j)= - (i,j) pentru n=1

H(n-1,i,k), (i,j), H(n-1,k,j) pentru n>1

Astfel se reduce problema celor "n" discuri la doua probleme pentru (n-1) discuri. Plecind de la H(n,a,b), se obtin succesiv secventele:

H(n-1,a,c),(a,b),H(n-1,c,b)

H(n-2,a,b),(a,c),H(n-2,b,c),(a,b),H(n-2,c,a),(c,b),H(n-2,a,b) etc.

Rezulta ca se poate scrie o procedura recursiva, considerind tijele a, b, c ca formind o multime de numere intregi:1, 2, 3

#include <stdio.h>

#include <stdlib.h>

#include <string.h>

#include <ctype.h>

typedef int rang;

int n;

void han(int n,rang i,rang j)

}

void main()

Eliminarea procedurilor recursive

Algoritmii recursivi se pot inlocui cu proceduri care folosesc stive, sau proceduri iterative.

Cele mai multe functii recursive pot fi scrise intr-o forma iterativa echivalenta. Dar codul pentru sarcina de executat este mai usor de scris si intretinut atunci cind se foloseste recursivitatea.

Totusi, nu intotdeauna un algoritm recursiv este calea cea mai simpla de rezolvare a unei probleme. La fiecare nou apel recursiv al procedurii se face o copie a acesteia cu toti parametrii, astfel incit daca este necesar a se efectua calcule relativ simple, este preferabil a se folosi o varianta iterativa a respectvei proceduri.

Spre exemplu, in locul procedurii recursive pentru calculul functiei factorial se poate scrie iterativ astfel:

int fact1(int n)

return f;

}

Se poate de asemenea scrie o varianta iterativa in care calculele se petrec in mod ascendent:

int fact2(int n)

}

In general algoritmii numerici recursivi pot fi trecuti cu usurinta in varianta iterativa, desi ei nu constituie singura clasa de algoritmi. Exista insa si categorii de algoritmi care au o structura esential recursiva si este indicat sa se pastreze aceasta structura.

In cazul in care se lucreaza pe masini nerecursive, cum este cazul compilatorului Fortran trebuie transcrisi algoritmii in varianta iterativa sau se poate simula folosirea stivei pentru a le pastra caracterul recursiv.

In continuare se descrie un algoritm cu ajutorul caruia se poate elimina recursivitatea directa folosind o stiva.

La inceputul procedurii (sau functiei) trebuie declarat zona de memorie pentru folosirea stivei. Stiva trebuie dimensionata astfel incit sa poata retine valorile parametrilor, variabilelor reale, valoarea functiei (daca este functie) si adresa de revenire la fiecare apel recursiv. Stiva si pointerul spre inceputul ei se trateaza ca fiind variabile globale.

1) Se initializeaza stiva ca fiind vida la inceputul procedurii (functiei)

2) Se ataseaza eticheta L0 primei instructiuni executabile.

3) Fiecare apel recursiv la procedura (functie) se inlocuieste cu un set de instructiuni dupa cum urmeaza:

a) se memoreaza valoarea parametrilor care nu sunt de iesire si a variabilelor locale in stiva.

b) se creeaza o eticheta Li si se memoreaza 'i' in stiva (valoarea 'i' este folosita pentru a determina adresa de revenire din procedura)

c) se evalueaza argumentele apelului si se asociaza aceste valori parametrilor formali corespunzatori.

d) se insereaza un salt neconditionat spre inceputul procedurii (eticheta L0)

e) daca este o procedura, eticheta Li creata la pasul 3.b. se asociaza instructiunii executabile imediat urmatoare saltului neconditionat. Daca este o functie, se ataseaza eticheta L1 (tot dupa saltul neconditionat) la o noua instructiune ce extrage din virful stivei valoarea functiei (actulizind si pointerul stivei) asociind-o variabilei respective din instructiunea unde apare apelul.

4) La iesirea din procedura (sau functie) se inseraza instructiuni, conform regulilor:

a) daca stiva este vida se executa 'return' normal

b) altfel se extrage din stiva adresa 'i' de revenire si se asociaza aceasta unei variabile speciale.

c) se extrag din stiva valorile variabilelor locale si parametrilor care nu sunt de iesire.

d) daca este o functie se memoreaza in stiva valoarea calculata a functiei (modificind si pointerii stivei)

e) se face salt la adresa de revenire Li utilizind valoarea 'i' extrasa la pasul b.

Se remarca faptul ca daca intr-o procedura (functie) recursiva exista un singur apel recursiv, etichetele Li se reduc la una singura L1 si valoarea '1' nu mai are nevoie sa se memoreze in stiva la pasul 3.b., iar saltul de la pasul 4.f. se face intotdeauna la eticheta L1 (deci nu se mai extrage valoarea 'i' la pasul 4.c.)

Parametrii de iesire (declarati cu 'var') nu este nevoie sa fie memorati in stiva, chiar daca s-ar memora la un apel recursiv (la pasul 3.a.), la revenirea din apel (pasul 4.c) se extrag, dar se inlocuiesc cu valorile curente ale respectivilor parametrii, (deci memorarea lor este inutila).

Sa consideram de exemplu calculul combinarilor:

/ 0 daca m>n;

comb(n,m)= - 1 daca n=0;

comb(n-1,m)+comb(n-1,m-1);

astfel :

int comb(int n, int m)

Deoarece sunt doua apeluri ale functiei in cadrul aceleiasi instructiuni vom introduce o variabila auxiliara pentru a avea cite un apel pentru o instructiune

int comb(int n,int m)

}

Probleme propuse

1) Sa se scrie o procedura recursiva si programul aferent care sa converteasca un numar intreg "n" intr-un sir de caractere memorat intr-un vector.

2) Sa se scrie o procedura recursiva si programul aferent pentru inversarea caracterelor unui sir alfanumeric memorat intr-un vector. Sirul inversat se va gasi in acelasi vector de intrare.

3) Sa se scrie cu ajutorul stivei programul care rezolva problema 'turnurilor din Hanoi'.

4) Sa se scrie folosind o functie intii, iar apoi cu ajutorul stivei programul pentru calculul functiei lui Ackermann:

ac(m,n)= n+1, daca m=0;

ac(m-1,1), daca n=0;

ac(m-1,ac(m,n-1)) altfel

5) Fie A un masiv de tip real cu I si N doi intregi pozitivi. Se defineste functia :

/ A[ I ] daca I=N

M(A, I, N) =

max( M(A,I+1,N), A[I]) daca I<N

a) Sa se afle M(A, I, N) daca I=1, N=6 si A=[ 3.2; -5.0; 14.6; 7.8; 0.6; 3.2 ];

b) Sa se scrie o functie recursiva pentru MAX.

6) Fie A un masiv de tip real cu I si N doi intregi pozitivi. Se defineste functia:

/ A[ I ] daca I=N

M(A, I, N) =

max(M(A,I,|(I+N)/2|), M(A,|(I+N)/2|+1,N)) daca I<N;

unde |(I+N)/2| inseamna impartire intreaga.

a) Sa se gaseasca valorile pentru M(A, I, N) daca I=1, N=6 si A ia valori ca in exercitiul anterior;

b) Sa se scrie o functie recursiva pentru MAX.

7) Se marcheaza N puncte distincte pe circumferinta unui cerc. Se pune problema: cite unghiuri pot fi desenate astfel incit laturile ungiurilui sa se sprijine pe trei din cel N puncte?

8) Se considera N puncte distincte ca in exercitiul anterior. Se pune problema: in cite moduri pot fi selectate K puncte distincte din cele N puncte date?

9) Se da o permutare a numerelor 1, 2, 3, , n. Fie N numarul de intregi care il depasesc pe 'i'.

Exemplu: N1=2; N2=3; N3=1; N4=4.

Sa se scrie o procedura care va efectua permutari si care va tipari numerele N1 , N2 , , Nn pentru fiecare permutare.

10) Se presupune ca este data o lista dublu legata L. Sa se scrie o procedura recursiva pentru inversarea listei L.

11) Sa se scrie o procedura recursiva care determina daca doua liste simplu legate sint identice. Aceasta inseamna ca ele trebuie sa aiba aceeasi structura si aceleasi date in cimpurile corespunzatoare.