Liste dublu legate

Liste dublu legate

Definitie:

Listele dublu legate sunt tot liste liniare, cu deosebirea ca fiecare element al listei are doua referinte de legatura cu elementele listei: - una spre elementul din stinga si a doua spre elementul din dreapta.

Un element al listei dublu legate va fi ca si in cazul listelor simplu legate de tipul articol (inregistrare, structura), in care vor exista cel putin doua cimpuri de tip referinta (pointer) pentru legarea elementului in lista, un cimp de identificare KEY (cheie de identificare) si un cimp cu informatia utila.

Putem defini spre exemplu:

typedef struct listad

plistad;

unde

key - este cimpul cheii de identificare

inf    - este cimpul informatiei utile atasate elementului

left,right - sunt pointeri de legatura spre stinga, respectiv spre dreapta in lista.

Grafic, un element al listei dublu inlantuite se poate reprezenta:

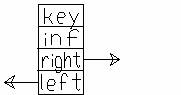
Putem defini acum primul si ultimul element al unei liste dublu inlantuite. Primul element este cel care are cimpul 'left' incarcat cu valoarea NIL, iar ultimul element are a NIL ca valoare a cimpului 'right'.

Reprezentarea grafica a unei liste dublu inlantuite:

In reprezentarea grafica putem renunta la cimpurile de informatii interesindu-ne direct legarea elementelor:

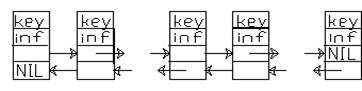
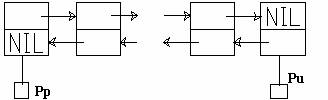
Se observa ca pentru completa definire a listei este nevoie de doua variabile referinta, una care sa memoreze adresa primului element (notata 'pp') si una care sa memoreze adresa ultimului element (notata 'pu').

Parcurgerea listelor dublu inlantuite

Parcurgerea totala a listei (traversarea ei) se face ca si in cazul listei simplu inlantuite atunci cind este nevoie sa se efectueze o anumita actiune asupra tuturor elementelor sale. In acest caz insa traversarea se poate face de la stinga la dreapta, sau de la dreapta la stinga.

Traversarea stinga-dreapta

p=pp;

while (p->right!=NULL)

Traversarea dreapta-stinga :

p=pu;

while (p->left!=NULL)

Parcurgerea partiala se face atunci cind o actiune trebuie sa se produca doar asupra unui element specificat prin cheia sa. In acest fel se face cautarea elementului cu o cheie precizata de la stinga sau de la dreapta urmind ca ulterior sa se execute actiunea asupra elementului cautat.

Vom da un algoritm doar pentru cautarea incepind cu primul element:

p=pp;

gasit=0;

while (p!=NULL && !gasit)

if (p->key==x) gasit=1;

else p=p->right;

(actiune asupra elementului);

In acest caz daca se iese cu gasit=1 atunci pointerul arata elementul cautat.

Eliminarea unui element al listei

Eliminarea unui element al listei dublu inlantuite se face prin modificarea piointerilor 'left' si 'right' al elementelor adiacente acestuia.

Cazuri particulare sunt acelea cind se doreste eliminarea primului, respectiv ultimului element, cind trebuie modificate valorile pointerilor 'pp' respectiv 'pu '.

a) Eliminarea primului element

Grafic:

Se observa ca 'pp' trebuie sa indice spre al doilea element (care devine primul) iar cimpul 'left' al acestuia trebuie sa aiba valoarea NIL.

Algoritmul:

pp->right->left=NULL;

pp=pp->right;

b)Eliminarea ultimului element

Grafic:

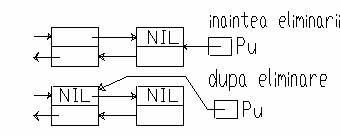
Algoritmul este asemanator:

pu->left->right=NULL;

pu=pu->left;

c) Eliminarea unui element intermediar

Grafic:

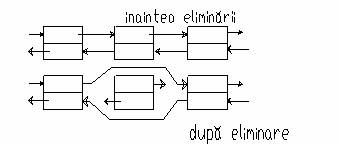
Algoritmul presupune ca inainte a fost cautat si identificat elementul ce trebuie eliminat. Pointerul 'p' contine adresa ecestuia:

p->left->right=p->right;

p->right->left=p->left;

Inserarea unui element in lista

Ca si in cazul eliminarii, actiunile intreprinse pentru inserarea unui element depind de pozitia unde se insereaza elementul: ca primul element al listei, ca ultimul element al listei sau in interiorul listei, dupa un element specificat.

Actiunile pentru inserare cuprind alocarea zonei de memorie pentru elementul respectiv, incarcarea campurilor cu informatii si modificarea legaturilor elementelor.

a)Inserarea unui prim element

Grafic:

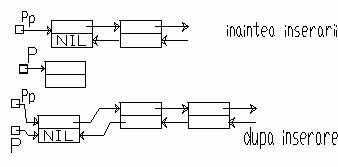
Algoritmul:

p=(plistad *)malloc(sizeof(plistad));

p->left=NULL;

p->right=pp;

pp->left=p;

pp=p;

b)Inserarea unui ultim element

Grafic:

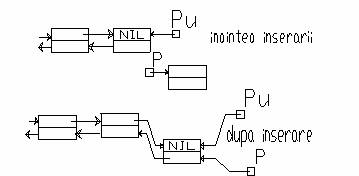
Algoritmul:

p=(plistad *)malloc(sizeof(plistad));

p->right=NULL;

p->left=pu;

pu->right=p;

pu=p;

c)Inserarea unui element interior listei

Inserarea unui element interior listei se poate face inaintea unui element specificat, sau dupa acesta. Elementul se presupune ca a fost cautat dupa cheia de identificare si pointerul 'p' contine adresa acestuia.

Vom exemplifica doar inserarea unui element inaintea unuia specificat, varianta a doua fiind similara.

Grafic:

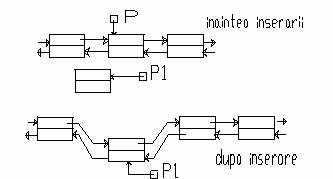
Algoritmul:

p1=(plistad *)malloc(sizeof(plistad));

p1->right=p;

p1->left=p->left;

p->left->right=p1;

p->left=p1;

Crearea listelor dublu inlantuite

Ca si la listele simplu inlantuite, crearea listelor dublu inlantuite se poate face de la stinga la dreapta, sau de la dreapta la stinga, in ambele cazuri intii se genereaza un element si apoi se insereaza la dreapta, sau la stinga acestuia noi elemente.

a) Crearea listei incepind cu primul element

p=(plistad *)malloc(sizeof(plistad));

p->left=NULL;

p->right=NULL;

pp=p;

pu=p;

do

while (ch=='y');

b)Crearea unei liste incepind cu ultimul element

p=(plistad *)malloc(sizeof(plistad));

p->left=NULL;

p->right=NULL;

pp=p;

pu=p;

do

while (ch=='y');

Observatie:

S-a considerat ca oprirea generarii listei este data de la tastatura, cand variabila de tip caracter 'ch' ia valoarea 'y'.

Problema rezolvata

Sa se creeze o lista liniara dublu inlantuita plecand de la un vector de numere intregi si sa se ordoneze apoi in ordine crescatoare elementele acesteia.

Algoritmul de ordonare foloseste un semafor 'q' care indica dupa mai multe parcurgeri daca mai exista o pereche de elemente (a_k, a_k+1), astfel incat a_k>a_k+1

Cand se intalneste asemenea situatie, se face si interschimbarea respectivelor elemente.

Va trebui sa refacem urmatoarele legaturi pentru interschimbare:

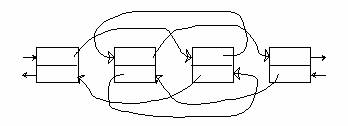
Vom nota cu 'p' pointerul spre a_k si p1=p->right.

#include <stdio.h>

#include <stdlib.h>

typedef struct list

plist;

plist *p, *p1, *p2, *pu, *pp;

int a, i, j, q;

char    ch;

void main()

else

printf('n');

printf('Mai sunt numere ?[Y/N]');

do while (!(ch=='Y' || ch=='y' || ch=='N' || ch=='n'));

} while (!(ch=='N' || ch=='n'));

p = pp;

p1 = p->right;

if ((p1->right == NULL) && (p->r2 > p1->r2))

else

else

if (p1 == pu)

else

p = p->right;

p1 = p1->right;

}

p = pp;

p1 = p->right; } while (!(q == 0));

p = pp;

}

printf('numerele in ordine crescatoare:n');

while (p != NULL)

}

Observatie:

S-au luat in considerare si cazurile cand 'p' respectiv 'p1' sunt 'pp' respectiv 'pu'. S-a simplificat algoritmul de creeare a unei liste dublu inlantuite incepand cu primul element inglobandu-se in ciclu si crearea primului element:

pp=NULL;    crearea listei vide

pu=NULL;

do

else crearea celorlalte elemente

} while !(..); conditie de terminare

Asemanator se poate scrie un algoritm si pentru crearea listei incepand cu ultimul element.

Probleme propuse

1. Sa se scrie un program care creaza o lista dublu inlantuita plecand de la un vector de numere reale si realizeaza apoi inversarea elementelor listei.

2. Aceeasi problema si pentru problema numarul 4 de la problemele propuse la liste liniare simplu legate, problema care se refera insa la liste dublu legate.

3. Se considera o lista dublu inlantuita ale carei noduri sint alocate ca elemente ale unui vector avind "m" componente numerotate de la 1 la m. Fiecare nod al listei are doua cimpuri ''info'' si ''link''. Cimpul ''link'' este egal cu suma modulo 2 bit cu bit a echivalentilor binari ai nodurilor precedent, respectiv succesiv ai nodului curent. Daca s-ar considera ca fiecare nod ar avea doua cimpuri ipotetice left, respectv right care indica spre elementul din stinga, respectiv dreapta al listei, atunci link=(left+right) mod 2. Cunoscind capetele "l" si "r" ale listei si faptul ca elementul cel mai din stinga are cimpul ipotetic left=0 si cel mai din dreapta cimpul ipotetic right=0 sa se scrie doua proceduri care traverseaza si afiseaza informatia cimpurilor info de la stinga la drepta, respectiv de la drepta la stinga.

4. Sa se transforme o lista liniara simplu legata intr-o lista liniara dublu legata.

5. Sa se inverseze legaturile intr-o lista liniara dublu legata.

6. Pentru evidenta angajatilor unei intreprinderi trebuie gestionata o lista dublu inlantuita, fiecare nod al listei memorind informatiile referitoare la un anumit angajat, care cuprind: numele si prenumele angajatului, numarul de ordine, codul departamentului (1 caracter), numarul de ore lucrate saptaminal, salariul angajatului. Sa se scrie proceduri pentru:

a) Crearea listei angajatilor;

b) Afisarea listei angajatilor;

c) Eliminarea din lista a acelor angajati care lucreaza mai putin de 40 de ore pe saptamina;

d) Inserarea unui nou angajat in lista astfel incit lista sa se mentina sortata dupa numarul de ordine al angajatilor.

Se presupune ca lista angajatilor are un nod antet care memoreaza numarul de noduri ale listei si pointeaza catre nodul corespunzator primului angajat din lista.

7. Sa se scrie o procedura care determina inversa, pe loc, a unei liste liniare dublu legate.

8. Sa se scrie o procedura care concateneaza doua liste liniare dublu legate intr-o a treia lista liniara simplu legata.

9. Scrieti o procedura care verifica daca o lista liniara dublu legata contine sau nu elemente care se repeta.

10. Se considera doua liste liniare dublu legate "m" si "l". Scrieti o procedura care testeaza daca elementele lui "m", luate in ordinea in care apar in "m" sint identice cu elementele din inceputul lui "l", luate in ordinea in care apar in "l".

11. Se considera doua liste liniare simplu legate, "m" si "l". Scrieti o procedura care testeaza daca elementele listei "m" sint continute in lista "l", indiferent de ordine

12. Se considera doua liste liniare simplu legate "m" si "l". Scrieti o procedura care testeaza daca "m" este o sublista a lui "l".