CALCULUL CLADIRILOR CU PERETI STRUCTURALI DIN ZIDARIE

CALCULUL CLADIRILOR CU PERETI STRUCTURALI DIN ZIDARIE

1. Principii generale de calcul

(1) Zidaria este un material neomogen, anizotrop si caracterizat de comportare inelastica chiar pentru niveluri reduse de solicitare. Realizarea unui model de calcul care sa ia in considerare toate aceste particularitati si, in acelasi timp, sa poata fi aplicat cu usurinta in proiectarea curenta este practic imposibila.

(2) Pentru proiectarea structurilor cladirilor curente, definite la 1.1 5), determinarea eforturilor si deformatiilor in elementele de zidarie, se poate face utilizand un model de calcul, suficient de precis, bazat pe urmatoarele ipoteze simplificatoare:

i.        zidaria este un material presupus omogen, izotrop si cu raspuns elastic pana in stadiul ultim;

ii.      caracteristicile sectionale ale peretilor de zidarie se determina pentru sectiunea bruta (nefisurata);

iii.    pentru aplicatiile curente, rezultatele calculelor obtinute prin modelele bazate pe ipotezele i si ii se afecteaza cu factori de corectie stabiliti astfel incat sa se obtina o concordanta cat mai buna cu datele rezultate din incercari.

(3) Modelul de calcul pentru determinarea eforturilor sectionale si a rezistentei de proiectare a peretilor (elementelor) de zidarie trebuie sa reprezinte in mod adecvat proprietatile de rezistenta, de rigiditate si de ductilitate ale intregului sistem structural.

2. Calculul structurilor la incarcari verticale

2.1. Modelul de calcul pentru incarcari verticale

(1) Peretii structurali din zidarie sunt elemente verticale ale suprastructurii cladirii care preiau, in principal, incarcarile de tip gravitational aduse de plansee si le transmit terenului de fundare prin intermediul infrastructurii.

(2) Pentru calculul sub actiunea incarcarilor verticale, peretii structurali sunt considerati console rezemate la nivelul planseului peste subsol (in cazul cladirilor cu subsol) sau la fata superioara a fundatiilor (in cazul cladirilor fara subsol).

(3) Peretii din zidarie pot fi solicitati, simultan cu incarcarile verticale, si de incarcari orizontale, cu caracter local, care actioneaza perpendicular pe planul peretelui:

• incarcari din actiunea cutremurului, pentru toti peretii structurali si nestructurali;
• incarcari date de presiunea vantului, pentru peretii exteriori din elevatia cladirii;
• incarcari date de impingerea pamantului, pentru peretii de contur de la subsol (aceste incarcari vor include si eventualele suprasarcini pe terenul din imediata vecinatate a cladirii);
• forte datorate impingerilor produse de bolti, arce, sau sarpante;
• incarcari de exploatare (mobiler sau echipamente/instalatii suspendate pe console, impingerea oamenilor in spatii aglomerate, etc).

(4) Modelul de calcul trebuie sa tina seama de:

• particularitatile modului de aplicare a incarcarilor verticale;

• excentricitatile corespunzatoare momentelor incovoietoare produse de incarcarile orizontale perpendiculare pe planul peretelui mentionate la (3);
• zveltetea peretelui.

2.2. Metode de calcul pentru incarcari verticale

2.2.1.Determinarea fortelor axiale de compresiune in peretii structurali

(1) Forta axiala de compresiune intr-o sectiune de calcul a unui perete structural se compune din:

• suma incarcarilor aplicate pe zonele aferente ale planseelor aflate peste nivelul sectiunii de calcul;
• greutatea proprie a portiunii de perete aflata peste nivelul sectiunii de calcul

(2) In cazul planseelor alcatuite din placi de beton armat care transmit incarcarile pe doua directii, indiferent de tehnologia de realizare (monolit, prefabricat din panouri mari, mixt- predale cu suprabetonare), peretii preiau incarcarile aplicate pe portiunile de placa aferente, determinate de bisectoarele unghiurilor formate de laturile placilor (l₁ l₂).

Aceste incarcari se considera uniform distribuite pe lungimea peretelui respectiv la care, in cazul peretilor cu goluri de usi si/sau ferestre, se adauga cate din latimea golurilor care marginesc peretele.

In cazul peretilor in forma complexa T,L,I, se considera ca, prin legatura creata prin teserea zidariei sau prin stalpisorii de beton de la intersectii sau ramificatii, se realizeaza o distributie uniforma a intensitatii fortelor de compresiune pe intreaga suprafata a peretelui (figura 1a)

(3) In cazul planseelor de beton armat care descarca pe o singura directie (fasii pline sau cu goluri) sau in cazul planseelor cu grinzi metalice sau din lemn, se considera ca incarcarile se transmit atat peretilor pe care acestea reazema cat si zonelor active la compresiune ale peretilor transversali (talpilor) (figura 1b).

Lungimea zonelor active ale talpilor se determina conform 3.1 3).

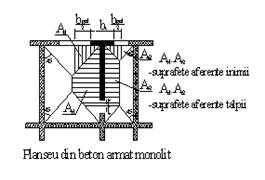
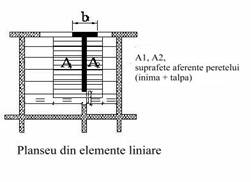
Figura 1

Incarcari verticale pe peretii structurali date de plansee

(a) Planseu din beton armat monolit (b) Planseu din elemente liniare (beton, otel, lemn)

(4) Pentru incarcarile concentrate sau pentru incarcarile distribuite aplicate numai pe anumite zone ale peretelui se admite ca repartizarea eforturilor in perete se face dupa linii inclinate la 30^o fata de verticala ca in figura 2a . In cazul peretilor cu goluri traseul de descarcare se modifica conform figurii 2b.

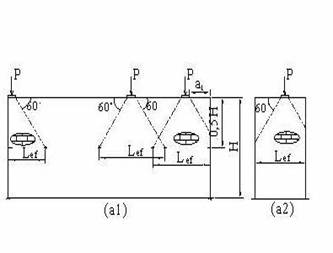
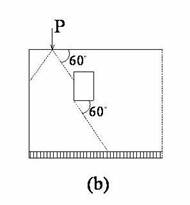
Figura 2

Incarcari verticale concentrate pe peretii structurali

(a) Cazul curent (b) Devierea traseului de descarcare in vecinatatea golurilor

(5) In situatiile curente se admite ca rezultanta incarcarilor verticale se aplica in centrul de greutate al sectiunii active a peretelui. In cazul in care distanta dintre centrul de greutate al incarcarilor verticale si centrul de greutate al sectiunii orizontale a peretelui este relativ importanta (cazul cladirilor cu balcoane/bowindow-uri cu deschideri mari, dispuse pe o singura latura a cladirii, de exemplu) si daca efectul excentricitatilor nu se echilibreaza pe ansamblul structurii, este necesar sa se evalueze eforturile suplimentare rezultate din aceasta situatie.

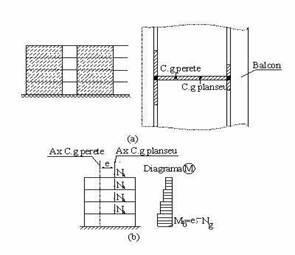
Figura 3

Incarcari verticale excentrice pe peretii structurali

2.2.2. Determinarea excentricitatilor de aplicare a incarcarilor verticale

(1) In cladirile din zidarie, incarcarile verticale aduse de plansee, considerate, de regula, ca se transmit catre fundatii ca forte axiale in pereti, sunt asociate, in realitate, unor excentricitati care provin din mai multe surse:

alcatuirea constructiva a structurii, care poate implica deviatii ale fluxului fortelor verticale de la un nivel la altul;

existenta unor imperfectiuni de executie, inevitabile in anumite limite - in practica curenta, in ceea ce priveste geometria structurii, omogenitatea materialelor structurii, pozitiile relative ale subansamblurilor/elementelor structurii;

efectele unor incarcari cu caracter local, de intensitate mai mica, dar nu neglijabila, decat cea a incarcarilor permanente sau a fortelor seismice.

(2) Efectele acestor excentricitati se concretizeaza in momente incovoietoare suplimentare, care solicita peretele perpendicular pe planul de rezistenta/rigiditate maxime si care, in anumite conditii, pot periclita rezistenta si stabilitatea peretelui.

(3) In calculele curente de dimensionare/verificare, efectele excentricitatilor, din toate categoriile mentionate mai sus, se introduc prin coeficienti de reducere a capacitatii teoretice de rezistenta calculata pentru incarcarile 'ideal' axiale.

2.2.2.1. Excentricitati provenite din alcatuirea structurii.

(1) Excentricitatile provenite din alcatuirea structurii se produc in zonele in care se produce transferul fortelor verticale de la un etaj la altul si se datoreaza :

• suprapunerii excentrice pe verticala a peretilor la etajele adiacente;
• rezemarii excentrice a planseelor pe perete;
• rezemarii pe perete a unor plansee cu deschideri si incarcari diferite.

(2) Momentele incovoietoare rezultate din excentricitatile mentionate la (1) variaza liniar pe inaltimea peretelui intre valoarea maxima la partea superioara a peretelui si zero, la partea inferioara a peretelui

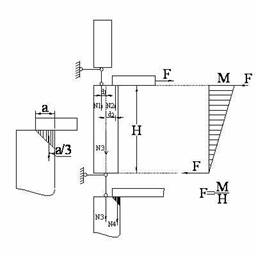
Figura 4

Excentricitati provenite din alcatuirea structurii

(3) Excentricitatea datorata tuturor incarcarilor verticale aplicate peste nivelul de calcul, provenita din modul de alcatuire a structurii, se determina cu relatia:

(1)

unde:

• N₁ incarcarea transmisa de peretele de la etajul superior;
• d₁ excentricitatea cu care este aplicata incarcarea N₁;
• N₂ - incarcarile aduse de planseul/planseele care reazema direct pe perete;
• d₂ excentricitatile cu care sunt aplicate incarcarile N₂.

2.2.2.2. Excentricitati datorate imperfectiunilor de executie (excentricitate

accidentala)

(1) Excentricitatea accidentala a fortelor verticale (e_a) poate fi cauzata de urmatoarele categorii de imperfectiuni de executie:

• deplasarea relativa a planurilor mediane ale peretilor de la doua niveluri adiacente;
• abaterile de la valoarea nominala a grosimii peretilor;

abaterile de la pozitia verticala a peretelui;

• neomogenitatea materialelor.

(2) In calcule, excentricitatea accidentala se va introduce cu cea mai mare dintre valorile:

(2a)

(2b)

unde:

t - grosimea peretelui;

h_et - inaltimea etajului.

2.2.2.3. Excentricitatea datorata momentelor incovoietoare produse de fortele

orizontale perpendiculare pe planul peretelui

(1) Pentru determinarea excentricitatii de calcul, momentele incovoietoare M_hm(i) produse de fortele orizontale din vant sau cutremur pot fi calculate simplificat cu relatia (8) de la 4.2.

(2) Excentricitatea fortei verticale corespunzatoare momentelor M_hm(i) este data de relatia

(3)

unde

N₁ - incarcarea transmisa de peretele superior;

SN₂ - suma reactiunilor planseelor care reazema pe peretele care se verifica

3. Calculul structurilor din zidarie la incarcari orizontale.

(1) Tinand seama inaltimea redusa a cladirilor din zidarie pentru care, in toate zonele seismice, fortele provenite din actiunea vantului sunt inferioare fortelor seismice, verificarea structurilor din zidarie la actiunea vantului in planul peretilor nu este necesara.

(2) Incarcarile din vant vor fi luate in considerare numai pentru:

calculul excentricitatii fortei verticale datorate momentelor incovoietoare date de actiunea vantului perpendicular pe fatada (conform 2.2.2.3)

calculul sarpantelor;

verificarea rezistentei si rigiditatii fatadelor din sticla de mari dimensiuni.

(3) In cazul cladirilor etajate din zidarie care constituie obiectul prezentului Cod se vor lua in considerare numai fortele orizontale provenite din actiunea seismica. Pentru cladirile tip 'sala/hala' componenta verticala a actiunii seismice se va lua in calcul pentru structura acoperisului in conditiile prevazute in Codul P100-1/200

3.1. Modelul de calcul pentru forte seismice orizontale.

(1) Suprastructura cladirii se va modela prin subansambluri structurale verticale dispuse pe directiile principale, constituite din pereti plini sau cu goluri, legate prin plansee orizontale.

(2) Sectiunea de incastrare a ansamblului peretilor structurali pentru calculul la forte orizontale (in raport cu care se defineste numarul de niveluri n_niv) se va lua:

la nivelul superior al soclurilor, in cazul cladirilor fara subsol;

la planseul peste subsol, la cladirile cu pereti desi (sistem fagure) sau la cele cu pereti rari (sistem celular) la care s-au prevazut pereti suplimentari in subsol conform recomandarii de la 5.4.3 (4);

peste nivelul fundatiilor la cladirile cu pereti rari, daca nu se prevad pereti suplimentari in subsol conform recomandarii de la 5.4.3.(4).

(3) Peretii activi de pe fiecare directie a cladirii, participanti la preluarea fortelor seismice se delimiteaza considerand, in cazul sectiunilor compuse (L,T, I), lungimile talpilor active egale cu grosimea peretelui la care se adauga, de fiecare parte a inimii, cea mai mica dintre valorile:

In zona comprimata:

h_tot/5 - unde h_tot este inaltimea totala a peretelui structural considerat;

din distanta intre peretii structurali care sunt legati cu un perete transversal;

distanta pana la capatul peretelui transversal de fiecare parte a inimii;

din inaltimea libera a peretelui (h).

In zona intinsa:

din inaltimea libera a peretelui (h);

distanta pana la capatul peretelui transversal de fiecare parte a inimii.

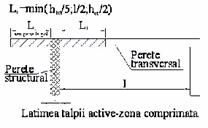
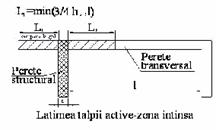
Figura 5

Dimensiunile talpilor active

(a) Talpa comprimata (b) Talpa intinsa

(4) Golurile din talpi cu dimensiunea maxima h/4 pot fi neglijate iar golurile cu dimensiune > h/4 vor fi considerate margini ale talpii.

(5) Pentru determinarea eforturilor seismice de proiectare din peretii structurali se utilizeaza modele de calcul care descriu comportarea structurii la actiunea dinamica a cutremurului.

In acest scop, modelul structural trebuie sa schematizeze cat mai exact urmatoarele elemente:

alcatuirea generala structurii:

geometria de ansamblu si a fiecarui subansamblu in parte;

legaturile intre subansamblurile structurale si legaturile dintre componentele fiecarui subansamblu;

proprietatile mecanice relevante ale materialelor;

distributia maselor de nivel, in plan si pe inaltimea cladirii;

caracteristicile de rigiditate stabilite conform (8) sau (9) si capacitatea de amortizare.

(6) Constructiile etajate, cu plansee din beton armat rigide in planul lor (conform 5.3.1.), se modeleaza ca sisteme elastice cu trei grade de libertate dinamica (doua translatii orizontale si o rotire in jurul axei verticale) pentru fiecare nivel.

(7) In cazul cladirilor cu regularitate structurala, pozitiile 1 si 2 din tabelul 5.1, pentru determinarea valorilor eforturilor seismice de proiectare care actioneaza in planul fiecarui perete, calculul se poate face considerand doua modele plane constituite, fiecare, din totalitatea peretilor structurali de pe una din directiile principale. In acest caz, pentru cladirile cu plansee rigide in plan orizontal, fiecare model plan constituie un sistem dinamic elastic cu un singur grad de liberate la fiecare nivel (translatie in planul peretilor).

Se considera ca forta seismica actioneaza succesiv si independent pe fiecare din directiile principale iar raspunsurile seismice astfel obtinute nu se suprapun. Eventualele eforturi suplimentare provenite din efectele torsiunii de ansamblu pot fi evaluate prin procedee simplificate si adaugate eforturilor determinate pe fiecare din modelele plane (acest procedeu este dat in Codul P100-1/2006, art.4.5.3.2.4.)

In cazul cladirilor la care peretii nu sunt dispusi pe doua directii ortogonale in plan fortele seismice vor fi considerate ca actionand pe directiile principale ale sistemului de pereti.

(8) Pentru cladirile care nu prezinta regularitate structurala, pozitiile 3 si 4 din tabelul 5.1, modelul de calcul folosit va tine seama de caracterul spatial al actiunii seismice si al raspunsului structurii.

(9) Rigiditatea elementelor structurale trebuie sa fie evaluata luand in considerare atat deformabilitatea din incovoiere cat si cea din forfecare si, daca este cazul, deformabilitatea axiala. Pentru calcule se poate folosi rigiditatea elastica a zidariei nefisurate.

(10) Daca se urmareste o evaluare mai precisa a deplasarilor, in calcule se poate folosi rigiditatea zidariei fisurate pentru a tine seama de influenta fisurarii asupra deformabilitatii. In absenta unor evaluari mai exacte, rigiditatile de incovoiere si de forfecare ale zidariei fisurate vor fi luate egale cu jumatate din rigiditatea elastica a sectiunii intregi de zidarie nefisurata.

(11) Rigiditatea riglelor de cuplare din beton armat se va lua in calcul cu valorile folosite, in mod curent, pentru calculul cladirilor cu pereti structurali din beton armat.

(12) In modelul de calcul pentru peretii cu goluri din zidarie nearmata nu se va tine seama de efectul riglelor de cuplare. Acestea vor fi armate constructiv, dar astfel incat

cedarea riglei prin incovoiere sa preceada:

cedarea riglei prin forta taietoare;

cedarea reazemului (montantului) prin zdrobirea locala a zidariei.

3.2. Metode de calcul pentru forte orizontale

(1) Pentru calculul cladirilor din zidarie la incarcari orizontale, provenite in situatiile curente din actiunea seismica, se folosesc metode simplificate de calcul in care se admite comportarea liniar elastica a materialelor. In paragrafele urmatoare se dau precizari pentru folosirea acestor metode in concordanta cu prevederile Codului P 100-1/200

(2) Pentru evaluarea si validarea unor alcatuiri arhitectural-structurale care nu respecta in totalitate recomandarile din Cap.5 al Codului pot fi folosite procedee de calcul care iau in considerare comportarea postelastica a peretilor structurali de zidarie.

Aplicarea acestor metode implica, in prealabil, dimensionarea completa a structurii prin procedee de calcul elastic (inclusiv stabilirea armarilor din stalpisori, centuri, rigle de cuplare si din rosturile orizontale ale zidariei).

(3) Procedeul de calcul static neliniar (calcul 'biografic') urmareste, pe masura sporirii incarcarilor laterale, evolutia nivelurilor de solicitare atinse de peretii structurali (montanti si, dupa caz, rigle de cuplare) pana la iesirea succesiva din lucru a acestora.

Aplicarea procedeului, fara suportul unui program de calcul specializat, este dificila deoarece implica modificarea schemei statice a ansamblului dupa iesirea din lucru a fiecarui perete. Capacitatea ultima a structurii se considera atinsa atunci cand s-a produs articularea plastica a montantilor care, impreuna, preiau cel putin 15% din forta seismica totala capabila a cladirii.

(4) Folosirea procedeelor de calcul dinamic neliniar nu este justificata pentru cladirile cu pereti structurali din zidarie.

3.2.1. Calculul fortelor seismice orizontale pentru ansamblul cladirii

(1) Pentru cladirile cu regularitate structurala (pozitiile 1 si 2 din tabelul 5.1) calculul fortelor seismice pentru cladire se va face cu metoda fortelor laterale asociate modului de vibratie fundamental descrisa in paragraful 4.5.3.2.2. din Codul P 100-1/200

In aceasta metoda, caracterul dinamic al actiunii seismice este reprezentat in mod simplificat prin forte statice (metoda statica echivalenta).

Distributia fortei seismice totale pe inaltimea cladirii se va face, considerand comportarea elastica a structurii, conform paragrafului 4.5.3.2.3. din P100-1/2006 iar efectele torsiunii de ansamblu vor fi luate in considerare conform paragrafului 4.5.3.2.4. din P100-1/200

(2) In cazul cladirilor cu regularitate structurala care au peste planseul ultimului nivel proeminente (constructii de mici dimensiuni) care se incadreaza in conditiile de la 5.1.5 9), calculul fortelor seismice se va conduce dupa cum urmeaza:

i.        Forta taietoare de baza (F_b) pentru intreaga cladire (cu masa totala m) se va calcula ca la (1) considerand ca masa proeminentei (m_p) se adauga masei ultimului nivel.

ii.      Forta taietoare de baza (F_p) aferenta masei proeminentei (m_p) se va determina considerand ca aceasta este o constructie independenta, cu un singur grad de libertate, asezata pe teren, cu relatia

(4)

(3) Pentru cladirile care nu au regularitate structurala (pozitiile 3 si 4 din tabelul 5.1), fortele seismice pentru ansamblul cladirii se vor determina cu metoda de 'calcul modal cu spectre de raspuns' descrisa in paragraful 4.5.3.3. din Codul P 100-1/200

Daca aceste cladiri au o proeminenta la ultimul etaj, structura acesteia va fi introdusa in modelul general de calcul pentru cladirea principala, chiar daca se incadreaza in conditiile de la 5.1.5.

(4) Pentru toate tipurile de cladiri, factorii de comportare 'q' pentru structurile de zidarie, se stabilesc in functie de tipul zidariei si de grupa de regularitate a constructiei conform Codului P 100-1/200

(5) Pentru calculul fortelor seismice se va tine seama de coeficientii de suprarezistenta (a_u/a₁) ai structurilor din zidarie definiti in Codul P100-1/2006, care au in vedere, rezervele de rezistenta structurala a cladirilor etajate cu pereti structurali din zidarie. Aceste rezerve provin, de regula, din mai multe surse: redundanta sistemului structural (articulatiile plastice de la baza montantilor nu se produc simultan), suprarezistenta armaturilor, efectele favorabile ale unor masuri constructive, etc.

(6) In cazul peretilor cu goluri de usi si/sau ferestre, plinurile de zidarie (sub/peste nivelul planseului-buiandrugi si/sau parapeti) pot fi considerate, in modelul de calcul, ca grinzi de cuplare intre doua elemente de perete daca acestea sunt tesute efectiv cu montantii alaturati si daca sunt legate atat cu centura planseului cat si cu buiandrugul de beton armat de sub zidarie (daca acesta este separat de centura planseului).

(7) Daca sunt indeplinite conditiile de la (6), sau daca riglele de cuplare sunt integral din beton armat, se poate folosi un calcul de cadru pentru determinarea efectelor actiunilor verticale si seismice in montanti si in grinzile de cuplare.

3.2.2. Calculul eforturilor sectionale in peretii structurali

(1) Distributia fortei totale intre peretii structurali rezulta din modelul de calcul.

(2) Pentru constructiile cu plansee rigide in plan orizontal, forta seismica de proiectare pentru ansamblul constructiei, calculata conform 3.2.1., se distribuie peretilor structurali proportional cu rigiditatea laterala a fiecaruia determinata pe baza principiilor din Codul P100-1/200

(3) Pentru constructiile cu plansee cu rigiditate nesemnificativa in plan orizontal, forta seismica de proiectare pentru ansamblul constructiei, calculata conform 3.2.1., se distribuie peretilor structurali proportional cu masa aferenta fiecaruia.

(4) Fortele taietoare de baza pentru peretii structurali determinate prin calculul liniar elastic, conform 3.1 8), pot fi redistribuite intre peretii de pe aceiasi directie, cu conditia ca echilibrul global sa fie satisfacut si ca forta taietoare in oricare perete sa nu fie redusa/sporita cu mai mult de 20%.

(5) In cazul peretilor cu sectiune compusa (I,T,L) forta de lunecare verticala in sectiunea dintre inima si talpa (L_v,et) se calculeaza, pentru un etaj, cu relatia :

(5)

unde

DM = M_inf - M_sup cu:

M_inf - momentul incovoietor de proiectare in sectiunea de la baza etajului pentru care se calculeaza lunecarea;

M_sup - idem, in sectiunea de la baza etajului superior;

S_i - momentul static al sectiunii ideale a talpii fata de centrul de greutate al

sectiunii ideale a peretelui;

I_i - momentul de inertie al sectiunii ideale a peretelui.

Caracteristicile geometrice ale sectiunii ideale (S_i si I_i) se determina folosind coeficientul de echivalenta n_ech dat de relatia (24).

(6) Pentru determinarea eforturilor sectionale (N,M,V) in elementele structurii si pentru determinarea deplasarilor laterale ale acesteia poate fi folosit orice program de calcul bazat pe principiile recunoscute ale mecanicii structurilor.

3.2.3. Calculul deformatiilor si deplasarilor laterale in planul peretelui

(1) Calculul deformatiilor si deplasarilor laterale ale peretilor de zidarie sub efectul fortelor laterale aplicate in planul lor se va efectua tinand seama de deformatiile specifice de incovoiere si de forfecare si, daca sunt relevante, de deformatiile specifice axiale.

(2) Calculul deformatiilor si deplasarilor laterale se va face cu relatiile curente ale staticii constructiilor, tinand seama de conditiile de fixare de la extremitatile peretelui.

(3) Pentru calculul deformatiilor si deplasarilor laterale ale peretilor de zidarie sub actiunea fortelor seismice de proiectare se vor folosi:

pentru zidaria nearmata (ZNA) :

caracteristicile geometrice ale sectiunii nefisurate de zidarie;

din valoarea modulul de elasticitate secant de scurta durata al zidariei (E_z) determinat conform prevederilor de la 4.1.2.2.1. (2) sau cu valoarea data in tabelul 4.9, in functie de rezistenta caracteristica la compresiune a zidariei (f_k);

din valoarea modulului de elasticitate transversal calculat cu relatia (4.9);

• pentru zidaria confinata (ZC) si pentru zidaria cu inima armata (ZIA):

caracteristicile geometrice ale sectiunii nefisurate de zidarie si de beton;

din valoarea modulului de elasticitate longitudinal echivalent, de scurta durata, (E_ZC(ZIA)) calculat cu relatia (4.7);

din valoarea modulului de elasticitate transversal echivalent (G_ZC(ZIA)) calculat cu relatia (4.10).

NOTA. In cazul peretilor cu sectiune compusa (L,T,I), dimensiunile talpilor introduse in calculul caracteristicilor geometrice se vor lua conform 3.1.(3).

4. Calculul peretilor structurali si nestructurali la incarcari orizontale

perpendiculare pe planul peretelui.

(1) Incarcarile orizontale care pot actiona perpendicular pe planul peretilor din zidarie sunt cele mentionate la 2.1 3).

(2) Valorile de proiectare ale fiecarei categorii de forte care actioneaza perpendicular pe planul peretelui se vor lua din reglementarile specifice respective.

4.1. Modele de calcul pentru incarcari perpendiculare pe planul peretelui

(1) Pentru calculul momentelor incovoietoare sub efectul incarcarilor perpendiculare pe planul lor peretii se modeleaza ca placi elastice rezemate, sus si jos, pe planseele etajului respectiv si, lateral, pe peretii de rigidizare (perpendiculari pe planul peretelui considerat).

(2) In cazul peretilor de subsol, pentru calculul momentului incovoietor dat de impingerea pamantului, peretele va fi considerat articulat sau incastrat la nivelul fundatiei (in functie de rezolvarea constructiva adoptata) si incastrat elastic la nivelul planseului peste subsol.

4.2. Metode de calcul pentru incarcari perpendiculare pe planul peretelui

(1) Pentru panourile de zidarie fara goluri de usi sau ferestre, momentele incovoietoare de proiectare produse de fortele perpendiculare pe planul peretelui (M_Sxd1 si M_Sxd2) pot fi calculate, in absenta unei metode mai exacte (de exemplu, cu elemente finite), folosind relatiile cunoscute din teoria placilor elastice. Conditiile de margine vor fi stabilite in functie de legaturile efective de rezemare/fixare de la extremitatile panourilor.

(2) In cazul panourilor cu goluri, pentru calculul momentelor incovoietoare de proiectare, panourile vor fi divizate in semipanouri care pot fi calculate folosind regulile de la panourile pline asa cum este exemplificat in figura 6

( luand ca document normativ de referinta EN 1996-1-1)

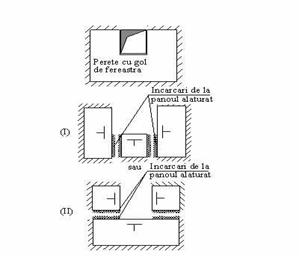
Figura 6

Modele de calcul la forte perpendiculare pe plan pentru peretii cu goluri

(3) Forta seismica de proiectare perpendiculara pe planul peretilor va fi calculata conform Codului P 100-1/2006, cap . Greutatea de calcul a peretelui va include si greutatea in exploatare a mobilierului sau altor echipamente sau instalatii suspendate de perete (de exemplu, rafturi de biblioteca inclusiv cartile, boilere si sisteme de conducte inclusiv apa continuta, etc).

(4) Pentru simplificare, momentele incovoietoare maxime pot fi determinate, neglijand efectul reazemelor laterale, ca pentru o fasie verticala continua in dreptul planseelor. Se accepta ca momentele incovoietoare in dreptul planseelor (M_hi) si la mijlocul inaltimii etajului (M_hm) sunt egale si se vor calcula cu relatia

(6)

unde:

pentru incarcarea orizontala din vant, p_h este forta uniform distribuita, aferenta fasiei respective;

pentru incarcarile orizontale din cutremur, p_h este forta medie pe inaltimea etajului respective calculata conform Codului P 100-1/2006, Cap.10

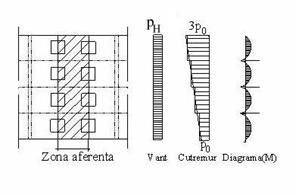
Figura 7

Model simplificat de calcul pentru incarcari perpendiculare pe planul peretelui la cladiri etajate

5. Calculul planseelor

(1) Planseele cladirilor din zidarie se dimensioneaza pentru:

incarcari verticale, permanente si de exploatare;

incarcari orizontale care actioneaza in planul median al planseului.

(2) Proiectarea planseelor din beton armat pentru incarcari verticale se va face luand ca document normativ de referinta STAS 10107/1

(3) Proiectarea planseelor din lemn pentru incarcari verticale se va face luand ca document normativ de referinta NP 019-1997 si NP 005-2003.

(4) Proiectarea planseelor de beton armat la incarcari orizontale are ca scop asigurarea capacitatii de rezistenta si a rigiditatii necesare pentru ca planseul sa poata fi considerat diafragma rigida in plan orizontal.

(5) Verificarea rezistentei si rigiditatii planseelor la forte orizontale este necesara pentru urmatoarele categorii de cladiri din zidarie:

• cladiri etajate cu pereti rari (sistem celular);
• cladiri tip 'sala/hala', pentru planseul de acoperis;
• cladiri etajate cu goluri mari in plansee;
• cladiri cu plansee prefabricate (pentru verificarea capacitatii imbinarilor).

In cazul cladirilor cu pereti desi (sistem fagure) verificarea planseelor din beton armat la forte orizontale nu este necesara.

5.1.Modelul de calcul

(1) La cladirile cu forme simple in plan, care pot fi inscrise, aproximativ, intr-un dreptunghi, pentru calculul eforturilor sectionale (forta taietoare si moment incovoietor) provenite din fortele seismice orizontale, planseul va fi considerat ca grinda continua, rezemata pe peretii structurali. In acest caz calculul eforturilor sectionale in planseu se va face conform 5.2.

(2) Pentru proiectarea planseelor cu alcatuiri complicate (cu forme neregulate si cu goluri relativ mari, cu incarcari concentrate mari, etc) si pentru proiectarea planseelor in structuri cu neregularitati (lipsa de uniformitate) in plan si pe verticala se vor utiliza modelele si metode de calcul care pot sa evidentieze suficient de exact comportarea acestora la incarcari verticale si la cutremur (in particular, efectul rigiditatii planseelor asupra distributiei fortelor seismice intre peretii structurali si efectul cedarii premature a unor pereti).

5.2.Metoda de calcul

(1) In conditiile de la 5.1(1) forta totala de calcul pentru un planseu este egala cu forta seismica aplicata la nivelul respectiv. In mod simplificat, aceasta forta se poate considera distribuita liniar pe lungimea planseului, cu rezultanta trecand prin centrul de rigiditate al structurii de la nivelul respectiv.

In aceasta ipoteza valorile extreme ale fortei p_max/min care actioneaza asupra planseului sunt:

(7)

unde :

• S_niv     - forta seismica de proiectare aplicata la nivelul planseului respectiv;
• d_RG distanta intre centrul de greutate al planseului (G) si centrul de rigiditate (R);

• L dimensiunea cladirii perpendicular pe directia de calcul.

(2) Reactiunea din sectiunea de rezemare a planseului pe un perete structural (F_i) se poate lua proportionala cu suma capacitatilor de rezistenta la forta taietoare a tuturor montantilor peretelui respectiv (SV_Rdi

(8)

unde

• V_R - capacitatea de rezistenta la forta taietoare a cladirii pe directia de calcul.

(3) Momentul incovoietor M si forta taietoare T in planseu se determina din conditiile de echilibru static sub efectul incarcarii p si al reactiunilor F_i.

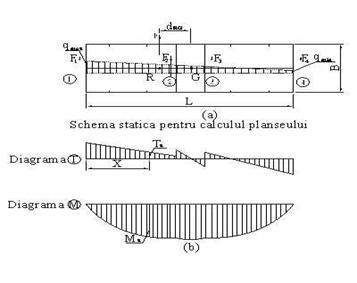
Figura 8

Calculul eforturilor sectionale de proiectare in plansee din incarcari orizontale

(a) Determinarea incarcarii in planul planseului (b) Eforturi sectionale in planseu

(4) In cladirile cu regularitate structurala, care au toate planseele identice si la care forta seismica este distribuita liniar pe inaltime, verificarea se va face numai la ultimul nivel, unde S_niv are valoarea maxima.

Calculul rezistentei de proiectare a peretilor de zidarie

1.Conditii generale de calcul

1.1.Modelul de calcul.

(1) Modelul de calcul pentru determinarea rezistentei de proiectare a peretilor (elementelor) de zidarie trebuie sa tina seama de:

geometria peretelui;

conditiile de rezemare pe contur ale peretelui;

conditiile particulare de aplicare a incarcarilor;

proprietatile de rezistenta si de deformabilitate ale zidariei;

conditiile probabile de executie.

(2) Datele privind geometria peretelui se refera la:

• forma sectiunii transversale;
• raportul inaltime / grosime;
• existenta unor zone slabite (slituri, nise,etc).

(3) Conditiile de rezemare pe contur se refera la :

• modul de fixare la nivelul planseelor;
• modul de fixare laterala;
• efectele golurilor asupra conditiilor de rezemare.

(4) Conditiile particulare de aplicare a incarcarilor se refera la:

• excentricitatile de aplicare rezultate din alcatuirea constructiva;
• excentricitatile rezultate din imprecizia de executie (inclusiv din neuniformitatea proprietatilor materialelor);
• efectele incarcarilor de lunga durata.

(5) Proprietatile de rezistenta si deformabilitate se refera la:

• legea constitutiva a zidariei s-e;
• proprietatile reologice ale zidariei;
• compatibilitatea deformatiilor specifice ultime ale zidariei si betonului (in cazul cladirilor din zidarie armata - ZC, ZC+AR, ZIA).

(6) Rezistenta de proiectare a peretilor structurali se determina pentru:

a.)    solicitarile sectionale datorate sistemelor de forte care actioneaza in planul median al peretelui:

forta axiala (N_Rd);

moment incovoietor (M_Rd);

forta taietoare (V_Rd);

forta de lunecare verticala in peretii cu sectiuni compuse (V_Lhd);

b.)    solicitarile sectionale datorate fortelor care actioneaza perpendicular pe planul median al peretelui:

moment incovoietor in plan paralel cu rosturilor orizontale (M_Rxd1);

moment incovoietor in plan perpendicular pe rosturile orizontale (M_Rxd2).

(7) Pentru calculul rezistentei de proiectare a peretilor structurali se vor folosi caracteristicile geometrice ale peretilor si rezistentele de proiectare ale materialelor stabilite conform paragrafelor urmatoare.

1.2. Ipoteze de calcul

(1) Rezistenta de proiectare a peretilor de zidarie se determina in raport cu starea limita ultima (ULS) si, in cazurile special mentionate in text, in raport cu starea limita de serviciu (SLS).

(2) In conditiile simplificatoare mentionate la 1.1 2), determinarea eforturilor si deformatiilor din elementele de zidarie, se face pe baza urmatoarelor ipoteze:

ipoteza sectiunilor plane;

rezistenta la intindere a zidariei pe directie perpendiculara pe rostul orizontal este nula;

relatia efort unitar - deformatie specifica este dreptunghiulara pentru calculul la starea limita ultima (ULS);

relatia efort unitar deformatie specifica este triunghiulara pentru calculul la starea limita de serviciu (SLS).

NOTA Ipoteza de la (2) privind relatia efort unitar-deformatie specifica de forma dreptunghiulara se aplica numai daca legea constitutiva a zidariei s e are forma din figura 4.3. Pentru zidariile care au o alta forma a relatiei s e se aplica prevederile de la 4.1.2.1.(4).

1.3.Caracteristici geometrice ale sectiunii orizontale a peretelui

(1) Dimensiunile sectiunii transversale a peretilor de zidarie, folosite pentru calcul, sunt dimensiunile 'nete' (perete netencuit) care satisfac:

• conditiile minime de lungime de la 5.2.5.(6);
• conditiile minime de grosime de la 5.2.6 (2) si (3);
• conditiile maxime de lungime a talpilor active de la 3.1.(3).

(2) Peretii cu goluri cu dimensiunea maxima 0.2 l_w pot fi considerati in calcul ca pereti plini, daca golul este situat in treimea mijlocie a inaltimii nivelului iar plinurile de zidarie pana la marginile peretelui sunt cu cel putin 20% mai mari decat valorile minime date la 5.2.5 6)

(3) Golurile din talpi cu dimensiunea maxima h/4 pot fi neglijate iar golurile cu dimensiune > h/4 vor fi considerate margini ale talpii.

1.4. Rezistente unitare de proiectare ale zidariei, betonului si armaturii.

(1) Valorile rezistentelor unitare de proiectare ale zidariei, pentru calculul la starea limita ultima (ULS) se vor determina conform Cap.4 din prezentul Cod.

(2) Valorile rezistentelor unitare de proiectare ale zidariei, pentru calculul la starea limita de serviciu (SLS) se vor determina cu relatia (4.2), folosind:

i. Valoarea coeficientului partial de siguranta:

g_M = 1,50 pentru peretii structurali si nestructurali ai constructiilor din clasa de importanta I, definita conform Codului P100-1/2006;

g_M = 1 pentru toate celelalte elemente structurale si nestructurale, indiferent de clasa de importanta a constructiei.

ii. Valorile coeficientilor conditiilor de lucru m_z,SLS, conform 4.1.1.1.3.

(3) Valorile rezistentelor de proiectare pentru beton si armatura se vor lua din documentul de referinta STAS 10107/0-90.

2. Rezistenta de proiectare a peretilor la forta axiala

(1) Grosimea peretilor structurali pentru care se aplica prevederile acestui capitol, trebuie sa satisfaca, in afara conditiilor minime stabilite la 5.2. (2) si (3), si urmatoarele cerinte:

pentru pereti din zidarie armata (ZC, ZC+AR, ZIA): coeficientul de zveltete h_ef/t 20;

pentru pereti din zidarie nearmata (ZNA): coeficientul de zveltete h_ef/t 16;

unde h_ef este inaltimea efectiva a peretelui stabilita conform 2.1.3.

(2) Pentru peretii din zidarie, nearmata sau armata, solicitati la compresiune axiala, deformatia specifica maxima in zidarie (scurtare) se va lua ε_max = -2.

2.1. Rezistenta la compresiune a peretilor din zidarie nearmata (ZNA) cu

elemente din argila arsa

(1) Rezistenta de proiectare la compresiune centrica pentru un element din ZNA cu sectiune oarecare, se va determina cu relatia

N_Rd = F_{i (m)}Af_d (9)

unde:

F_i(m) - coeficientul de reducere a rezistentei datorita efectului zveltetei elementului si efectului excentricitatilor de aplicare a incarcarilor in sectiunile extreme (F_i) si, respectiv, in sectiunea de la ⅔ din inaltimea elementului masurata de la baza (F_m);

A - aria sectiunii transversale a elementului;

f_d - rezistenta de proiectare la compresiune a zidariei.

(2) In cazul peretilor de zidarie cu sectiune dreptunghiulara, rezistenta de proiectare la compresiune centrica se calculeaza, de regula, pentru unitatea de lungime a peretelui. Ecuatia (9) devine:

N_Rd(l) = F_i(m)tf_d (9a)

unde:

t grosimea peretelui;

N_Rd(l) - rezistenta de proiectare a peretelui dreptunghiular pe unitatea de

lungime.

2.1.1. Determinarea coeficientului de reducere a rezistentei F_i

Coeficientul de reducere a rezistentei in sectiunile de la extremitatile peretelui (F_i) - sus si jos - depinde numai de excentricitatea de aplicare a incarcarilor si se va determina cu relatia:

    (10)

unde

• t grosimea peretelui;
• e_i - excentricitatea de calcul, in raport cu planul peretelui, in sectiunea de la extremitatea peretelui (sus/jos) in care se face verificarea, calculata cu relatia:

(11)

cu notatiile:

• e_i0 - excentricitatea datorata tuturor incarcarilor aplicate peste nivelul de calcul determinata cu relatia (1);
• e_hi - excentricitatea datorata fortelor aplicate perpendicular pe planul peretelui determinata cu relatia (3);

• e_a - excentricitatea accidentala definita la 2.1.2.2

2.1.2.Determinarea coeficientului de reducere a rezistentei F_m

Pentru zidariile executate cu elemente din argila arsa, cu mortar pentru utilizare generala (G), cu toate rosturile complet umplute, coeficientul de reducere a rezistentei F_m va fi luat din tabelul 1, in functie de rapoartele h_ef/t si e_mk/t in care e_mk este excentricitatea de calcul in zona centrala a peretelui (la ⅔ h_et, masurata de la baza peretelui) calculata cu relatia:

e_mk = e_m + e_k (12)

in care

(13)

si

(14)

unde

• h_ef - inaltimea efectiva a peretelui calculata conform 2.1.3.;

• e_i0 - excentricitatea in sectiunea de sus a peretelui calculata cu relatia (1);
• e_hm - excentricitatea datorata efectului incarcarilor orizontale, in

sectiunea de la ⅔ din inaltimea peretelui, calculata cu relatia (3);

• e_a - excentricitatea accidentala determinata conform 2.1.2.2.;
• e_k - excentricitatea datorata curgerii lente;
• F - coeficientul de curgere lenta dat in tabelul 4.10.

Valorile coeficientului F_m Tabelul 1

NOTE 1^o. Tabelul 1 este preluat din documentul normativ de referinta EN 1996-1-1 si este calculat cu modulul de elasticitate al zidariei E_z = 1000 f_k. Pentru alte valori ale modulului de elasticitate, calculul coeficientului F_m se poate face cu relatiile din anexa E (informativa) la documentul de referinta EN 1996-1-1 .

2^o Pentru valori intermediare ale rapoartelor h_ef/t si e_mk/t valorile F se pot obtine prin interpolare. Nu este permisa extrapolarea valorilor din tabel

3^o. Excentricitatea e_k poate fi neglijata in cazul zidariilor cu elemente din argila arsa.

2.1.3. Determinarea inaltimii efective a peretelui (h_ef)

(1) Inaltimea efectiva a unui perete de zidarie (h_ef) se stabileste in functie de dimensiunile panoului (h, l_w) si de conditiile de legatura ale acestuia cu elementele adiacente (plansee si/sau pereti perpendiculari).

(2) Pentru a fi considerate reazeme laterale, elementele care marginesc peretele trebuie sa aiba rigiditate comparabila cu cea a peretelui pe care il rigidizeaza.

(3) Un perete din zidarie poate fi considerat rigidizat daca este legat, prin tesere, cu un perete din zidarie perpendicular care indeplineste urmatoarele conditii:

• lungimea peretelui de rigidizare este 1/5 din inaltimea etajului;
• grosimea peretelui de rigidizare este din grosimea peretelui care este rigidizat;
• in cazul in care peretele de rigidizare are goluri in vecinatatea peretelui rigidizat, lungimea acestuia trebuie sa indeplineasca conditiile din figura 9.

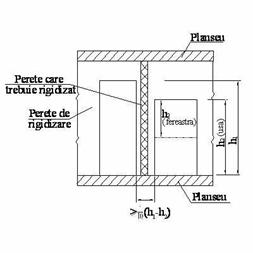
Figura 9

Rigidizarea unui perete cu pereti transversali

NOTA. In cazul peretilor cu grosimea de 240 mm, peretii de rigidizare de caramida (120 mm) sunt luati in considerare numai ca element de rigidizare pentru stabilirea inaltimii efective a peretelui si nu sunt considerati pereti activi pentru preluarea fortelor seismice.

(4) Rigidizarea unui perete poate fi asigurata si prin executarea unor stalpi de zidarie (pilastri) cu grosimea t_pilastru 3t dispusi la distante interax d_pilastru 20 t unde t este grosimea peretelui care se rigidizeaza. Zidaria peretelui va fi tesuta cu cea a pilastrului.

(5) Pentru calculul capacitatii de rezistenta, grosimea reala a peretelui rigidizat cu pilastri de zidarie (t), se multiplica cu coeficientul supraunitar r_w din tabelul 2.

t_calc = r_wt (15)

Coeficientul de majorare a grosimii peretelui rigidizat cu pilastri

Tabelul 2

NOTA. Pentru situatiile intermediare se poate interpola intre valorile din tabel.

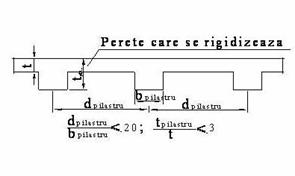
Figura 10

Rigidizarea peretilor cu pilastri din zidarie

(6) Inaltimea efectiva (h_ef) a unui perete de zidarie va fi calculata cu relatia :

h_ef = r_n h (16)

unde

• r_n (n = 2 4) - coeficient care tine seama de conditiile de rezemare pe contur si

de numarul laturilor peretelui care sunt rezemate/rigidizate;

• h - inaltimea libera a peretelui;
• l_w - lungimea sectiunii orizontale a peretelui.

(7) Coeficientii r_n se stabilesc dupa cum urmeaza:

i₁ . Perete fixat cu planseu de beton armat sau din lemn dispus pe ambele parti:

r₂ = 0.75

i₂ . Perete fixat cu planseu de beton armat sau din lemn dispus pe o singura

parte (perete exterior , de exemplu):

r₂ = 1.00

In functie de conditiile de fixare la nivelul planseelor (r₂) coeficientii r₃ (pentru perete rigidizat pe o latura verticala) si r₄ (pentru perete rigidizat pe doua laturi verticale) se determina conform tabelul 3.

Tabelul 3

2.2. Rezistenta la compresiune a peretilor din zidarie armata ZC, ZC+AR,ZIA

(1) Rezistenta peretilor din zidarie armata se va calcula prin transformarea sectiunii mixte intr-o sectiune ideala de zidarie folosind coeficientul de echivalenta dat de relatia ( ). Calculul se va conduce apoi ca la

(2) Contributia armaturilor din stalpisori (ZC, ZC+AR) si din stratul median (ZIA) la preluarea fortei de compresiune se va neglija.

2.3. Rezistenta peretilor la compresiune locala sub efectul incarcarilor concentrate

(1) Pentru un perete din ZNA, alcatuit cu elemente de zidarie din grupa 1, rezistenta de proiectare la compresiune locala datorita incarcarilor concentrate se va determina cu relatia:

N_Rd,cl = bA_bf_d (17)

unde: (18)

cu notatiile:

• b - coeficient de majorare pentru incarcari concentrate;

• a₁ - distanta de la capatul peretelui pana la cea mai apropiata margine a ariei pe

care se transmite incarcarea;

• A_b - aria pe care se aplica incarcarea 0.45 A_ef;

• H_o - inaltimea peretelui de la baza pana la nivelul la care se aplica incarcarea

concentrata;

• A_ef - aria incarcata;
• A_ef = t L_ef unde este lungimea efectiva de preluare a incarcarii masurata la jumatatea inaltimii peretelui sau pilastrului rezultata prin descarcarea fortei verticale la un unghi de 60^o cu orizontala (vezi figura 2a).

Valorile din relatia (18) se limiteaza dupa cum urmeaza:

b_max = 1.25 daca

b_max = 1.50 daca

Pentru valorile se vor obtine prin interpolare liniara intre valorile b_max date mai sus.

(2) Excentricitatea de aplicare a fortei concentrate, fata de planul median al peretelui, nu va depasi din grosimea t a peretelui.

(3) In cazurile in care efectele fortelor concentrate se suprapun, sectiunea de la mijlocul inaltimii peretelui va fi verificata cu relatia (17).

(4) Forta concentrata trebuie sa fie aplicata pe o zidarie cu elemente de grupa 1 sau, in cazul zidariilor cu elemente din grupele 2 si 2S, prin intermediul unui material rigid care sa permita distributia pe verticala a incarcarii la un unghi de 30^o cu verticala asigurand realizarea unei lungimi de incarcare L_ef ca in figura 2a(1) (in cazul reazemelor situate la capatul peretelui, descarcarea la 30^o se va considera numai pe o singura parte a incarcarii). figura 2a(2).

(5) In cazul in care forta concentrata este aplicata prin intermediul unui cuzinet cu rigiditate satisfacatoare efortul de compresiune sub forta concentrata (s_cl) nu trebuie sa depaseasca 1.5 f_d in cazul elementelor de zidarie din grupele 1 si 2 si f_d in cazul elementelor de zidarie din grupa 2S.

NOTA. Se poate considera ca un cuzinet cu latimea egala cu grosimea peretelui, cu inaltimea de 200 mm si cu lungimea de trei ori mai mare decat lungimea pe care este rezemata incarcarea are rigiditatea necesara pentru a satisface aceste conditii.

3. Rezistenta de proiectare la forta axiala si incovoiere in planul median a

peretilor din zidarie

3.1.Conditii generale de calcul

(1) Ipotezele generale de calcul folosite pentru determinarea rezistentei de proiectare la forta axiala si moment incovoietor in planul peretelui pentru zidarii nearmate si armate sunt urmatoarele:

• ipoteza sectiunilor plane;
• in cazul sectiunilor din zidarie armata (ZC si ZIA) betonul conlucreaza cu zidaria pana in stadiul ultim; deformatiile ultime ale betonului (e_ub) luate in calcul nu pot insa depasi valorile deformatiilor specifice ultime ale zidariei (e_uz) care sunt date in 4.1.2.1.(3);
• rezistenta la intindere a zidariei se neglijeaza;
• in stadiul ultim, eforturile unitare in zona comprimata a zidariei se considera uniform distribuite; idem pentru beton;
• relatia efort unitar‑deformatie specifica pentru armaturi se va lua din documentul normativ de referinta STAS 10107/0-90;2

NOTA Ipoteza referitoare la distributia uniforma a eforturilor unitare in zidarie este valabila numai daca legea constitutiva a zidariei are forma din figura 4.3. Pentru zidariile care au o alta forma a relatiei s e se aplica prevederile de la 4.1.2.1.(4).

(2) In cazul peretilor cu forma complexa a sectiunii transversale (I, L,T) rezistenta de proiectare la forta axiala si moment incovoietor in planul peretelui se va determina pe baza sectiunii de calcul cu lungimile talpilor determinate la art.3.1.(3); se va verifica, daca talpa comprimata satisface conditia de rezistenta la compresiune data la 2.1.

(3) Legaturile dintre inima si talpile peretilor cu forma complexa precum si sectiunile slabite prin slituri verticale (a se vedea 7.1.1.2) vor fi verificate pentru eforturile de lunecare verticale conform prevederilor de la 8.1.1 2).

(4) Verificarea de la (3) nu este necesara daca legatura intre talpa si inima peretelui satisface conditiile de mai jos:

i) Pentru zidaria nearmata (ZNA) :

zidurile de pe cele doua directii sunt executate simultan (complet tesute);

sectiunea de legatura intre pereti nu este slabita prin slituri verticale;

la colturi, intersectii si ramificatii sunt prevazute in rosturile orizontale armaturile minime stabilite in Codul P 100-1/200si in prezentul Cod

ii) Pentru zidaria confinata, cu sau fara armaturi in rosturile orizontale (ZC/ZC+AR):

strepii reprezinta 50% din suprafata de contact intre zidarie si beton;

sectiunea de legatura intre pereti nu este slabita prin slituri verticale;

la colturi, intersectii si ramificatii sunt prevazute in rosturile orizontale armaturile minime stabilite in Codul P 100-1/2006 si in prezentul Cod.

(5) Daca la legatura intre inima si talpa sau pe lungimea talpii active se afla slituri cu adancime mai mare decat valoarea limita data la 7.1.1.1., sectiunea respectiva se considera margine libera.

3.2. Pereti din zidarie nearmata

(1) Rezistenta de proiectare la incovoiere (M_Rd), asociata fortei axiale de proiectare (N_Sd), pentru incarcari neseismice (gravitationale) aplicate in planul median al unui perete, se va calcula pe baza ipotezelor de la 3.1. considerand ca blocul eforturilor de compresiune are forma dreptunghiulara cu valoare 0.8f_d.

(2) In conditiile de la (1), rezistenta de proiectare la incovoiere (M_Rd) se va calcula dupa cum urmeaza:

Se determina aria zonei comprimate a peretelui

(19)

Se determina distanta y_zc de la centrul de greutate al peretelui pana la centrul de greutate al zonei comprimate.

Se determina rezistenta de proiectare la incovoiere (M_Rd) cu relatia

(20)

(3) In cazul particular al unui perete dreptunghiular, cu lungime l_w si grosime t relatiile (19) si (20) devin:

• adancimea zonei comprimate (19a)
• momentul incovoietor de proiectare (20a)

(4) In cazul in care forta axiala este aplicata excentric fata de planul peretelui, adancimea zonei comprimate se va determina cu relatia:

(21)

unde coeficientul F_i(m) se va determina conform prevederilor de la 2.1.1 si 2.1.2.

(5) In cazul peretilor din zidarie nearmata la care incovoierea in planul peretelui este produsa de forta seismica, rezistenta de proiectare la incovoiere (M_Rd) asociata fortei axiale de proiectare (N_Ed) se va determina ca si pentru incarcarile neseismice, dar cu limitarea ariei pe care se dezvolta eforturi de intindere prin conditia

y_zc < 1.2 r_sc    (22)

unde

r_zc - distanta de la centrul de greutate al sectiunii orizontale a peretelui pana la limita samburelui central aflata de aceasi parte cu fibra comprimata.

NOTA Forta axiala de proiectare N_Ed se determina din gruparea de incarcari care include actiunea seismica, conform prevederilor Codului P 100-1/200

(6) In cazul particular al unui perete dreptunghiular cu lungime l_w, din conditia ( 22 ) relatia (20a) devine

M_Rd = 0.2 l_wN_Ed (20b)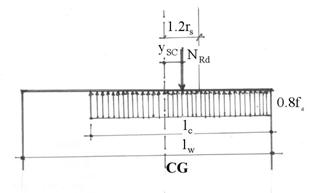

Figura 11

Calculul rezistentei de proiectare la incovoiere cu forta axiala pentru zidaria nearmata

3.3. Pereti din zidarie confinata cu sau fara armaturi in rosturile orizontale

(1) Calculul rezistentei de proiectare la incovoiere (M_Rd) asociata fortei axiale de proiectare din incarcari seismice (N_Ed) pentru peretii de zidarie confinata (ZC, ZC+AR), executati cu elemente de zidarie din grupele 1, 2 si 2S, se face in urmatoarele ipoteze:

se neglijeaza:

rezistenta la eforturi unitare de intindere a betonului din stalpisorul de la extremitatea solicitata la intindere a peretelui (pentru ipoteza respectiva de incarcare);

rezistenta mortarului din rosturile orizontale ale zidariei;

sectiunea de beton si armatura eventualilor stalpisori intermediari;

se tine seama de aportul elementelor de confinare verticale:

sectiunea de beton a stalpisorului de la extremitatea comprimata;

armatura ambilor stalpisori de la extremitati.

in stadiul ultim, starea de deformatie, in situatia de 'balans', este urmatoarea:

la extremitatea comprimata se ating valorile maxime ale deformatiilor

specifice ale zidariei/ betonului date la 3.1.(1).

in armatura stalpisorului de la extremitatea intinsa se atinge rezistenta de curgere a otelului.

blocul eforturilor de compresiune in zidarie si/sau beton este dreptunghiular si se dezvolta pe o adancime de 0.80 x unde 'x' este distanta de la axa neutra pana la fibra cea mai comprimata .

Nota. Ipoteza referitoare la distributia uniforma a eforturilor unitare in zidarie este valabila numai daca legea constitutiva a zidariei are forma din figura 4.3. Pentru zidariile care au o alta forma a relatiei s e se aplica prevederile de la 4.1.2.1.(4).

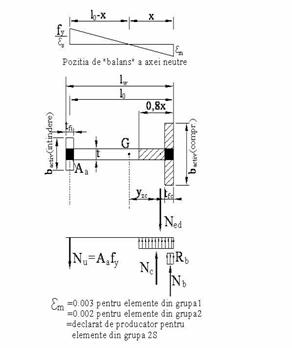
Figura 12

Calculul rezistentei de proiectare la incovoiere cu forta axiala pentru zidaria confinata

(2) In cazul folosirii elementelor din grupele 2 si 2S, pentru care e_uz < e_ub se va proceda dupa cum urmeaza:

pentru extremitatile fara talpi ale peretelui, deformatia specifica a zidariei, la limita cu stalpisorul de beton, nu va fi mai mare decat deformatia specifica maxima conform 3.1., iar deformatia specifica maxima in betonul stalpisorului, rezultata din ipoteza sectiunilor plane, nu va depasi e_c = - 3.0

pentru extremitatile la care exista talpa, deformatia specifica maxima a betonului din stalpisor (e_ub) nu va fi mai mare decat deformatia specifica maxima a zidariei data la 3.1.

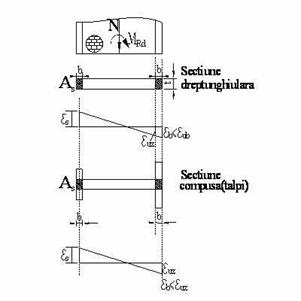
Figura 13

Deformatii specifice ultime la pereti din zidarie confinata

(3) Pentru a se asigura atingerea stadiului ultim prin curgerea otelului inaintea ruperii fragile prin zdrobirea zidariei din zona comprimata, aria armaturii din stalpisori se va lua egala cu cel mult 50% din armatura care realizeaza simultan atingerea deformatiilor ultime in otelul intins si in zidaria comprimata (armatura de 'balans');

(4) Daca nu este necesar un calcul mai exact, rezistenta de proiectare la incovoiere (M_Rd), asociata fortei axiale de proiectare (N_Ed), pentru un perete de zidarie confinata de forma oarecare, poate fi calculata prin insumarea rezistentei de proiectare la incovoiere a sectiunii ideale de zidarie nearmata M_Rd (zna,i) cu rezistenta de proiectare la incovoiere corespunzatoare armaturilor din stalpisorii de la extremitati M_Rd(A_s) calculate conform aliniatelor (5) (7).

M_Rd = M_Rd(zna,i) + M_Rd (A_s)    (23)

(5) Rezistenta de proiectare la incovoiere a sectiunii ideale de zidarie nearmata se calculeaza in urmatoarele ipoteze:

este valabila ipoteza sectiunilor plane;

aria de beton armat a stalpisorilor comprimati poate fi inlocuita cu o arie echivalenta de zidarie; coeficientul de echivalenta n_ech se ia egal cu raportul dintre valoarea de baza a rezistentei de proiectare la compresiune a betonului din stalpisor (f_cd*) redusa cu coeficientul conditiilor de lucru m = 0.75 si rezistenta de proiectare la compresiune a zidariei (f_d):

(24)

blocul eforturilor de compresiune are forma dreptunghiulara, cu valoarea maxima egala cu 0.80 f_d;

adancimea maxima a zonei comprimate va fi x x_max = 0,30 l_w unde l_w este lungimea peretelui.

NOTE. 1^o. Ipoteza referitoare la distributia uniforma a eforturilor unitare in zidarie este valabila numai daca legea constitutiva a zidariei are forma din figura 4.3. Pentru zidariile care au o alta forma a relatiei s e se aplica prevederile de la 4.1.2.1.(4).

2⁰ Pentru zidariile la care e_uz 2 coeficientul de echivalenta se va determina tinand seama de valoarea efortului din beton corespunzatoare deformatiei efective rezultata din conditiile de la (2) si din ipoteza sectiunilor plane (in multe cazuri aceasta valoare poate fi mai mica decat f_cd^*)

(6) Cu ipotezele de la (5) rezulta:

aria sectiunii ideale de zidarie comprimata (A_zci

• momentul incovoietor de proiectare al sectiunii ideale de zidarie

(26)

unde

• y_zci - distanta de la centrul de greutate al peretelui pana la centrul de greutate al zonei comprimate a sectiunii ideale de zidarie

(7) Rezistenta de proiectare la incovoiere data de armaturile stalpisorilor M_Rd(A_s) se calculeaza cu relatia

(27)

unde

l_s - distanta intre centrele de greutate ale celor doi stalpisori de la extremitati;

A_s cea mai mica dintre ariile de armare ale celor doi stalpisori;

f_yd rezistenta de calcul a armaturii din stalpisori.

3.4. Pereti de zidarie cu inima armata

(1) Rezistenta de proiectare la incovoiere (M_Rd) asociata fortei axiale de proiectare (N_Ed), pentru zidaria cu inima armata (ZIA) se va calcula folosind urmatoarele ipoteze:

ipoteza sectiunilor plane;

zidaria, betonul si armatura au comportare ductila definita de curbele 's-e' respective;

straturile paralele de zidarie si beton conlucreaza pana in stadiul ultim;

blocul eforturilor de compresiune in stadiul ultim este dreptunghiular cu

adancimea x_conv = 0.80x unde x este distanta de la fibra cea mai comprimata

pana la axa neutra a sectiunii orizontale a peretelui;

deformatiile specifice in stadiul ultim ale zidariei si betonului sunt egale

e_ub e_uz daca se folosesc elemente de zidarie din grupa 1; in cazul

zidariei cu elemente din grupele 2 si 2S deformatia ultima a betonului va fi

luata egala cu deformatia ultima a zidariei, respectiv e_uz pentru

elemente din grupa 2 sau valoarea declarata de catre producator pentru

elemente din grupa 2S;

armatura stratului median este uniform distribuita in lungul peretelui (a_s in mm²/m).

NOTA. Ipoteza referitoare la distributia uniforma a eforturilor unitare in zidarie este valabila numai daca legea constitutiva a zidariei are forma din figura 4.3. Pentru zidariile care au o alta forma a relatiei s e se aplica prevederile de la 4.1.2.1.(4).

(2) In ipotezele mentionate la (1) rezistenta de proiectare la incovoiere (M_Rd) asociata fortei axiale de proiectare (N_Ed) se poate calcula, suficient de precis, prin insumarea rezistentei de proiectare la incovoiere a sectiunii ideale de zidarie nearmata cu rezistenta de proiectare a armaturilor din stratul median

M_Rd (ZIA) = M_Rd (zna,i) + M_Rd (a_s) (28)

(3) Grosimea echivalenta a sectiunii ideale de zidarie nearmata se va calcula cu relatia:

t_ech = 2t_z +n_echt_m (29)

unde:

t_z grosimea straturilor de zidarie exterioare;

t_m grosimea stratului median de mortar/beton (grout);

• n_ech coeficientul de echivalenta calculat cu relatia (24)

(4) Rezistenta de proiectare a sectiunii ideale de zidarie nearmata M_Rd (zna,i) se va calcula conform art.

(5) Rezistenta de proiectare a armaturilor, M_Rd (a_s), se va calcula cu relatia:

(30)

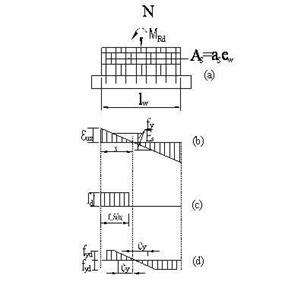
Figura 14

Rezistenta de proiectare la incovoiere cu forta axiala pentru zidaria cu inima armata

4. Rezistenta de proiectare la forta taietoare a peretilor structurali de

zidarie

4.1. Ipoteze de calcul

(1) Rezistenta de proiectare la forta taietoare a peretilor dreptunghiulari de zidarie se determina considerand ca eforturile unitare tangentiale date de forta taietoare de proiectare sunt uniform distribuite pe lungimea zonei comprimate a peretelui. Lungimea zonei comprimate rezulta din solicitarile sectionale de proiectare (moment incovoietor si forta axiala) provenite din gruparea respectiva de incarcari si se determina conform metodologiei de la 3.

(2) In cazul peretilor in forma de I,L,T rezistenta de proiectare la forta taietoare a peretelui este egala cu rezistenta de proiectare la forta taietoare a inimii (sectiunea dreptunghiulara).

4.2. Pereti de zidarie nearmata

(1) Rezistenta de proiectare la forta taietoare V_Rd a peretilor de zidarie nearmata, se va calcula cu relatia

V_Rd = f_vdtl_c (31)

unde

• f_vd - rezistenta unitara de proiectare la forfecare a zidariei, stabilita cu relatia (4.4) ;
• t - grosimea inimii peretelui;
• l_c - lungimea zonei comprimate a inimii peretelui.

(2) Efortul unitar de compresiune (s_d) folosit pentru determinarea rezistentei unitare de proiectare (f_vd) in relatia (31), se va calcula considerand ca incarcarea verticala de proiectare din gruparea respectiva de incarcari, N_Sd sau N_Ed, este uniform distribuita pe zona comprimata a peretelui determinata conform 3.2. In cazul peretilor cu sectiune compusa (L,T,I), in zona comprimata pentru care se determina s_d se includ si talpile cu dimensiunile stabilite la 3.1.(3).

NOTA. In cazul solicitarii seismice, aria zonei comprimate se va determina avand in vedere limitarea excentricitatii fortei axiale din relatia (22).

(3) Armatura constructiva dispusa in centurile planseelor conform prevederilor al.7.1.2.1 5) nu va fi luata in considerare pentru calculul rezistentei la forta taietoare.

4.3. Pereti de zidarie confinata

(1) Rezistenta de proiectare la forta taietoare a peretilor de zidarie confinata, V_Rd, se obtine prin insumarea de rezistentei de proiectare la forta taietoare a panoului de zidarie nearmata (V_Rd1) si a rezistentei de proiectare la forfecare datorata armaturii din stalpisorul de la extremitatea comprimata a peretelui (V_Rd2).

V_Rd = V_Rd1 + V_Rd2 (32)

(2) Rezistenta de proiectare la forta taietoare a panoului de zidarie nearmata (V_Rd1) se va calcula conform 4.2. cu relatia (31) in care se va introduce lungimea zonei comprimate l_c determinata conform 3.3.

(3) In cazul fortei taietoare provenita din actiunea seismica, valoarea rezistentei de proiectare a panoului de zidarie nearmata (V_Rd1), determinata cu relatia (31) va fi redusa prin inmultire cu un coeficient subunitar stabilit prin Codul P 100-1/200

(4) Rezistenta de proiectare la forfecare a armaturii verticale din stalpisorul comprimat se va calcula cu relatia:

V_Rd2 = 0.2 A_ascf_yd (33)

unde

• A_asc - aria armaturii din stalpisorul de la extremitatea comprimata;
• f_yd - rezistenta de proiectare a armaturii din stalpisorul comprimat.

(5) O parte, cel mult 50%, din armatura din centura planseului superior, prevazuta conform 7.1.2.2.2 5), poate fi considerata ca armatura in rosturile orizontale a carei contributie se calculeaza conform pct. 4.4.

4.4. Pereti de zidarie confinata si armata in rosturile orizontale (ZC+AR)

(1) Rezistenta de proiectare la forta taietoare a peretilor de zidarie confinata si armata in rosturile orizontale se calculeaza prin insumarea rezistentei la forta taietoare a zidariei confinate (V_Rd1+V_Rd2 - determinata cu relatiile de la 4.3.) si a rezistentei de proiectare a armaturilor din rosturile orizontale (V_Rd3).

V_Rd = V_Rd1 + V_Rd2 + V_Rd3 (34)

(2) Rezistenta de proiectare a armaturilor din rosturile orizontale (V_Rd3) se calculeaza, in cazul peretilor cu inaltimea totala (h_tot) lungimea peretelui (l_w) cu relatia:

(35)

unde

• l_w - lungimea peretelui;
• A_sw - aria armaturilor din rostul orizontal (pentru preluarea fortei taietoare);
• s - distanta pe verticala intre doua randuri succesive de armaturi A_sw;
• f_ysd - rezistenta de proiectare a armaturii din rosturile orizontale.

In cazul peretilor cu inaltimea totala (h_tot) < lungimea peretelui (l_w) in relatia (35) se va inlocui l_w cu h_tot

(3) O parte, cel mult 50%, din armatura din centurile planseelor poate fi adaugata armaturii din rosturile orizontale intersectata de o fisura la 45^o(SA_sw).

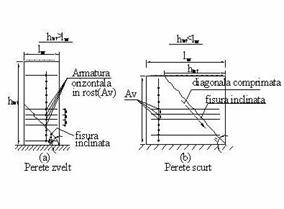
Figura 15

Rezistenta de proiectare a armaturilor din rosturile orizontale ale zidariei

4.5. Pereti de zidarie cu inima armata

(1) Rezistenta de proiectare la forta taietoare a peretilor din zidarie cu inima armata

- V_Rd (ZIA) se determina prin insumarea rezistentelor de proiectare la forta taietoare ale celor trei materiale componente:

V_Rd (ZIA) = V_Rdz + V_Rdb + V_Rda (36)

unde

• V_Rdz    rezistenta de proiectare la forta taietoare a zidariei;
• V_Rdb    rezistenta de proiectare la forta taietoare a stratului median de beton

sau mortar-beton;

• V_Rda    rezistenta de proiectare la forta taietoare a armaturilor orizontale din

stratul median.

(2) Lungimea zonei comprimate a peretelui din zidarie cu inima armata si valoarea efortului unitar de compresiune in perete se determina pe baza ipotezelor de la 4.4.

(3) Rezistenta de proiectare la forta taietoare a zidariei V_Rdz se determina cu relatia

V_Rdz = f_vd l_c t_z (37)

in care

f_vd rezistenta de proiectare la forfecare a zidariei;

l_c lungimea zonei comprimate a peretelui;

t_z grosimea totala a celor doua straturi de zidarie.

(4) In cazul in care forta taietoare provine din actiunea cutremurului, rezistenta de proiectare la forfecare a zidariei se va reduce prin inmultire cu un coeficient subunitar conform prevederilor Codului P 100-1/2006 .

(5) Rezistentele de proiectare la forta taietoare ale stratului de beton (V_Rdb) si ale armaturilor orizontale (V_Rda) se vor calcula conform prevederilor Codului de proiectare CR.2-1-1.1.

4. Rezistenta de proiectare la forta de lunecare verticala

asociata incovoierii peretelui

Rezistenta de proiectare la forta de lunecare verticala la legatura intre inima si talpa unui perete cu sectiune compusa (I,L,T) si in sectiunile slabite de slituri verticale se calculeaza pe inaltimea unui etaj admitand ca eforturile unitare de forfecare sunt uniform distribuite pe inaltimea etajului, cu relatia:

(38)

unde

V_Lhd rezistenta de proiectare la lunecare pe inaltimea etajului;

h_et inaltimea etajului;

t_L grosimea peretelui in sectiunea in care se calculeaza rezistenta peretelui;

f_vk0 rezistenta caracteristica la forfecare a zidariei sub efort de compresiune

egal cu zero;

g_M coeficientul de siguranta conform 2.3.2.3.

5. Rezistenta de proiectare a panourilor de zidarie de umplutura

(1) Rezistenta de proiectare a panourilor de zidarie de umplutura F_Rd (zu) va fi luata egala cu cea mai mica dintre valorile corespunzatoare urmatoarelor moduri de rupere ale zidariei:

rupere prin lunecare din forta taietoare in rosturile orizontale (de regula, la jumatatea inaltimii panoului) - F_Rd1(zu) figura 16 Rd1;

strivirea diagonalei comprimate la coltul cadrului - F_Rd2 (zu) figura 16 Rd2;

fisurarea diagonala in lungul bielei comprimate - F_Rd3 (zu) figura 16 Rd3;

F_Rd (zu) = min (F_Rd1,F_Rd2,F_Rd3)    (39)

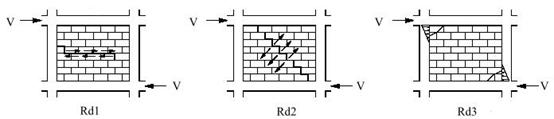
Figura 16

Rezistenta de proiectare a panourilor de zidarie de umplutura

(2) Rezistenta de proiectare corespunzatoare mecanismului de rupere prin lunecare din forta taietoare in rosturile orizontale se determina cu relatia:

unde

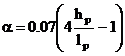(41)

(3) Rezistenta de proiectare corespunzatoare mecanismului de rupere prin strivirea diagonalei comprimate se determina cu relatia:

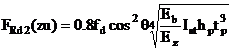(42)

(4) Rezistenta de proiectare corespunzatoare mecanismului de rupere prin fisurarea diagonala in lungul diagonalei comprimate se determina cu relatia:

(5) In relatiile (40) (43) s-au folosit notatiile:

h_p inaltimea panoului de zidarie;

l_p lungimea panoului de zidarie;

t_p grosimea panoului de zidarie;

q unghiul cu orizontala al diagonalei panoului de zidarie;

• E_b, E_z modulii de elasticitate al betonului din cadru si al zidariei (valorile de

scurta durata);

• I_st    valoarea medie a momentelor de inertie ale stalpilor care marginesc

panoul;

• f_d    rezistenta de proiectare la compresiune a zidariei;
• f_vd0    rezistenta de proiectare la forfecare sub efort de compresiune zero a

zidariei.

Rezistenta de proiectare a peretilor supusi la incovoiere perpendicular pe

planul median

(1) Pentru calculul rezistentelor de proiectare la incovoiere perpendicular pe planul peretelui de zidarie (M_Rxd1 si M_Rxd2) se vor folosi rezistentele de proiectare la intindere din incovoiere perpendicular pe planul zidariei, f_xd1, f_xd2, determinate cu relatiile (4.5a) si (4.5b).

(2) Pentru peretii de zidarie confinata si armata in rosturile orizontale, la calculul momentului M_Rxd2 (cu plan de rupere perpendicular pe rosturile orizontale) se va tine seama si de armaturile din rosturile orizontale care sunt ancorate corespunzator in stalpisorii care marginesc panoul.

(3) Valorile M_Rxd1 si M_Rxd2 (in Nmm) se calculeaza, pentru o banda din perete de latime egala cu 1000 mm, cu relatiile:

M_Rxd1 = W_w f_xd1 (44a)

M_Rxd2 = W_w f_xd2 (44b)

unde

modulul de rezistenta al peretelui (mm³) ;

t - grosimea peretelui in mm.

7. Calculul rezistentei de proiectare a planseelor

(1) Capacitatea de rezistenta a planseelor de beton armat la incarcari verticale se va stabili luand ca document normativ de referinta STAS 10107/0 4.

(2) Capacitatea de rezistenta a planseelor din lemn la incarcari verticale se va lua din documentele normative de referinta NP 019-1997 si NP 005-2003.

8. Verificarea sigurantei cladirilor din zidarie

(1) Verificarea sigurantei cladirilor de zidarie se va face prin calcul, cu exceptia 'Structurilor simple', proiectate conform prevederilor din Codul P 100-1/200

(2) Verificarea sigurantei cladirilor de zidarie se face in raport cu:

starile limita ultime de rezistenta si de stabilitate (ULS);

starea limita a exploatarii normale (SLS).

8.1. Verificarea cerintei de rezistenta

8.1.1. Verificarea cerintei de rezistenta pentru solicitarile in planul peretelui

(1) Elementele structurale si nestructurale de zidarie vor fi proiectate pentru a avea, in toate sectiunile, rezistentele de proiectare la eforturi sectionale (N_Rd, M_Rd, V_Rd) mai mari decat eforturile sectionale de proiectare (N_Sd, M_Sd, V_Sd) rezultate din incarcarile cele mai defavorabile din gruparile de incarcari, luand ca document normativ de referinta STAS 10101/OA-77.

(2) In cazul in care incarcarile cele mai defavorabile provin din grupari care includ actiunea seismica se va proceda dupa cum urmeaza:

• rezistentele de proiectare la eforturi sectionale (N_Rd, M_Rd, V_Rd) ale peretilor structurali vor fi stabilite conform 6, considerand suprarezistenta armaturilor in situatiile mentionate in Codul P100-1/2006;
• eforturile sectionale de proiectare vor avea valorile (N_Ed, M_Ed, V_Ed) care vor fi determinate conform prevederilor din Codul P 100-1/2006;
• in cazurile mentionate la 4. rezistenta de proiectare la lunecare verticala

(V_Lhd) va fi mai mare decat forta de lunecare verticala L_v,et calculata conform

3.2.2.; pentru calculul fortei de lunecare, in relatia (5) momentele

incovoietoare se vor introduce cu valorile de proiectare stabilite conform

Codului P 100-1/2006;

• verificarea cerintei de rezistenta se va face in conditiile stabilite prin Codul P 100-1/2006

(3) Peretii de zidarie de umplutura din structurile din cadre se vor verifica la starea limita ultima, separat, pentru:

efectele rezultate din interactiunea cu structura in cazul solicitarii seismice;

efectele actiunii seismice sau a presiunii vantului perpendiculara pe planul peretelui .

(4) Cerinta de siguranta pentru efectele rezultate din interactiunea peretilor de zidarie de umplutura cu cadrul este indeplinita daca este satisfacuta relatia:

F_Ed (zu) F_Rd (zu) (45)

unde

F_Ed (zu) -forta axiala de proiectare din diagonala comprimata corespunzatoare

actiunii seismice de proiectare;

F_Rd (zu) - rezistenta de proiectarea a panoului de umplutura determinata

conform 5.

(5) Stalpii si grinzile cadrului se vor verifica pentru fortele si deformatiile suplimentare rezultate din interactiunea cu panoul de zidarie luand valorile din documentul normativ de referinta STAS 10107/0-90. in cazul cadrelor din beton armat cele din documentul de referinta STAS 10108/0-78 in cazul cadrelor din otel.

8.1.2. Verificarea cerintei de rezistenta pentru solicitarile perpendiculare pe

planul peretelui

(1) Cerinta de rezistenta la actiunea fortelor perpendiculare pe plan, este indeplinita daca exista relatiile:

M_Rxd1 M_Sxd1 (46a)

M_Rxd2 M_Sxd2 (46b)

unde

• M_Sxd1 si M_Sxd2 sunt momentele incovoietoare de proiectare datorate fortelor perpendiculare pe plan stabilite conform 4.
• M_Rxd1 si M_Rxd2 sunt rezistentele pe proiectare la incovoiere perpendicular pe planul peretelui de zidarie determinate conform

(2) In cazul curent, cand incarcarea perpendiculara pe plan provine din actiunea seismica, momentele incovoietoare de proiectare vor avea valorile M_Exd1 si M_Exd2 determinate conform Codului P 100-1/2006;

(3) Panourile de zidarie pentru care nu sunt indeplinite conditiile (46a) si (46b) vor fi tratate conform prevederilor de la 7.3.1 3)

8.1.3. Verificarea cerintei de rezistenta pentru plansee

(1) Verificarea cerintei de rezistenta pentru incarcarile verticale se face conform reglementarilor specifice pentru fiecare material de constructie.

(2) Pentru incarcarile orizontale din cutremur, cerinta de rezistenta este satisfacuta daca, prin dimensionarea si alcatuirea constructiva, se asigura comportarea planseelor in domeniul elastic pentru solicitarile asociate capacitatilor de rezistenta ale peretilor structurali in stadiul ultim.

8.2. Verificarea cerintei de rigiditate

(1) Cerinta de rigiditate la actiunea fortelor seismice a cladirilor de zidarie este satisfacuta daca deplasarile relative de nivel ale cladirii d_r se inscriu in limitele stabilite in Codul P100-1/200

(2) Cerinta de rigiditate a planseelor implica:

• limitarea deformatiilor verticale la valorile stabilite prin reglementarile specifice in functie de:

materialul de constructie (beton armat sau lemn);

pozitia planseului in cladire (planseu curent, planseu de acoperis);

caracteristicile peretilor de compartimentare rezemati pe planseu;

tipul finisajelor aplicate;

limitarea / evitarea vibratiilor planseelor pentru:

planseele din beton armat cu deschideri mari in cladiri in care se petrec activitati care pot provoca vibratii (sali de gimnastica, sali de dans, etc);

planseele de lemn la toate categoriile de cladiri.

(3) Verificarea satisfacerii cerintei de rigiditate pentru plansee se face conform reglementarilor specifice pentru materialele respective.

8.3. Verificarea cerintei de stabilitate

Cerinta de stabilitate a cladirilor de zidarie este satisfacuta daca sunt respectate cerintele de alcatuire pentru ansamblul constructiei date la 2.2.3. si cerintele geometrice si de alcatuire constructiva pentru fiecare perete date in capitolele 5 si

8.4. Verificarea cerintei de ductilitate

Cerinta de ductilitate a peretilor din zidarie este considerata satisfacuta daca sunt realizate urmatoarele cerinte:

efortul unitar mediu de compresiune din incarcarile gravitationale se limiteaza la valori moderate (orientativ, circa 40% din rezistenta de proiectare la compresiune centrica);

sub efectul simultan al incarcarilor gravitationale si seismice:

se limiteaza adancimea zonei comprimate conform 3.3.(5);

armatura din zona intinsa reprezinta numai o fractiune din cantitatea corespunzatoare situatiei de 'balans' - conform 3.3.(3);

deformatia specifica in zidaria talpilor peretilor cu sectiuni compuse (L,T,I) se limiteaza la valoarea deformatiei ultime (e_zu) a elementelor pentru zidarie respective - conform 3.4.(1);

capacitatea de rezistenta la forta taietoare (care poate genera ruperi de tip fragil - ruperea din forta taietoare pe sectiuni in scara, de exemplu) - este superioara fortei taietoare asociata mecanismului de rupere ductil, sau mai putin fragil, din compresiune excentrica.