PROCEDEU SIMPLIFICAT DE CALCUL STRUCTURAL

Procedeu simplificat de calcul structural

In cazul cladirilor cu pana la 10 niveluri cu structuri ordonate si fara nesimetrii importante, la care peretii structurali prezinta monotonie geometrica se admite utilizarea procedeului de calcul structural simplificat descris in prezenta anexa.

Conditiile de monotonie structurala pe inaltimea cladirii presupun urmatoarele:

-caracteristicile geometrice si de material ale peretilor sunt constante pe inaltimea cladirii;

-inaltimile nivelurilor sunt egale;

-golurile sunt suprapuse si au aceleasi dimensiuni la toate nivelurile;

-incarcarile orizontale variaza pe inaltimea cladirii dupa o lege simpla (in general se admite distributia uniforma pentru incarcarile date de vant si distributia triunghiulara pentru incarcarile seismice conform fig.A.1.a).

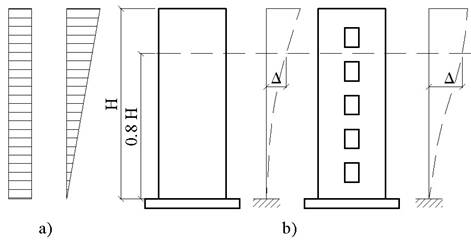
Fig.A.1

Procedeul este bazat pe aproximatia repartizarii incarcarilor orizontale intre peretii structurii pe baza conditiei de egalitate a deplasarilor orizontale la un singur nivel, ceea ce corespunde la a admite ipoteza ca deformatiile tuturor peretilor sunt afine. Se recomanda ca distributia fortelor orizontale sa se faca pe baza valorilor rigiditatilor la deplasarea laterala la nivelul caracteristic, considerat a fi situat la nivelul planseului cel mai apropiat de 0,8H (H = inaltimea cladirii, fig.A.1.b).

In conditiile admiterii ipotezelor simplificatoare de mai sus, incarcarile orizontale repartizate fiecarui perete structural pastreaza legea de variatie pe verticala admisa pentru incarcarea ansamblului structurii si ca atare fiecare perete poate fi calculat ca o structura monotona, pentru care pot fi stabiliti coeficienti pentru calculul direct al valorilor eforturilor sectionale si a deformatiilor.

Pentru incarcari orizontale aplicate centric pe structura (punctul de aplicatie al rezultantei coincide cu centrul de rigiditate al structurii), distributia intre peretii structurali se face proportional cu rigiditatile lor la deplasare laterala. In corelare cu schema de calcul adoptata, rigiditatea unui perete structural la deplasare laterala (r), pentru o incarcare orizontala distribuita pe verticala dupa o lege data, se defineste ca incarcarea orizontala necesara pentru a produce peretelui o sageata orizontala de 1 m la nivelul caracteristic.

Pentru incarcari orizontale aplicate excentric, distributia momentului de torsiune generala rezultat din excentricitatea rezultantei in raport cu centrul de rigiditate al structurii se face considerand, ca si in cazul aplicarii centrice, deplasarea solidara a peretilor pe baza ipotezei planseului infinit rigid in planul sau.

Din actiunea unui moment de torsiune generala M_t asupra ansamblului structurii (fig.A.2), un perete structural (j) se incarca cu o forta orizontala ale carei componente dupa directiile axelor Ox si Oy sunt F_jx si F_jy.

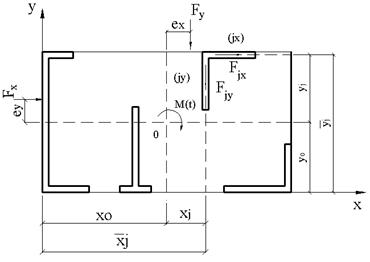
Fig.A.2

Sectiunile de calcul pe cele doua directii se stabilesc in conformitate cu indicatiile de la 5.2. Centrele de greutate corespunzatoare j_x si j_y se pot considera, de regula, cu suficienta aproximatie ca se afla in axul inimii de pe directia respectiva daca talpa este evazata nesimetric.

In schema de calcul, sectiunea unui perete structural apare deci cu centrele de greutate j_x si j_y diferite dupa cele doua directii, situate la distantele y_j si x_j in raport cu centrul de rigiditate 'o' al ansamblului. Fortele F_jx si F_jy se considera aplicate in j_x si j_y.

Alte notatii:

x_o, y_o - coordonatele centrului de rigiditate 0 in raport cu originea sistemului de axe;

- coordonatele centrelor de greutate ale sectiunilor de calcul ale peretelui ( j ) dupa directiile x si y in raport cu originea sistemului de axe;

- rigiditatile peretelui ( j ) la deplasari laterale dupa directiile x si y;

- sumele rigiditatilor pe ansamblul structurii:

(A.1)

I    - momentul de inertie la torsiune al ansamblului sectiunilor peretilor structurali, definit prin relatia:

(A.2)

F_x, F_y - rezultantele fortelor orizontale care actioneaza dupa directiile x si y;

e_x, e_y - excentricitatile in raport cu centrul de rigiditate (incluzand si excentricitatile aditionale prevazute de normativul P100/92).

Rigiditatile proprii ale peretilor structurali la torsiune se neglijeaza in calcul.

Rezulta ca o forta orizontala excentrica F_x , incarca peretele ( j ):

- dupa directia ( x ), cu forta:

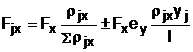(A.3)

- dupa directia ( y ), cu forta:

(A.4)

Similar, o forta orizontala F_y incarca peretele (j) :

- dupa directia ( x ), cu forta:

(A.5)

- dupa directia ( y ), cu forta:

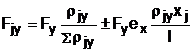(A.6)

Monotonia structurala si adoptarea unor legi simple pentru incarcarile orizontale permit o simplificare maxima a calculului.

In literatura exista numeroase lucrari, cu valori de calcul intabulate sau reprezentate grafic sub forma unor abace, care furnizeaza direct valorile caracteristicilor de rigiditate si ale eforturilor sectionale in pereti si grinzile de cuplare.