| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
In acest paragraf vom considera numai fortele centrale
![]() (1)
(1)
unde ![]() poate fi negativ (
poate fi negativ (![]() = - k) - deci forte de atractie - sau pozitiv (
= - k) - deci forte de atractie - sau pozitiv (![]() =k) - deci forte de respingere - (k>0)
=k) - deci forte de respingere - (k>0)
Euatia traiectoriei se poate obtine direct prin efectuarea integralei care intervine in ecuatia (1.25):
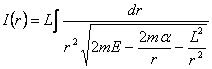 (2)
(2)
sau rezolvand ecuatia lui Binet. Integrala (2) se calculeaza
imediat efectuand schimbarea de variabila ![]() si obtinand
si obtinand
![]() (2')
(2')
care se pot transcrie sub forma
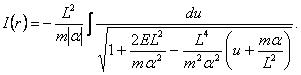 (2'')
(2'')
Ultima integrala, daca notam ![]() , este integrala bine cunoscuta
, este integrala bine cunoscuta
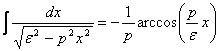 (3)
(3)
avand
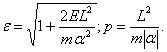 (4)
(4)
Deci
![]() -1
daca
-1
daca ![]()
![]() (5)
(5)
![]() 1 daca
1 daca ![]()
Convenind sa alegem ca semiaxa Cx semidreapta definita de centrul fortelor C si un punct particular al traiectoriei aflat la distanta minima rmin de centrul fortelor, depependenta unghiului de variabila r va fi data, in virtutea relatiilor (1.24) si (5), de
![]() . (6)
. (6)
de unde rezulta si relatia inversa
![]() (7)
(7)
sau explicit,
![]()
![]() pentru s<0
(forte de atractie)
pentru s<0
(forte de atractie)
![]() = (7')
= (7')
![]() pentru s>0
(forte de respingere).
pentru s>0
(forte de respingere).
Acelasi rezultat il obtinem rezolvand ecuatia Binet (1.33) care in cazul de fata este
![]() (1.33')
(1.33')
Aceasta este o ecuatie diferentiala de ordinul doi cu coeficienti constanti, neomogena, a carei solutie generala este suma dintre solutia generala a ecuatiei omogene corespunzatoare si o solutie particulara a ecuatiei neomogene. Astfel, solutia generala a ecuatiei (1.33') poate fi scrisa sub forma
![]() . (8)
. (8)
Cu aceeasi alegre a axei Cx ca in cazul stabilirii solutiei (7) vom avea
![]() (8')
(8')
si cerand ca
![]()
rezulta
![]() (8'')
(8'')
expresia lui ![]() in functie de
parametrii dati (m,l,E,
in functie de
parametrii dati (m,l,E,![]() ) obtinandu-se din ecuatia (1.27') care, in
cazul tratat aici, devine
) obtinandu-se din ecuatia (1.27') care, in
cazul tratat aici, devine
![]() (9)
(9)
avand radacinile
![]() (10)
(10)
Oricare ar fi semnul lui ![]() , umax este
, umax este
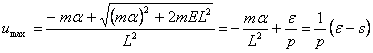 (10')
(10')
cu ![]() ,p definiti prin relatiile (4) si s
din ecuatia (5). Din ecuatiile (8'') si (10') obtinem
astfel
,p definiti prin relatiile (4) si s
din ecuatia (5). Din ecuatiile (8'') si (10') obtinem
astfel ![]() si folosind acest
rezultat in relatia (8') rezulta
solutia (7).
si folosind acest
rezultat in relatia (8') rezulta
solutia (7).
Ecuatia (7) este
forma cunoscuta a ecuatiei conicelor in coordonate polare. Parametrul
![]() se numeste
concentricitate si in functie de valorile acestuia se obtin cele
patru conice descrise de ecuatia (7) : elipsa (pentru 0<
se numeste
concentricitate si in functie de valorile acestuia se obtin cele
patru conice descrise de ecuatia (7) : elipsa (pentru 0<![]() <1), cercul (pentru
<1), cercul (pentru ![]() =0), hiperbola (pentru
=0), hiperbola (pentru ![]() >1) si parabola (pentru
>1) si parabola (pentru ![]() =1. Pentru a stabili acesta rezultate si a preciza
curbele corespunzatoare diferitelor conditii vom scrie ecuatia (7)
sub forma obisnuita in coordonate carteziene. Cu prcizarea
facuta privind alegerea axelor x,y scriem ecuatia (7) sub forma
=1. Pentru a stabili acesta rezultate si a preciza
curbele corespunzatoare diferitelor conditii vom scrie ecuatia (7)
sub forma obisnuita in coordonate carteziene. Cu prcizarea
facuta privind alegerea axelor x,y scriem ecuatia (7) sub forma ![]() si ridicand la
patrat ambii membri obtinem, dupa regruparea termenilor,
si ridicand la
patrat ambii membri obtinem, dupa regruparea termenilor,
![]() (11')
(11')
In cazurile in care ![]() ultima ecuatie
poate fi scrisa astfel
ultima ecuatie
poate fi scrisa astfel
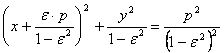 (12)
(12)
care, prin schimbarea de coordonate
![]() (12')
(12')
se reduce la forma canonica
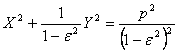 . (13)
. (13)
In noul sistem de axe, a carui origine o notam cu O, coordonatele centrului C al fortelor vor fi
![]() . (14)
. (14)
In cazul ![]() =1 ecuatia (11) revine la
=1 ecuatia (11) revine la
![]() (11')
(11')
care prin transformarea de coordonate
![]() (12'')
(12'')
devine
![]() (13')
(13')
iar coordonatele centrului C al fortelor in noul sistem de axe,
Din definitiile (4) se vede ca pentru ![]() avem
avem ![]() si in
functie de valorile energiei E,
si in
functie de valorile energiei E,
Din conditia (1.27) si ecuatia (9) cu radacinile (10) asa cum am constatat si din reprezentarea grafica a functiei Uef(r),rezulta urmatoarele:
-In cazul (15,a), E<0, (![]() ) care este
posibil numai daca
) care este
posibil numai daca ![]() (forte de
atractie) ecuatia (9) are doua radacini pozitive
distincte umin=1/rmax si umax=1/rmin
,conditia (1.27) fiind verificata numai pentru
(forte de
atractie) ecuatia (9) are doua radacini pozitive
distincte umin=1/rmax si umax=1/rmin
,conditia (1.27) fiind verificata numai pentru ![]() (traiectorie finita).
(traiectorie finita).
-In cazul (15,b), E>0, (![]() ) ecuatia (9) admite numai
o radacina pozitiva u=umax=1/rmin
si conditia (1.27) este verificata numai pentru
) ecuatia (9) admite numai
o radacina pozitiva u=umax=1/rmin
si conditia (1.27) este verificata numai pentru ![]() ; aceasta situatie este posibila indiferent de
sensul lui
; aceasta situatie este posibila indiferent de
sensul lui ![]() adica atat pentru
forte de atractie cat si pentru forte de respingere
(miscarea este nemarginita).
adica atat pentru
forte de atractie cat si pentru forte de respingere
(miscarea este nemarginita).
-Cazul (15,c), E=0, ![]() , nu este posibil decat pentru
, nu este posibil decat pentru ![]() (forte de
atractie). In acest caz conditia (1.27) devine
(forte de
atractie). In acest caz conditia (1.27) devine ![]() care se verifica
pentru
care se verifica
pentru ![]() adica
adica ![]() (este de asemenea
cazul unei miscarii nemarginite).
(este de asemenea
cazul unei miscarii nemarginite).
Sa analizam, in
continuare, traiectoriile in diferitele situatii definite in
relatiile (15) in functie de valorile parametrului ![]() .
.
a) ![]() . Asa cum am vazut, acest caz este posibil numai
daca fortele sunt de atractie (
. Asa cum am vazut, acest caz este posibil numai
daca fortele sunt de atractie (![]() ),miscarea fiind caracterizata prin traiectorie
finita. Ecuatia (13) a traiectoriei va fi
),miscarea fiind caracterizata prin traiectorie
finita. Ecuatia (13) a traiectoriei va fi
unde introducem notatiile si rezultatele mai generale
utile si pentru cazurile urmatoare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1080
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved