| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Functii reale, de una sau mai multe variabile,
cu valori scalare sau vectoriale. Multimi de definitie.
Functii liniare. Functii patratice
I
I.1) Fie ![]() . Sa se demonstreze ca sunt adevarate
urmatoarele relatii:
. Sa se demonstreze ca sunt adevarate
urmatoarele relatii:
a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ;
;
d) ![]() -
- ![]() ; e)
; e) ![]() ; f)
; f) ![]() .
.
(![]() reprezinta notatia pentru functia
caracteristica a multimii A)
reprezinta notatia pentru functia
caracteristica a multimii A)
I.2) Fie ![]() o functie cu
urmatoarele proprietati:
o functie cu
urmatoarele proprietati:
i) ![]() ,
,
ii) ![]() ,
,
iii)
![]() ,
,
iv) ![]() .
.
Sa se arate ca ![]() este o topologie pe
este o topologie pe ![]() si, in
spatiul topologic
si, in
spatiul topologic ![]() , avem
, avem ![]() ,
, ![]() .
.
II
II.1) Sa se stabileasca multimile de definitie ale urmatoarelor functii reale:
a) ![]() ; b)
; b) ![]() ;
;
c) ![]() ; d)
; d) ![]() ;
;
e) ![]() ; f)
; f) ![]() ;
;
g) ![]() ; h)
; h) ![]() .
.
i) ![]() ;
;
j) ![]() ;
;
k) ![]() .
.
II.2) Sa se gaseasca imaginea geometrica a multimii de definitie in cazul urmatoarelor functii reale:
a)
![]() ; b)
; b) ![]() ;
;
c)
![]() ; d)
; d) ![]() .
.
III.1) Care din urmatoarele functii reale sunt liniare?
a) ![]() ,
, ![]() ;
;
b) ![]() ,
, ![]() ;
;
c) ![]() ,
, ![]() ;
;
d) ![]() ,
, ![]() ;
;
e) ![]() ,
, ![]() .
.
Sa se rescrie, matriceal, expresiile acelor functii care sunt liniare (in raport cu bazele canonice in cauza).
III.2) Sa se verifice ca urmatoarele functii
liniare reprezinta transformari punctuale ortogonale de la ![]() la
la ![]() :
:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
III.3) Sa se studieze posibilitatea diagonalizarii urmatoarelor functii liniare reale:
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d)
![]() .
.
IV
IV.1) Sa se stabileasca natura, indicele pozitiv si signatura pentru fiecare din urmatoarele functii patratice:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) 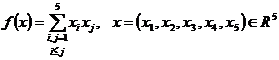 .
.
IV.2) Sa se gaseasca forma canonica a urmatoarelor functii patratice:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]() .
.
IV.3) Sa se determine parametrul real ![]() astfel incat
functiile patratice urmatoare sa fie pozitiv (respectiv
negativ) definite:
astfel incat
functiile patratice urmatoare sa fie pozitiv (respectiv
negativ) definite:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
IV.4) Sa se
stabileasca entitatea geometrica din ![]() sau
sau ![]() descrisa de
fiecare din ecuatiile / sistemele de ecuatii polinomiale (de gradul I
sau II) de mai jos:
descrisa de
fiecare din ecuatiile / sistemele de ecuatii polinomiale (de gradul I
sau II) de mai jos:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) 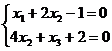 ; e)
; e) ![]() ;
;
f) ![]() ;
;
g) ![]() ;
;
h) ![]() ;
;
i) ![]() ;
;
j) ![]() ;
;
k) ![]() ;
;
l) ![]() ;
;
m) ![]() ;
;
n) ![]() ;
;
o) ![]() .
.
F. Iacob / 01.10.2006
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2142
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved