| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Inegalitati referitoare la unghiurile unui triunghi
Aplicatia
II.3.1: Fie triunghiul ABC cu ![]() . Sa se arate ca
. Sa se arate ca ![]() si
si ![]() .
.
Solutie:
Fie triunghiul ABC cu ![]() . Cum
. Cum ![]() , deducem ca:
, deducem ca:
![]() si deci
si deci ![]() , iar
, iar![]() , ceea ce implica
, ceea ce implica
![]() si
si ![]() .
.
Aplicatia II.3.2: Demonstrati ca:
Daca ![]() ,
, ![]() ,
, ![]() si
si ![]() atunci
atunci
1) ![]()
2) ![]()
Solutie:
Vom aplica inegalitatea Jensen si anume:
![]() Consideram
functia
Consideram
functia ![]() pe segmentul
pe segmentul ![]() . Pe acest segment functia este concava conform
definitiei clasice, intrucat
. Pe acest segment functia este concava conform
definitiei clasice, intrucat ![]() , pentru
, pentru ![]() . Luand doua puncte
. Luand doua puncte ![]() , functia
, functia ![]() devine
devine ![]()
![]() adica
adica ![]() .
.
Inegalitatea Jensen aplicata pentru ![]()
![]() si
si ![]() ;
; ![]() ; ne da
; ne da ![]() .
.
Daca luam ![]() ,
, ![]() ,
, ![]() cu
cu ![]() ;
;
![]() avem
avem ![]() de unde
de unde
![]() . In mod analog se demonstreaza si a doua
relatie.
. In mod analog se demonstreaza si a doua
relatie.
Aplicatia
II.3.3: Sa se arate ca: ![]()
Solutia 1:
Stim ca ![]() . Am aplicat inegalitatea mediilor
. Am aplicat inegalitatea mediilor ![]() ;
;
Solutia 2:
![]()
![]() deci
deci ![]() .
.
Aplicatia
II.3.4: Fie triunghiul ABC cu x,y,z masurile unghiurilor ![]() ,
, ![]() ,
, ![]() , in radiani
atunci:
, in radiani
atunci: ![]() unde a,b,c sunt
lungimile laturilor triunghiului.
unde a,b,c sunt
lungimile laturilor triunghiului.
Solutie:
Stim ca ![]() , atunci
, atunci ![]() deci
deci ![]() ;
; ![]() ;
; ![]()
Insumam si obtinem:
![]() , deci
, deci ![]() deci:
deci: ![]()
Daca ![]() , avem inegalitatea evidenta:
, avem inegalitatea evidenta: ![]() .
.
Dar ![]() deci
inegalitatile sunt demonstrate.
deci
inegalitatile sunt demonstrate.
Aplicatia
II.3.5: Sa se demonstreze ca intr-un triunghi ABC: ![]()
Solutie:
Din teorema sinusului avem: 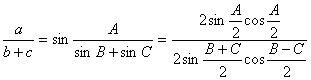 . Dar
. Dar ![]() . Deci dupa simplificare obtinem:
. Deci dupa simplificare obtinem:
![]() .
.
Aplicatia
II.3.6: Sa se demonstreze ca un triunghi este ascutitunghic
daca si numai daca: ![]() .
.
Solutie:
Din egalitatea II.1.1.15 ![]() si teorema
sinusurilor
si teorema
sinusurilor ![]() , rezulta:
, rezulta: ![]() .
.
Daca ![]() rezulta
rezulta ![]() , adica triunghiul este ascutitunghic. Daca
triunghiul este ascutitunghic, atunci avem:
, adica triunghiul este ascutitunghic. Daca
triunghiul este ascutitunghic, atunci avem: ![]() si cum
si cum ![]() .
.
Aplicatia
II.3.7: Sa se demonstreze ca intr-un triunghi: ![]() .
.
Solutie:
Conform relatiei de egalitate din problema precedenta avem:
![]() . Din inegalitatea
. Din inegalitatea ![]() , rezulta:
, rezulta:
![]() .
.
Aplicatia II.3.8: Sa se demonstreze ca intr-un triunghi ascutitunghic:
![]() .
.
Solutie:
Intr-un triunghi ascutitunghic putem sa avem una si numai una din variante:
![]() sau
sau ![]() . In ambele cazuri
avem:
. In ambele cazuri
avem:
![]() .
.
Deoarece ![]() avem:
avem: ![]() .
.
Dar ![]() sau
sau ![]() , deci
, deci ![]() .
.
Dar ![]() . Inlocuind avem:
. Inlocuind avem: ![]() sau
sau ![]() , deci
, deci ![]() .
.
Observatie: Daca in inegalitatea din enunt inlocuim cu egalitatea II.1.1.14
![]() si teorema
sinusurilor
si teorema
sinusurilor ![]() , obtinem
, obtinem ![]() sau
sau ![]() .
.
Aplicatia II.3.9: Sa se demonstreze ca intr-un triunghi oarecare avem:
![]()
Solutie:
Rezolvam problema prin dualitate. Fie un triunghi oarecare ABC.
Atunci exista triunghiul ascutitunghic ![]() cu unghiurile
cu unghiurile ![]() ;
; ![]() ;
;  . Aplicand inegalitatea din problema precedenta avem:
. Aplicand inegalitatea din problema precedenta avem:
![]() si inlocuind
obtinem:
si inlocuind
obtinem: ![]() .
.
Aplicatia
II.3.10 J.M. Child: Intr-un triunghi oarecare, ![]() .
.
Solutie:
Din problema II.3.5 rezulta ![]()
![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1331
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved