| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Sa consideram polinomul
![]() ai
Z
ai
Z ![]()
si din formula lui Taylor referitoare la dezvoltarea lui f in α, avem
![]()
Restul impartirii polinomului f la x - α este f (α). Deci restul impartirii lui
![]()
la x - α este f'(α).
Continuand procedeul avem
![]()
Restul impartirii lui S2(x) la x - α este f'' (α) s.a.m.d. Acest fapt ne sugereaza o generalizare a schemei lui Horner in felul urmator.
Fie
a , a1, a2, ., an-1, an
coeficientii lui f.
Deci a'0, a'1, a'2, ., a'n-1 vor fi coeficientii lui f '(α) dati de
a'0 = a0, a'1 = a'0 α + a1, ., a'n-1 = a'n-2 α + an-1
a'n-1 fiind chiar valoarea lui f '(α).
Continuand, obtinem a"0, a"1, a"2, ., a"n-2 unde
a"0 = a'0, a"1 = a"0 α + a'1, ., a"n-2 = a"n-3 α + a'n-2, s.a.m.d.
Deci ![]() va fi a"n-2 s.a.m.d.
va fi a"n-2 s.a.m.d.
Acest fapt ne permite urmatoarea reprezentare

unde a0, a11, . , a1,n-2, a1,n-1 au semnificatia lui a'0, a'1, a'2, ., a'n-1 s.a.m.d. Acest algoritm permite o metoda de calcul al unei radacini irationale separata intre doua numere intregi consecutive a si a + 1.
Fie o ecuatie algebrica de grad n
f (x) = 0.
Sa presupunem ca am separat o radacina reala x si numai una singura intre doua numere intregi consecutive pozitive a si a + 1.
Facem transformarea ![]() R, x1 > 1 si obtinem ecuatia
R, x1 > 1 si obtinem ecuatia
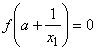
sau
![]()
care are o unica radacina pozitiva strict mia mare decat 1. Prin urmare exista b N , b ≥ 1 astfel incat x1 se afla intre b si b + 1.
Continuam procedeul de calcul si avem
![]() R, x2
> 1
R, x2
> 1
si formam ecuatia
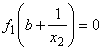
sau
![]() s.a.m.d.
s.a.m.d.
Se obtine deci
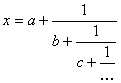
Daca x este rational, fractia continua este finita si una din transformatele succesive va aminti o radacina intreaga.
Daca x este un numar irational fractia continua va fi infinita. In acest caz procedeul va continua pana cand va fi indeplinita conditia data de teorema lui Dirichlet si anume
![]()
unde Ri reprezinta redusa de rang i in dezvoltarea lui x in fractie continua regulata, Bi numitorul redusei de rang i, iar ε precizia dorita.
Observatie 4.7.1 Din punct de vedere calculatoriu putem utiliza metoda Lagrange pentru obtinerea primelor cifre ale radacinii cautate si apoi aproximatia gasita sa o folosim drept valoare initiala in metoda Newton (tangentei).
Observatie 4.7.2 Calculul radacinilor negative ale ecuatiei f (x) = 0 se reduce la determinarea radacinilor pozitive ale ecuatiei f (- x) = 0.
Exemplu 4.7.1 Sa se rezolve ecuatia
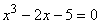
folosind metoda lui Lagrange.
Solutie. Avem f (2) = 8 - 4 - 5 = - 1 < 0 si f (3) = 27 - 6 - 5 = 16 > 0. Deci
![]()
Calculam
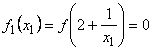
Calculam coeficientii lui f 1 dupa schema lui Horner generalizata pentru α = 2:

Deci
![]()
sau ![]() se mai poate scrie
se mai poate scrie
![]()
adica
![]()
Deci
![]() si
si ![]()
Deci
![]()
 Deci avem
Deci avem

![]()
sau
![]()
Radacina va fi cuprinsa intre 1 si 2. Deci
![]()
Deci


![]()
Deci
![]()
cu 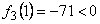 si
si ![]()
Facem transformarea
![]()
si avem dupa calcule asemanatoare
![]()
![]() si
si ![]() .
.
Deci
![]()
si avem
![]()
cu ![]() si
si ![]() .
.
Punem
![]()
si obtinem
![]()
![]() si
si ![]() .
.
Deci
![]()
si avem
![]()
Deci ![]() si
si ![]() . Urmeaza
. Urmeaza
![]()
![]()
![]() si
si ![]()
![]()
![]()
![]() si
si 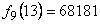
si
![]()
Redusele lui x vor fi succesiv
![]()
![]()
Aproximand pe x prin redusa R 9 eroarea absoluta, data de Teorema lui Dirichlet, va fi
![]()
adica x este calculat cu 9 zecimale exacte
x
Programul pentru metoda Lagrange
Programul determina cea mai mica solutie pozitiva si cea mai mare solutie negativa pentru o ecuatie algebrica (daca acestea exista) prin metoda Lagrange.
Numarul de iteratii folosit este definit (dar poate fi modificat) in program prin variabila mmax si este considerat criteriu de oprire.
Datele de intrare sunt gradul si coeficientii polinomului.
# include <iostream .h>
# include <math .h>
# include <conio .h>
# include <stdlib .h>
# include <iomanip .h>
int semn=1, n, i, mmax=20;
double xmax=100000.0, x0[100], a[100], b[100];
long double xx;
void date (void)
}
double f ( double x)
double xi (int m)
void fi (double x)
}
void main (void)
else
else
fi (x0[m]);
}
}
while ((m<=mm)&&(test = = 0));
if (test != -1)
for (i=0; i<=n; i++)
m = 0; mm = mmax; test = 0;
do
else
else
fi (x0[m]);
}
}
while ((m<=mm)&&(test = = 0));
xx = x0[mm];
for (m=mm-1; m>=1; m--)
xx = x0[m]+1/xx;
cout<<"Solutia negativa x = "<<setprecision(10)<<-xx;
getch( );
}
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2312
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved