PROBLEME REZOLVATE . PARALELOGRAM

PROBLEME REZOLVATE . PARALELOGRAM

1. Fie ABCD un paralelogram si O intersectia diagonalelor. Prin O se duce o dreapta oarecare care intersecteaza AB si CD in M, respectiv N. Sa se demonstreze ca MO si NO sunt congruente.

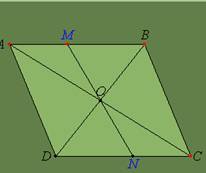
Rezolvare.

ABCD= paralelogram si O intersectia diagonalelor, rezulta ca diagonalele se injumatatesc, deci BO=DO.
Comparam triunghiurile BOM si DON, gasind: BO=DO (dem), <B=<D (alt-int:AB||CD, sec.BD), <MOD=<DON (opuse la varf), deci, conform cazului ULU, cele doua triunghiuri sunt congruente, de unde MO=NO, fiind laturi omoloage in triunghiuri congruente.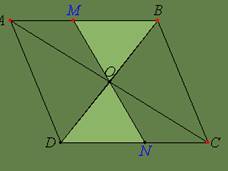

Se considera punctele M si N pe laturile AB, BC ale paralelogramului ABCD si O intersectia diagonalelor. Daca P este intersectia dintre MO si CD iar Q este punctul de intersectie dintre NO si DA, sa se arate ca MNPQ este paralelogram.

Rezolvare

Comparand tr.AOM cu tr.COP avem:(AO)º (OC)(O=mijl.AC);<AOM º <POC (op. vf.); <OAM º <OCP (alt.-int.:AB // CD, sec.AC) Þ (PO) º (MO)

Comparand trAOQ cu trCON avem :(AO)º (OC) (O=mijl.AC); <AOQº <CON (op. vf.); <QAOº <NCO (alt.-int.:AD // BC,sec.AC)Þ (OQ)º (ON).

Din (OQ)º (ON) si (OM)º (OP)Þ MNPQ=paralelogram (diagonalele se injumatatesc).

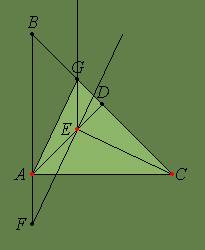
In triunghiul ABC dreptunghic in A, fie E un punct pe inaltimea AD. Paralela prin E la AB intersecteaza BC in G, iar perpendiculara in E pe CE intersecteaza pe AB in F. Sa se arate ca AGEF este paralelogram.

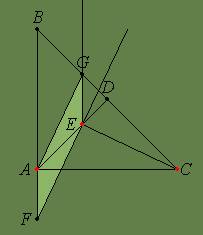
Rezolvare

• Din GE // AB si AB AC Þ GE AC.
• In trAGC, GE AC si AD GC, deci E este ortocentrul triunghiului, prin urmare CE AG.
• Deoarece CE AG si CE EF Þ EF//AG.
• Din EF//AG si AF//GE (ip.)Þ AGEF=paralelogram.

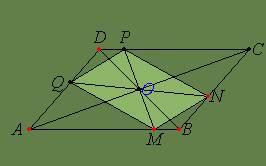
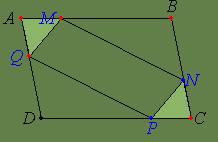
Pe laturile AB si CD ale paralelogramului ABCD, se iau punctele M, respectiv P astfel incat m[AM]=m[CP], iar pe laturile AD si BC se iau punctele Q, respectiv N astfel incat m[AQ]=m[CN]. Sa se demonstreze ca MNPQ este paralelogram.

Rezolvare

Comparam trAMQ cu trCPN si avem <A º <C (opuse in par.), [AM] º [CP] (ip), [AQ] º [CN] (diferente de segmente congruente). Conform cazului LUL, trAMQ º trCPN, deci [QM] º [PN].

Comparam trDPQ cu trBMN si avem <B º <D (opuse in par.), [BM] º [DP] (diferente de segmente congruente), [DQ] º [BN] (diferente de segmente congruente). Conform cazului LUL, trDPQ º trBMN, deci [PQ] º [MN].    Din [PQ] º [MN] si [PN] º [PQ], obtinem ca MNPQ este paralelogram, avand laturile opuse congruente

Fie E un punct pe diagonala BD a paralelogramului ABCD si CF||AE (F apartine lui BD). Sa se demonstreze ca AECF este paralelogram.

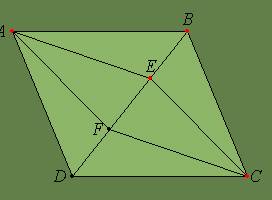
Rezolvare

Din CF // AE (ip) si AD // BC (lat. op. in par) obtinem ca <DAEº <BCF(unghiuri cu laturi paralele).

Comparam trDAE cu trBCF (AD=CE, <DAEº <BCF, <ADEº <FBC, alt-int), conform cazului ULU Þ tr DAEº tr CBFÞ AEº CF.

Din AE||CF si AEº CF Þ AECF=paralelogram (avand doua laturi paralele si congruente).

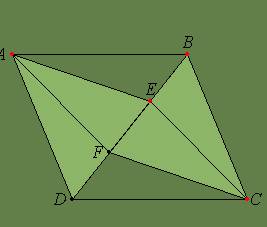
Fie BE si CF perpendicularele din B si C pe mediana AD a triunghiului ABC. Sa se demonstreze ca BECF este paralelogram.

Rezolvare

Dreptele BE si CF fiind perpendiculare pe AD rezulta ca BE // CF.

In patrulaterulul BECF: BE // CF si diagonala EF trece prin mijlocul diagonalei BC (pt ca AD este mediana in triunghiul ABC), rezulta ca BECF este paralelogram.