Caracterizarea marimilor sinusoidale. Studiul circuitelor de curent alternativ sinusoidal prin metoda directa.

Caracterizarea marimilor sinusoidale. Studiul circuitelor de curent alternativ sinusoidal prin metoda directa.

Marimile variabile sunt marimi fizice (t.e.m., caderi de tensiuni, intensitati ale curentului electric etc.) care isi modifica valoarea in timp.

Marimea alternativa este o marime variabila a carei succesiune de valori se repeta la intervale egale de timp.

Marimea alternativa este o marime periodica a carei valoare medie pe timpul unei perioade este nula.

Marimea pulsatorie este o marime variabila a carei valoare instantanee pastreaza tot timpul acelasi semn.

Marimea sinusoidala sau armonica este o marime alternativa care poate fi scrisa sub forma

Marimile sinusoidale se caracterizeaza prin:

Valoarea instantanee, este valoarea pe care o are marimea sinusoidala in fiecare moment. Prin conventie, valoarea instantanee se noteaza cu litera mica, astfel: etc.

Periodicitatea, data de perioada marimilor sinusoidale T, respectiv frecventa acestora f (sau ν). Periodicitatea se exprima printr-o relatie de forma:

, unde k=1, 2, , n.

Perioada T reprezinta intervalul minim de timp dupa care valorile unei marimi sinusoidale se reproduc in aceeasi ordine.

Frecventa f unei marimi sinusoidale este numarul de oscilatii complete, ale marimii sinusoidale, cuprins in unitatea de timp (sec.):

Pulsatia marimii sinusoidale este o caracteristica importanta legata de periodicitatea ei si este data de relatia:

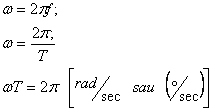
Pulsatia se mai numeste si frecventa unghiulara.

Marimea () poarta numele de faza marimii sinusoidale. Daca oscilatia unei marimi alternativ nesinusoidale nu incepe odata cu momentul t=0(moment cand incepe observatia sau masurarea), atunci este nevoie sa se introduca o marime suplimentara, notati in cazul curentului cu , care se numeste faza initiala. Faza initiala poate fi pozitiva sau negativa. Faza marimii sinusoidale este argumentul sinusului, adica marimea liniar variabila in timp (

Valoarea de varf este cea mai mare valoare instantanee atinsa de o marime periodica in decurs de o perioada. Valoarea de varf se noteaza cu , etc.

Valoarea medie, reprezinta media pe o perioada a valorilor instantanee ale marimilor sinusoidale. De exemplu, valoarea medie a curentului este:

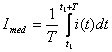(6.17)

Valoarea medie, care are in general valori pozitive sau negative pentru marimile periodice, este nula in cazul unei marimi alternativ sinusoidale (fig 6.5).

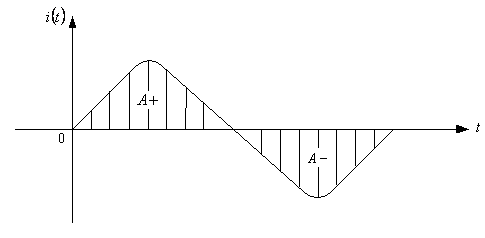
Fig. 6.5

Astfel se observa din figura (6.5) ca suma algebrica a ariilor cuprinse de cele doua oscilatii, pozitiva si negativa, este zero:

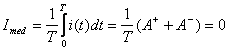
Se utilizeaza totusi, pentru caracterizarea valorilor sinusoidale (6.18) o valoare medie calculata numai pentru semiunda pozitiva:

(6.18)

Valoarea efectiva sau valoarea eficace este valoarea calculata cu radacina patrata a mediei patratelor valorilor instantanee a unei marimi sinusoidale in decurs de o perioada.

Are expresia:

(6.19)

Interpretarea fizica a valorilor efective (sau eficace) este urmatoarea:

valoarea efectiva a unui curent sinusoidal este numeric egala cu intensitatea unui curent continuu, care strabatand aceeasi rezistenta ca si curentul sinusoidal, produce aceeasi cantitate de caldura in timp de o perioada.

Valoarea efectiva a unei marimi sinusoidale se noteaza cu litera mare (I,U, etc) la fel ca marimea respectiva in curent continuu.

Aparate electrice de masurat, industriale, indica valoarea efectiva a marimilor sinusoidale.

Relatia dintre valoarea efectiva si valoarea maxima;

Daca se ridica la patrat expresia valorii efective:

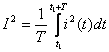
si se inlocuieste valoarea instantanee i(t) cu expresia sinusoidala:

se obtine

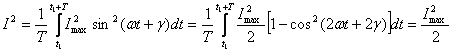
Astfel relatia dintre cele doua valori este:

In mod similar, valoarea efectiva a unei tensiuni este:

Raportul intre valoarea efectiva si valoarea medie (calculata pentru semiunda pozitiva) a unei marimi sinusoidale se numeste factor de forma al undei:

(6.21)

Pentru un curent sinusoidal factorul de forma are valoarea:

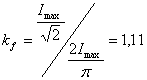(6.22)

In electrotehnica se opereaza cu valorile efective ale marimilor sinusoidale. Tinand seama de caracteristicile aratate, o marime sinusoidala va avea expresia generala de forma:

(6.23)

Aceasta expresie poarta numele de forma normala in sinus a marimii sinusoidale. Ca urmare, o marime sinusoidala este complet determinata cand se cunosc:

frecventa (f), sau pulsatia (ω);

valoarea efectiva (I, U);

faza initiala (γ, β)

Diferenta dintre fazele initiale ale doua marimi sinusoidale de aceeasi frecventa se numeste defazaj.

Pentru doua marimi sinusoidale de forma: si , defazajul este :

(6.24)

Daca , curentul este defazat inaintea lui (fig. 6.6.a).

Daca , curentul este defazat in urma lui (fig. 6.6.b).

Marimile si sunt in faza daca

In mod similar se poate defini defazajul dintre doua tensiuni sau dintre tensiune si un curent.

Defazajul maxim dintre tensiune si curent este de , pe cand intre doua tensiuni sau doi curenti este de

Cand marimile sunt in cuadratura.

Cand marimile sunt in opozitie de faza.

Cand marimile sunt in faza.

Fig.6.6

Circuitele liniare de curent alternativ sunt descrise de ecuatii integro diferentiale liniare in care, asupra marimilor sinusoidale se fac operatiile de adunare, inmultire cu un scalar, derivare sau integrare in raport cu timpul.

Cum marimile rezultante sunt de asemenea sinusoidale si cu aceeasi frecventa, acest lucru constituie un avantaj in utilizarea metodelor operationale, cum ar fi aceea a reprezentarii in complex.

a) Adunarea marimilor sinusoidale, si conduce la o marime sinusoidala de forma:

Prin identificare: se obtine:

(6.25)

(6.26)

b) Amplificarea unei marimi sinusoidale cu un scalar conduce la o marime sinusoidala de aceeasi frecventa si aceeasi faza initiala, dar cu valoare efectiva amplificata de ori:

(6.27)

c) Derivarea unei marimi sinusoidale in raport cu timpul conduce la o marime sinusoidala de aceeasi frecventa, dar defazata cu si avand valoarea efectiva de ori mai mare.

(6.28)

d) Integrarea in timp a unei marimi sinusoidale conduce la o marime sinusoidala de aceeasi frecventa, dar defazata in urma cu si avand valoarea efectiva de ori mai mica. Daca atunci integrala acesteia este:

(6.29)

Metoda directa de analiza a circuitelor electrice in regim permanent sinusoidal consta in scrierea ecuatiei integro-diferentiale a circuitului si cautarea unei solutii particulare a acesteia, de aceeasi forma cu tensiunea aplicata la borne. Metoda se aplica numai circuitelor liniare.

Se considera ca la bornele unui circuit simplu, liniar, se aplica o tensiune alternativa sinusoidala de forma (fig. 6.7):

(6.30)

Fig.6.7

Se cere sa se gaseasca expresia curentului din circuit.

Prin scrierea ecuatiei circuitului si rezolvarea acesteia rezulta curentul i(t) de forma:

(6.31)

similara cu cea a tensiunii aplicate la borne.

Prin conventie se noteaza cu φ defazajul dintre u(t) si i(t):

(6.32)

Prin conventie se introduce marimea Z, numita impedanta circuitului in raport cu cele doua borne de acces in exterior, sub forma:

(6.33)

unde U si respectiv I sunt valorile efective ale tensiunii si curentului, iar asocierea sensurilor de referinta se face dupa regula de la receptoare.

Unitatea de masura a impedantei este ohm-ul (Ω).

Ca urmare:   

si (6.34)

Expresia curentului la bornele circuitului devine (in valoare instantanee):

(6.35)

In relatia (6.35) toate valorile marimilor din membrul drept sunt cunoscute, deci poate fi determinata valoarea curentului din circuitul analizat.

In continuare vor fi rezolvate circuite simple R, L, C precum si un circuit serie R-L-C prin metoda directa.

Circuit cu rezistor ideal (fig. 6.8)

Fig.6.8

Ecuatia circuitului, alimentat cu tensiunea la borne u(t) este unde

Rezulta expresia curentului prin circuit:

(6.37)

Cum i(t) trebuie sa fie de forma tensiunii la borne (circuitul fiind considerat liniar), adica:

(6.38)

Prin compararea relatiilor (6.36) si (6.37) rezulta:

(6.39)

Rezistorul ideal are impedanta egala cu rezistenta sa, iar defazajul dintre tensiune si curent este nul (tensiunea si curentul sunt in faza).

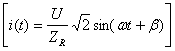
Circuit cu bobina ideala (fig. 6.9)

Fig.6.9

Ecuatia circuitului, alimentat pe la borne cu o tensiune sinusoidala are expresia:

(6.40)

Curentul i(t) din circuit se obtine integrand relatia de mai sus (6.40):

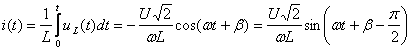(6.41)

Cum i(t) va trebui sa fie de forma:

(6.42)

deoarece circuitul este presupus liniar, rezulta prin compararea relatiilor (6.41) si (6.42):

(6.43)

Bobina ideala are impedanta proportionala cu frecventa tensiunii aplicate, iar defazajul dintre tensiune si curent este de . Se spune ca tensiunea unei bobine ideale este defazata inaintea curentului cu

Circuit cu condensator ideal (fig. 6.10)

Fig.10

Ecuatia circuitului alimentat pe la borne cu tensiunea sinusoidala are expresia:

(6.44)

Prin diferentiere va rezulta expresia curentului din circuit sub forma:

(6.45)

Cum i(t) trebuie sa fie de forma:

(6.46)

deoarece circuitul este presupus liniar (i se poate aplica teorema capacitatii: ), prin compararea relatiilor (6.45) si (6.46) rezulta:

(6.47)

Condensatorul ideal are impedanta invers proportionala cu frecventa tensiunii aplicate la borne si defazeaza tensiunea in urma curentului cu (respectiv defazajul este de

Circuit serie cu R-L-C ideale (fig. 6.11)

Fig.6.11

Ecuatia circuitului alimentat pe la borne cu tensiunea sinusoidala are expresia:

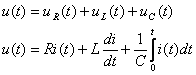(6.48)

Cum circuitul este liniar curentul prin circuit va trebui sa fie de forma tensiunii la borne:

(6.49)

Inlocuind expresia curentului in relatia (6.48) se obtine:

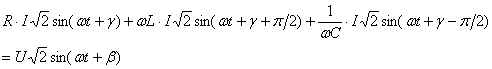(6.50)

Pentru rezolvarea ecuatiei (6.50) se introduc conditiile particulare:

Obtinandu-se relatiile:

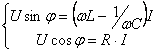(6.51)

Ridicand la patrat si adunand cele doua ecuatii (6.51) rezulta curentul I si impedanta Z:

(6.52)

Impartind cele doua relatii se obtine defazajul φ:

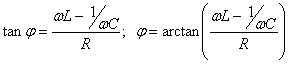(6.53)

Ca urmare curentul i(t) devine:

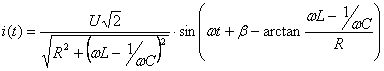(6.54)

In cazul circuitului mixt R, L, C, defazajul φ este cuprins intre si , in functie de preponderenta inductantei sau a capacitatii. Defazajul este pozitiv cand circuitul este preponderent inductiv (adica impedanta bobinei ideale este mai mare decat cea a condensatorului ideal

In primul caz (Z_L > Z_C) tensiunea este defazata inaintea curentului (φ>0), iar in al doilea caz (Z_L < Z_C) tensiunea este defazata in urma curentului (φ<0).