Coduri Hamming ciclice

1. Obiectivul lucrarii

Lucrarea se ocupa cu studiul codurilor Hamming ciclice corectoare de o eroare/detectoare de doua erori, codate si decodate prin circuite de divizare si registre de deplasare cu reactie.

2. Introducere teoretica

Codurile ciclice sunt coduri bloc in care cele n simboluri care formeaza un cuvant sunt considerate ca fiind coeficientii binari ai unui polinom v(x) de grad n-1.

Codurile ciclice au proprietatea ca daca v(x) este un cuvant cu sens, atunci orice permutare ciclica a simbolurilor sale este un cuvant cu sens.

De asemenea, cuvintele de cod sunt privite ca elemente ale unei algebre lineare (+,x) modulo p(x) = xⁿ + 1. Cuvintele cu sens (in numar de 2^k) sunt elemente ale idealului generat de polinomul ireductibil si primitiv g(x)    (numit polinom generator, divizor al polinomului p(x)) de grad m:

v(x) = i(x)g(x),

iar cuvintele fara sens (in numar de 2ⁿ - 2^k) alcatuiesc cele 2^m clase de resturi modulo p(x).

Relatiile matriceale deduse in cazul codurilor grup raman valabile, codurile ciclice facand parte, de asemenea, din categoria codurilor lineare.

Codarea este operatia de determinare a polinomului simbolurilor de control c(x) in functie de polinomul simbolurilor de informatie i(x). Simbolurile de control introduc o redundanta care faciliteaza detectia si corectia erorilor. Acestea pot fi calculate pe baza polinomului generator g(x), din relatia:

sau pe baza polinomului de control h(x) de grad k, din relatia

v(x)h(x) = 0 modp(x),

in ambele cazuri rezultand un cuvant de cod de forma:

Polinomul de control poate fi determinat din polinomul modulo si polinomul generator cu relatia:

Cu ajutorul coeficientilor polinomului de control, matricea H poate fi scrisa astfel:

.

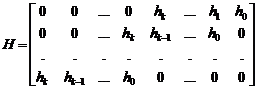Codul Hamming ciclic este un cod perfect (n = 2^m-1), corector de o eroare (d_min = 3) si sistematic, adica are proprietatea ca simbolurile de informatie sunt delimitate de simbolurile de control si sunt plasate succesiv la sfarsitul cuvantului de cod.

Decodarea este operatia inversa codarii si consta in gasirea unei corespondente intre cuvantul eronat receptionat v'(x) si erorile introduse de canal e(x):

v'(x) = v(x) + e(x).

Decodarea se face pe baza valorii corectorului s(x)

care se obtine prin insumarea simbolurilor de control receptionate cu simbolurile de control obtinute prin recodarea simbolurilor de informatie receptionate:

Codurile ciclice cu distanta minima 3 pot fi utilizate fie pentru corectia erorilor singulare, fie pentru detectia erorilor duble. In ambele cazuri, se prelucreaza valoarea corectorului, folosindu-se diverse circuite pentru efectuarea codarii si a decodarii.

2.1. Codarea prin circuite de divizare

Codorul este format dintr-un circuit de divizare cu celule binare de memorare pe 1 bit si sumatoare modulo 2 interioare. Circuitul de divizare are conexiunile buclei de reactie realizate conform coeficientilor polinomului generator g(x).

Schema bloc este prezentata in figura 1.

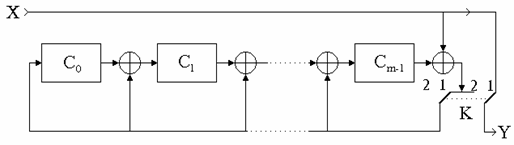
Fig. 1. Codor cu circuit de divizare prin g(x).

Pe durata primelor k perioade de tact, comutatorul K este in pozitia 1, astfel incat cei k biti de informatie de la intrare se regasesc in cuvantul de la iesire. Celulele codorului vor contine dupa k perioade de tact simbolurile de control.

Dupa terminarea introducerii simbolurilor de informatie, comutatorul K este trecut in pozitia 2 si continutul celulelor este evacuat, completandu-se ultimii m biti din cuvantul de cod, care reprezinta simbolurile de control.

2.2. Decodare cu circuite de divizare

2.2.1. Detectia erorilor

Decodorul cu detectia erorilor este eficient pentru detectia pachetelor de erori de lungime maxima m. Schema bloc este prezentata in figura 2.

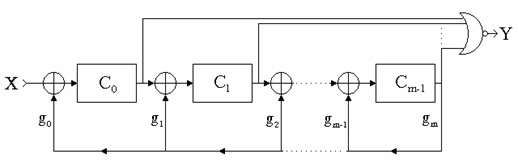
Fig. 2. Decodor cu circuit de divizare pentru detectia erorilor.

Dupa n perioade de tact, in circuitul de divizare se va afla restul impartirii polinomului cuvantului receptionat la polinomul generator g(x). Daca acest rest este 0, la iesirea portii SAU-NU va fi "1", deci cuvantul receptionat nu este eronat. Iesirea portii SAU-NU se pozitioneaza pe "0" cand in cuvantul receptionat s-au introdus erori, indiferent de pozitia acestora.

2.2.2. Corectia erorilor

Decodorul cu corectia erorilor este format dintr-un registru de deplasare in inel de lungime n, 3 porti logice SI, un circuit de divizare cu m celule si un multiplexor. Schema bloc este prezentata in figura 3.

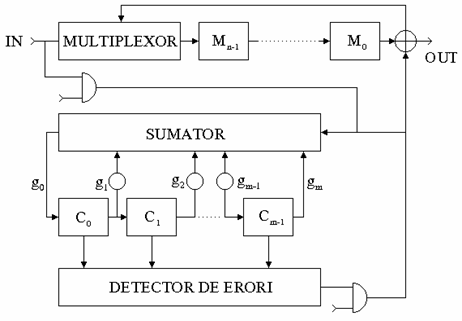
Fig. 3. Decodor cu circuit de divizare pentru corectia erorilor.

Registrul de deplasare are rolul de a inmagazina cei n biti receptionati, necesari pentru efectuarea corectiei. MUX-ul este 'deschis' pe perioada primelor n tacte si registrul se comporta ca un registru de deplasare de la stanga la dreapta. Dupa primele n tacte, celulele de divizare contin simbolurile corespunzatoare corectorului cuvantului receptionat.

Pe perioada urmatoarelor n perioade de tact se obtine cuvantul decodat astfel: bitul de iesire se calculeaza prin insumarea modulo 2 intre bitul corespunzator ca pozitie din cuvantul receptionat (bit inmagazinat in celula cea mai putin semnificativa din registru) si un bit care are valoarea "1" numai atunci cand bitul corespunzator ca pozitie din cuvantul receptionat este eronat. Deci momentul cand bitul eronat a ajuns in celula cea mai putin semnificativa din registru este identificat cu ajutorul unui detector al starii circuitului de divizare. Cand starea acestuia coincide cu ultima coloana din matricea de control H a codului, bitul de corectie devine "1", iar iesirea se obtine prin complementarea bitului eronat.

In ultimele n perioade de tact, MUX-ul permite inscrierea in celula cea mai semnificativa din registru a iesirii, deci continutul registrului este rotit de la dreapta la stanga in inel. Decodorul poate corecta o eroare indiferent de pozitia acesteia.

2.3. Codor cu registru de deplasare cu reactie

Codorul este format dintr-un registru de deplasare cu reactie cu m celule, conexiunile de reactie fiind realizate conform coeficientilor polinomului generator. Schema bloc este prezentata in figura 4.

Starea initiala a registrului este nula, astfel incat in toate celulele se afla inmagazinat simbolul "0". Pe perioada primelor k perioade de tact, comutatorul K este in pozitia "1" si se introduc simbolurile de informatie, care in acelasi timp apar si la iesire.

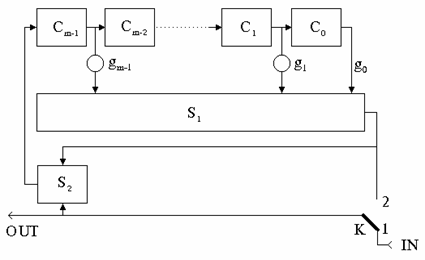
Fig. 4. Codor cu registru de deplasare cu reactie.

Comutatorul K este apoi trecut in pozitia 2, astfel incat la intrarea in registru se obtine dupa fiecare deplasare simbolul "0". Dupa m astfel de deplasari, registrul este adus in starea initiala nula. La fiecare tact registrul este evacuat, calculandu-se in continuare ultimii m biti din cuvant, bitii de control.

2.4. Decodor cu registru de deplasare cu reactie

Decodorul este format dintr-un registru de memorare, doua decodoare identice cu registre de deplasare cu reactie care functioneaza in tandem, o poarta SAU si 4 porti SI.

Schema bloc este prezentata in figura 5.

Initial comutatorul K este in pozitia 1 si in primele n perioade de tact cuvantul receptionat este pe de o parte inmagazinat in registrul de memorare, iar pe de alta parte este incarcat simultan in decodorul DC1. La sfarsitul celor n perioade de tact, decodorul DC1 contine corectorul corespunzator cuvantului receptionat.

Pe durata urmatoarelor n perioade de tact, comutatorul este trecut in pozitia 2 si iesirea se obtine insumand modulo 2 bitul din celula cea mai putin semnificativa a registrului de memorare cu un bit care va avea valoarea "1" numai atunci cand bitul corespunzator ca pozitie din cuvantul receptionat este eronat. Deci momentul in care bitul eronat a ajuns in celula cea mai putin semnificativa din registrul de memorare este identificat cu ajutorul unui detector al starii registrului de deplasare cu reactie din DC1. Cand starea acestuia coincide cu ultima coloana din matricea de control H a codului, bitul de corectie devine "1", iar iesirea se obtine prin complementarea bitului eronat.

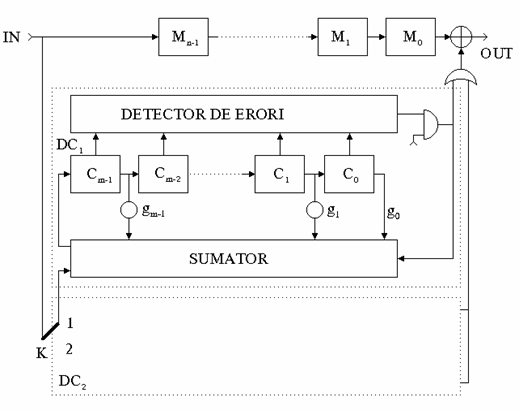
Fig. 5. Decodor cu registru de deplasare cu reactie pentru corectia erorilor.

Decodorul DC2 executa acelasi ciclu de n + n perioade de tact, dar in opozitie fata de DC1: cand DC1 calculeaza corectorul cuvantului receptionat care tocmai intra in registrul de memorare, DC2 efectueaza operatia de corectie asupra cuvantului receptionat anterior, care iese din registrul de memorare, si viceversa. In felul acesta, operatia de decodare decurge in flux continuu asupra cuvintelor receptionate de pe canal.

Decodorul poate corecta o eroare indiferent de pozitia acesteia.

3. Descrierea evolutiei programului

Programul se lanseaza in executie tastand "hamm.exe". Meniul principal prezinta urmatoarele optiuni:

C    - Codor-decodor Hamming ciclic,

T    - Teorie cod Hamming ciclic,

X    - eXit.

In optiunea C apare un submeniu in care utilizatorul alege tipul structurii fizice de implementare a schemelor codorului si decodorului:

C    - Circuite de divizare,

R    - Registre de deplasare cu reactie,

X    - eXit.

Inaintea efectuarii operatiei de codare, trebuie ales polinomul generator g(x) dintr-un set de 4 polinoame ireductibile si primitive de grad 3 si 4 (divizori ai lui , respectiv ), cu coeficienti binari:

,

,

,

.

In optiunea de codare, se introduc coeficientii binari ai polinomului simbolurilor de informatie i(x), iar apoi este descrisa secvential operatia de codare pe schema si pe tabelul evolutiei starilor, care este completat prin apasarea tastei T (Tact). Momentul in care toti bitii de informatie au fost incarcati in circuitul de codare, precum si momentul in care operatia de codare a luat sfarsit, sunt marcate prin semnale sonore. Daca in continuare se doreste efectuare operatiei de decodare, trebuie aleasa varianta de lucru:

D    - Detectia erorilor,

C    - Corectia erorilor.

De fiecare data se cere introducerea simbolurilor cuvantului eroare, care afecteaza cuvantul cu sens obtinut in urma operatiei de codare. Functionarea decodorului este prezentata pas cu pas, pe schema si/sau pe tabelul evolutiei starilor, similar optiunii de codare.

In cazul variantei cu detectia erorilor se obtine valoarea corectorului, iar in cazul variantei cu corectia erorilor se obtine cuvantul de cod refacut    la decodor.

Programul este protejat impotriva introducerii datelor nespecifice.

4. Desfasurarea lucrarii

4.1. Codarea si decodarea cu circuite de divizare.

Luand polinomul generator g(x) = 1 + x + x³ se stabilesc simbolurile de control pentru doua polinoame de informatie, notandu-se tabelul evolutiei starilor celulelor circuitului de divizare.

Se compara valorile obtinute cu rezultatele teoretice.

Se decodeaza cuvantul obtinut la punctul 4.1.1 folosind decodorul cu circuit de divizare pentru detectia erorilor. Se noteaza tabelul evolutiei starilor celulelor circuitului de divizare.

Se decodeaza cuvantul obtinut la punctul 4.1.1 folosind decodorul cu circuit de divizare pentru corectia erorilor. Se noteaza tabelul evolutiei starilor celulelor circuitului de divizare.

Se repeta punctele 4.1.3, 4.1.4 pentru o eroare, doua erori si trei erori, indiferent de pozitia acestora.

Se repeta punctele 4.1.1 - 4.1.5 pentru polinomul generator g(x) = 1 + x + x⁴.

4.2. Codarea si decodarea cu registre de deplasare cu reactie.

Luand polinomul generator g(x) = 1 + x + x³ se stabilesc simbolurile de control

pentru doua polinoame de informatie, notandu-se tabelul evolutiei starilor

celulelor registrului de deplasare cu reactie.

Se compara valorile obtinute cu rezultatele teoretice.

Se decodeaza cuvantul obtinut la punctul 4.2.1. Se noteaza tabelul evolutiei starilor celulelor registrului de deplasare cu reactie.

Se repeta punctul 4.2.3 pentru o eroare, doua erori si trei erori, indiferent de pozitia acestora.

Se repeta punctele 4.2.1, 2.2, 2.3, 2.4 pentru polinomul g(x) = 1 + x + x⁴.

5. Intrebari

5.1. Care este diferenta intre codarea realizata prin multiplicare:

v(x) = i(x)g(x)

si codarea realizata prin divizare :

5.2. Desi corectorul este

sau

de ce la decodare calcului acestuia se face numai din vectorul receptionat v'(x)?

5.3. Cand corectorul este zero?

5.4. Ce contin celulele codorului cu circuit de divizare dupa k perioade de tact?

5.5. La codorul cu circuit de divizare, de ce intrarea se face prin capatul din dreapta?

5.6. Care este numarul maxim de erori detectate de decodorul cu circuit de divizare pentru detectia erorilor?

5.7. De ce, atunci cand comutatorul K este in pozitia 2 la codorul cu registru de deplasare cu reactie, intrarea in registru este "0"?

5.8. Cand bitul de corectie generat de detectorul de erori al decodorului cu registru de deplasare cu reactie pentru corectia erorilor este "1"?

5.9. Ce se intampla daca, atunci cand programul asteapta introducerea mesajului, in loc de un simbol binar "0" sau "1", se introduce de la tastatura un caracter sau orice alta cifra?

5.10. Cum actioneaza circuitele de corectie atunci cand in cuvantul receptionat sunt doua sau mai multe erori?