Metode sistematice de rezolvare a circuitelor de curent continuu

Metode sistematice de rezolvare a circuitelor de curent continuu

Se considera o retea de curent continuu continand elemente dipolare ideale, conexa si izolata, cu l laturi si n noduri, cu o structura topologica precizata, care nu este nici incompatibila si nici cu generatoare in exces. Pentru acest circuit se presupun cunoscute valorile si sensurile tensiunilor electromotoare E_k ale tuturor surselor ideale de tensiune, valorile si sensurile injectiilor de curent I_gk ale tuturor surselor ideale de curent (fie l_g numarul acestora) precum si valorile rezistentelor R_k ale tuturor rezistoarelor.

Printr-o metoda sistematica de rezolvare a acestei retele se intelege o metoda aplicabila oricare ar fi configuratia sa topologica si oricare ar fi valorile parametrilor E_k, I_gk si R_k, si care permite determinarea celor l-l_g curenti I_j care strabat laturile care nu contin generatoare ideale de curent si a celor l_g tensiuni U_gj la bornele generatoarelor ideale de curent.

1. Metoda teoremelor lui Kirchhoff

Metoda a fost studiata in detaliu in paragraful 2.2. Adaugam doar ca in cadrul acestei metode, ca etape intermediare avand ca motivatie usurarea efortului de calcul, pot fi utilizate si teoremele de echivalenta (demonstrate cu ajutorul teoremelor lui Kirchhoff) prezentate in paragraful 2.3. Este important de retinut ca metoda lucreaza cu un numar de necunoscute egal cu numarul l al laturilor circuitului.

2. Metoda curentilor ciclici

Aceasta metoda utilizeaza un set de necunoscute primare auxiliare - curentii ciclici (care se mai numesc si curenti de ochiuri, de bucla sau de contur), care sunt niste curenti "de calcul" (fictivi), atasati cate unul pentru fiecare dintre ochiurile fundamentale ale retelei, avand proprietatea de a strabate cu o aceeasi valoare toate laturile care alcatuiesc ochiul respectiv.

In acest fel, prin superpozitie, un curent (prin oricare dintre laturile circuitului) este suma algebrica a curentilor ciclici care trec prin acea latura.

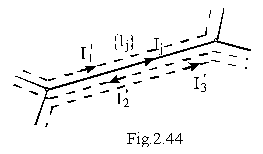
In exemplul ilustrat in figura 2.44, latura este parcursa de trei curenti ciclici, notati , si si marcati cu linie intrerupta; adoptand un sens de referinta pentru curentul I_j, acesta va avea valoarea

. (2.69)

Asadar, cunoasterea celor o=l-n+1 curenti ciclici este suficienta pentru determinarea curentilor prin toate laturile retelei.

Pentru obtinerea ecuatiilor pe care le satisfac curentii ciclici se utilizeaza teoremele lui Kirchhoff, presupunandu-se pentru inceput ca reteaua nu contine surse ideale de curent. Se remarca mai intai ca prima teorema a lui Kirchhoff este identic satisfacuta intrucat oricare curent ciclic participa in orice nod al retelei cu doua contributii egale si de semne opuse (intrand in nod printr-o latura si iesind din el prin alta latura). Apoi, generalizand relatia (2.69) sub forma

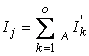, (2.70)

teorema a doua a lui Kirchhoff devine, prin alegerea sensului arbitrar de parcurgere a ochiului acelasi cu sensul de referinta al curentului ciclic:

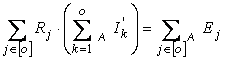(2.71)

si este de forma

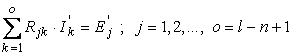. (2.72)

Scrise explicit, ecuatiile curentilor ciclici sunt:

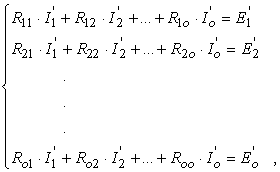
in care:

coeficientii reprezinta suma algebrica a tensiunilor electromotoare corespunzatoare surselor ideale de tensiune de pe laturile apartinand ochiului [o_j] cu numarul de ordine j (luate cu semnul plus daca sensurile sagetilor tensiunilor electromotoare coincid cu sensul ales arbitrar al curentului ciclic , respectiv cu semnul minus in caz contrar);

coeficientii R_jj reprezinta suma rezistentelor rezistoarelor de pe laturile care formeaza ochiul cu numarul j (intotdeauna R_jj>0);

coeficientii R_jk=R_kj reprezinta suma rezistentelor rezistoarelor de pe laturile comune ochiurilor avand numerele de ordine k si j, suma luata cu semnul plus sau minus dupa cum curentii ciclici si strabat acele laturi in acelasi sens sau in sensuri opuse; evident ca daca ochiurile [o_k] si [o_j] nu au laturi comune ori daca laturile comune contin doar surse ideale de tensiune, atunci R_jk = R_kj

Aceste definitii rezulta imediat prin identificare in relatiile (2.71). Pentru a ilustra acest lucru se considera circuitul din figura 2.45 in care laturile - ramuri ale arborelui ales au fost marcate cu linie ingrosata.

Inlocuind in ecuatiile (2.73) corespunzatoare teoremelor lui Kirchhoff

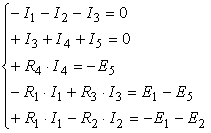(2.73)

relatiile de dependenta (2.74) intre curentii I , I , I , I , I si curentii ciclici , , care sunt

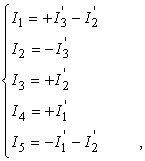(2.74)

se obtin din prima teorema a lui Kirchhoff doua identitati

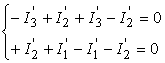
iar din cea de-a doua teorema a lui Kirchhoff, prin rearanjarea termenilor, cele trei ecuatii corespunzatoare metodei curentilor ciclici:

Expresiile coeficientilor R_jj , R_jk = R_kj si (j, k=1,2,3) confirma definitiile prezentate anterior.

In aplicarea metodei curentilor ciclici, sistemul (2.72) se scrie direct (dupa atasarea pentru fiecare ochi fundamental al retelei a cate unui curent ciclic, cu un sens de referinta ales arbitrar) si are, conform celor aratate in paragraful 2.2, solutie unica. Rezolvarea sistemului da valorile curentilor ciclici iar apoi, cu ajutorul relatiilor (2.70), se gasesc curentii care strabat laturile retelei.

Daca circuitul contine si laturi cu surse ideale de curent (fie l_g numarul acestora), se poate proceda in unul din urmatoarele doua moduri.

1. Se genereaza ochiurile fundamentale optandu-se pentru un arbore care sa nu contina laturi - ramuri cu generatoare de curent.

Prin completarea acestuia, pe rand, cu cate o coarda, incepand cu acele corzi care nu contin generatoare de curent, ultimele l_g ecuatii ale sistemului (2.72) iau formele particulare

fiecare dintre laturile cu surse de curent fiind parcursa de cate un singur curent ciclic a carui orientare este in sensul injectiei de curent I_gj. Introducand cele l_g valori cunoscute in primele o-l_g ecuatii ale sistemului (2.72), efortul de calcul scade in mod simtitor.

Mai raman de determinat cele l_g necunoscute - tensiunile la bornele generatoarelor ideale de curent care, dupa aflarea curentilor care strabat laturile cu relatiile (2.70), se gasesc fara dificultate utilizand pe contururi inchise convenabil alese teorema a doua a lui Kirchhoff.

2. Se utilizeaza teorema substitutiei, inlocuindu-se sursele ideale de curent cu surse ideale de tensiune. In acest fel apar l_g necunoscute suplimentare (tensiunile electromotoare ale noilor surse ideale de tensiune, care nu reprezinta altceva decat tensiunile la bornele generatoarelor ideale de curent substituite), dar si l_g noi ecuatii de tip (2.70) corespunzatoare laturilor cu generatoare de curent:

,

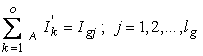oricare ar fi alegerea sistemului de ochiuri fundamentale. Si in acest caz este recomandabil sa se opteze pentru un arbore care sa nu aiba laturi - ramuri care inainte de substitutie contineau surse ideale de curent. Prin aceasta alegere, in cele l_g noi ecuatii, in locul sumelor algebrice ale curentilor ciclici va apare cate un singur termen:

daca sensul curentului ciclic coincide prin latura cu numarul de ordine j cu sensul injectiei de curent I_gj

Indiferent de procedura adoptata, se constata ca metoda curentilor ciclici este mai comoda decat metoda teoremelor lui Kirchhoff, lucrand cu un numar de necunoscute auxiliare (curentii ciclici) mai mic decat numarul de laturi ale circuitului.

Pentru exemplificare se considera circuitul din figura 2.46, a in care se cunosc valorile R , R , R , R , R , E =8 V, E =30 V, E =3 V, I_g =2 A, I_g =2 A.

1. Corespunzator arborelui marcat cu linie ingrosata pe graful din figura 2.46, b, sistemul ecuatiilor curentilor ciclici este

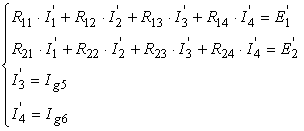
cu R =R +R R =R +R +R R =R =-R R =R , R R =-(R +R R =-R =-E =-30 V, =E +E =11 V.

Sistemul are solutia = -5 A, = 1 A, = 2 A, = 2 A si conduce la graful orientat al curentilor ilustrat in figura 2.46, c in care I == 1 A, I = -= 5A , I = -++= 3 A , I =- - = 4 A, I == 2 A, I == 2 A.

Pentru determinarea tensiunilor la bornele surselor ideale de curent se utilizeaza teorema a doua a lui Kirchhoff, fiind recomandabila alegerea unor contururi inchise care sa contina un numar cat mai mic de elemente dipolare. De exemplu:

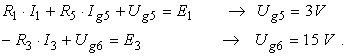
2. Pentru circuitul din figura 2.46, d (provenit din circuitul initial in care sursele ideale de curent au fost substituite cu surse ideale de tensiune), sistemul ecuatiilor curentilor ciclici, corespunzatoare optiunii pentru aceleasi ochiuri fundamentale ca si in

aplicatia precedenta, este

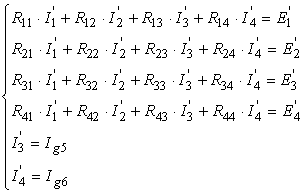
cu R =R +R , R =R +R +R , R =R +R +R , R =R R =R = -R R =R =R R =R =0, R =R = -(R +R R =R = -R , R =R =R = -E = -30 V, =E +E = 11 V,     = -E -E (-3-U_g ) V, = -E +E =(-3+U_g ) V.

Sistemul are solutia = -5 A, = 1 A, = 2 A, = 2 A, U_g = 3 V, U_g = 15 V, aceeasi cu cea obtinuta anterior.

3. Metoda potentialelor nodurilor

Si aceasta metoda utilizeaza un set de necunoscute primare auxiliare - potentialele V , V , , V_n ale celor n-1 noduri independente ale retelei, in raport cu potentialul celui de-al n-lea nod ales ca referinta (V_n

Odata cunoscute aceste potentiale, se determina tensiunile la bornele laturilor avand ca extremitati nodurile (n_k ) si (n_j ) cu relatiile

si, in continuare, in ordine, utilizand ecuatiile de functionare ale laturilor (care rezulta din ecuatiile de functionare ale elementelor dipolare de circuit si teorema a doua a lui Kirchhoff), se obtin grafurile orientate ale tensiunilor si curentilor.

Pentru determinarea ecuatiilor pe care le satisfac potentialele celor n-1 noduri independente se utilizeaza teoremele lui Kirchhoff, presupunand pentru inceput ca reteaua studiata nu are laturi care sa contina numai surse ideale de tensiune. Se remarca mai intai ca cea de-a doua teorema a lui Kirchhoff este identic satisfacuta intrucat, oricare ar fi ochiul considerat si oricare ar fi sensul sau de parcurgere, potentialul fiecarui nod participa, pentru oricare doua laturi consecutive si apartinand acelui ochi, cu doua contributii egale si de semne opuse (o data ca extremitate-sfarsit a laturii si o data ca extremitate-inceput a laturii ).