Sinteza numaratorului modulo p≠2ⁿ

Sinteza numaratorului modulo p≠2ⁿ

Numaratoarele binare prezentate anterior erau numaratoare modulo 2ⁿ obtinute prin interconectarea a ,,n'' celule binare. Caracteristica principala a acestor numaratoare este aceea ca plecand dintr-o stare initiala arbitrara acesta va evolua astfel inacat va trece prin toate cele 2ⁿ stari posibile.

De exemplu, numaratorul binar asincron direct prezentat in fig 1.1 are o evolutie care poate fi reprezentata si astfel : (vezi fig 1.10).

In cazul in care dorim realizarea unui numarator modulo p vom proceda astfel :

determinam numarul minim de cellule binare necesare pentru realizarea numaratorului cu relatia:

2ⁿ≥p    (1.2)

interconectam celulele numaratorului astfel incat din cele 2ⁿ stari posibile sa se omita 2ⁿ - p stari. Alegerea starilor omise poate fi facuta, in principiu, arbitrar. Daca insa avem in vedere faptul ca starile acestui numerator urmeaza a fi decodificate, este bines a alegem aceste stari astfel incat alegerea facuta sa conduca la o simplificare a structurii decodificatorului. In functie de starile omise pentru acelasi numar p vor exista mai multe variante de numerator modulo p.

De exemplu :- sa gasim structura unui numarator modulp cinci (p=5)

Din relatia (1.2) obtinem :

2ⁿ≥5=>n=3

ceea ce inseamna ca realizarea numaratorului modulo cinci necesita interconectarea a trei celule binare 

Numarul starilor omise va fi :

2³-5=3

O posibilitate de alegere a acestor stari este urmatoarea:omitem starile 101, 110 si 111. Evolutia acestui numerator este ilustrata in fig 1.10.

    fig.1.10 Evolutia starilor unui numerator modulo 8 si modulo 5.

In continuare facem sinteza acestui numarator modulo cinci. Pentru realizarea lui vom folosi cellule binare de tipul J - K MASTER - SLAVE pe care le interconectam intr-o schema de numarator sincron. Prin sinteza ce urmeaza a fi facuta, trebuie sa asiguram comenzile necesare pe intrarile J si K ale fiecarui bistabil astefel incat, ansamblul celor trei bistabile sa functioneze asa cum ne-am propus vezi fig 1.10.

Pentru inceput reamintim tabelul de adevar al celulei J - K master - slave, tabel pe care il rescriem sub o alta forma mai convenabila ( vezi tabelul 1.1).

Tabelul 1.1

In tabelul 1.1 sunt indicate comenzile care trebuie aplicate pe intrarile J si K pentru ca bistabilul sa treaca din starea Q_n in starea Q_n+1.

De exemplu: daca circuitul bistabil este in starea Q_n=0 si dorim ca sa ramana in aceeasi stare Q_n+1=0, atunci in mod obligatoriu pe intrarea J trebuie sa avem 0 iar pe intrarea K putem avea 0 sau 1 (pentru Q_n=0 si J=K=0 rezulta Q_n+1=Q_n=0, iar pentru J=0, K=1 rezulta Q_n+1=0). Din acest motiv am notat K=X.

Analog pot fi examinate si celelalte situatii din talelul 1.1.

Pe baza analizei functionarii celulei J - K master - slave facuta anterior putem intocmi tabelul 1.2 care ne indica evolutia numaratorului modulo p=5 impreuna cu comenzile ce trebuie aplicate pe intrarile J si K ale celor trei bistabile.

Pe baza datelor din tabelul 1.2 putem completa diagramele Karnaugh pentru comenzile J si K ale celor trei bistabile (vezi 1.11).

Tabelul 1.2

Minimizand convenabil functiile rezulta urmatoarele expresii pentru semnalele de comanda.

fig.1.11 Diagrama Karnaugh

Schema numaratorului modulo cinci este prevazuta in fig 1.12.

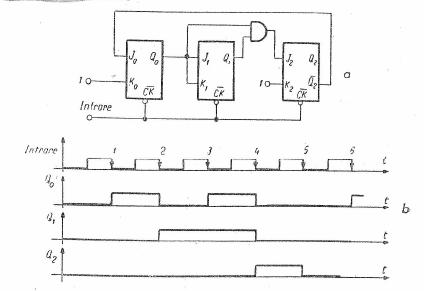
Fig 1.12 Numaratorul modulo 5 : a)schema ; b)diagrama care ilustreaza functionarea.

Problema starilor omise.

Asa cum am precizat la inceput,realizarea numaratorului modulo p presupune omiterea unui numar 2ⁿ - p stari. Se pune firesc intrebarea ce se va intampla daca dintr-un motiv oarecare (perturbatii externe) numaratorul ajunge intr-una din acele stari. Cum va evolua el ? Vom examina concret situatia numaratorului modulo cinci sintetizat anterior.

Fig 1.13 Diagrama starilor numaratorului modulo 5.

Au fost omise starile 101, 110 si 111. Daca numaratorul ajunge in starea 101 din aceasta va trece in starea 010 care face parte din ciclul principal si deci in continuare va evolua normal. Din starea 110 va trece in 001 iar din starea 111 va trece in 000 asa cum a fost ilustrat in fig 1.13.

Observam ca in cazul exemplului de mai sus, din starile omise numaratorul la primul impuls de tact reintra in ciclul principal,evoluand in continuare normal.

Intr-o serie de aplicatii acest lucru este acceptabil in altele insa nu. In plus se pot ivi si situatii (la o alta alegere a starilor omise)in care numaratorul sa nu paraseasca starea omisa sau sa treaca dintr-o stare omisa in alta,ceea ce compromite functionarea numaratorului. In astfel de cazuri se spune ca el se ,,agata'' intr-o stare oarecare(Lock-out). Pentru a evita astfel de situatii se reproiecteaza numaratorul astfel incat daca el ajunge cumva intr-o stare omisa sa aibe o evolutie convenabila.