Sisteme de cuantizare cu dither fara scadere

Sisteme de cuantizare cu dither fara scadere

Intr-un sistem de cuantizare cu dither fara scadere (Fig. 3.3(c)) iesirea cuantizorului este:

(3.63)

iar eroarea totala este data de:

(3.64)

Prezenta in eroarea totala nu numai a erorii de cuantizare, dar si a ditherului complica abordarea statistica a sistemelor de cuantizare cu dither fara scadere.

Intrarea cuantizorului este w=x+n si are fdp conditionata:

(3.65)

Deoarece x si n sunt statistic independente putem scrie:

(3.66)

Daca intrarea cuantizorului w=x+n este intre si , iesirea va fi zero (Fig. 3.1b) si In mod similar daca intrarea in cuantizor este intre si , iesirea va fi si. Deci fdp a erorii pentru o intrare fixata este:

(3.67)

Din ecutia (66) se vede ca nu poate fi facut independent de x, oricare ar fi alegerea fdp a ditherului.

Ne intereseaza atunci posibilitatea de a controla momentele erorii. Momentul conditionat de ordinul m al semnalului eroare pentru un x dat este definit astfel:

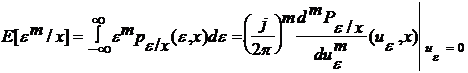(3.68)

Din relatia (3.67) rezulta transformata Fourier in raport cu e a lui si anume:

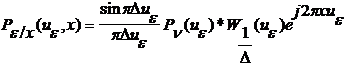(3.69)

Avand in vedere ca , rezulta relatia:

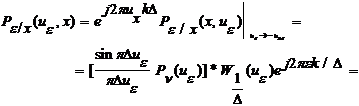
Deci:

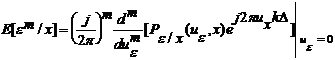(3.71)

Ne intereseaza ca sa fie independent de x. Acest lucru se intimpla daca si numai daca:

(3.72)

unde:

(3.73)

Atunci din ecuatia (3.70) rezulta:

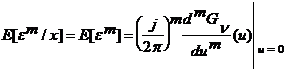(3.74)

si se obtin expresiile pentru momentele erorii totale in functie de momentele semnalului dither, prin diferentierea ecuatiei (3.73):

(3.75)

(3.76)

(3.77)

Prin diferentierea repetata a ecuatiei (72) rezulta ca este independenta functional de x pentru l=1,2,..,M daca si numai daca:

(3.78)

Relatia (3.78) este o alta forma de scriere a conditiei data de relatia (3.72).

Consideram doua valori ale erorii totale e si e care sunt separate in timp prin t si doua valori corespunzatoare ale semnalului de intrare x₁ si x₂. Folosind o relatie similara cu formula (3.67) gasim ca:

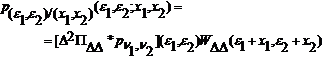(3.79)

unde convolutia este bidimensionala in raport cu e si e . In relatia (3.79) este fdp comuna a celor doua valori de dither n si n corespunzatoare intrarilor x₁ si respectiv x₂. Deci rezulta:

(3.80)

astfel incit:

(3.81)

Este clar ca nici o alegere a fc comune de dither nu va permite ca ecuatia (3.81) sa fie exprimata ca un produs de doua functii caracteristice, una numai functie de u₁, iar cealalta numai functie de u₂, pentru alegeri arbitrare ale functiei caracteristice comune de intrare. Deci e si e nu pot fi facute statistic independente pentru distributii arbitrare ale intrarii. De aceea vom investiga momentele comune ale lui e si e . pentru a realiza controlul asupra lor prin alegerea corecta a statisticii ditherului. Folosind ecuatia (3.81) putem calcula momentele comune ale lui e si e . si obtinem:

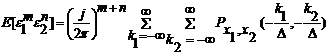
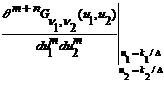
unde:

(3.83)

Daca:

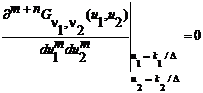(3.84)

pentru toti intregii k₁ si k₂, cu (k₁ ,k₂) (0,0), atunci:

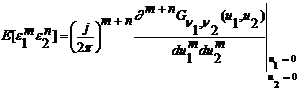(3.85)

care nu depinde de fdp comuna a intrarii. In acest caz putem scrie o expresie anloaga ecuatiei (76) care leaga momentele erorii totale cu cele ale ditherului:

(3.86)

De notat ca daca n1 si n2 sunt statistic independente si fiecare satisface ecuatia (72), atunci si sunt necorelate( si ecuatia (83) este automat satisfacuta. Mai mult, daca ditherul reprezinta un proces aleator stationar,

In particular, pentru m=n=1, folosind ecuatia (3.86), se observa ca:

(3.87)

astfel incat:

(3.88)

Astfel spectrul de putere al erorii totale este alb deoarece spectrul ditherului este alb. Acesta este cazul in cele mai multe situatii practice unde este folosit ditherul fara scadere.

Utilizind acelasi rationament folosit pentru a determina fdp conditionata a erorii totale, gasim ca fdp conditionata a erorii este data de :

(3.89)

Deci:

(3.90)

Aplicind transformata Fourier relatiei (3.89) se obtine:

(3.91)

si deci:

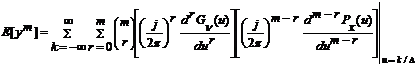(3.92)

Daca primele m derivate ale lui G_V(u) se anuleaza la toti multiplii diferiti de zero ai lui 1/D, atunci ecuatia (3.92) se reduce la:

(3.93)

unde valoarea mediei statistice a erorii totale este functie de valoarea medie statistica a ditherului, conform ecuatiei (3.77).

In mod similar, se poate obtine o expresie a momentelor comune ale valorilor de iesire y₁ si y₂, separate in timp prin t si anume:

(3.94)

unde momentele comune ale erorii totale sunt functie de cele ale ditherului conform ecuatiei (85). In particular notam ca daca aceste conditii sunt satisfacute pentru m=n=1 atunci:

(3.95)

Folosind relatia (3.86) si presupunand ca ditherul are valoare medie zero se obtine:

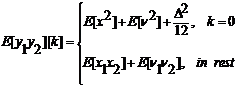(3.96)

In aceste conditii rezulta:

(3.97)

Un semnal cu dither fara scadere, generat prin sumarea a n procese aleatoare cu fdp dreptunghiulara cu medie zero, statistic independente, fiecare de amplitudine 1 LSB virf la virf da primele n momente ale erorii independente de intrarea sistemului si are ca rezultat, pentru n , o putere a erorii totale de . Intr-adevar prin adunarea a n astfel de procese aleatoare, fdp rezulta prin convolutia celor n fdp iar fc se obtine prin multiplicarea fc ale celor n procese si rezulta:

Primele n derivate ale expresiei (3.98) contin termeni cu puteri diferite de zero ale lui , care tind la zero in punctele fixate de relatia (3.73) si primele n momente ale erorii vor fi mereu independente de intrare. In plus este important de a observa ca folosind zgomote cu fdp rectangulara de amplitudine virf la virf care nu este egala cu 1 LSB (sau mai degraba nu este egala cu un numar intreg de LSB) nu vor da momente ale erorii independente de intrare, deoarece zerourile functiilor sinc asociate nu vor fi la multipli intrgi de Se poate arata ca ditherul cu fdp triunghiulara de amplitudine 2 LSB virf la virf este unic si optimal in sensul ca da momentele de ordinul 1 si 2 ale erorii totale independente de intrare, minimizind in acelasi timp momentul de ordinul 2. Altfel spus cand se foloseste un sistem de cuantizare cu dither fara scadere acest dither genereaza cresterea de zgomot cea mai mica in nivelul de zgomot efectiv fata de orice alt dither care elimina distorsiunea si modulatia de zgomot dependenta de intrare.

Ditherul potrivit de folosit este zgomotul alb sau aleator (sau pseudoaleator) avand o functie densitate de probabilitate (fdp) ce este triunghiulara cu o latime varf la varf de 2 LSB. Se numeste dither TPDF alb. Un astfel de dither este usor de generat. Teoria matematica arata ca acesta este ditherul de puterea cea mai mica ce va garanta ca exista eroare de cuantizare de medie zero (adica nu exista absolut nici-o distorsiune a semnalului corelat) si o varianta a erorii si o densitate spectrala de putere constante (adica puterea erorii totale de cuantizare este constanta si spectrul sau este alb). Nu exista ca urmare in mod absolut nici o modulatie a zgomotului dependenta de semnal. Din punct de vedere al audibilitatii sistemul digital se comporta exact ca un sistem analogic ideal, avand o rezolutie infinita sub LSB, nici o distorsiune si nici o modulatie a zgomotului.

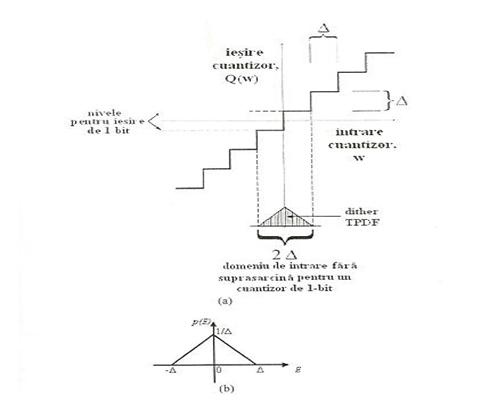
Figura 3.10.(a) Ditherul cu PDF triunghiular (TPDF) de amplitudine 2 LSB varf la varf iregistrat pe originea caracteristicii cuantizorului cu treapta la mijloc. Deși dithterul cu TPDF ocupa numai 2 LSB, acesta este domeniul de intrare complet fara suprasarcina al unui cuantizor de 1 bit. (b) Functia densitate de probabilitate pentru ditherul TPDF de amplitudine 2 LSB varf la varf.

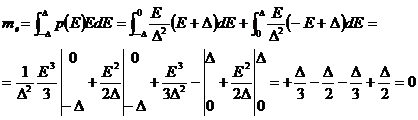(3.99)

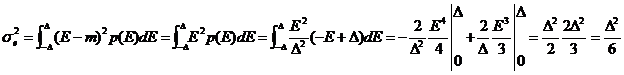
Puterea totala a zgomotului de cuantizare este egala cu si este de trei ori aceea a cuantizorului clasic fara dither.

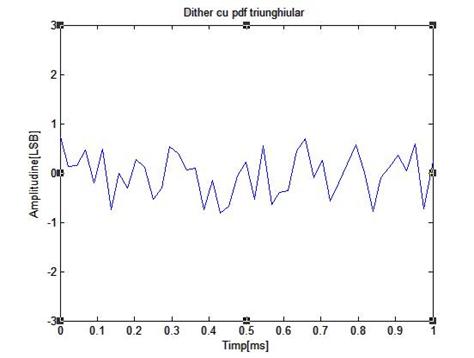
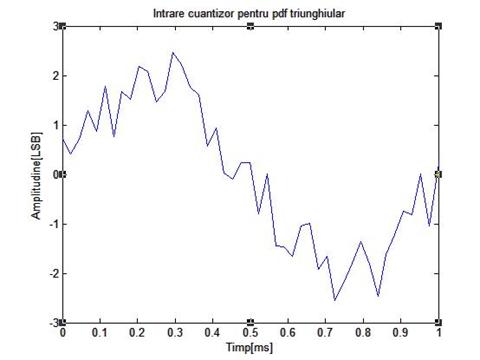
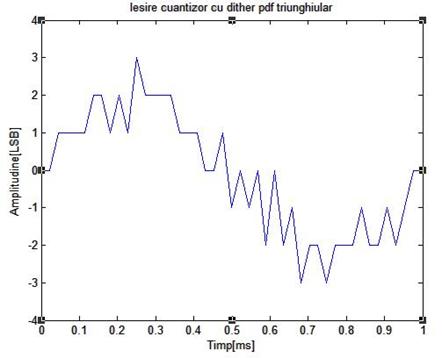
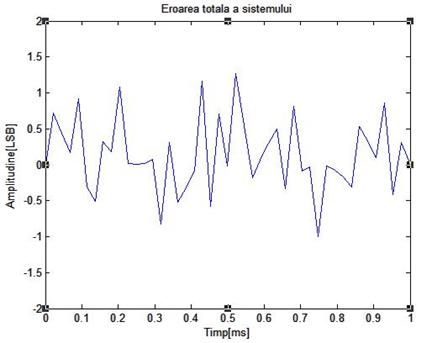
Figura de mai jos arata rezultatele unei simulari pe calculator ale unui sistem cu dither fara scadere, folosind un semnal de intrare de frecventa 1 KHz, de amplitudine 4 LSB, varf la varf. Semnalul dither folosit are amplitudinea A_d=2 LSB varf la varf si fdp triunghiulara

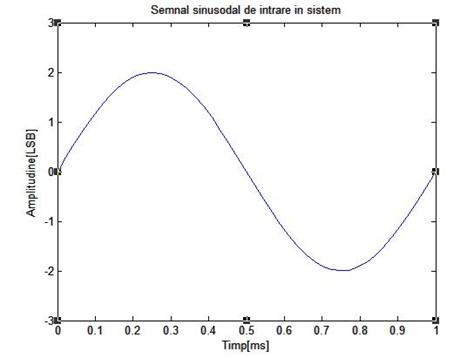
a)

b)

c)

d)

e)

f)

Figura 3.11: Rezultate obtinute prin simulare pe calculator ale cuantizarii unui semnal sinusoidal de frecventa 1 KHz si amplitudine 4 LSB varf la varf, folosind dither fara scadere

Figura 3.11 a) arata ditherul TPDF acoperind. o latime de 2 LSB pe axa orizontala a cuantizorului cu treapta la mijloc. Ditherul TPDF este in mod egal aplicabil cuantizoarelor cu treapta la mijloc sau cu pas la mijloc si este in mod egal eficient pentru amandoua.

Acest rezultat ridica imediat problema ca sistemele de 1 bit nu pot fi ditherate pozitiv deoarece figura 3.11(a) arata ca ditherul ocupa domeniul complet al intrarii fara depasire pentru cuantizorul de 1 bit (doua nivele). S-a aratat ca ditherul TPDF ocupa 2 LSB din cei 2^b LSB posedati de un sistem de b biti. Pentru sistemele multibit (b > 8), aceasta reprezinta o reducere neglijabila in domeniul dinamic. Raportul S/Z este totusi redus cu 4,77 dB (10 log3 = dB), prin triplarea efectiva a puterii zgomotului de cuantizare de la , la . Aceasta este o pierdere acceptabila intr-un sistem multibit cand se iau in considerare beneficiile. In cuantizoarele cu biti putini, aceasta ar putea fi considerat inacceptabil. Penalizarea in astfel de sisteme este ca ele nu pot total libere de distorsiuni si modulatie de zgomot. Raportul al unui sistem digital cu b biti cu dither este:

Pentru un cuantizor de 20 biti raportul este astfel 117,4 dB.

Figura 3.11 arata acelasi sinus ca in figura 3.4, de data aceasta cuantizat in mod potrivit cu pas la mijloc cu dither TPDF. Versiunea cuantizata cu TPDF a sinusului din figura 3.11(a) este aratata in figura 3.11(b). Ditherul cauzeaza semnal cuantizat care variaza doua nivele mai mult decat in figura 3.4(b). Eroarea de cuantizare cu dither TPDF (y-x) este aratata in figura 3.11(e). Ea este de . Desi in mod clar nu este independenta statistic de semnalul de intrare, este de fapt complet necorelata cu semnalul de intrare si cu el insusi.

Liniile de distorsiune corelate din figura 3.4(d) au fost schimbate cu un nivel de zgomot alb inofensiv prin cuantizarea cu dither TPDF.

O comparatie a figurii 3.4 (d) si 3.11 (f) arata de asemenea ca multe din liniile de distorsiune din figura 3.4 (b) cresc bine peste nivelul de zgomot alb din figura 3.11(f). Ultimul este de departe preferabil. Este important de a realiza ca distorsiunea a fost actualmente convertita intr-un zgomot benign. Nu este o chestiune de mascare de zgomot sau de acoperire a distorsiunii. Se adauga un semnal de zgomot dither la intrarea cuantizorului in scopul de a asigura ca, indiferent de semnalul de intrare,cuantizarea este fara distorsiuni si fara modulatie de zgomot. Teoria arata ca zgomotul alb TPDF independent este ditherul ideal.

Daca semnalul de intrare contine deja o componenta de zgomot potrivita independenta, ca zgomotul termic generat de circuitele analogice, acesta poate actiona ca dither pentru un CAD.

O cuantizarea cu dither potrivit prezerva rezolutia perfecta in timp a esantionarii

potrivite, deoarece efectul cuantizarii cu dither TPDF consta in mod simplu de a adauga

un zgomot necorelat la semnal.

Este uneori sugerat impropriu ca avand un dither cu PDF si/sau latime (adica nivelul de putere) ajustabile s-ar putea sa croim ditherul pe semnal. Dar numai ditherul TPDF de latime corecta (adica ) are aceste proprietati. Daca latimea este redusa, nu mai are distorsiuni zero si modulatie zero a zgomotului. In plus ditherul cu PDF uniform sau rectangular (RPDF) de latime , desi elimina toate distorsiunile. nu previne modulatia zgomotului si nu este recomandabil pentru audio digital de inalta calitate. Ditherul RPDF a carui latime nu este multiplu intreg de nu elimina nici distorsiunea si nici modulatia de zgomot.

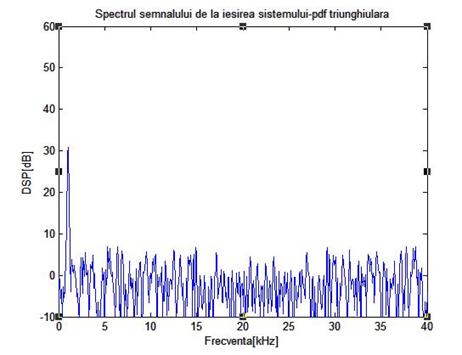
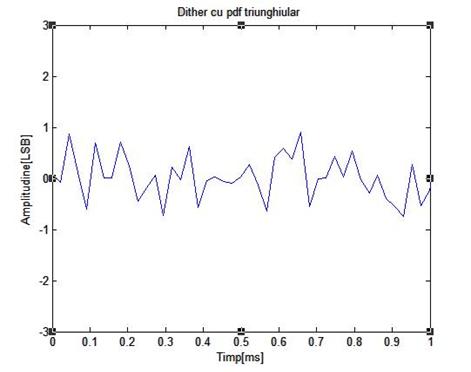
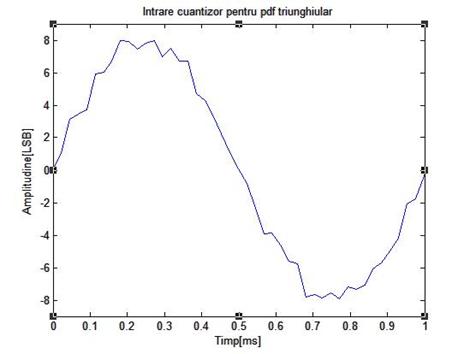
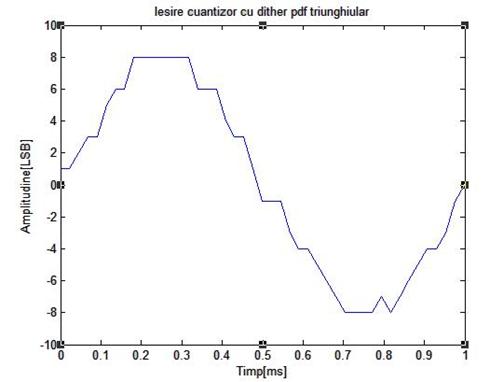
Figura de mai jos arata rezultatele unei simulari pe calculator ale unui sistem cu dither fara scadere, folosind un semnal de intrare de frecventa 1 KHz, de amplitudine 16 LSB, varf la varf. Semnalul dither folosit are amplitudinea A_d=2 LSB varf la varf si fdp triunghiulara

a)

b)

c)

d)

e)

f)

Figura 3.12: Rezultate obtinute prin simulare pe calculator ale cuantizarii unui semnal sinusoidal de frecventa 1 KHz si amplitudine 16 LSB varf la varf folosind dither fara scadere de amplitudine 1 LSB varf la varf

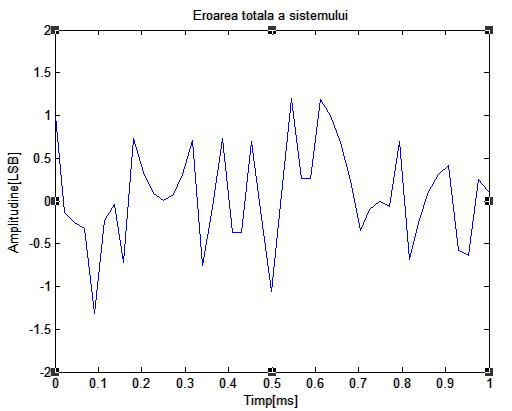
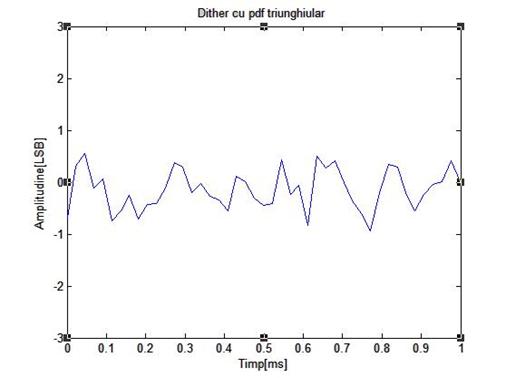
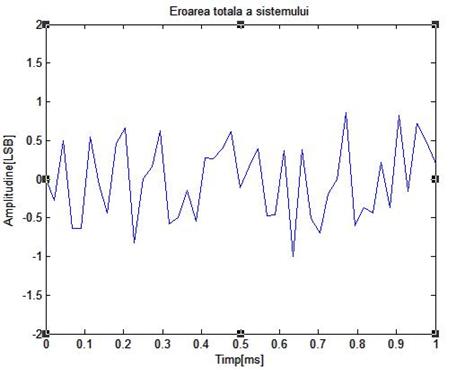
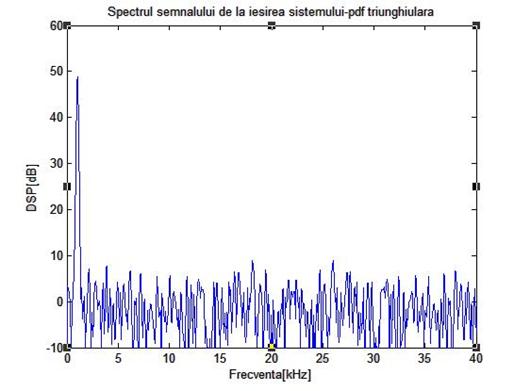
Figura de mai jos arata rezultatele unei simulari pe calculator ale unui sistem cu dither fara scadere, folosind un semnal de intrare de frecventa 1 KHz, de amplitudine 32 LSB, varf la varf. Semnalul dither folosit are amplitudinea A_d=2 LSB varf la varf si fdp triunghiulara

a)

b)

c)

d)

e)

f)

Figura 3.13: Rezultate obtinute prin simulare pe calculator ale cuantizarii unui semnal sinusoidal de frecventa 1 KHz si amplitudine 32 LSB varf la varf folosind dither fara scadere de amplitudine 1 LSB varf la varf

Se constata ca sunt vizibile vestigii ale semnalului de intrare in spectrul semnalului de iesire, indicand ca cele 2 semnale nu sunt statistic independente.Testele de ascultare au demonstrat in mod surprinzator, o independenta a erorii semnalului de iesire fata de cel de intrare.