| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Un corp este ridicat cu ajutorul unui troliu la
inaltimea h dupa legea
![]() . In timpul ridicarii corpului cablul se
infasoara pe o toba de raza r. Sa se determine timpul in care
corpul se ridica la inaltimea h ( fig.1. ) .
. In timpul ridicarii corpului cablul se
infasoara pe o toba de raza r. Sa se determine timpul in care
corpul se ridica la inaltimea h ( fig.1. ) .
|
|
R. Viteza unui punct M de pe circumferinta troliului este egala cu viteza de
ridicare
Acceleratia unghiulara a troliului este
Viteza unghiulara w devine maxima |
|
Fig.1 |
iar acceleratia unghiulara capata valoarea maxima
|
Acceleratia punctului M are componentele si modulul date de relatiile
![]() ,
,
![]() .
.
Din relatia y = h, rezulta
timpul de urcare ![]() .
.
Se considera sistemul de corpuri (fig.2).
Transmisia miscarii are loc prin intermediul unor fire inextensibile.
Cunoscand viteza ![]() si
acceleratia
si
acceleratia ![]() ale primului corp,
sa se determine vitezele si acceleratiile caracteristice ale
celorlalte corpuri.
ale primului corp,
sa se determine vitezele si acceleratiile caracteristice ale
celorlalte corpuri.
R. Miscarea de
rotatie a corpului 2 este caracterizata de viteza
unghiulara ![]() si de
acceleratia unghiulara
si de
acceleratia unghiulara![]() . Pornind de la relatiile
. Pornind de la relatiile ![]() , se obtine
, se obtine
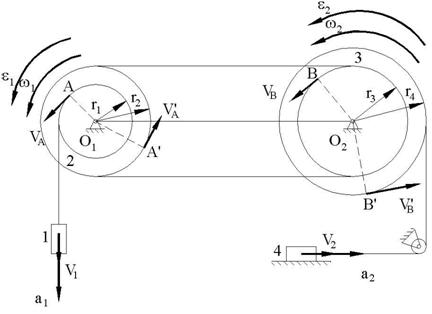
Fig.2
![]() .
.
Egaland viteza punctului ![]() cu viteza punctului B
de pe celalalt troliu, rezulta mai intai
cu viteza punctului B
de pe celalalt troliu, rezulta mai intai
![]() ,
,
iar apoi viteza unghiulara si acceleratia unghiulara a troliului 2 :
![]() .
.
Viteza si acceleratia corpului 4 vor fi :
![]()
![]() .
.
Cunoscand spatiul parcurs de primul corp x1, se pot calcula
deplasarile celorlalte corpuri ![]() .
.
Un disc de raza r, avand viteza initiala ![]() , este franat si executa o miscare de
rotatie uniform incetinita. Cunoscand acceleratia
miscarii
, este franat si executa o miscare de
rotatie uniform incetinita. Cunoscand acceleratia
miscarii ![]() , sa se calculeze numarul de rotatii pana
la oprire, timpul de miscare al discului si viteza unghiulara la
jumatatea intervalului de timp (fig.3).
, sa se calculeze numarul de rotatii pana
la oprire, timpul de miscare al discului si viteza unghiulara la
jumatatea intervalului de timp (fig.3).
R. Notand cu q unghiul descris de raza discului, ecuatia diferentiala a miscarii este
![]() , din care se deduce prin integrare
, din care se deduce prin integrare
![]() ,
, ![]() .
.
|
|
Punand conditiile initiale ale miscarii se calculeaza constantele de integrare Ecuatiile miscarii discului, devin In momentul opririi discului
viteza unghiulara se anuleaza |
|
Fig.3 |
Unghiul total descris si numarul de rotatii pana la oprire sunt
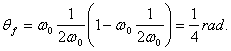 ,
, ![]() .
.
Viteza unghiulara ![]() a discului la mijlocul
intervalului de timp
a discului la mijlocul
intervalului de timp ![]() este jumatate din
viteza unghiulara initiala
este jumatate din
viteza unghiulara initiala
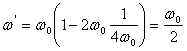
In acest moment se calculeaza viteza si acceleratia unui punct de pe periferia discului
![]() .
.
. Un solid aflat in miscare elicoidala
are vectorii caracteristici ![]() si
si ![]() cunoscuti.
Sa se arate ca locul geometric al punctelor de viteza egala
cu kv0 este un cilindru,
in care k este o constanta
supraunitara (fig.4).
cunoscuti.
Sa se arate ca locul geometric al punctelor de viteza egala
cu kv0 este un cilindru,
in care k este o constanta
supraunitara (fig.4).
R Viteza unui punct M al solidului se calculeaza cu formula
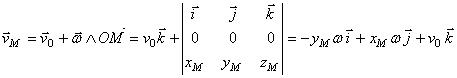
|
|
de unde se deduce rezulta ecuatia care reprezinta un cilindru de raza |
|
Fig.4 |
a) Daca k = 1, locul geometric al punctelor de viteza v0 este axa de rototranslatie.
b) Pentru k > 1 exista un singur cilindru al punctelor solidului pentru care vitezele sunt egale cu kv0.
Un disc de raza r se roteste in
jurul axei sale dupa legea![]() . Sa se determine viteza si acceleratia unui
punct de pe circumferinta.
. Sa se determine viteza si acceleratia unui
punct de pe circumferinta.
R. Viteza punctului
este ![]() . Componentele acceleratiei punctului sunt:
. Componentele acceleratiei punctului sunt:
![]() ,
, ![]() ,
,
de unde se obtine ![]() .
.
Cazuri particulare :
t ![]()
![]() ,
,
t =1 s ![]()
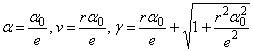
![]()
![]()
![]() .
. ![]() . Punctul tinde asimptotic spre starea de repaus, deoarece
. Punctul tinde asimptotic spre starea de repaus, deoarece ![]() .
.
Se cunosc vitezele a doua puncte A, B:![]() si intensitatea
si intensitatea ![]() a vitezei unui alt
punct C ale unui paralelipiped de
laturi
a vitezei unui alt
punct C ale unui paralelipiped de
laturi ![]() . Sa se determine viteza unghiulara
. Sa se determine viteza unghiulara ![]() si axa instantanee
a miscarii elicoidale (fig. 6).
si axa instantanee
a miscarii elicoidale (fig. 6).
R. Fie ![]() proiectiile
vectorului
proiectiile
vectorului![]() pe axele Oxyz ale
paralelipipedul.
pe axele Oxyz ale
paralelipipedul.
Intre vitezele celor doua puncte A
si B exista relatia ![]() , care devine
, care devine
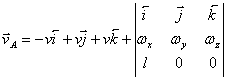 =
= ![]() .
.
Procedand asemanator se poate calcula viteza punctului C:
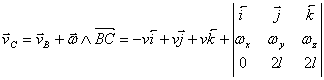 =
=
= ![]() .
.
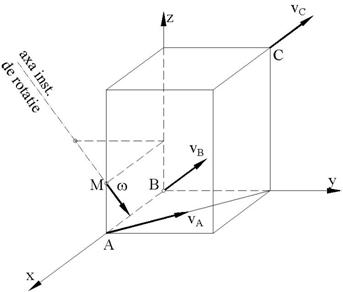
Fig. 6
Din expresiile analitice
![]() ,
, ![]() ,
,
rezulta ecuatiile
![]() ,
,
![]() .
.
Rezolvand acest sistem de ecuatii, deducem cele patru necunoscute
![]() ,
,
care pot defini
vectorul viteza unghiulara: ![]() . Ecuatiile axei instantanee a miscarii
elicoidale
. Ecuatiile axei instantanee a miscarii
elicoidale
![]()
devin ![]() .
.
Viteza unui punct oarecare M de pe axa instantanee a miscarii elicoidale este data de relatia
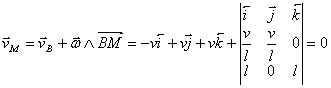 .
.
Acelasi rezultat, se obtine daca se calculeaza viteza minima
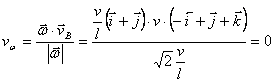
Deoarece ![]() , iar
, iar ![]() , rezulta ca paralelipipedul are o distributie
de viteza caracteristica unei miscari instantanee de
rotatie.
, rezulta ca paralelipipedul are o distributie
de viteza caracteristica unei miscari instantanee de
rotatie.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1193
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved