Controlul vitezei prin orientarea de camp

Controlul vitezei prin orientarea de camp

La o masina de curent continuu de obicei axa indusului si infasurarea excitatiei sunt perpendiculare una pe cealalta. Tensiunile magnetomotoare stabilite de curenti in aceste infasurari vor fi deasemenea perpendiculare. Daca se neglijeaza saturatia miezului, campurile perpendiculare nu produc efect de interactiune unul asupra altuia.

Cuplul dezvoltat poate fi exprimat ca:

Tem= K_a N.m ( 1.14.)

unde K_a e o constanta, f (I_f) fluxul de excitatie iar I_a curentul armaturii

( indusului). Aici unghiul cupului este de 90⁰ si evident fluxul poate fi controlat independent de flux modificand curentul I_a.

Deoarece constanta de timp a circuitului indusului e de obicei mult mai mic decat cel al infasurarii de excitatie, controlul cuplului prin modificarea curentului armaturii e mai rapid decat modificarea curentului I_f sau o modificare a ambilor curenti.

In general controlul cuplului unei masini asincrone trifazate nu este atat de direct ca al unei masini de curent continuu din cauza interactiunilor dintre campurile statorului si rotorului a caror orientare nu este tinuta la 90⁰ (spatial) ci variaza functie de conditiile de lucru.

Campul infasurarii rotorului la o masina asincrona poate fi asemanator cu cel al campului infasurarii la o masna de curent continuu, dar acesta fiind indus nu este controlabil independent.

Cu excitatie sinusoidala, campul rotorului se roteste la o viteza sincrona. Daca ar trebui sa selectam un cadran de rotatie sincrona qdo a carei axe sa fie aliniate cu campul rotorului si componeneta q a campului rotorului l _qr in sistemul de referinta ales ar fi 0, adica:

Wb (1.15)

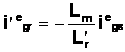A (1.16)

cu , prima ecuatie se reduce la inecuatia din 1.14. la :

T_em= Nm (1.17)

Inlocuind folosind (1.16) atunci (1.170 poate fi scris in forma dorita si mai simpla:

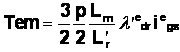Nm (1.18)

Aceasta ecuatie arata ca fluxul de inductie al rotorului nu este deranjat, cuplul poate fi controlat independent regland (modificand) componenta q de curent a statorului .

Ca sa ramana neschimbat la 0, p trebuie sa fie 0, si in acest caz ecuatia axelor q de tensiune ale infasurarilor rotorului fara tensiuni aplicate la rotor vor deveni:

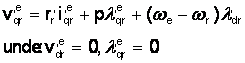V (1.19)

Cu alte cuvinte viteza de alunecare trebuie sa satisfaca relatia:

w_e w_r = - rad/s electrici (1.20)

Deasemenea, daca l^'e_dr trebuie sa ramana neschimbat, p . l^'e_dr trebuie sa fie 0.

Folosind aceasta conditie si cea de l^'e_qr= 0 in ecuatiile de tensiune pe axa d a rotorului, vom obtine conditia ca i^'e_dr sa fie 0, adica

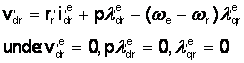V (1.21)

si cu i^'e_dr = 0, X^'e_dr = L_mi^e_ds

Substituind aceasta in 1.20 si folosind ecuatia 1.16 vom obtine urmatoarea relatie dintre viteza de alunecare si raportul dintre componentele curentului de stator qd pentru ca axa d a planului de axe de rotatie sincrona sa fie aliniata la campul rotorului.

w_e w_r = srad/s electricit (1.22)

In practica marimea fluxului rotorului poate fi schimbata prin controlul lui i ^e_ds iar orientarea axei d a campului rotorului poate fi mentinuta pastrand fie viteza de alunecae, fie i^e_qs in concordanta cu ecuatiile 1.22.

Cu o orientare corecta a campului dinamica lui l^'e_dr va fi incredintata axei d si e determinata la constanta de timp a circuitului rotoric .

Aceasta situatie se poate vedea din (1.21) cu i^'e_dr inlocuind pe

l^'e_dr - L_mi^'e_ds / L_r^') adica:

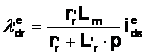sWbt rotitori (1.23)

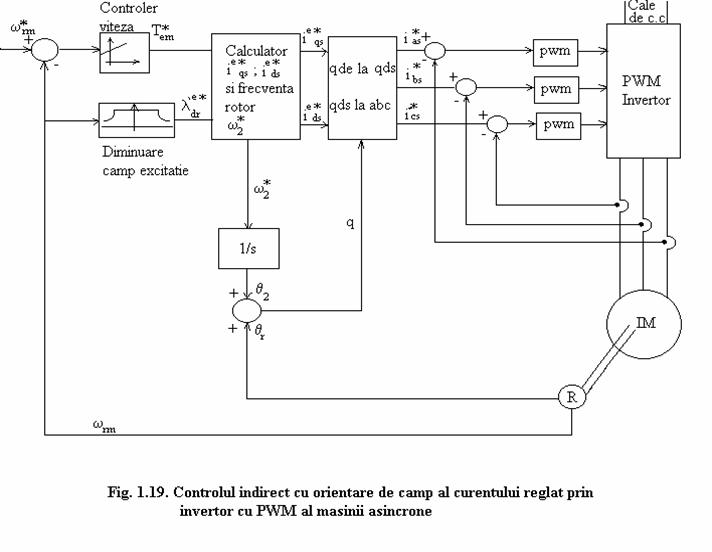
Schemele de reglare cu camp orientat pentru motoare asincrone se refera la tipul direct cand unghiul aratat in figura 1.16 si e determinat direct cum ar fi in cazul masuratorii directe a fluxului in intrefier, sau la tipul indirect cand unghiul rotorului e determinat prin masurari indirecte

cum ar fi viteza de alunecare.

Controlul direct al curentului cu camp orientat

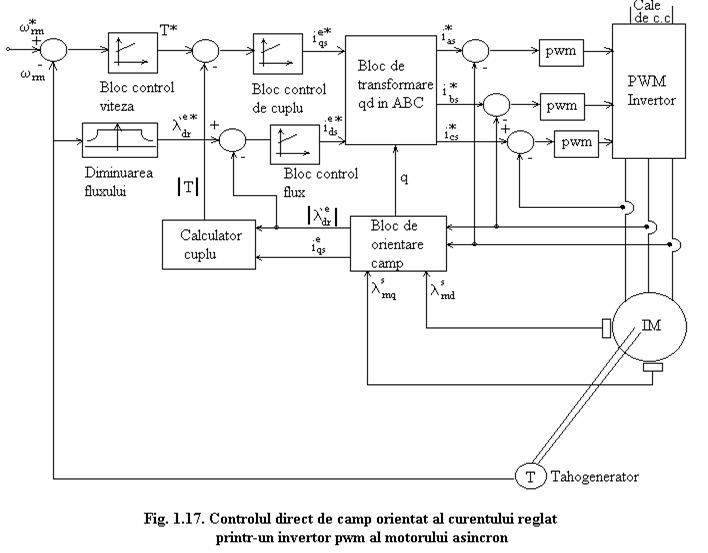
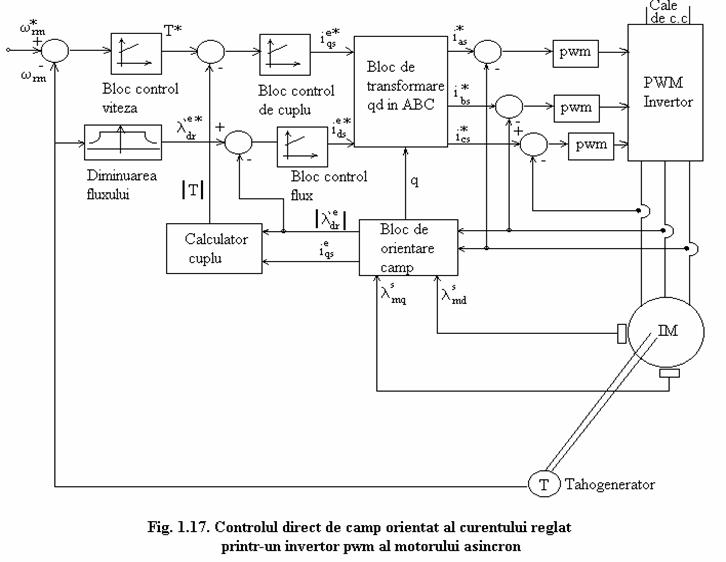
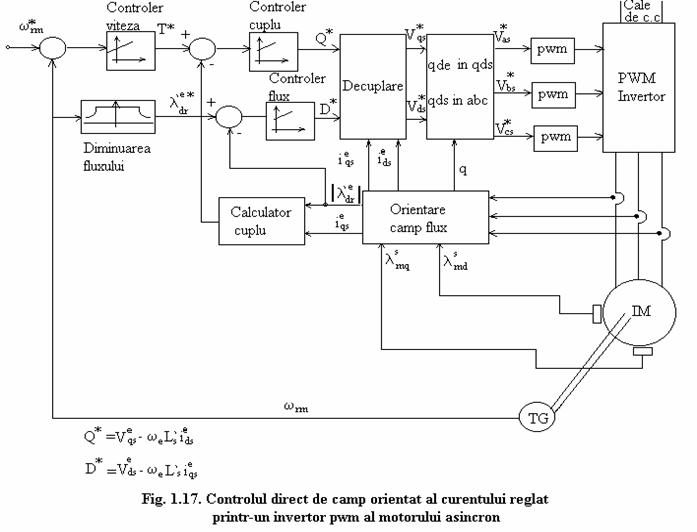
In fig.1.17 e reprezentata o schema care realizeaza controlul cu orientare de camp directa pentru controlul cuplului folosind un invertor cu regulator de curent pwn. Pentru orientarea campului comanda curentului din stator e mai directa decat controlul tensiunii statorului, cea de a doua abordare trebuie sa permita inductante tranzitorii ale startorului ca efecte secundare.

Cu o tensiune de curent continuu adecvata si cu dispozitive de comutatie rapida, controlul direct al curentului de stator poate fi realizat cu usurinta.

Metoda directa se bazeaza pe detectarea fluxului in intrefier folosind bobina de explorare potrivite speciale sau dispozitive cu efect Hall.

Curgerea in intregrator asociate cu bobina de explorare este problematica in mod special la frecvente joase. De asemenea dispozitivele Hall sunt sensibile la temperatura si totodata foarte fragile.

Fluxul masurat in intrefier este rezultanta sau fluxul mutual. Nu e acelasi cu fluxul de inductie din infasurarea rotorului a carui unghi r este unghiul dorit pentru orintarea campului dar asa cum se arata mai jos asociat cu curentul din stator masurat, putem determina valoarea lui r si marimea fluxului rotorului. Curentii statorului a, b, c sunt masurati si transformati mai intai in curenti qd stationari folosind:

A (1.24)

Adaugand si scazand un termen in partea dreapta, fluxul de inductie al statorului pe axa q in cadrul de referinta stationar poate fi exprimat ca:

Wb rotitor

Intrucat este egal cu , putem determina din conditiile masurate adica:

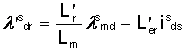(1.26)

Analog, poate fi determinat din:

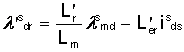Wb rotitor (1.27)

Folosind si calculat din (1.26) si (1.27) putem determina cos si sin de q prin urmatoarele relatii din figura (1.16)

sin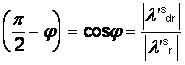

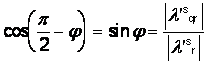(1.28)

unde:    (1.29)

Calculele de mai sus (1.24) la (1.29) sunt realizate in blocul de orientare a campului dat in mijlocul figurii 1.17.

Valoarea calculata a lui este trimisa inapoi la intrarea controlorului de flux ce regleaza fluxul in intrefier. In interiorul blocului de calcul al cuplului, valorile calculate ale lui si sunt folosite in 1.18 pentru a estima valoarea cuplului dezvoltat de masina, iar cuplul estimat este retransmis la intrarea comenzii de cuplu.

Iesirile respective ale cuplului si controlorilor de flux sunt valorile de comanda, si din cadrul de referinta de camp orientat al rotorului.

In cadrul blocului de transformare de la qd la abc sunt urmatoarele transformari de la qde la qds pana la a,b,c.

A (1.30)

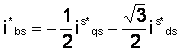
A (1.31)

Controlul direct al tensiunii cu camp orientat

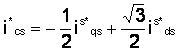
Orientarea campului curentilor statorului poate fi deasemenea realizata prin aplicarea tensiunilor statorului corespunzatoare. Deoarece strategia intr-o schema de camp orientat este de a evita perturbarea fluxului de inductie al rotorului pe cat e posibil cand raspunde la o schimbare de cuplu de sarcina, putem folosi un model tranzitoriu descris in legatura cu curentii statorici qd corect orientati si sa se determine tensiunile statorice aplicate.

Curentii de stator qd sunt determinati transformand curentii masurati a,b,c in qd stationari folosind 1.24 si valoarea lui q, determinata prin 1.28 ca mai jos:

A (1.32)

A

Intr-un model tranzitoriu se stie ca pentru o situatie in care fluxurile de inductie ale rotorului se pot presupune, constante, masina poate fi reprezentata prin tensiuni constante in urma inductiei tranzitorii a statorului.

Raspunsul masinii la tranzitiile partii de stator poate fi reprezentat printr-un set de ecuatii date de ;

Fluxul de inductie al statorului poate fi exprimat in termeni doar de curentii din stator si flux de inductie rotor, adica:

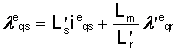
Wb rotitor

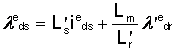(1.33)

Inlocuind expresiile de mai sus pentru fluxul de inductie al statorului in termenul din stanga al ecuatiilor:

vom obtine:

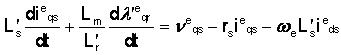V (1.34)

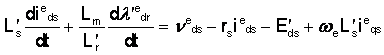V

Fixand termenii derivativi de timp ai fluxurilor rotorici la 0 si rearanjand astfel ca partea stanga sa cuprinda suma tensiunii din urma impedantei tranzitorii si a caderii de tensiune de-a lungul impedantei tranzitorii a statorului obtinem:

(1.35)

Figura 1.18 arata o schema directa cu orientare de camp folosind un regulator de tensiune a statorului.

In aceasta schema, cele doua valori din stanga din ecuatiile 1.35 se presupune ca sunt produse de controlorii de flux si de cuplu.

Regland acste iesiri de controleri ca termeni de curent de cuplare in cruce ale parti drepte ai ecuatiilor 1.35 vom obtine valorile de comanda dorite pentru si . Valorile de comanda pentru tensiunile statorice a bc pot fi calculate astfel:

V (1.36)

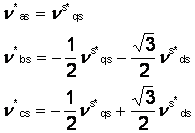
(1.37)