ARBORI BINARI. DEFINITIE SI TERMINOLOGIE

ARBORI   BINARI. DEFINITIE SI TERMINOLOGIE

Definitie. Se numeste arborescenta un arbore caracterizat astfel:

are un varf special numit radacina

celelalte noduri pot fi grupate in p>0 multimi disjuncte,
V,,V₂,,V_p, astfel incat fiecare din aceste multimi sa contina un nod adiacent cu radacina iar subgrafurile generate de aceasta sa fie la randul lor arborescente.

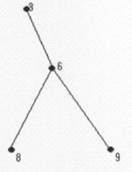
Exemplu. Graful din figura de mai jos este o arborescenta.

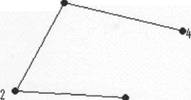
Demonstratie:

Graful este arbore. Contine un nod special numit radacina, fie acesta nodul 1.

Celelalte noduri se pot imparti in multimi disuncte V₁= si V₂= astfel incat in multimea V₁, sa existe nodul 2 adiacent cu radacina, iar in multimea V₂ sa existe nodul 4 adiacent cu radacina, si subgrafurile generate de V, si V₂ sa fie la randul lor arborescente.

Obsevatii: 1. Daca o arborescenta este formata dintr-un singur nod spunem ca este formata doar din nodul radacina.

Daca ordinea relativa a arborescentelor, generate de V₁,V₂,,V_p din

definitie, are importanta, arborescenta se numeste arbore ordonat.

In reprezentarea grafica a unei arborescente, nodurile se deseneaza pe nivele, astfel:

pe primul nivel  : se deseneaza radacina;

pe al doilea nivel : se deseneaza nodurile adiacente cu radacina;

pe al treilea nivel : se deseneaza nodurile adiacente cu noduri de pe

nivelul al doilea, si nu se afla pe nivelul 1;

pe al k-lea nivel : se deseneaza nodurile adiacente cu noduri de pe nivelul k-1, si nu se afla pe nivelul k-2;

Exemplu de arborescenta reprezentata grafic, conform regulii prezentate mai sus:

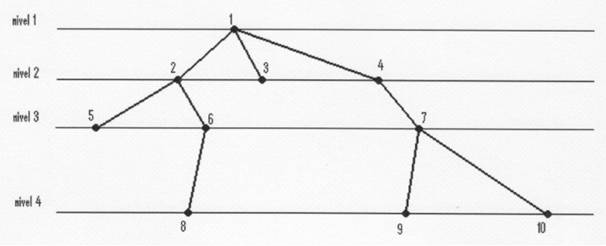
Definitie. Se numeste arbore binar, o multime finita de noduri care este vida, fie un arbore ordonat in care fiecare nod are cel mult doi descendenti(succesori).

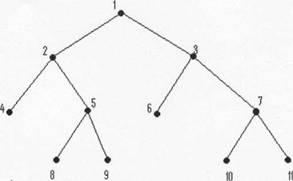
Exemplu de arbore binar:

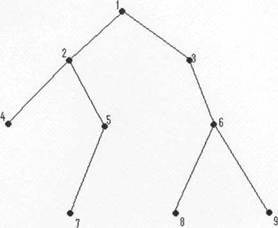
Teoriile care trateaza arborii folosesc in plus fata de cei care se refera la structurile arborescente in general, urmatoarele notiuni:

succesor stang: pentru un nod, se numeste succesor stang acel successor care este figurat in stanga sa.

Exemplu: pentru nodul 1, succesorul stang este nodul 2;

pentru nodul 5, succesorul stang este nodul 7;

pentru nodul 7, succesorul stang nu exista.

succesor drept: pentru un nod, se numeste succesor stang acel succesor

care este figurat in stanga sa.

Exemplu: pentru nodul 1, succesorul drept este nodul 3; pentru nodul 5, succesorul drept nu exista;

subarbore stang: pentru un nod se numeste subarbore stang subarborele care se obtine suprimand muchia care-1 leaga pe acesta de succesorul sau stang; daca succesorul stang nu exista, se spune ca subarborele stang este vid. Exemplu. Pentru nodul 1 subarborele stang este:

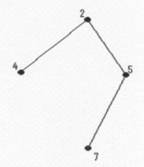
subarborele drept: pentru un nod, se numeste subarbore drept subarborele care

se obtine suprimand muchia care-1 leaga pe acesta de succesorul sau drept; daca succesorul drept nu exista, se spune ca subarborele drept este vid. Exemplu. Pentru nodul 1 subarborele drept este:

- nod frunza (sau terminal): un nod se numeste frunza daca nu are descendenti.

Exemplu. In arborele prezentat mai sus, frunzele sunt nodurile 4,7,8 si 9.

Definitie. Se numeste arbore binar complet un arbore binar in care fiecare nod, care nu este frunza, are exact doi descendenti.

Exemplu de arbore binar complet:

Propozitie: Un arbore binar complet care are p noduri terminate, situate pe acelasi nivel, are in total 2p-l noduri.

Exemplu: Fie arborele binar complet din figura:

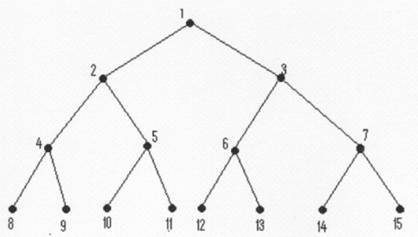
Deoarece are p=8 noduri terminale, toate situate pe acelai nivel, are, conform propozitiei de mai sus, 2p-1=2*8-1=15 noduri.