UNIVERSITATEA POLITEHNICA BUCURESTI

FACULTATEA DE AUTOMATICA SI CALCULATOARE

Proiect ASDN

Algoritmul de minimizare Karnaugh

CUPRINS:

Tema proiectului.pag.3

Prezentarea algoritmuluipag.3

Tabela Karnaughpag.3

Minimizare Karnaugh.pag.5

Implementarea algoritmuluipag.7

Explicarea programului in C++.pag.7

Listarea codului sursa.pag.11

Tema Proiectului :

Tema proiectului consta in implementarea metodei Karnaugh de minimizare a functiilor booleene printr-un algoritm de calcul in limbajul Borland C++.

1.Prezentarea algoritmului

Tabela Karnaugh

Sa presupunem ca este data o functie (in functie de mintermi). Se cauta mintermul cel mai mare si se reprezinta in binar. Se va observa numarul minim de biti care ne trebuie pentru a reprezenta acel minterm in binar. Apoi se vor reprezenta toti mintermii in binar, pe numarul minim de biti calculat anterior. Se alcatuiste diagrama Karnaugh (cu ajutorul codului Grey).

Codul Grey se alcatuieste pornind de la 0 reprezentat in binar pe cati biti sunt. Numarul de variabile reprezinta numarul de biti necesari (bitul poate lua valorile 0 si 1). Apoi se variaza cate un bit pornind de la bitul cel mai putin semnificativ (deplasare spre stanga). De exemplu:

pentru 1 variabila avem: 0 si 1 (sunt 2¹ de combonatii),

pentru 2 variabile avem: 00, 01, 11 si 10 (sunt 2² de combonatii),

pentru 3 variabile avem: 000, 001, 011, 010, 110, 111, 101 si 100 (sunt 2³ de combonatii),

pentru 4 variabile avem: 0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001 si 1000 (sunt 2⁴ de combonatii),

pentru 5 variabile avem: 00000, 00001, 00011, 00010, 00110, 00111, 00101, 00100, 01100, 01101, 01111, 01110, 01010, 01011, 01001, 01000, 11000, 11001, 11011, 11010, 11110, 11111, 11101, 11100, 10100, 10101, 10111, 10110, 10010, 10011, 10001, si 10000 (sunt 2⁵ de combonatii).

Pentru tabela Karnaugh se imparte numarul de variabile in doua (fix in jumatate). Se alcatuieste tabela in care pe coloana sunt trecuti bitii cei mai semnificativi (de la stanga - cel mai semnificativ la dreapta), iar pe linie bitii cei mai putin semnificativi (tot de la stanga la dreapta - cel mai putin semnificativ). Daca este numar impar de variabile vom avea mai multe variabile pe coloana (numar variabile+1)/2. Variabilele sunt notate cu "x_indice", unde indicele reprezinta 2^{numarul bitului respectiv}. In tabela Karnaugh se pune 1 pe pozitia corespunzatoare coloanei bitilor celor mai semnificativi si liniei bitilor celor mai putin semnificativi din codul binar al mintermului respectiv.

Tabela Karnaugh se alcatuieste numai din 1 si 0 (0 acolo unde nu este minterm).

Exemplu 1 (numar par de variabile):

Persupunem functia f = m₀ + m₂ + m₄ + m₈ + m₁₀ + m₁₂. Numarul minim de variabile este 4, deoarece 12 in binar este 0.01100, adica doar ultimii 4 biti sunt importanti. Deci variabilele vor fi x₁, x₂, x₄, x₈.

Trecerea in binar:

Tabela Karnaugh:

Exemplu 2 (numar impar de variabile):

Avem: f = m₀ + m₃ + m₅ + m₇ + m₈ + m₁₁ + m₁₃ + m₁₅ + m₂₀ + m₂₁ + m₂₂ + m₂₃ + m₂₈ + m₂₉ + m₃₀ + m₃₁. Numarul minim de variabile este 5: x₁, x₂, x₄, x₈, x₁₆.

Trecerea in binar:

Tabela Karnaugh:

Minimizare Karnaugh

Minimizarea inseamna, defapt, gruparea mintermilor. Se foloseste principiul "x+x'=1".

Daca un minterm este "vecin" cu un alt minterm atunci ei se pot minimiza ,si, deci dispare o variabila, acea variabila care apare direct si negat. "Vecin" inseamna un minterm care variaza de alt minterm printr-o singura variabila.

Pentru proiect avem maxim 10 variabile, deci minimizarile pot fi urmatoarele:

daca grupam 2 mintermi va disparea 1 variabile,

daca grupam 4 mintermi vor disparea 2 variabile,

daca grupam 8 mintermi vor disparea 3 variabile,

daca grupam 16 mintermi vor disparea 4 variabile,

daca grupam 32 mintermi vor disparea 5 variabile,

daca grupam 64 mintermi vor disparea 6 variabile,

daca grupam 128 mintermi vor disparea 7 variabile,

daca grupam 256 mintermi vor disparea 8 variabile,

daca grupam 512 mintermi vor disparea 9 variabile,

daca grupam 1024 mintermii (adica toto posibili) functia va fi 1: f=1.

Minimizarile se fac pentru ca vom avea la implementarea circuitului mai putine intrari si deci costul va fi mai mic.

Exemplul 1:

Tabela Karnaugh:

Alegem mintermul m₀ (0000 in binar) si se observa ca este "vecin" si cu m₄ (0100 in binar) si cu m₂ (0010 in binar) si cu m₈ (1000 in binar). Alegem pentru minimizare mintermul m₄. m₀ reprezentat in functie de variabile este x₈'x₄'x₂'x₁', iar m₄ este x₈'x₄x₂'x₁'. Dupa minimizare vom avea x₈'x₂'x₁' (dispare variabila x₄). Se observa ca se pot minimiza si mintermii m₈ cu m₁₂ care difera tot prin aceeasi variabila. Dupa minimizare vom avea x₈x₂'x₁'. Acum se pot minimiza m_0,4 cu m_8,12 si rezulta minimizarea x₂'x₁'. Mai departe nu se mai poate merge doarece nu mai exista nici o minimizare la fel de mare care sa fie adiacenta cu minimizarea gasita.

Ne uitam acum la mintermii ramasi! Luam primul minterm gasit neacoperit. Gasim mintermul m₂. Acesta este "vecin" cu m₀ si cu m₁₀. Il minimizam cu m₁₀, deoarece m₀ a fost deja acoperit. Vom avea minimizarea x₄'x₂x₁', dispare variabila x₈. Acum se pot minimiza m_2,10 cu m_0,8 si rezulta minimizarea x₄'x₁'. Mai departe nu se mai poate merge doarece nu mai exista nici o minimizare la fel de mare care sa fie adiacenta cu minimizarea gasita.

2.Implementarea algoritmului

2.1. Explicarea programului in C++

Structuri:

Programul C foloseste doua structuri:

prima, "Acoperire", este o lista simplu inlantuita (defapt este prima celula dintr-o lista simplu inlantuita) si este folosita in a doua structura:

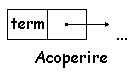
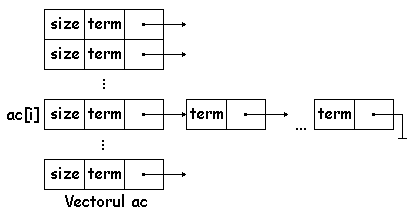
a doua, "Acoperiri", este un vector si fiecare element din vector contine o lista simplu inlantuita, prima structura , plus un intreg in care se retine marimea acoperirii curente. Deci in structura "Acoperire" se retine o singura acoperire, iar intr-un vector de "Acoperiri" se retin toate acoperirile si marimea lor:

Alocare de memorie:

Vectorul de tipul "Acoperiri" este alocat static, iar lista simplu inlantuita este alocata dinamic pe parcurs, de fiecare data cand se introduce un minterm in minimizarea curenta (in lista curenta). Se aloca memorie pentru o singura celula. In program nu se face eliberare de memorie!

Variabilele globale:

Acestea sunt:

unsigned char tabela [32][32],

int nrvar, terms,

int k,

int vvar,

int ovar,

int mask,

Acoperiri ac [512];

Unde "tabela" este o matrice in care se retin toti mintermii. Este alocata static si fiind o variabila globala este initializata cu zero. Tabela va fi formata din 0 si 1, 1 acolo unde se afla un minterm. Dimensiune este de 32, deoarece 32 reprzinta 2⁵ (pe coloane avem maxim 5 variabile, la fel si pe linii). Fiecare element din matrice este reprezentat pe 8 biti. "nrvar" reprezinta numarul de variabile. Acesta trebuie dat de utilizator sau specificat in fisierul de intrare si nu este calculat de catre program fiindca minterminii sunt trecuti direct in tabela si nu se retin in nici o structura (mai putina memorie alocata). "terms" reprezinta numarul mintermilor functiei data de catre utilizator. "k" reprezinta numarul de acoperiri (minimizari), "vvar" este numarul de variabile de selectie de aseazate in tabela pe verticala, iar 2^vvar reprezinta numarul de linii din tabela. "ovar" este numarul de variabile de selectie de pe tabela asezate pe orizontala, iar 2^ovar reprezinta numarul de coloane din tabela. "mask" este o masca folosita la codificare (codificarea se face pe linii).

In programul C avem un vector de "Acoperiri" ("ac") de dimensiune 512 (alocat static). Numarul 512 reprezinta numarul maxim de minimizari posibile, deoarece numarul maxim de mintermi este 1024, dar s-ar minimiza si deci daca alocam 1024 era prea mult. 512 este suficient (s-a luat ca la tabla de sah: jumatatea):

Functia "validare":

int validare (char *s, int min, int max, int aux).

Functia are ca argumente un vector de caracter (pentru a scrie un mesaj), doi intregi "min" si "max" care reprezinta capetele intervalului in care se poate introduce corect numarul respectiv si o valoare auxiliara notata cu "aux" care este folosita numai cand vrem sa validam citirea numarului de variabile (atunci ia valoarea -1).

Am facut aceasta functie pentru a avea posibilitatea de a introduce corect atat numar de variabile, numarul de mintermi, cat si mintermii functiei daca in prealabil s-a gresit. Functia returneaza un intreg si afiseaza un mesaj pe ecran.

Functia "minimizare":

void minimizare()

Functia "minimizare" este partea importanta a programului. Aici se fac toate minimizarile posibile!

Cum lucreaza functia?

Mintermii functiei sunt retinuti dupa codul binar in tabela. Atentie: tabela este in cod direct! Se parcurge tabela. Intai pe linii si apoi pe coloane. Conditia este ca pe linia si coloana respectiva, in tabela sa avem 1. Daca am gasit un minterm care nu este minimizat, atunci elementul respectiv devine 2 (pentru a tine seama la pasul urmator de faptul ca a fost parcurs). In acest caz marimea acoperirii curente devine 1, se aloca memorie pentru o celula de lista simplu inlantuita si mintermul este introdus in lista. Se recreeaza minterminul respectiv, in binar, dupa linie si coloana. "ultim" este ultimul element din acoperirea curenta (cand se adauga in lista trebuie sa stim adresa primului element si cea a ultimului element), iar "ultim->next" pointeaza la null. Pentru mintermul gasit se variaza pe rand toti bitii si se creaza termenul cu bitul schimbat care devine posibil vecin. Pentru acest nou minterm se calculeaza pozitia sa in tabela. Daca in tabela pe pozitia respectiva avem 1 inseamna ca am gasit un vecin. Se introduce si acest minterm in lista si se noteaza in matrice cu 2 (pentru a nu mai fi parcurs). Astfel obtinem o acoperire de 2 (dispare o variabila).

Pasul n:

Presupunem ca in minimizare avem 2ⁿ mintermi. Se ia primul minterm din lista si se variaza un bit, bitul de pe pozitia "i". Se parcurge lista pana la "ultim" (ultimul element din lista) . Se cauta in matrice daca exista mintermii din lista cu bitul "i" schimbat. Daca nu exista toti se iese fortat si se variaza alt bit. Daca exista toti, atunci se parcurge lista pana la ultimul element curent ("ultim_old"). Se aloca memorie pentru 2ⁿ celule de lista (2ⁿ reprezentand numarul de mintermi in acoperirea curenta - asa am presupus). Aceasta se realizeaza cu ajutorul unei noi variabile de tip "Acoperire". Pentru fiecare celula nou creata se introduc, in ordine, mintermii care au pe pozitia "i" bitul variat si se face legatura cu lista prin "ultim->next" care pointeaza catre noua celula. Astfel obtinem o acoperire de 2ⁿ⁺¹.

Dupa ce am variat toti bitii posibili, adica pana la numarul de variabile, se trece la urmatoare acoperire, deci "k" se incrementeaza.

La final vom avea toate acoperirile posibile in vectorul de liste, "ac", in care este retinuta si marimea acoperirii respective.

Cautarea "vecinilor" se face in cruce pe cod Grey pentru aceasta functie.

Functia "main":

void main (int argc, char **argv),

unde "argc" reprezinta numarul argumentelor din linia de comanda, iar "argv" este un vector de sir de caractere.

Functia are urmatoarele variabilele interne:

int max, i, j, temp1, temp2, bool, afisare,

FILE *in, *out.

Variabila "bool" este folosita ca o variabila booleana, ia doar valorile 1 si 0. 1 daca se intra in mod interactiv si 0 daca se intra in mod linie de comanda. Variabila "afisare" este folosita pentru afisarea functiei minimizate numai atunci cand s-au introdus toti mintermii posibili, adica atunci cand functia devine identic 1. Variabilele "in" si "out" sunt de tipul "FILE" (fisire), pentru modul de lucru linie de comanda. Se citeste din fisierul "in" si se scrie in fisierul "out".

Mod interactiv:

Se citesc de la tastatura: numarul de variabile, numarul de mintermi ai functiei si mintermii respectivi. Mintermii sunt cititi si sunt in acelasi timp introdusi in tabela.

Se aplica functia "minimizare". Dupa aplicarea functiei, avem toate minimizarile.

Afisarea:

Se parcurg toate acoperirile gasite, in numar de "k". Se iau 2 variabile locate: "term" si "not_term". Termenul nenegat va deveni "ac[k].lista->term". Termenul negat va fi "sau-exclusiv" intre termenul nenegat si numarul maxim care poate fi dat 1023 (in binar acesta este 1111111111). Se foloseste o variabila locala, de tip "Acoperire" pentru a parcurge lista curenta si termenii (nenegat si negat) vor deveni: "term & p->term", respectiv "not_term & (p->term ^ 1023)". Astfel se retin bitii 1 din primul element (in "term") neschimbati (1 in 1), si toti bitii care s-au schimbat din 0 in 1 (in "not_term" bitii respectivi vor fi 1).

Se parcurg toti bitii (pana la numarul de variabile). Daca bitul "i" este 1 in "term" atunci variabila este nenegata, iar daca este 1 in "not_term" inseamna ca este negata si afiseaza.

Mod linie de comanda:

Este analog cu modul interactiv numai ca se pun conditiile ca sa existe fisierele de intrare si iesire. Daca nu exista (fie doar unul, fie amandoua) va aparea pe ecran un mesaj de eroare. Daca exista atunci din fisierul de intrare citeste, in urmatoarea ordine: numarul de variabile, numarul de mintermi ai functiei si mintermii, iar in fisierul de iesire se va scrie minimizarea functiei.

2.1. Listarea codului sursa

# include <stdio.h>

# include <conio.h>

# include <alloc.h>

unsigned char tabela [32][32];

int nrvar, terms;

int k;

int vvar;

int ovar;

int mask;

typedef struct A Acoperire;

typedef struct A1 Acoperiri;

Acoperiri ac [512];

int validare (char *s, int min, int max, int aux) while ((scanf ('%d', &temp) != 1) || (temp < min) || (temp > max));

return temp;

void minimizare()

if (p == NULL)

}

}

}

k++;

void main (int argc, char **argv)

out = fopen (argv [2], 'w');

if (out == NULL)

fscanf (in, '%d', &nrvar);

}

max = 1 << nrvar;

vvar = (nrvar + 1) / 2;

ovar = nrvar - vvar;

mask = (1 << vvar) - 1;

if (bool == 1)

}

else

}

minimizare();

if (bool == 1)

else

for(j = 0; j < k; j++)

if (bool == 1)

else if (not_term & (1 << i))

if (j < k-1) printf (' + ');

if (afisare == 0) printf ('1');

printf ('n');

}

else

else if (not_term & (1<<i))

if (j < k-1) fprintf (out, ' + ');

if (afisare == 0) fprintf (out,'%d',1);

}

if (bool == 1) printf ('nnn');

else

getch();