REZOLVAREA PROBLEMELOR DE TRANSPORT

REZOLVAREA PROBLEMELOR DE TRANSPORT

Probleme de transport

Problemele de transport apar frecvent in situatiile in care trebuie planificat modul de distribuire al bunurilor de la producatori la consumatori. Obiectivul obisnuit al acestor probleme este minimizarea costurilor de transport. Modelele de transport sunt o variatie a problemelor de programare liniara si presupun urmatoarele:

Obiectivul este minimizarea costurior totale de transport.

Costurile de transport sunt functii liniare in raport cu numarul de unitati transportate.

Cererea si oferta sunt exprimate in unitati omogene.

Costurile de transport pe unitate nu variaza cu cantitatea transportata.

Pentru a ilustra modul in care se pot rezolva problemele de transport prezentam urmatorul exemplu:

O companie dispune de trei fabrici si patru centre de distributie. Fabricile sunt plasate in Cluj, Bacau si Craiova. Capacitatile de productie ale fabricilor sunt:

Centrele de distributie sunt plasate in Deva, Iasi, Bucuresti, Brasov. Cererea pentru produsele companiei in aceste centre este:

Managementul ar dori sa determine cantitatea care ar trebui transportata de la fiecare fabrica la fiecare centru de distributie astfel incat costurile de transport sa fie minime.

Figura II.2.1 prezinta graficul cu cele 12 rute posibile. Un astfel de graf este numit graf de retea. Cercurile reprezinta nodurile retelei. Liniile care unesc nodurile se numesc arcuri. Fiecare punct de plecare si sosire este reprezentat printr-un nod, iar fiecare ruta posibila este reprezentata printr-un arc. In dreptul fiecarui nod este trecuta valoarea ofertei (pentru capacitatile de productie) sau a cererii (pentru centrele de distributie). Sensul de deplasare este indicat prin sageti. Costurile unitare de transport pentru fiecare ruta sunt prezentate in tabelul II.2.1 si pe fiecare arc din figura II.2.1.

Tabelul II.2.1 - Costurile unitare de transport pe fiecare ruta

Figura II.2.1 - Graful de retea atasat problemei

Pentru a rezolva problema de transport putem folosi programarea liniara. Vom utiliza variabile de decizie cu doi indici, primul indice indica nodul origine, al doilea nodul destinatie. Astfel x_ij indica numarul de unitati transportate de la fabrica i la centrul de distributie j.

Costul unitatilor transportate din Cluj este = 3*x₁₁+2*x₁₂+7*x₁₃+6*x₁₄

Costul unitatilor transportate din Bacau este = 7*x₂₁+5*x₂₂+2*x₂₃+3*x₂₄

Costul unitatilor transportate din Craiova este = 2*x₃₁+5*x₃₂+4*x₃₃+5*x₃₄

Suma acestor costuri este costul total de transport, valoare care trebuie minimizata deci functia obiectiv este:

Min (3*x₁₁+2*x₁₂+7*x₁₃+6*x₁₄+7*x₂₁+5*x₂₂+2*x₂₃+3*x₂₄+2*x₃₁+5*x₃₂+4*x₃₃+5*x₃₄)

In problemele de transport apar restrictii deoarece fiecare fabrica are o capacitate de productie limitata si fiecare centru de distributie are o anumita cerere. Fabrica din Cluj are o capacitate de productie de 5000 unitati. Numarul total de unitati transportate din fabrica de la Cluj este x₁₁+x₁₂+x₁₃+x₁₄, deci restrictia asociata acestei fabrici este:

x₁₁+x₁₂+x₁₃+x₁₄ £ 5000

In mod similar pentru celelalte fabrici avem:

x₂₁+x₂₂+x₂₃+x₂₄ £ 6000 - pentru fabrica de la Bacau.

x₃₁+x₃₂+x₃₃+x₃₄ £ 2500 - pentru fabrica de la Craiova.

In cele patru centre de distributie, restrictia va fi data de faptul ca cererea la centrul respectiv trebuie sa fie egala cu cantitatile transportate aici.

x₁₁+x₂₁+x₃₁+x₄₁ =6000 - cererea la Deva

x₁₂+x₂₂+x₃₂+x₄₂ =4000 - cererea la Iasi

x₁₃+x₂₃+x₃₃+x₄₃ =2000 - cererea la Bucuresti

x₁₄+x₂₄+x₃₄+x₄₄ =1500 - cererea la Brasov

Combinand functia obiectiv cu restrictiile obtinem modelul pentru problema de transport:

Min (3*x₁₁+2*x₁₂+7*x₁₃+6*x₁₄+7*x₂₁+5*x₂₂+2*x₂₃+3*x₂₄+2*x₃₁+5*x₃₂+4*x₃₃+5*x₃₄)

x₁₁+x₁₂+x₁₃+x₁₄ £ 5000

x₂₁+x₂₂+x₂₃+x₂₄ £ 6000

x₃₁+x₃₂+x₃₃+x₃₄ £ 2500

x₁₁+x₂₁+x₃₁+x₄₁ =6000

x₁₂+x₂₂+x₃₂+x₄₂ =4000

x₁₃+x₂₃+x₃₃+x₄₃ =2000

x₁₄+x₂₄+x₃₄+x₄₄ =1500

x_ij³0, i=1,2,3; j=1,2,3,4

Rezolvarea problemei in Excel

Foaia de calcul folosita pentru rezolvarea problemei este prezentata in figura II.2.2.

Figura II.2.2 - Foaia de calcul atasata problemei

Datele problemei sunt introduse in domeniul A1:F8. Costurile de transport sunt continute in domaniul B5:E7, capacitatile de productie (oferta) in F5:F7, iar cererea din centrele de distributie in celulele B8:E8.

Elementele cheie care trebuie introduse in Excel sunt variabilele de decizie, functia obiectiv, partea stanga si partea dreapta a restrictiilor.

Se rezolva problema utilizand Solver-ul. Caseta de dialog Solver Parameters se completeaza ca in figura II.2.3. Optiunile selectate sunt Assume Linear Model si Assume Non-Negative.

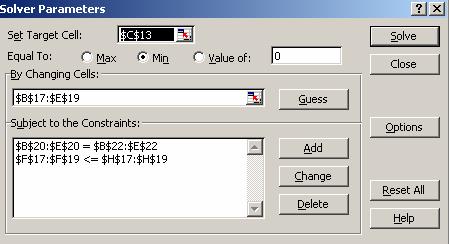
Figura II.2.3 - Caseta de dialog Solver

Solutia optima arata ca costul minim de transport este de 39500 u.m., iar in domeniul B17:E19 sunt afisate cantitatile care trebuie transportate pe fiecare ruta. Valoarea 0 indica ca pe ruta respectiva nu se transporta nimic.

Variatii ale problemelor de transport

Oferta totala nu este egala cu cererea totala

In multe cazuri oferta totala nu este egala cu cererea totala. Daca oferta totala depaseste cererea totala nu este necesara nici o modificare in problema de programare liniara. Excesul de oferta va aparea ca o abatere in solutia problemei, iar aceste abateri pot fi interpretate ca oferta neutilizata sau cantitati netransportate.

Daca oferta totala este mai mica decat cererea totala modelul de programare liniara a problemei de transport nu are o solutie fezabila. Pentru rezolvarea problemei se creeaza o oferta fictiva astfel incat excesul de cerere sa fie satisfacut si se atribuie costurilor de transport din acest punct valoarea 0. In acest mod problema de programare liniara va avea solutie.

Maximizarea functiei obiectiv

In unele probleme obiectivul este gasirea unei solutii care maximizeaza venitul sau profitul. Utilizand venitul sau profitul unitar in coeficientii functiei obiectiv, se va rezolva o problema de maximizare in locul uneia de minimizare. Modificarile nu afecteaza restrictiile.

Rute neacceptate

Stabilirea unei rute de la fiecare nod origine la fiecare nod destinatie nu este intotdeauna posibila. Pentru a rezolva aceste situatii se elimina din graful de retea arcele respective, iar din modelul de programare liniara variabilele de decizie corespunzatoare. Pentru a face cat mai putine modificari in foaia de calcul, pentru aceste rute se stabilesc costuri foarte mari, astfel incat pe aceste rute se vor efectua transporuri doar daca nu exista alte solutii fezabile.

Rute cu capacitati limitate

Pentru rutele cu capacitati limitate se introduc restrictii suplimentare. De exemplu, daca mijloacele de transport pe ruta Craiova - Deva nu pot transporta mai mult de 1000 de unitati se va introduce restrictia x₁₃£1000.

Modelul general de programare liniara al unei probleme de transport cu m puncte de origine si n puncte de destinatie este:

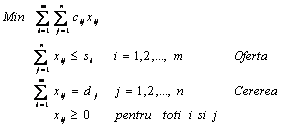
unde:

i = index-ul pentru punctele de origine

j = index-ul pentru punctele de destinatie

x_ij = numarul de unitati transportate de la originea i la destinatia j

c_ij = costul unitar de transport din originea i la destinatia j

s_i = oferta sau capacitatea din originea i

d_j = cererea la destinatia j