HARTI SI PLANURI.

Planul topografic este o reprezentare conventionala, micsorata si asemenea a unei portiuni relativ restrinse a terenului, care, prin detaliile pe care le contine, permite formarea unei imagini sugestive asupra planimetriei si reliefului terenului. La intocmirea lui nu se tine seama de influenta curburii Pamintului.

Harta topografica, spre deosebire de plan, reprezinta o suprafata mai mare de teren, imaginea pe care o reda este generalizata, adica nu contine toate detaliile dintr-un plan, iar la intocmirea ei se tine seama de curbura Pamintului. Pentru aceasta este necesar mai intai sa se creeze o retea geografica de paralele si meridiane in vederea reprezentarii suprafetelor curbe de pe sferoid.

Scara planurilor si hartilor.

Raportul constant intre o distanta de pe harta si omoloaga ei din teren poarta denumirea de scara. Dupa modul de prezentare, se disting:

a).scara numerica, cu forma generala :

[2.1]

in care, cunoscand doua valori, se poate determina a treia. Dupa marimea numitorului scarii, n, se disting:

scari mari, la care numitorul este mic, folosite la planurile topografice (1:1000, 1:500, etc);

scari mijlocii, folosite la hartile topografice (1:5000, 1:10000, ., 1:50000);

scari mici, la care numitorul este mare, folosite la hartile geografice (1:100000, .,1:1000000).

b).scara grafica, care este reprezentarea grafica a scarii numerice, permitand determinarea directa, in unitati din teren, a lungimii ce se doreste a se determina. Dupa constructie, pot fi scari grafice simple sau transversale.

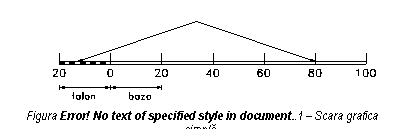
Scarile grafice simple (figura 2.1) fac posibila citirea distantei cu o precizie de pana la 1/10 din valoarea bazei. Orice scara grafica simpla este alcatuita dintr-un numar intreg de baze situate in dreapta originii scarii si un talon situat la stanga originii. Acesta este divizat in 10 intervale de lungimi egale, lungimea talonului fiind egala cu lungimea unei baze. Determinarea distantei intre doua puncte de pe harta se face luandu-se aceasta lungime in deschiderea unui compas sau distantier si asezand apoi compasul cu un varf pe o baza intreaga astfel ca al doilea varf sa se gaseasca in interiorul talonului.

Distanta se determina prin insumarea numarului de baze intregi cu partea fractionara, reprezentata de distanta determinata in interiorul talonului. Distanta corespunzatoare exemplului din figura 2.1 este de 95 m compusa fiind din 4 baze a cate 20 m fiecare si din partea zecimala reprezentata de 7,5 diviziuni a cate 2 m fiecare.

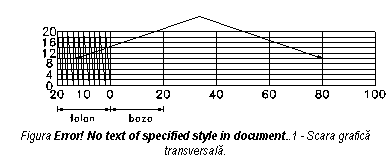
Scarile grafice compuse sau transversale (figura 2.2.), la care este posibila citirea pina la 1/100 din valoarea bazei. Acest tip de scara este perfectionat fata de scara grafica simpla, in sensul ca acum este posibila obtinerea unei precizii de 1/100 din valoarea bazei. Modul de utilizare este asemanator cu cel prezentat anterior : distanta de pe harta se ia in deschiderea compasului si se aplica apoi pe scara grafica astfel ca un capat al compasului sa se afle pe o baza intreaga iar cel de al doilea capat in interiorul talonului, exact pe un punct de intersectie al orizontalelor cu transversalele. Trebuie avut grija ca ambele capete ale compasului sa se afle pe aceeasi orizontala.

Scarile grafice servesc fie la determinarea unei distante de pe harta, fie la raportarea pe harta a unei distante masurata in teren. Contractia hartiei planului si modalitati de eliminare a acesteia, constitue un fenomen inerent, datorat conditiilor de pastrare si manipulare a hartilor, ca urmare a conditiilor de temperatura si umiditate ale mediului ambiant, care se modifica permanent. Fenomenul poate afecta hartile pana la un cuantum de 2% pe orice directie. Pentru eliminarea acestui inconvenient, fie odata cu tiparirea hartii se tipareste si scara grafica, fie inainte de tiparire hartia se lipeste (se casereaza) pe un suport nedeformabil (zinc, sticla, material plastic, etc.)

Precizia grafica a scarii este un rezultat al faptului ca este imposibil de determinat distanta "d" cu o precizie mai mare de 0,1mm, dar care in mod obisnuit are valori de 0,2-0,3mm. Acestor erori le corespunde in teren o lungime ce depinde de scara hartii. Pentru determinarea acestei marimi se porneste de la definitia scarii numerice si anume:

[2.2]

Din relatia [2.2] se poate observa ca, cu cat numitorul scarii este mai mare, deci scara este mai mica, cu atat precizia de citire si raportare a distantelor este mai mica.

Functie de scara la care sunt redactate, produsele cartografice se clasifica in:

planuri topografice cu scara cuprins in general intre 1:1000 si 1:10000;

harti topografice cu scara mare, pana la 1:100000;

harti topografice de ansamblu cu scari medii, pana la 1:200000 sau 1:1000000;

harti geografice la scari mai mici de 1:1000000

Semnele conventionale

Detaliile din teren se reprezinta pe planuri si harti prin semne astfel concepute incat sa fie cat mai sugestive, mai usor de reprezentat prin desen. Acestea pot reprezenta pe planuri sau harti detalii planimetrie si altimetrice, intr-o forma cit mai sugestiva, putandu-se clasifica dupa destinatia detaliilor pe care le reprezinta in semne de planimetrie si semne de altimetrie.

Semne pentru planimetrie, care se impart in :

semne de contur, care permit desenarea la scara hartii a naturii detaliilor (mlastini, paduri, etc). In cazul padurilor se reprezinta numai conturul padurii nu si pozitia arborilor in padure.

semne de pozitie sau de scara, care folosesc pentru redarea detaliilor care nu se pot reprezenta la scara. Ele arata insa pozitia exacta a detaliului pe care-l reprezinta.

semne explicative, care 'explica' anumite detalii de pe harta. Aceasta categorie se foloseste numai impreuna cu celelalte semne conventionale. La reprezentarea unei paduri, in afara conturului paduri, din loc in loc se foloseste un semn conventional care precizeaza specia preponderenta a arborilor.

Semne pentru altimetrie se folosesc la reprezentarea formelor de relief, cum ar fi dealurile, varfurile, vaile, rapele, etc.

Semnele conventionale folosite la redactarea hartilor sau planurilor sunt cuprinse in atlase de semne conventionale. Cateva exemple sunt prezentate in figura 2.3.

Reprezentarea reliefului.

Relieful cuprinde totalitatea neregularitatilor, convexe si concave ale terenului, iar reprezentarea lui cit mai corecta si expresiva este foarte importanta. Pentru aceasta se folosesc urmatoarele metode : curbe de nivel, planul cotat, planuri in relief, umbre cu tente.

Dintre toate metodele, cea mai folosita este cea a curbelor de nivel. O curba de nivel este locul geometric al punctelor care au aceeasi cota, proiectat in plan orizontal. Se obtin prin sectionarea terenului cu suprafete plane orizontale, iar proiectia in plan orizontal al urmei sectiunii este chiar curba de nivel.

Pentru reprezentarea curbelor de nivel, in functie de scara hartii, se alege o echidistanta, E, reprezentand distanta pe verticala intre doua suprafete de sectiune a terenului (figura 2.4).

Aceasta marime se numeste echidistanta numerica sau naturala; ea depinde de accidentatia terenului, de scara hartii si de precizia cu care se doreste a fi reprezentat relieful. Se considera ca intre doua curbe de nivel panta terenului este constanta, iar acest lucru se obtine prin selectarea punctelor care se masoara astfel ca la schimbarea pantei sa se determine, prin masurare, obligatoriu, un punct. Curbele de nivel se clasifica in functie de valoarea echidistantei E. Valoarea acesteia este functie de scara planului sau hartii si este in general de 5 m pentru scara 1:25000, 10 m pentru scara 1:50000 si 20 m pentru scara 1:100000. Indiferent de scara, culoarea pentru prezentarea curbelor de nivel pe planuri sau harti este culoarea sepia (maro-roscat).

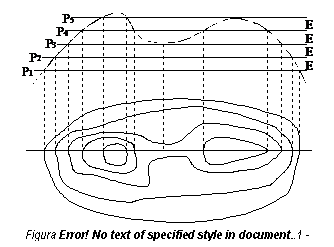
Forma unei curbe de nivel este cea de linie curba cu contur inchis, indiferent de configuratia terenului reprezentat. Functie de echidistanta dintre ele, curbele de nivel se impart in :

normale, reprezentate prin linii subtiri, cu grosime uzuala de 0,15 mm, dispuse in contururi inchise, distanta pe verticala intre doua curbe de nivel normale fiind egala cu echidistanta.

principale, reprezentate prin linii mai groase, cu grosime uzuala de 0,25 mm, distanta pe verticala intre doua curbe principale fiind egala cu 5E;

ajutatoare, trasate prin linii subtiri, intrerupte, avand distanta pe verticala egala cu E. Se traseaza numai atunci cand se considera ca densitatea curbelor normale este insuficienta si nu are loc o redare exacta a configuratiei terenului. Acest tip de curbe de nivel se poate reprezenta prin linii curbe deschise, numai pe zonele unde curbele de nivel normale sunt rare.

auxiliare, trasate prin linii intrerupte, mai scurte decat cele ajutatoare, avand echidistanta de E. Si acestea sunt curbe deschise, reprezentate sporadic numai acolo unde este necesar.

Normala aproximativa la doua curbe de nivel se numeste linie de cea mai mare panta. Pentru a se indica sensul de scurgere al apei, curbele de nivel sunt insotite de mici linii numite "bergstrich"-uri. Pozitionarea in interiorul curbei a begstrich-ului indica o forma de relief care "tine apa", dupa cum pozitionarea pe exteriorul curbei indica curgerea apei.

Forme tip de relief.

Totalitatea si complexitatea formelor de relief se poate reduce la trei tipuri caracteristice:

sesuri, care reprezinta suprafetele de teren plane, cu diferente de nivel nesemnificative, ce reprezinta o campie daca terenul se afla la mai putin de 200 m deasupra nivelului marii, sau podis daca se afla la peste 200 m deasupra nivelului marii;

inaltimile, care reprezinta forme tip de relief, cu diferente de nivel pozitive, sensibil diferite de zona inconjuratoare

depresiunile, care reprezinta forme tip de relief, cu diferente de nivel negative, sensibil diferite de zona inconjuratoare

Forme tip de inaltimi.

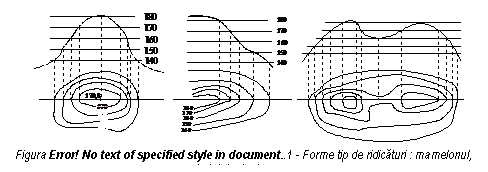
Mamelonul este o ridicatura cu inaltime de 50 - 150 metri mai mari fata de terenul inconjurator, cu virf rotunjit si pante relativ simetrice care sunt dispuse in toate directiile. Se reprezinta prin curbe de nivel inchise (figura 2.5).

Piscul se reprezinta asemanator cu mamelonul numai ca pantele fiind mai abrupte, curbele de nivel vor fi mai dese decat la reprezentarea mamelonului.

Dealul este o ridicatura cu doi versanti, despartiti prin culme sau creasta. Se reprezinta ca un diedru convex. Elementele caracteristice sunt linia de despartire a apelor, virful si piciorul crestei. Se poate intalni si sub denumirea de crupa, creasta sau bot de deal.

Saua este forma de relief care racordeaza doua creste sau mameloane. Centrul seii se numeste git si formeaza originea a doua vai care sunt dispuse transversal pe linia de creasta.

Forme tip de adancimi.

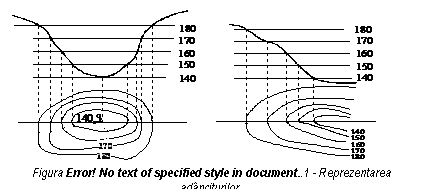
Caldarea este forma inversa a mamelonului. Se caracterizeaza prin margine, perete si fund. Reprezentarea se face prin curbe de nivel inchise, ale caror valori cresc din interior spre exterior.

Valea este depresiunea formata de doi versanti care coboara si se unesc pe fundul vaii. Este reprezentata de un diedru concav. Caracteristicile vaii sunt determinate de firul vaii sau talvegul, originea si gura vaii. Ca arie, valea se desfasoara pe suprafete intinse. Ca mod de reprezentare prin curbe de nivel, acestea sunt alungite, cu concavitatea spre firul vaii (talveg). Viroaga sau crovul reprezinta o vale de intindere mai mica, caracteristica regiunilor de ses, formarea ei datorandu-se actiunii erozive a torentilor in roci moi. Este omoloaga vaii pentru zonele de campie. Aceste forme de relief se reprezinta prin curbe de nivel asa cum este aratat in figura 2.6.

Bazinul hidrografic.

Este o forma complexa, inchisa pe trei parti de linia de despartire a apelor si deschisa pe o latura. In interiorul unui bazin hidrografic, apele sunt colectate de pe versanti si evacuate prin latura deschisa, iar din punct de vedere al alcatuirii, acesta se compune din mai multe forme de relief simple : mameloane, sei, vai. Astfel, intre doua forme de relief de tip mamelon exista totdeauna o sa ce va constitui obarsia unei vai. La randul lor, aceste vai mai mici se vor uni in puncte de confluenta si vor forma o vale majora ce va colecta apele intregului bazin hidrografic. Din cele prezentate in figura 2.7, se poate vedea ca bazinul hidrografic este definit ca suprafata de pe care in mod natural apa pluviala este colectata si evacuata la vale.

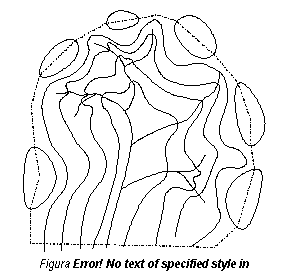
Importanta cunoasterii intinderii bazinului hidrografic pentru un curs de apa este utila in cazul proiectarii constructiilor hidrotehnice pentru stabilirea volumului potential de apa dintr-un viitor lac de acumulare pentru o hidrocentrala.

In cazul proiectarii podurilor aferente unei cai de comunicatii, cunoasterea bazinului hidrografic permite calculul volumului de apa ce va trece pe sub viitorul pod, fapt ce permite calculul inaltimii libere a podului.

Folosirea planurilor si hartilor.

Determinarea coordonatelor rectangulare.

Pentru determinarea coordonatelor plane ale unui punct pe o harta sau plan se utilizeaza caroiajul kilometric, care este o retea de patrate, trasata numai pe harta si inexistenta in teren, avand latura de 1km in teren, trasate pentru valori kilometrice intregi. Determinarea poate sa tina sau poate sa nu tina cont de deformatia hartiei planului.

In cazul in care trebuie sa se tina cont de deformatia hartiei planului, se determina coeficientii pe cele doua directii - x si y - ale planului, coeficienti care au expresiile:

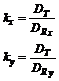[2.3]

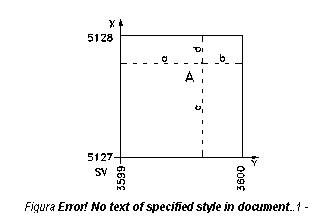
in care D_T = distanta teoretica intre doua linii de caroiaj succesive, D_Rx , respectiv D_Ry , distantele reale intre aceleasi doua linii de caroiaj, pe directia x respectiv y. Distantele de mai sus se calculeaza functie de scara planului in cazul lui D_T, respectiv se masoara cu mare atentie cu o rigla si se transforma in unitati din teren, in cazul lui D_Rx, respectiv D_Ry.

Relatiile de calcul pentru coordonatele plane X si Y sunt :

[2.4]

in care X_SV si Y_SV sunt coordonatele coltului de sud-vest al caroiajului in care se gaseste punctul ale carui coordonate se determina; n este numitorul scarii; a, c reprezinta segmentele masurate pe harta, pe paralelele duse prin punct la axele de coordonate (figura 2.8)

Daca determinarea coordonatelor nu tine cont de deformatia hartiei planului, in relatiile 2.4 valoarea coeficientilor k_x respectiv k_y va fi egala cu 1.

Dar problema se poate pune si invers, in sensul ca date fiind coordonatele unui punct din teren se cere ca acesta sa fie raportat pe harta. Pentru rezolvarea problemei se vor calcula segmentele corespunzatoare fractiunilor de kilometri pentru cele doua coordonate, se va alege coltul de sud-vest si se vor raporta segmentele calculate pe axele de coordonate. La intersectie se va gasi punctul determinat in teren.

Determinarea distantei intre doua puncte pe harta.

Pentru solutionarea problemei, se vor analiza mai intai datele referitoare la configuratia distantei sub aspect geometric si apoi elementele cunoscute. Se pot distinge urmatoarele cazuri:

a).cind distanta intre cele doua puncte este un aliniament, acesta se poate determina fie:

folosind coordonatele punctelor care determina distanta, cu relatia :

[2.5]

folosind scara numerica a hartii : se masoara cu o rigla distanta dintre capetele distantei, iar valoarea se multiplica cu numitorul scarii si se transforma in unitati din teren. Masurarea se va face cu mare atentie, pina la zecime de milimetru.

folosind scara grafica a hartii : se ia in deschiderea compasului distanta ce se doreste a se determina si prin pozitionarea convenabila a compasului pe scara grafica, se obtine direct distanta corespunzatoare in unitati din teren.

b).cind distanta intre puncte are un traseu sinuos, pentru determinarea distantei se foloseste un instrument, numit curbimetru, care permite urmarirea traseului cu ajutorul unei rotite cuplate la un contoar ce afiseaza direct distanta functie de scara hartii.

Determinarea orientarii unei directii.

Acest tip de problema se poate rezolva fie folosind raportorul si procedand la o masurare directa intre directia nordului (reprezentata de o paralela la liniile verticale de caroiaj, linie ce trece prin punct) si directia de masurat, fie folosind functiile trigonometrice, tangenta sau cotangenta, calculate folosind coordonatele cunoscute sau determinate ale punctelor intre care se doreste a se afla orientarea. Astfel:

[2.6]

sau

[2.7]

Se va utiliza acel raport care este subunitar. Relatiile sunt valabile in situatia in care axa Ox este pe verticala si Oy pe orizontala.

Orientarea in teren a hartilor sau planurilor.

Este operatiunea prin care linii de pe harta sau plan devin paralele cu omoloagele lor din teren si au aceeasi directie. In aceasta situatie, toate detaliile ce se afla de o parte a unei directii in teren se afla de aceeasi parte a directiei si pe harta. Acesta operatiune se poate face si cu busola, situatie in care directia nordului magnetic al hartii este suprapusa peste directia nordului magnetic determinata in teren cu ajutorul busolei.

Determinarea cotelor prin interpolarea curbelor de nivel.

Daca punctul este chiar pe curba de nivel, cota lui va fi egala cu valoarea curbei de nivel. In caz contrar, se duce prin punct linia de cea mai mare panta (numita si normala aproximativa la cele doua curbe), reprezentata de cea mai scurta distanta intre cele doua curbe, trecind prin punct (figura 2.9). Se masoara cu o rigla distanta D intre curbe, precum si distanta d de la una din curbe la punct. Utilizind relatia:

[2.8]

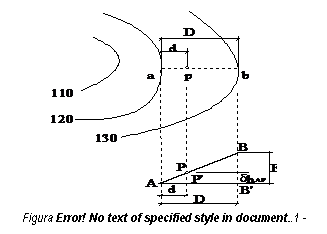
unde E este echidistanta curbelor de nivel este posibila datorita triunghiurilor asemenea APP' si ABB'.

Cota punctului P rezulta insumand algebric valoarea calculata cu valoarea curbei de nivel corespunzatoare segmentului d. Valoarea obtinuta pentru d h_AP trebuie sa fie mai mica decat echidistanta.

Determinarea pantei liniei terenului intre doua puncte.

Panta terenului reprezinta inclinarea suprafetei terenului fata de orizontala si este chiar tangenta unghiului de inclinare (figura 2.10).

Relatia generala de calcul este:

[2.9]

in care d h reprezinta diferenta de nivel cu semn algebric intre punctele de capat, iar D reprezinta distanta orizontala din teren intre cele doua puncte.

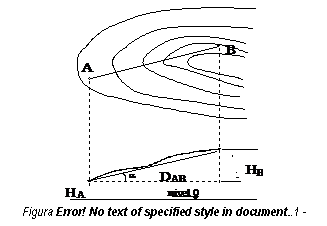
Ca mod de exprimare, aceasta se poate exprima fie asa cum rezulta din relatia 2.9, fie sub forma procentuala, adica:

[2.10]

sau in grade, minute si secunde

Trasarea liniei de panta constanta intre doua puncte pe harta.

Aceasta problema apare cind se doreste trasarea axului unei cai de comunicatie, axul unui canal, sau orice situatie in care se impune alegerea unui traseu a carui panta trebuie sa fie egala sau mai mica decat o valoare impusa. Problema se reduce la calculul unor distante d_i pe plan, astfel ca omoloagele lor D_i din teren sa aiba panta p% egala sau mai mica decat valoarea impusa.

Pornind de la formula pantei exprimata sub forma procentuala:

[2.11]

se obtine :

[2.12]

careia ii corespunde distanta d_i de pe harta,

[2.13]

Se disting trei situatii, functie de valorile pe care le poate lua dh, si anume:

cand valoarea lui dh este egala cu echidistanta curbelor de nivel, distanta pe harta este data de relatia:

[2.14]

cand punctul A nu se afla pe curba de nivel, valoarea distantei d se calculeaza cu relatia:

[2.15]

cand punctul B nu se afla pe curba de nivel, valoarea distantei d se calculeaza cu relatia:

[2.16]

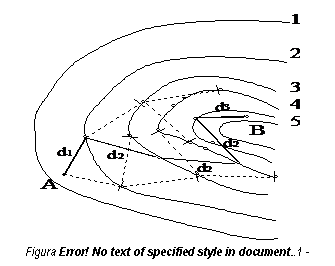
Distantele d se numesc pas de proiectare. Trasarea pe plan sau harta a liniei de panta data se face astfel : in deschiderea compasului se ia distanta d₁ si cu varful compasului in punctul A se descrie un arc de cerc care intersecteaza prima curba de nivel in doua puncte. Se ia in deschiderea compasului distanta d₂, se aseaza varful, succesiv in punctele determinate anterior si se descriu arce de cerc, obtinand, pe a doua curba de nivel, in total patru puncte. Din aceste puncte se vor trasa cu acelasi pas de proiectare punctele de intersectie cu urmatoarea curba de nivel, si asa mai departe. Se observa ca numarul variantelor se dubleaza de fiecare data. Pentru a nu se incarca desenul inutil, se vor alege la trasare numai acele puncte care raspund la celelalte conditii de proiectare. De exemplu, pentru trasarea axului unui drum se vor alege acele variante care asigura unghiuri obtuze intre aliniamentele succesive.

Intocmirea profilului longitudinal

Prin sectionarea terenului cu un plan vertical trecand prin doua punctele se obtine profilul terenului intre acele puncte.

Pentru o reprezentare sugestiva, se alege scara inaltimilor de 10 ori mai mare decat scara lungimilor, de exemplu daca scara lungimilor este 1:25000, scara inaltimilor se va alege 1 : 2500. Cele doua scari reprezinta axe de coordonate, in care scara lungimilor se reprezinta pe orizontala si scara inaltimilor pe verticala (figura 2.12)

Se unesc printr-o dreapta punctele A si B si se noteaza punctele de intersectie ale dreptei cu curbele de nivel. Se iau in deschiderea compasului, succesiv, distantele de la punctul A la fiecare curba de nivel si se marcheaza punctele pe profilul longitudinal. Se determina corespondentul in teren al acestor distante si se precizeaza in rubrica corespunzatoare din cartusul profilului longitudinal.

Se calculeaza cotele punctelor A si B prin interpolarea curbelor de nivel, trecand valorile pe linia corespunzatoare cotelor din cartus. Se completeaza cotele punctelor de intersectie ale dreptei A-B cu curbele de nivel. Originea axei cotelor se alege astfel ca cea mai mica cota sa se reprezinte la circa 1-1,5 centimetri deasupra axei distantelor.

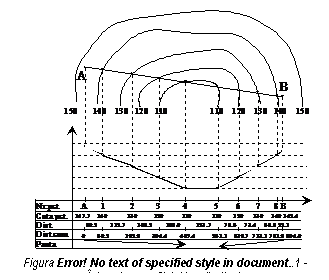
Pozitia punctului A pe profilul longitudinal se obtine la intersectia perpendicularei ridicate pe axa lungimilor cu perpendiculara pe axa cotelor care marcheaza valoarea cotei punctului A. Pozitia celorlalte puncte se obtine similar, la intersectia perpendicularelor pe cele doua axe. Punctele astfel obtinute pe profilul longitudinal se unesc prin linii drepte.

Determinarea suprafetelor pe harti si planuri.

O astfel de problema se rezolva functie de elemente geometrice ce se obtin prin masuratori pe harta sau plan. In principiu, se pot folosi metode numerice, grafice sau mecanice, iar unele din metodele ce se vor descrie se pot folosi si pentru determinarea suprafetelor din teren.

Metodele numerice.

Aceste metode utilizeaza relatii analitice, geometrice sau trigonometrice.

relatiile analitice se aplica in situatia in care sunt cunoscute coordonatele rectangulare ale tuturor punctelor ce definesc conturul a carui suprafata se cere determinata. Conturul se descompune in triunghiuri pornind de la unul din varfurile conturului. Suprafata unui triunghi se determina prin calcularea unui determinant continand pe primele doua coloane coordonatele x si y ale varfurilor triunghiului iar pe coloana a treia termenul 1. Pentru un triunghi cu varfurile notate cu i, j, k, se obtine relatia :

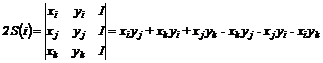[2.17]

Intreaga suprafata va rezulta ca suma suprafetelor triunghiurilor componente; prin insumarea si gruparea termenilor din relatiile de tipul de mai sus se obtine o relatie de tip generalizat de forma:

[2.18]

Prima suma apare cand gruparea termenilor se face dupa abscisele x_i, iar a doua cand gruparea se face dupa ordonatele y_i.

relatiile geometrice se aplica in situatia in care conturul suprafetei de determinat se poate imparti in triunghiuri la care se cunosc numai elementele liniare, fie ca este vorba de baze si inaltimi, fie ca este vorba numai de laturi. In cazul in care se cunosc numai laturi, relatia de calcul a suprafetei unui triunghi este:

[2.19]

unde p este semiperimetrul, iar a, b si c sunt laturile unui triunghi. Suprafata totala va fi suma celor 'n' triunghiuri componente.

Daca se cunosc baze si inaltimi in triunghiurile in care s-a descompus conturul, relatia de calcul a suprafetei unui triunghi va fi:

[2.20]

unde B si I sunt baza respectiv inaltimea unui triunghi, iar suprafata conturului este data de suma suprafetelor celor 'n' triunghiuri componente.

relatiile trigonometrice se folosesc in situatia in care in urma descompunerii conturului in triunghiuri, pentru acestea se cunosc atat elemente liniare cat si elemente unghiulare. Suprafata unui triunghi se va calcula in acest caz cu relatii de tipul:

[2.21]

iar suprafata conturului va rezulta ca suma suprafetelor triunghiurilor componente.

Metode grafice.

In situatia in care nu dispunem de coordonatele punctelor, elementele necesare determinarii suprafetelor urmand a se determina grafic, prin citire de pe plan. In acest context este evident ca suprafata va fi cu atat mai precis determinata cu cat lungimile de pe plan sau harta vor fi mai precis masurate grafic, deci scara hartii va fi mai mare.

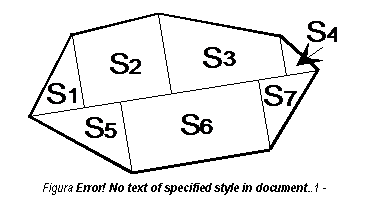
descompunerea in figuri geometrice simple, triunghiuri sau trapeze (figura 2.13) necesita masurarea pe plan a bazelor si inaltimilor in cazul triunghiurilor, respectiv a bazelor mici, bazelor mari si inaltimilor in cazul trapezelor. Functie de scara hartii, aceste lungimi se transforma in lungimi din teren ce vor fi utilizate la calcule.

Indiferent de figurile geometrice alese, se recomanda ca verificarea determinarilor sa se faca alegandu-se o alta varianta de descompunere, cu repetarea operatiunilor privind determinarea lungimilor si apoi a suprafetelor, urmand ca rezultatele celor doua determinari sa se compare intre ele.

metoda paralelelor echidistante sau metoda trapezelor se aplica pentru suprafete alungite (figura 2.14).Pe o foaie de hartie transparenta se traseaza o retea de linii paralele si echidistante. Se recomanda ca pentru o mai usoara folosire, sa se traseze si paralelele situate la jumatatea distantelor determinate de primele paralele. Aceasta retea se suprapune peste conturul de pe plan (figura 2.14).

In urma acestei operatiuni, conturul de pe plan a fost descompus intr-o succesiune de trapeze care vor avea toate inaltimile egale intre ele, iar baza mare a unui trapez devine baza mica in trapezul alaturat. Suprafata totala se obtine insumand suprafetele trapezelor, adica :

[2.22]

sau :

[2.23]

Daca este cazul, la aceasta valoare se adauga suprafata ramasa dintr-un trapez incomplet. Pentru controlul determinarii se procedeaza la o alta pozitionare a retelei de paralele si determinarea suprafetei functie de aceeasi inaltime a trapezelor, dar cu alte valori pentru b_i.

metoda patratelor module este folosita la determinarea suprafetelor cu contur neregulat. Pe o foaie de hartie transparenta se construieste o retea de patrate cu latura "a" (figura 2.15).

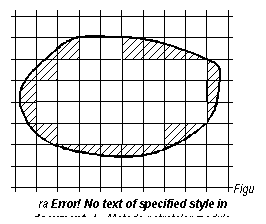
Se suprapune reteaua de patrate peste suprafata cu contur neregulat si se numara patratele intregi, n₁, apoi, prin aproximare, se determina n₂ , numarul patratelor incomplete. Suprafata totala va fi deci :

S = a² (n₁ + n₂) [2.24]

in care a² este suprafata unui patrat.

Pentru verificare, reteaua se amplaseaza intr-o alta pozitie si se face o noua determinare a suprafetei.

Metoda mecanica.

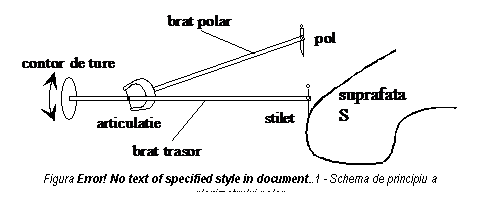
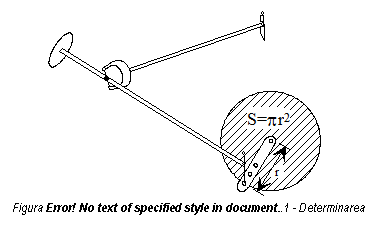
Ca si metodele grafice, metoda mecanica se foloseste in situatia in care nu dispunem de coordonatele punctelor de pe contur. Se va folosi in acest caz un instrument denumit planimetru. Functie de constructie, acesta poate fi polar, cu disc, liniar sau digital. Principiul metodei este aratat in figura 2.16.

Se poate vedea astfel ca polul planimetrului este, in cazul descris, in afara suprafetei de masurat; se poate insa ca acest pol sa fie situat si in interiorul suprafetei S.

Planimetrul polar se compune din bratul polar P si bratul trasor T sau bratul caruciorului, articulate intre ele in punctul O. Bratul trasor T, de lungime reglabila, urmareste, cu un capat prevazut cu un varf, conturul suprafetei S, iar la celalalt capat se inregistreaza miscarea stiletului pe conturul suprafetei prin intermediul unui contoar sau dispozitiv inregistrator.

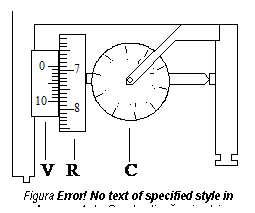
Polul bratului polar, cu lungime constanta, se fixeaza cu ajutorul unei contragreutati cu ac pe masa de lucru. Dispozitivul de inregistrare a miscarii planimetrului se compune dintr-un contoar si a ruleta integratoare. Citirile pe aceasta ruleta se fac cu ajutorul unui vernier (figura 2.17).

Pentru determinarea marimii suprafetei se porneste de la faptul ca suprafata unei figuri oarecare, planimetrate, este egala cu suprafata unui dreptunghi de lungime egala cu lungimea L a bratului trasor si latime egala cu o diviziune, r, a ruletei.

S = n *(r *L) [2.25]

Din aceasta relatie se constata ca unitatea de masura folosita la planimetrul polar este egala cu 10^-3 din (r * L), valoare ce provine din cele 10 diviziuni ale contoarului, 10 diviziuni ale ruletei si 10 diviziuni ale vernierului. Ea poarta denumirea de constanta de scara, K_s, fiind functie de scara planului si constanta pentru o lungime L a bratului trasor.

Valoarea numarului generator, n, din relatia [2.25] se determina prin diferenta intre citirea finala C_f si citirea initiala C_i, citiri efectuate la sfarsitul, respectiv inceputul parcurgerii conturului suprafetei S cu ajutorul stiletului. Daca se inlocuieste

n = C_f - C_i

in relatia [2.25], se obtine:

S = K_s (C_f - C_i) [2.26]

In vederea determinarii constantei de scara K_s, in trusa planimetrului polar exista o rigleta ce permite, ca prin fixarea stiletului pe unul din orificiile existente pe ea, sa se parcurga un cerc de raza data. In acest caz, suprafata cercului este cunoscuta, iar prin efectuarea diferentei intre citirile de la sfarsitul si de la inceputul parcurgerii circumferintei cercului sa se determine numarul generator, n.

Utilizand relatiile [2.25] si [2.26], se poate scrie ca:

[2.27]

Pentru o cat mai corecta valoare a diferentei citirilor, se procedeaza la parcurgerea de mai multe ori a conturului si calculul unei valori medii a diferentei citirilor.

In situatia cand valoarea obtinuta pentru constanta de scara nu este o valoare intrega (2, 5, 10, 20), se calculeaza o noua lungime a bratului trasor L' cu relatia:

[2.28]

unde K'_s este noua constanta de scara avand o valoare intrega. Dupa fixarea noii lungimi a bratului, L', se procedeaza la o verificare si eventual reajustare a planimetrului.

In cazul in care suprafata de planimetrat este mare, este posibil ca polul planimetrului sa fie amplasat in interiorul suprafetei. Relatia de calcul in acest caz va fi :

[2.29]

in care C reprezinta constanta planimetrului si este egala cu suprafata cercului de baza functie de lungimea bratelor, valoarea constantei fiind data in fisa tehnica a planimetrului. Semnele + sau - se folosesc functie de pozitia reciproca a suprafetei de planimetrat si a cercului de baza. Daca cercul de baza este in interiorul suprafetei, se foloseste semnul +, iar daca cercul de baza este in exteriorul suprafetei, se foloseste semnul -.

Pentru ca planimetrarea sa fie corecta, se impune respectarea urmatoarelor reguli:

planul sau harta se fixeaza pe o planseta orizontala si neteda;

bratele planimetrului sa formeze unghiuri cuprinse intre 30 si 150 pe tot conturul planimetrat;

ruleta se va deplasa pe o suprafata suficient de rugoasa pentru a asigura o aderenta optima;

deplasarea stiletului in sens orar pe conturul suprafetei conduce la obtinerea de valori pozitive ale suprafetelor determinate, in timp ce deplasarea in sens antiorar conduce la valori negative.

Marimea suprafetei determinata mecanic este afectata de o serie de erori care depind de scara planului, metoda de planimetrare si marimea suprafetei planimetrate. Toate aceste erori vor trebui sa fie mai mici, cel mult egale cu toleranta admisa T_s. Pentru determinari ale aceleasi suprafete, se impune o toleranta de :

[2.30]

iar daca se tine cont de scara planului, toleranta este data de relatia :

[2.31]