| CATEGORII DOCUMENTE |
| Arhitectura | Auto | Casa gradina | Constructii | Instalatii | Pomicultura | Silvicultura |
DOCUMENTE SIMILARE |
||
|
||
Se considera o placa dreptunghiulara cu
dimensiunile urmatoare( 0.5 [m] x 0.4
[m] ) si grosimea de 0.01 [m]. Conductivitatea termica a materialului placii
este ![]() . Frontiera vest a placii
primeste o densitate de flux de valoare constanta
. Frontiera vest a placii
primeste o densitate de flux de valoare constanta ![]() , iar frontierele sud si
est sunt izolate,frontiera nord fiind mentinuta la temperatura constanta de 100 [ºC].
, iar frontierele sud si
est sunt izolate,frontiera nord fiind mentinuta la temperatura constanta de 100 [ºC].
Sa se determine distributia stationara de temperatura si calculul temperaturilor in nodurile retelei de discretizare(1.30).
∆x = ∆y = 0.1 [m]
Solutie
Ecuatia diferentiala ce guverneaza transferul termic este:
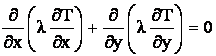
Se utilizeaza o retea de discretizare cu 30 de noduri uniform distribuite ca in figura :

Pentru un nod interior ecuatia discretizata este :
![]()
![]()
![]()
Ecuatiile discretizate pentru nodurile interioare ( 8, 9, 10, 11, 14, 15, 16, 17, 20, 21, 22, 23 ) ale domeniului de calcul sunt :

Pentru nodurile situate pe frontiera vest ( 2, 3, 4, 5 ) ecuatiile discretizate se obtin integrand ecuatia conductiei termice pe jumatatea de volum de control hasurat din figura :

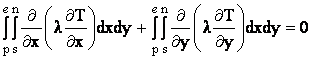
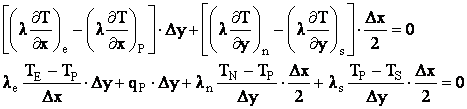
![]()
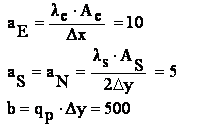
![]()

Pentru nodurile situate pe frontiera nord ( 26, 27, 28, 29 ) ecuatiile discretizate se obtin integrand ecuatia conductiei termice pe jumatatea de volum de control hasurat din figura :


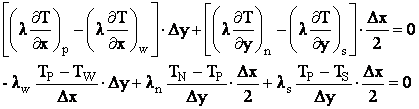
![]()
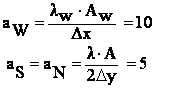
![]()

Pentru nodurile situate pe frontiera sud ( 7, 13 ,19 ) ecuatiile discretizate se obtin integrand ecuatia conductiei termice pe jumatatea de volum de control hasurat din figura :

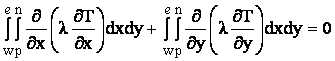
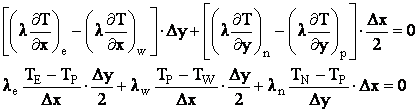
![]()
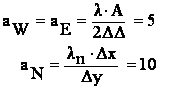
![]()
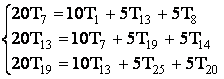
Pentru nodul 1 ecuatia discretizata se obtine integrand ecuatia conductiei termice pe sfertul de volum de control hasurat din figura :

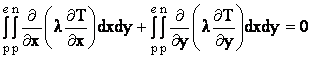
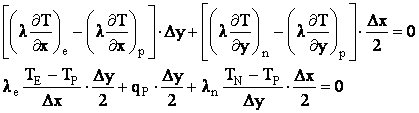
![]()
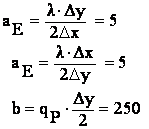
![]()
![]()
Pentru nodul 25 ecuatia discretizata se obtine integrand ecuatia conductiei termice pe sfertul de volum de control hasurat din figura :

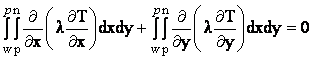
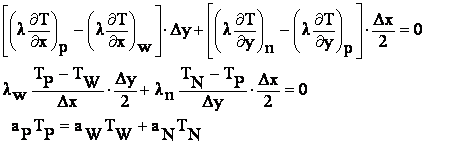
![]()
![]()
![]()
|
MVF 30 noduri |
MEF 31 noduri |
Eroarea |
MVF 546 noduri |
MEF 485 noduri |
Eroarea |
|
|
T1 | ||||||
|
T2 | ||||||
|
T3 | ||||||
|
T4 | ||||||
|
T5 | ||||||
|
T7 |
| |||||
|
T8 | ||||||
|
T9 | ||||||
|
T10 | ||||||
|
T11 | ||||||
|
T13 | ||||||
|
T14 | ||||||
|
T15 | ||||||
|
T16 | ||||||
|
T17 | ||||||
|
T19 | ||||||
|
T20 | ||||||
|
T21 |
| |||||
|
T22 | ||||||
|
T23 | ||||||
|
T25 | ||||||
|
T26 | ||||||
|
T27 | ||||||
|
T28 | ||||||
|
T29 |
Graficul in MATCHAD 7 ( 546 noduri )este :

Graficul in QUICKFIELD 5.0 ( 343 noduri ) este :
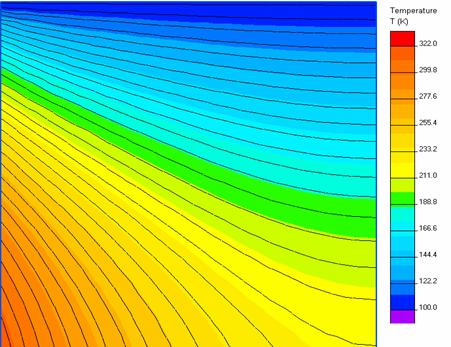
program lucrarea 6
c=================================================================
c------------REZOLVAREA ECUATIEI DE CONDUCTIE TERMICA 2D STATIONARA--
c (metoda volumelor finite)
c------------ECUATIA REZOLVATA:(divk(gradT))=0-------- ----- ------ -------------
c------------VARIABILELE DE INTRARE-------- ----- ------ ----- ----- ----- ----- ------
c NNX : numarul de noduri pe directia x
c NNY : numarul de noduri pe directia y
c L : lungimea domeniului de calcul
c H : inaltimea domeniului de calcul
c TB : conditia Dirichlet
c------------CONDITIILE LA LIMITA-------- ----- ------ ----- ----- --------- ----- ------
c Dirichlet la frontiera nord TB(x,H)=100
c Neumann (flux nul) la frontiera est si sud
c Flux impus (q) la frontiera vest
c------------VARIABILELE DE INTRARE-------- ----- ------ ----- ----- ----- ----- -----
c TEMP : temperatura T(x,y)
c------------AUTOR :Irimia Marius EG 11502
c=================================================================
parameter(nnx=21, nny=26, nit=25000)
double precision TEMP(nnx,nny),AX(nnx,nny),AY(nnx,nny)
double precision A(nnx,nny),B(nnx,nny),C(nnx,nny)
double precision wk(nnx,nny)
double precision A1(nny),B1(nny),C1(nny),wk1(nny),temp1(nny)
double precision DX,DY,TB,L,H,la,gz,q
data TB/100.0/,L/0.4/,H/0.5/,la/1000.0/,gz/0.01/
data q/500000.0/
c------------CALCULUL PASULUI SPATIULUI(DX)-------- ----- ------ -------------
DX=L/(nnx-1)
DY=L/(nny-1)
write(*,*)'DX=',dx
write(*,*)'DY=',dy
c------------INITIALIZAREA TEMPERATURII-------- ----- ------ ----- ----- ---------
do i=1,nnx
do j=1,nny
TEMP(i,j)=0.0
enddo
enddo
c-----------INITIALIZAREA CONDITIILOR LA LIMITA DE TIP DIRICHLET----- ----- ----
c----- ----- -------------LA FRONTIERA NORD-------- ----- ------ ----- ----- ------------
do i=1,nnx
TEMP(i,nny)=TB
enddo
c----- ----- ------------BUCLA DE ITERATIE-------- ----- ------ ----- ----- ----- ----- ----
do k=1,nit
c------------FORMAREA VECTORILOR DIAGONALELOR-------- ----- ------ ---
do i=1,nnx-1
if(i.eq.1)then
c------------DIAGONALA INFERIOARA-------- ----- ------ ----- ----- ----- ----- ------
do j=1,nny-1
if(j.eq.1)then
A(i,j)=0.0
A1(j)=A(i,j)
else
A(i,j)=-la*(DX/2.0*gz)/DY
A1(j)=A(i,j)
endif
enddo
c------------DIAGONALA SUPERIOARA-------- ----- ------ ----- ----- ----- ----- ------
do j=1,nny-2
if(j.eq.1)then
C(i,j)=-la*(DX/2.0*gz)/DY
C1(j)=C(i,j)
else
C(i,j)=-la*(DX/2.0*gz)/DY
C1(j)=C(i,j)
endif
enddo
C(i,nny-1)=0.0
C1(nny-1)=C(i,nny-1)
c------------DIAGONALA PRINCIPALA-------- ----- ------ ----- ----- --------- ----- -----
do j=1,nny-1
if(j.eq.1)then
B(i,j)=la*(DY/2.0*gz)/DX+la*(DX/2.0*gz)/DY
B1(j)=B(i,j)
else
B(i,j)=la*(DY*gz)/DX+la*(DX/2.0*gz)/DY+la*(DX/2.0*gz)/DY
B1(j)=B(i,j)
endif
enddo
c------------FORMAREA INITIALA A TERMENULUI LIBER WK----- ----- --------- ----- -----
do j=1,nny-2
if(j.eq.1)then
wk(i,j)=(la*(DY/2.0*gz)/DX)*TEMP(i+1,j)+DY/2.0*gz*q
wk1(j)=wk(i,j)
else
wk(i,j)=(la*(DY*gz)/DX)*TEMP(i+1,j)+DY*gz*q
wk1(j)=wk(i,j)
endif
enddo
wk(i,nny-1)=(la*(DY*gz)/DX)*TEMP(i+1,nny-1)+DY*gz*q+
* (la*(DX/2.0*gz)/DY)*TEMP(i,nny)
wk1(nny-1)=wk(i,nny-1)
c-----------REZOLVAREA SISTEMULUI-------- ----- ------ ----- ----- ----- ----- -------
CALL TRIDAG(a1,b1,c1,wk1,temp1,nny-1)
c-FORMAREA SOLUTIEI PE TOATA LINIA VERTICALA(LINIA APLICARII TDMA)-
do j=1,nny-1
TEMP(i,j)=temp1(j)
enddo
else
c------------DIAGONALA INFERIOARA-------- ----- ------ ----- ----- --------- ----- ----
do j=1,nny-1
if(j.eq.1)then
A(i,j)=0.0
A1(j)=A(i,j)
else
A(i,j)=-la*(DX*gz)/DY
A1(j)=A(i,j)
endif
enddo
c------------DIAGONALA SUPERIOARA-------- ----- ------ ----- ----- ----- ----- -------
do j=1,nny-2
if(j.eq.1)then
C(i,j)=-la*(DX*gz)/DY
C1(j)=C(i,j)
else
C(i,j)=-la*(DX*gz)/DY
C1(j)=C(i,j)
endif
enddo
C(i,nny-1)=0.0
C1(nny-1)=C(i,nny-1)
c------------DIAGONALA PRINCIPALA-------- ----- ------ ----- ----- --------- ----- ----
do j=1,nny-1
if(j.eq.1)then
B(i,j)=la*(DY/2.0*gz)/DX+la*(DY/2.0*gz)/DX+la*(DX*gz)/DY
B1(j)=B(i,j)
else
B(i,j)=la*(DY*gz)/DX+la*(DY*gz)/DX+la*(DX*gz)/DY+la*(DX*gz)/DY
B1(j)=B(i,j)
endif
enddo
c------------FORMAREA INITIALA A TERMENULUI LIBER WK----- ----- --------- ----- -----
do j=1,nny-2
if(j.eq.1)then
wk(i,j)=(la*(DY/2.0*gz)/DX)*TEMP(i-1,j)+
(la*(DY/2.0*gz)/DX)*TEMP(i+1,j)
wk1(j)=wk(i,j)
else
wk(i,j)=(la*(DY*gz)/DX)*TEMP(i-1,j)+(la*(DY*gz)/DX)*TEMP(i+1,j)
wk1(j)=wk(i,j)
endif
enddo
wk(i,nny-1)=(la*(DY*gz)/DX)*TEMP(i-1,nny-1)+
* (la*(DY*gz)/DX)*TEMP(i+1,nny-1)+(la*(DX*gz)/DY)*TEMP(i,nny)
wk1(nny-1)=wk(i,nny-1)
c-----------REZOLVAREA SISTEMULUI-------- ----- ------ ----- ----- -----
CALL TRIDAG(a1,b1,c1,wk1,temp1,nny-1)
c----- ----- ----FORMAREA SOLUTIEI PE TOATA LINIA VERTICALA----- ----- ------------
do j=1,nny-1
TEMP(i,j)=temp1(j)
enddo
endif
enddo
c===========================PENTRU i=nnx==========================
c------------DIAGONALA INFERIOARA-------- ----- ------ ----- ----- ----- ----- -------
do j=1,nny-1
if(j.eq.1)then
A(nnx,j)=0.0
A1(j)=A(nnx,j)
else
A(nnx,j)=-la*(DX/2.0*gz)/DY
A1(j)=A(nnx,j)
endif
enddo
c------------DIAGONALA SUPERIOARA-------- ----- ------ ----- ----- ----- ----- -------
do j=1,nny-2
if(j.eq.1)then
C(nnx,j)=-la*(DX/2.0*gz)/DY
C1(j)=C(nnx,j)
else
C(nnx,j)=-la*(DX/2.0*gz)/DY
C1(j)=C(nnx,j)
endif
enddo
C(nnx,nny-1)=0.0
C1(nny-1)=C(nnx,nny-1)
c------------DIAGONALA PRINCIPALA-------- ----- ------ ----- ----- --------- ----- ----
do j=1,nny-1
if(j.eq.1)then
B(nnx,j)=la*(DY/2.0*gz)/DX+la*(DX/2.0*gz)/DY
B1(j)=B(nnx,j)
else
B(nnx,j)=la*(DY*gz)/DX+la*(DX/2.0*gz)/DY+la*(DX/2.0*gz)/DY
B1(j)=B(nnx,j)
endif
enddo
c------------FORMAREA INITIALA A TERMENULUI LIBER WK----- ----- --------- ----- -----
do j=1,nny-2
if(j.eq.1)then
wk(nnx,j)=(la*(DY/2.0*gz)/DX)*TEMP(nnx-1,j)+DY/2.0*gz*q
wk1(j)=wk(nnx,j)
else
wk(nnx,j)=(la*(DY*gz)/DX)*TEMP(nnx-1,j)
wk1(j)=wk(nnx,j)
endif
enddo
wk(nnx,nny-1)=(la*(DY*gz)/DX)*TEMP(nnx-1,nny-1)+DY*gz*q+
(la*(DY/2.0*gz)/DY)*TEMP(nnx,nny)
wk1(nny-1)=wk(nnx,nny-1)
c-----------REZOLVAREA SISTEMULUI-------- ----- ------ ----- ----- ----- ----- -------
CALL TRIDAG(a1,b1,c1,wk1,temp1,nny-1)
c----- ----- ----FORMAREA SOLUTIEI PE TOATA LINIA VERTICALA----- ----- -------------
do j=1,nny-1
TEMP(i,j)=temp1(j)
enddo
enddo
c----FORMAREA VECTORULUI PENTRU PUNCTELE DE CALCUL PE X SI PE Y-----
AX(1,1)=0.0
AY(1,1)=0.0
do i=1,nnx
do j=2,nny
AY(i,j)=AY(i,j-1)+DY
enddo
enddo
do j=1,nny
do i=2,nnx
AX(i,j)=AX(i-1,j)+DX
enddo
enddo
c-----------SCRIEREA SOLUTIEI-------- ----- ------ -------- ----- ------ ----
open(20,file='apl5.prn')
do i=1,nnx
write(20,101)(TEMP(i,j),j=1,nny)
enddo
close(20)
101 format(26(1x,f6.2))
stop
end
subroutine tridag(a,b,c,r,u,n)
parameter (NMAX=200000)
integer j
double precision a(n),b(n),c(n),r(n),u(n)
double precision bet, gam(NMAX)
c----------a=diagonala inferioara-------- ----- ------ -------- ----- ------ -------
c----------b=diagonala principala-------- ----- ------ -------- ----- ------ -------
c----------c=diagonala superioara-------- ----- ------ -------- ----- ------ ------
c----------r=termenul din partea dreapta-------- ----- ------ ----- ----- --------- ----- -------
c----------u=termenul necunoscut-------- ----- ------ -------- ----- ------ ------
c----------n=dimensiunea sistemului-------- ----- ------ -------- ----- ------ ---
c----------NMAX=numarul maxim al ecuatiei-------- ----- ------ ----- ----- ----- ----- ----
if (b(1).eq.0) pause 'tridag:rewrite equations !'
bet=b(1)
u(1)=r(1)/bet
do j=2,n
gam(j)=c(j-1)/bet
bet=b(j)-a(j)*gam(j)
if(bet.eq.0) pause 'tridag failed'
u(j)=(r(j)-a(j)*u(j-1))/bet
enddo
do j=n-1,1,-1
u(j)=u(j)-gam(j+1)*u(j+1)
enddo
return
end
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1958
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved