| CATEGORII DOCUMENTE |
| Animale | Arta cultura | Divertisment | Film | Jurnalism | Muzica |
| Pescuit | Pictura | Versuri |
Capitolul 1
Introducere
De la regulatorul centrifugal watt reprezentat in figura 1.1 conceput pentru a controla viteza motoarelor cu abur,metodologiile de control ale sistemului au evoluat de la simple structuri mecanice cu feedback, in dispozitive electronice avansate si sofisticate pentru a controla sistemele instabile de inalta performanta cu o mai buna optimizare a costului si a controlului. In ultimele 5 decenii au aparut mai multe metode de control pentru a creste performantele si stabilitatea in conditii de zgomot si perturbatii.Unele dintre aceste legi de control, de exemplu legea P.I.D. si filtrele kalman sunt folosite cu success in industrie avand o gama larga de aplicabilitate.
Fig 1.1:controller centrifugal watt
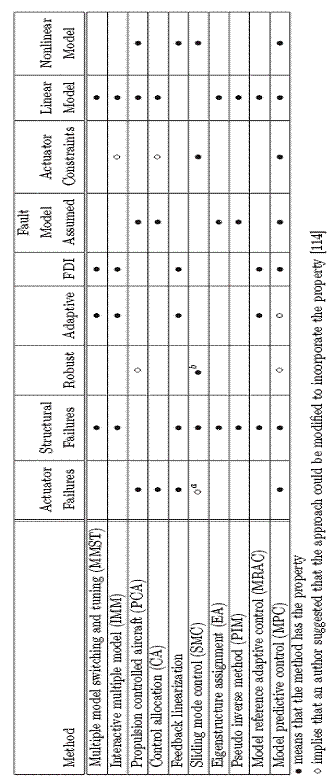
Unele dintre metodele de control care au beneficiat de o atentie deosebita in ultimele decenii sunt metode robuste si metode de control adaptiv. Acest lucru este motivat de necesitatea de a optimiza performantele sistemelor critice de siguranta. La aparitia anumitor evenimente neobisnuite in sistem acesta este "suparasolicitat" si isi poate pierde stabilitatea. Exemple ale unor evenimente neasteptate sunt defectarea sau avarierea sistemelor care nu sunt luate in considerare in proiectarea sistemelor de control. Problema obtinerii unui nivel de performanta si stabilitate optima in cazul aparitiei acestor evenimente neprevazute, in special pentru sistemele critice de siguranta, si sistemele automate costisitoare necesita o strategie de control diferita nu doar sa aiba un contol adaptive robust. Un exemplu de astfel de sistem care necesita o asemenea modalitate de control este problema cresterii sanselor, avionului sa nu se prabuseasca la aparitia unor defectiuni. Intr-o asemenea situatie avionul necesita o strategie de urgenta pentru a-i permite pilotului aterizarea avionului in siguranta. Aceasta provocare a motivat aparitia unei strategii de control cunoscuta in literatura de specialitate sub numele de FTC ( Fault Tolerant Control ). Multe paradigme diferite au fost aplicate problemei FTC. Exemple ale unor abordari de control exixtente pot fi gasite in tabelul 1.1.Tabelul 1.2 prezinta diferite sisteme carora li s-a aplicat FTC. In aceasta lucrare vor fi demonstrate avantajele folosirii FTC pe diferite sisteme de avionica.
1.1.Avantaje ale sistemelor de detectie a erorilor
Siguranta avioanelor de pasageri a fost si continua sa fie o problema importanta in industria aeronautica. Figurile 1.2 si 1.3 reprezinta statistici recente referitoare la siguranta avioanelor civile. Desi s-a dublat numarul de zboruri incepand din 1980, numarul accidentelor fatale s-a mentinut de-a lungul timpului la aceeasi valoare, ba chiar a scazut in perioada 1999 - 2003. Aceasta a fost contributia mai multor factori cum ar fi masurile de siguranta impuse avioanelor si implementarea unor tehnologii de varf.
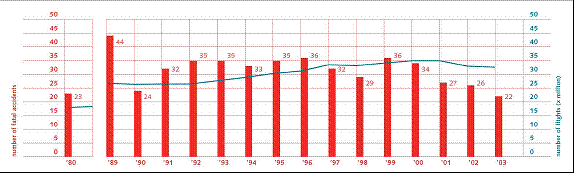
Fig 1.2 Numarul zborurilor si al accidentelor fatale
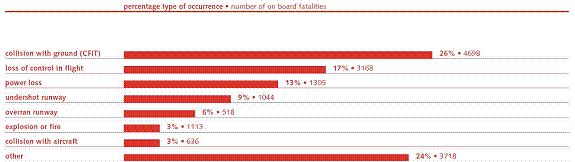
Fig 1.3 Tipuri de defecte
Figura 1.3 prezinta "controlul zborului la sol"( CFIT ) si "pierderea controlului in aer"acestea fiind doua dintre cele mai importante evenimente care duc la paritia accidentelor fatale. Pierderea controlului in timpul zborului este unul dintre factorii care au dus la aparitia FTC : ideea fiind cresterea fiabilitatii avionului la aparitia unor defecte. S-a argumentat faptul ca un pilot bine pregtit si un FTC pot evita aparitia mai multor accidente. De exemplu un raport recent descrie un experiment al NASA in care din cauza pierderii sistemului hidraulic avionul poate fi adus in siguranta la sol folosind doar motoarele. Dupa zbor s-a dovedit faptul ca avionul dotat cu FTC este mult mai controlabil decat cel fara FTC. Desi munca facuta de NASA asupra avionul controlat numai cu ajutorul sistemului de propulsie dupa pierderea sistemului hidraulic, aceasta nu este suficienta sa resolve problema generala a FTC pentru avioane; in special cand alte suprafete de control sunt functionale, sau cand avem de-a face cu distrugerea structurii, sau blocarea suprafetelor de comanda sau a trenului de aterizare.
Unul dintre obiectivele acestei lucrari este obtinerea unei stabilitati si recuperarea din performantele pierdute ale avionului la aparitia unui defect.
1.2. Provocari in domeniul FTC si FDI
Evolutiilor recente in domeniul FTC si FDI (Fault Detection and Isolation) le-au fost implementate idei ale modului de alunecare. Aceasta se datoreaza proprietatilor robuste inerente ale modurilor de alunecare, inclusiv capacitatea sa de a face fata direct defectelor actuatorului fara a fi necesara detectarea defectiuni si fara a fi necesara reconfigurarea controlerului. In ciuda proprietatilor robuste care ii permit sa faca fata defectarii actuatorului, SMC (Sliding Mode Control) nu poate suporta defectarea totala a acestuia. Unele cercetari recente au dovedit ca se poate simula defectarea actuatorului, dar nu se poate aplica decat catorva sisteme de punere in miscare. In cele mai multe sisteme de punere in miscare, cum ar fi avioanele mari de transport, redundanta actuatorului este disponibila dar de cele mai multe ori nu in forma de simulare exacta a actuatoarelor primare ale suparafetelor de control. Prin urmare, provocarea este de a gasi o modalitae ca modurile de alunecare sa faca fata defectarii totale a actuatorului.
Exista foarte putine informatii in literatura de specialitate despre aplicatiile SMC in sistemele de avionica. Majoritatea aplicatiilor SMC pot fi gasite la avioane de inalta performanta; de exemplu avioanele fara ampenaj. Este foarte greu da gasit informatii despre SMC folosite in avioanele mari de transport - in special in scopul folosirii FTC. Unul dintre motive este probabil scepticismul inginerilor cu privire la problemele de "chattering" asociate cu o miscare de alunecare ideala si "mitul" conform caruia SMC necesita computere performante pentru a fi implementate in avioanele reale.
Provocarea este sa se denonstreze ca SMC este un instrument puternic in gestionarea defectelor care pot aparea in sistemele aeronavelor.
Un motiv pentru care este folosit ca exemplu in aceasta lucrare un avion de transport mare, este disponibilitatea modelului FTLAB747, care este unul dintre modelele matematice precise al unui avion, cu coeficienti aerodinamici obtinuti de NASA in timpul zborului si in tunelul aerodinamic. Desi exista modele cum ar fi ADMIRE care cuprind ecuatii neliniare, FTLAB747 este singurul model care reproduce conditiile unui defect real.
Capitolul 2
Detectia, controlul si izolarea defectelor
Cand in sistem apare o defectiune, problema principala este sa determinam ce fel de defect este si sa decidem cum actionam. Problema detectarii unui defect este gasirea sursei si apoi sa luam masuri corespunzatoare. In acest capitol va fi prezentata o discutie despre FTC si FDI. In acest capitol se va pune accent pe aplicatiile FTC si FDI in aeronautica.
2.1 Defecte si Erori
La inceput trebuie sa definim acesti termeni. Definitiile date in aceasta teza sunt in concordanta cu definitiile date de comitetul tehnic IFAC SAFEPROCES care au fost date pentru a stabili un standard in acest domeniu si pentru a evita confuziile in randul cercetatorilor.
Definitie
Eroare - o schimbare nedorita in parametrii sistemului care duce la micsorarea performantelor.
Defect - distrugerea integrala sau partiala a unei componente sau fuctii.
2.1.2 Tipuri de defecte si erori
Defectarea unui actuator este definita in literatura de specialitate ca o scadere a eficientei actuatorului. Defectele care apar intr-un sistem liniar asociate cu actuatoarele pot fi reprezentate de ecuatia:
![]() (2.1)
(2.1)
unde ![]() si
si ![]() unde
unde ![]() sunt scalari care satisfac conditia
sunt scalari care satisfac conditia ![]() Acest model scalar scade eficienta unui actuator. Daca
Acest model scalar scade eficienta unui actuator. Daca
![]() atunci actuatorul functioneaza perfect, daca
atunci actuatorul functioneaza perfect, daca ![]() actuatorul are erori, daca
actuatorul are erori, daca ![]() actuatorul este defect in totalitate.
actuatorul este defect in totalitate.
Observatie
Reprezentarea
erorilor/defectelor in ecuatia (2.1) reprezinta reducerea eficacitatii unui
actuator particular prin structura diagonala a lui ![]() .
Reprezentarea erorilor/defectelor ca in ecuatia (2.1) face ca analiza
stabilitatii si integrarea FDI sa fie mai simpla. Defectele actuatorului sunt cel
mai adesea luate in considerate de proiectantii FTC.
.
Reprezentarea erorilor/defectelor ca in ecuatia (2.1) face ca analiza
stabilitatii si integrarea FDI sa fie mai simpla. Defectele actuatorului sunt cel
mai adesea luate in considerate de proiectantii FTC.
In termenii
sistemului de control liniar descris de ecuatia (2.1) acesta afecteaza numai
matricea ![]() a sitemului liniar. Alt tip de defect care apare
la avion este distrugerea structurii fuselajului. Distrugerea structurii poate
cauza schimbarea conditiilor de operare ale avionului datorita schimbarii
coeficientilor aerodinamici sau a miscarii centrului de greutate. Matricea
a sitemului liniar. Alt tip de defect care apare
la avion este distrugerea structurii fuselajului. Distrugerea structurii poate
cauza schimbarea conditiilor de operare ale avionului datorita schimbarii
coeficientilor aerodinamici sau a miscarii centrului de greutate. Matricea ![]() poate fi si ea perturbata. Reprezentarea
matematica va fi urmatoarea:
poate fi si ea perturbata. Reprezentarea
matematica va fi urmatoarea:
![]() (2.2)
(2.2)
unde
![]() si
si ![]() reprezinta schimbarile aparute in sistem in
matricele
reprezinta schimbarile aparute in sistem in
matricele ![]() si
si ![]() ,
, ![]() reprezinta schimbarile aditionale neincluse in
reprezinta schimbarile aditionale neincluse in
![]() si
si ![]() aparute datorita unor nepotriviri inte
sistemul nominal si sistemul defect.
aparute datorita unor nepotriviri inte
sistemul nominal si sistemul defect.
Biasul
este o eroare
Eroarea
de drift a senzorilor este o conditie unde eroarea masurata creste in timp si
este datorata pierderii sensibilitatii. Pierderea acuratetii are loc atunci
cand masurarea nu reflecta adevarata valoare de stare. Blocarea semnalelor
senzorului indica faptul ca senzorul ofera o valoare
Defectele pot fi impartite in functie de modul de aparitie: bruste sau lente. Defectele bruste au o neastepata schimbare si sunt usor de sesizat de catre pilot. Un exemplu concludent este blocarea actuatorului. Defectele lente sunt mai subtile si greu de observat. Totusi daca defectele lente nu sunt remediate intr-o anumita perioada de timp pot duce la un defect catastrofal.
2.2 FTC. Generalitati
In literatura de specialitate, munca de cercetare in FTC include rezolvarea problemelor intalnite in sisteme de siguranta critice cum ar fi avioanele. Aplicatiile se gasesc si in alte sisteme, de exemplu roboti, sisteme spatiale, si submarine teleghidate.
FTC este o combinatie complexa intre trei domenii de cercetare: FDI, control robust si control reconfigurabil. Ca un rezumat in figura 2.2 sunt aratate interconexiunile dintre cele trei domenii. Pentru o schema tipica FTC cand apare un defect fie in actuator fie in sensor, sistemul FDI v-a detecta si localiza sursa defectului. Aceasta informatie este apoi transmisa unui mecanism pentru a initia reconfigurarea. Controlerul reconfigurat v-a incerca sa se adapteze defectului, deci v-a furniza stabilitate si un anumit nivel de performanta.
Controlul robust este in stransa legatura cu FTC
pasiv (PFTCS). Controlerul este proiectat sa faca fata perturbatiilor in timpul
proiectarii. Controlerul trebuie sa
gestioneze defectul fara a fi necesara reconfigurarea sa sau FDI. Pentru unele metodologii
capacitatea de gestionare a defectului este limitata si defectarea totala a
actuatorului nu v-a putea fi gestionata direct. Un exemplu de o astfel de
strategie este ![]() unde defectul incertitudinii este minimalizat
in timpul proiectarii.
unde defectul incertitudinii este minimalizat
in timpul proiectarii.
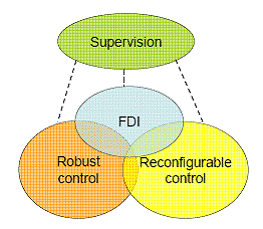
Fig 2.1
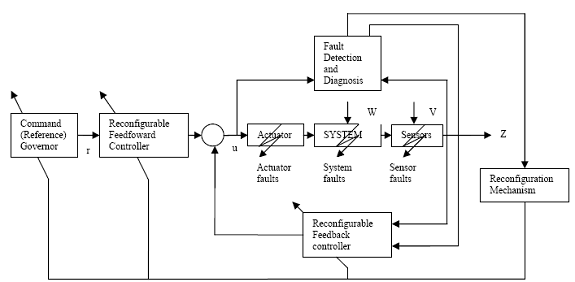
Fig 2.2
FTC se clasifica in doua mari grupe:
PFTCS - FTC pasive
AFTCS - FTC active
In PFTCS controlerul este proiectat sa fie intolerant cu erorile si incertitudinile. De aceea cand apar erori controlerul ar trebui sa fie capabil sa mentina stabilitatea sistemului cu o acceptabila scadere a performantei. PFTCS nu necesita FDI si nici controler reconfigurabil sau adaptiv.
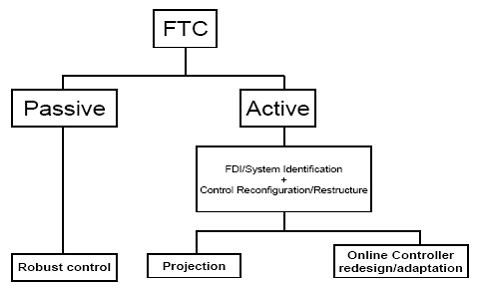
Fig 2.3
AFTCS pe de alta parte, reactioneaza la defectarea componentelor sistemului intr-un mod activ reconfigurand actiunile de control astfel incat stabilitatea si performantele intregului sistem sa fie mentinute. De aceea cele mai multe AFTCS au nevoie de FDI pentru a furniza informatii despre defectiuni astfel incat sa fie facuta reconfigurarea.
2.3 Criterii pentru FTC: Redundanta
Unul dintre factorii principali care permit aterizarea in siguranta dupa aparitia unui defect este manipularea inteligenta a suprafetelor de control redundante pentru a obtine un nivel de performanta dorit. In cazul unei urgente cauzate de un defect, pilotii vor folosi resursele disponibile pentru a ateriza in siguranta. Redundanta poate fi clasificata in:
redundanta directa
redundanta analitica
In cazul redundantei directe hardware-ul fizic al redundantei este disponibil.
In ceea ce priveste redundanta senzorilor; daca exista trei senzori care masoara eceeasi stare, redundanta se numeste dubla sau tripla. In operatiunile normale un singur sensor este suficient, totusi doi sau trei senzori sunt necesari pentru a asigura o masurare corecta in cazul aparitiei unui defect. Sistemul de vot este o cale tipica pentru a decide care canale functioneaza corect si care nu functioneaza. Acest concept de redundanta hardware poate fi de asemenea extins si la actuatoare. In ceea ce priveste redundanta analitica, in loc sa avem doi sau trei senzori care masoara acelasi semnal, un observer, care asigura o estimare a semnalelor de interes, asigura redundanta analitica. Nu exista nici un hardware implementat, dar exista anumiti algoritmi sau modele matematice sau observere care ruleaza in computerul de bord. Aceasta este de dorit in multe sisteme in special in avioane sau UAV-uri deoarece redundanta analitica elimia din numarul echipamentelor deci reduce greutatea si costul. Dezvoltarea sistemelor de siguranta critice cum ar fi vehicule de reintrare in atmosfera dau posibilitatea construirii redundantei inca din timpul proiectarii. Pentru multe sisteme provocarea este sa foloseasca senzorii si actuatoarele existente pentru a face fata defectelor. In avioanele mari de transport redundanta este deja disponibila. Chiar si asa, aceasta nu este prevazuta pentru FTC, iar existenta suprafetelor de control suplimentare, da posibilitatea folosirii lor pentru a obtine acelasi efect ca folosirea suprafetelor de control originale.
In avioanele de transport de pasageri senzorii au de obicei tripla redundanta.
La avioane suprafata de control, de exemplu directia poate avea trei actuatoare hidraulice diferite functionand pe trei linii separate cu trei pompe hidraulice independente. Aceasta inseamna ca cele mai multe suprafete de control vor avea redundanta tripla. In avioanele de transport mari, spoilerele care de obicei sunt folosite pentru reducerea vitezei pot fi folosite in mod diferential pentru a crea ruliu care in mod normal e obtinut prin folosirea eleroanelor. Deasemenea motoarele pot fi folosite pentru a crea giratie, care e obtinuta prin folosirea directiei; si in final stabilizatorul orizontal, care e folosit pentru stabilirea unghiului de atac, poate inlocui profundorul pentru miscarea longitudinala.
2.4 Obtinerea tolerantei la erori
In aceasta teza figura 2.4 prezinta o modul in care se obtine FTC. FTC pasiv se bazeaza de obicei pe idei de control robuste si de aceea face fata erorilor/defectelor fara a fi nevoie de alte informatii de la sistemul FDI.
FTC activ (AFTC) in general are nevoie de informatii despre erorile/defectele din sistem si de aceea are nevoie de FDI. AFTC poate fi clasificat in doua subgrupe:
FTC proiectat
FTC cu reconfigurare online
In sisteme FTC care se bazeaza pe proiectare controlerul e folosit pentru toate defectele care pot aparea in sistem. Controlerul proiectat va fi activat numai cand apare un anumit tip de defect.
AFTC se bazeaza pe reconfigurarea sau adaptarea online. Aici au fost propuse inca doua subcomponente:
FTC care este obtinut printr-un control adaptiv;
FTC care poate fi obtinut prin redistribuirea semnalelor de control.
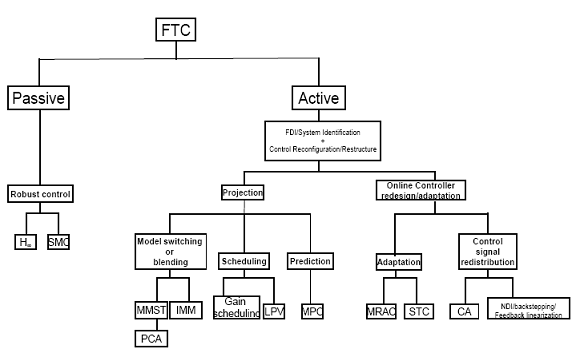
Fig 2.4
2.4.1 Adaptarea
Un mod de a face fata schimbarilor din sistem este
adaptarea controlerului. Bazata pe proiectarea pilotilor automati pentru
avioane de inalta performanta in anii '50 controlul adaptiv a fost propus ca un
mod de a face fata unei game largi de conditii de zbor. Controlul adaptiv este
folosit pentru ajustarea automata a parametrilor controlerului pentru a obtine
performantele dorite. Exista doua metode de control adaptiv care sunt adaptarea
directa si indirecta. In adaptarea indirecta sunt doua etape de proiectare a
controlerului. Prima data este necesara
estimarea parametrilor sistemului. In cazul sistemelor liniare perechea de
matrici ![]() trebuie estimata in functie de schimbarile
care apar in conditiile de operare. Etapa urmatoare in adaptarea indirecta e
folosirea acestor informatii in proiectarea controlerului. In metoda adaptarii
directe controlerul e proiectat direct fara estimarea parametrilor sistemului.
Un exemplu de controler proiectat cu control adaptiv este modelul MRAC (Model
Reference Adaptive Control) si STC (Self Tuning Control). In MRAC parametrii necunoscuti nu
sunt perfect estimati, ci mai degraba
sunt ajustati incat iesirea sistemului sa urmeze performantele dorite ale
buclei in circuit inchis facand ca
erorile de urmarire sa tinda la zero. Figurile 2.5 si 2.6 arata diferentele in
structura MRAC si STC.
trebuie estimata in functie de schimbarile
care apar in conditiile de operare. Etapa urmatoare in adaptarea indirecta e
folosirea acestor informatii in proiectarea controlerului. In metoda adaptarii
directe controlerul e proiectat direct fara estimarea parametrilor sistemului.
Un exemplu de controler proiectat cu control adaptiv este modelul MRAC (Model
Reference Adaptive Control) si STC (Self Tuning Control). In MRAC parametrii necunoscuti nu
sunt perfect estimati, ci mai degraba
sunt ajustati incat iesirea sistemului sa urmeze performantele dorite ale
buclei in circuit inchis facand ca
erorile de urmarire sa tinda la zero. Figurile 2.5 si 2.6 arata diferentele in
structura MRAC si STC.
Idea modificarii unui controler este foarte folosita in special atunci cand nu este necesara schimbarea structurii controlerului. Aceasta este intr-adevar una dintre componentele unui model multiplu de control reglabil (MMST). In MMST cand sistemul este la o conditie de operare, un model predefinit si un controler vor fi alese si structura controlerului va ramane neschimbata in apropierea acelei conditii de operare. In acest timp reglarea parametrilor controlerului poate ajuta la obtinerea unor performante mai bune comparabile cu cele ale unui controler fix. In MRAC idea este folosirea modelului clasic si combinarea lui cu un sistem adaptiv astfel incat sistemul sa aiba capabilitatea de a face fata schimbarilor din sistem.
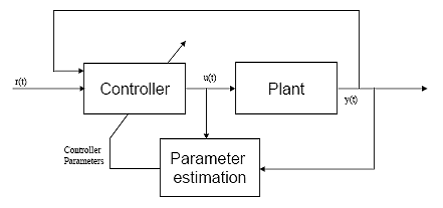
Fig 2.5
Figura 2.6 prezinta o structura tipica pentru MRAC. Contine modelul de referinta, legea de reglare si controlerul adaptiv.
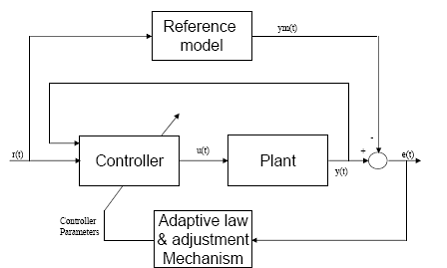
Fig 2.6
Sistemul trebuie sa aiba o structura fixa dar parametrii sunt necunoscuti. Modelul de referinta este tipic pentru raspunsul buclei inchise la semnalele de comanda externe. Majoritatea performantelor specificate sunt date in domeniul timp, de exemplu timpul de crestere, raportul de amortizare. Acestea pot fi reprezentate intr-un raspuns ideal al functiei de transfer, care devine semnal de referinta in sistemul de urmarire al buclei inchise. Parametrizarea controlerului se face prin parametri ajustabili pentru a permite controlerului sa se adapteze la schimbarile sistemului si iesirea sa urmareasca raspunsul dorit.
O diferenta majora intre MMSI si IMM (Interacting Multiple Model) comparat cu MRAC este ca modelul de referinta asigura performantele dorite in bucla inchisa unde controlerul forteaza sistemul sa-l urmeze si ia semnalul de referinta de la intrare. In MMST si IMM, este folosit un ansamblu de modele in bucla deschisa. Sistemele MMST si IMM folosesc aceste modele in bucla deschisa pentru a identifica pe cea corecta care urmeaza sa fie folosita pentru conditiile de operare activand astfel controlerul predefinit. In general modelul schemei MRAC in bucla inchisa are o structura fixa cu parametri adaptivi.
Chiar daca exista posibiliatea schimbarii modelului de referinta si chiar controlerul, in fata unor distrugeri semnificative sau defecte mari, MRAC si STC singure nu au capabilitatea sa faca fata. De aceea o combinatie intre MRAC si STC cu alte metode de reconfigurare cum ar fi MMST si IMM trebuie sa faca fata schimbarilor majore din sistem. Aceste metode in controlul adaptiv pot fi gasite si in alte metode de control reconfigurabil si FTC.
2.4.2 Comutatia sau unirea
Idea folosirii unor modle multiple pentru controlul reconfigurabil a fost introdusa in anii '90. Aceste sisteme s-au dezvoltat deoarece este necesar sa se tina pasul cu schimbarile din sistem. Primele metode de control se bazau pe metode liniare si sistemele modelelor multiple pareau o idee buna pentru rezolvarea problemei schimbarii conditiilor de operare. La implementarea pe un sistem real, de obicei controlerele liniare trebuie sa se adapteze la conditiile de operare deoarece stabilitatea controlerului este garantata in apropierea conditiilor liniare. Folosirea acestor sisteme cu modele multiple este un mod de a se asigura ca controlerul poate fi proiectat astfel incat stabilitatea si performantele sa fie asigurate pentru o gama larga a anvelopei de zbor.
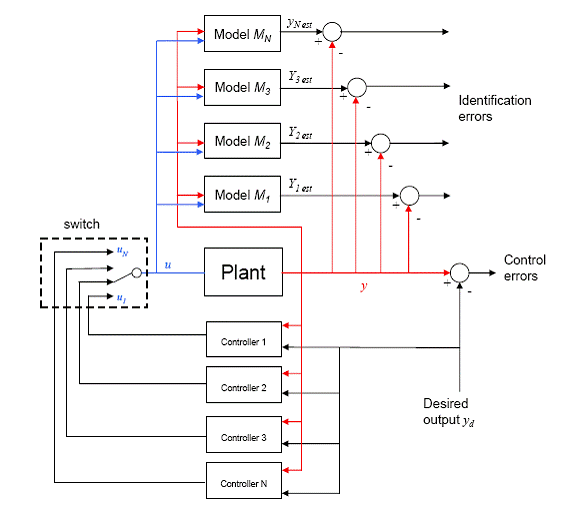
Fig 2.7
Din punctul de vedere al FTC, ansamblul de controlere se comporta ca un back-up si sunt activate numai cand apar erorile pentru care controlerul a fost proiectat. Aceasta metoda depinde de robustetea FDI pentru a furniza informatiile corecte despre tipul si locatia erorii/defectului pentru a permite controleului corect sa fie activat. Ansamblul de controlere trebuie sa contina toate erorile/defectele posibile. Un sistem FDI poate fi creat prin compararea starii curente a sistemului cu iesirile tuturor controlerelor din ansamblu. Aceasta lucrare vorbeste despre stabilitatea sistemelor de comutatie ca si despre performante in urma comutatiei. O modalitate de a proiecta un controler este sa folosim o imbunatatire a modelelor multiple si robuste. In figura 2.7 se arata ca pentru o conditie de operare un singur controler v-a fi ales in functie de eroarea dintre sistemul curent si modelul predefinit. Odata ce modelul si controlerul sunt alese, poate fi aleasa o metoda adaptiva pentru reglajul fin al controlerului.
Alte metode de control ca de exemplu MPC (Model Predictive Control) au fost luate in considerare pentru proiectarea controlerelor multiple. Avantajele acestei metode stau in aplicatii ale metodei de control liniar si in garantarea stabilitatii. Viteza detectarii erorilor este de asemenea mare. Desi aceasta metoda e bazata pe metode de control liniar, implementarea poate fi pretentioasa. Pentru a face fata tuturor tipurilor de defecte si erorilor inseamna ca numarul controlerelor care necesita sa fie proiectate si reglate este enorm. Comuatarea intre metode si controlere uneori introduce erori de tranzit neasteptate. De aceea uneori e nevoie de metode de transfer pentru a reduce efectul. Un alt dezavantaj este faptul ca anumite defecte nu pot fi prevazute. Un alt dezavantaj al acestei metode este dependenta de robustetea FDI pentru a identifica perechea corecta de modele si controlere care trebuie activate.
Avion controlat cu sistemul de propulsie (PCA):
o implementare de success a MMST in avionica
Incidental din Sioux City in 1999 si incidentul din Bagdad din 2004 demonstreaza recuperari remercabile ale controlului avionului folosind doar motoarele dupa pierderea sistemului hidraulic al suprafetelor de control. Un nefericit incident cu o defectiune similara a sistemului hidraulic a fost zborul 123 in Japonia 1984. Invatand din aceste incidente este evident ca folosind doar motoarele aterizarea poate fi posibila. Dupa incidentul din Sioux City NTSB a recommandat si incurajat dezvoltarea controlerelor de zbor cu backup sa fie folosite in situatii de urgenta .
Testele folosind sistemul PCA in varinata NASA Dryden au fost facute pe un avion real. Desi PCA le considera cele mai catastrofale defectiuni nu sunt suficiente pentru a rezolva problemele FTC. In cazul distrugeii aripii, pierderea motoarelor sau pierderea partiala a sistemului hidraulic PCA s-ar putea sa nu fie folositor.
IMM(Interacting Multiple Model)
Cu toate ca MMST poate fi folosit la rezolvarea problemei variatiei conditiilor de operare, in anumite cazuri este greu de obtinut un model liniar care se potriveste exact sistemului variabil. Ideea este obtinerea catorva modele liniare bazate pe cateva conditii de zbor atent alese si proiectarea controlerelor liniare multiple pentru aceste conditii de operare selectate. Cand conditiile de operare se schimba, iesirea estimata a unui sistem sau intrarea este obtinuta prin unirea modelelor predeterminate. Aceasta poate fi vazuta in figura 2.8.
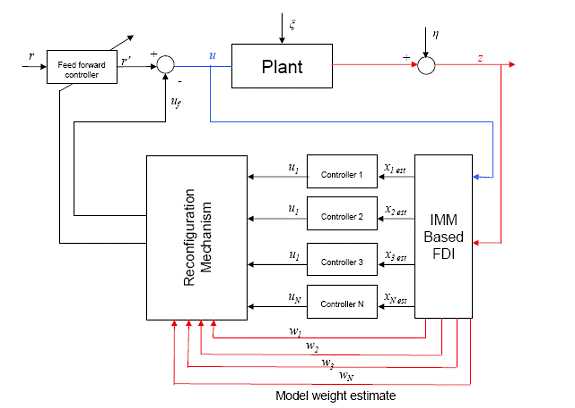
Fig 2.8
Strategia de control in sistemele IMM este ca estimatoarele sa dectecteze si sa izoleze eroarea/defectul obtinand o estimare a iesirii sistemului in urma unei insumari a unui model liniar predefinit care sa asigure o greutate probabila a controlerului reconfigurat. Principala presupunere folosita in IMM este aceea ca fiecare conditie de zbor posibila inclusiv defectele pot fi modelate ca o combinatie convexa a modelelor liniare predeterminate. Pasul al doilea este obtinerea semnalului de control bazat pe o amestecare a controlerelor predefinite s-au lege de control in timp real folosind greutatea probabila data de estimatorul IMM.
In prima etapa a sistemului IMM, s-a propus utilizarea unui ansamblu de filtre Kalman pentru a calcula probabilitatea unor defecte individuale. Aceasta probabilitate este de asemenea utilizata ca media ponderata a fiecarui model liniar predefinit pentru a estima starea sistemului.
In cel de-al doilea pas un ansamblu de controlere este proiectat bazat pe anticiparea defectelor care ar putea aparea. Ideea este ca in timpul defectelor valorile proprii ale sistemului in bucla inchisa trebuie sa tinda la valorile nominale fara conditii. Reconfigurarea controlerului vine de la utilizarea online a probabilitatii ca media ponderata sa determine combinarea raportului de control de intrare de la controlerul preproiectat in momentul in care defectul se produce.
Aceasta abordare este similara cu cea a sistemului MMST in sensul ca, daca defectele exacte sau anticipate apar, greutatea probabila v-a fi de unitate si restul de modele si controlere nu vor avea nici o contributie la estimarea starii si a semnalelor de intrare ale sistemului. In comparatie cu MMST, IMM are capacitatea de a face fata la defecte neanticipate. O problema a IMM este de a gasi echilibrul potrivit de combinare a greutatii probabile pentru a obtine cele mai bune modele potrivite. IMM este de asemenea puternic dependent de FDI pentru a identific in mod corect defectele.
2.4.3 PROGRAMAREA
Obtinerea programarii
Obtinerea programarii este legata de procedura de proiectare 'divide si cucereste'. Aceasta procedura are scopul de a rezolva problemele de control neliniar prin descompunerea sistemelor neliniare intr-o familie de sisteme liniare de proiectare a unui controler liniar pentru fiecare din ele. Pe baza acestei definitii MMST si IMM sunt tipuri particulare de programare. Termenul de obtinere a programarii se refera de asemenea la programarea modelelor liniare si controlerelor asociate fie prin paramatrii fie prin stare pentru a face fata problemelor controlului neliniar care rezulta din schimbarea conditiilor de operare si a anvelopei de zbor.
Un alt tip de obtinere a programarii este metoda de control (LPV) descrisa in subsectiunea urmatoare. Obtinerea programarii este de asemenea bazata pe precalcularea legilor de control. In anumite conditii de zbor nu este nevoie ca structura controlerului sa fie schimbata. Numai anumite controlere trebuie sa fie schimbate in functie de conditiile de zbor sau severitatea defectelor. Schimbarea nu se face adaptiv, in schimb gainurile predefinite sunt alese pentru anumite conditii de zbor specifice sau parametrii specifici. Acest lucru poate fi prezentat sub forma unui switch logic intre doua achizitii sau mai frecvent prin utilizarea unor tabele. Unul dintre avantajele obtinerii programarii este acela ca este usor de inteles si pus in aplicare. Cu toate acestea in unele cazuri defectele sunt atat de semnificative incat structura nominala a controlerelor nu face fata. In acest caz obtinerea programarii este insuficienta si este necesara reconfigurarea controlerului.
Variatia parametrilor liniari (LPV)
Controlul LPV este strans legat de obtinerea programarii. El este motivat de lipsa de performanta si stabilitate pentru obtinerea programarii. LPV este motivat de asemenea de o problema de proiectare si de a obtine mai multe modele si controlere lucru care este pretentios pentru o anvelopa de zbor mare.
Ideea in LPV
este de a obtine fara probleme modele semiliniare care pot varia sau pot fi
programate folosind un parametru ca altitudinea sau viteza astfel incat LPV sa
simuleze sistemul neliniar. Aici in loc de a alege o combinatie de modele
liniare predefinite, modelele schimba parametrii. Modelul LPV are structura
unui sistem liniar cu ![]() matrici dar fiecare matrice poate fi schimbata
pe baza unui parametru ales.
matrici dar fiecare matrice poate fi schimbata
pe baza unui parametru ales.
Un sistem LPV poate fi reprezentat de:
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
unde '![]() '
este un parametru variabil ex. viteza sau altitudinea. Daca
'
este un parametru variabil ex. viteza sau altitudinea. Daca ![]() =const. atunci LPV devine sistem
invariabil in timp (LTI).
=const. atunci LPV devine sistem
invariabil in timp (LTI).
Prima metoda de obtinere a LPV corespunde rearanjarii si transformarii sistemului neliniar intr-un sistem cvasi-LPV in cazul in care acesta are structura unui sistem liniar dar in cazul in care componentele matricelor variaza in functie de unele variabile comune. Cea de-a doua metoda se bazeaza pe metoda Jacobiana. Colectia modelelor liniare este parametrizata de una sau doua variabile asociate cu liniarizarea in jurul unui punct. Rezultatele sunt polinomiale si sunt continue pe tot parcursul conditiilor de zbor.
Dupa obtinerea modelelor LPV este proiectat si controlerul. In comparatie cu metodele clasice de programare in cazul in care gainurile sunt interpolari ale controlerului predefinit, controlerele LPV sunt dependente de schimbarea parametrilor sistemului.
Metodele Lyapunov au fost folosite pentru a proiecta controlere LPV. In domeniul FTC ideile LPV au fost folosite pentru a face fata cu defectele actuatorului. Observerele LPV au fost de asemenea luate in considerare pentru ca FDI sa genereze semnale reziduale pentru detectarea defectelor senzorilor actuatorului.
LPV ofera anumite garantii de stabilitate si performanta in comparatie cu obtinerea programarii clasice. Metodele de control neliniare pot fi folosite pentru a simplifica modelul LPV. Aceasta inseamna ca in comparatie cu metodele MMST si IMM controlerele nu trebuie sa fie proiectate pentru toate liniarizarile.
2.4.4 Prezicerea
Spre deosebire de multe alte paradigme de control care au venit din partea comunitati academice, dezvoltarea controlului predictiv MPC (Model Predictive Control) a fost initiata in industrie. Prin urmare nu este o surpriza faptul ca, MPC este cel mai utilizat pe scara larga si punerea in aplicare a metodei in procesul de control in industrie. Ideea originala pentru MPC este de a permite procesului de productie sa ruleze cat mai aproape de limitele procesului, fara a incalca aceasta limita si pentru maximizarea profitului. Principalul beneficiu al MPC este ca poate face fata limitelor si constrangerilor. Aceasta este principala motivatie pentru studiul MPC al zborului si pentru FTC. In timpul aparitiei defectelor in special la actuatoare, actuatoarele ramase vor fi conduse la limitele lor. Aici MPC are capacitatea de a gestiona actuatoarele inclusiv limitele acestora in procesul de optimizare, foarte dorit pentru obtinerea semnalelor de control. Daunele structurale pot fi deasemenea controlate in MPC prin modificarea modelului de referinta intern. In linii mari MPC este un algoritm de control iterativ bazat pe controlul optimal. Obiectivul este de a obtine prezicerea starilor viitoare, folosind starea curenta si calcularea semnalelor de control. Numai primul semnal de control, de la optimizare este aplicat actuatoarelor reale. Dupa aceea starile sunt prelevate din nou si calculate. Figura (2.9) ofera cateva introspectii in structura MPC.
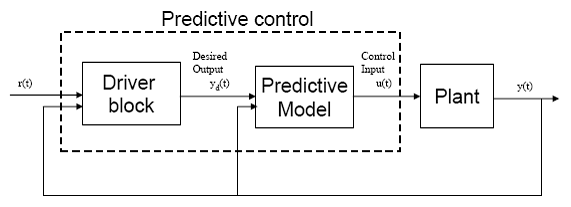
Fig. 2.9
Blocul conducator al modelului de referinta genereaza iesirile dorite bazate pe dinamica dorita. Modelul MPC genereaza semnale de control care forteaza iesirea sistemului sa urmeze iesirea dorita folosind intrarile si iesirile anterioare ale sistemului. Optimizarea poate fi rezolvata folosind programarea cuadrica sau algoritmi de programare liniara rapizi. MPC in forma sa cea mai puternica necesita o solutie online la problema constrangerilor optimizarii. Cu toate acestea in stadiul actual al tehnologiei, optimizarea online este inca greu realizabila pentru sistemele care necesita raspunsuri rapide. Ca si in cele mai multe strategii FTC, MPC este dependenta de FDI pentru a oferi informatii cu privire la erorile si defectele din sistem.
In cazul defectarii actuatorului comportamentul acestuia este nevoit sa apeleze la sistemul FDI astfel incat o noua constrangere sa poata fi inclusa in procesul de optimizare. In ceea ce priveste modificarea sistemului de control al zborului, mai exista o lipsa de indrumare in procesul de proiectare, care de obicei necesita incercari si erori de experienta.
Principalul beneficiu al MPC este ca pot face fata constrangerilor actuatoarelor si acest lucru a determinat studiul MPC in controlul zborului si FTC.
2.4.5 Redistribuirea semnalului de control
Metoda pseudo-inversa
Ideea metodei pseudo-inversa (PIM) este de a elabora un control astfel incat polii sistemului supus unei erori sau unui defect, vor fi cat mai aproape de valoarea nominala a polilor buclei inchise. Urmatoarele ecuatii ofera o introducere in metoda PIM. Se considera sistemul liniar :
![]() (2.5)
(2.5)
Presupunem ca o stare de feed-back K a fost proiectata si legea de control este:
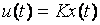 (2.6)
(2.6)
si deci sistemul in bucla inchisa este dat de
![]() (2.7)
(2.7)
In timpul defectelor, defectul sistemului in bucla inchisa poate fi reprezentat prin ecuatia
![]() (2.8)
(2.8)
Ideea este
de a obtine pe ![]() astfel incat performantele sistemului defect
in bucla inchisa vor fi cat mai apropiate de cele nominale ca in ecuatia (2.7).
astfel incat performantele sistemului defect
in bucla inchisa vor fi cat mai apropiate de cele nominale ca in ecuatia (2.7).
Avand in
vedere ca obiectivul este sa obtinem ![]() o conditie necesara este
o conditie necesara este
![]()
si prin urmare
![]()
in cazul in care![]() este pseudo-inversa a lui
este pseudo-inversa a lui ![]()
Matricele ![]() ale sistemului si
ale sistemului si ![]() se presupun a fi cunoscute. Defectele
sistemului
se presupun a fi cunoscute. Defectele
sistemului ![]() pot fi obtinute de la sistemul de identificare
online sau de la FDI ; atunci in principiu si
pot fi obtinute de la sistemul de identificare
online sau de la FDI ; atunci in principiu si ![]() poate fi obtinut online. Pentru o matrice non
patrata
poate fi obtinut online. Pentru o matrice non
patrata ![]() in PIM,
in PIM, ![]() ofera un oarecare grad de libertate.
ofera un oarecare grad de libertate.
Acest grad
de libertate de la ![]() a fost folosit pentru a redistribui comenzile
de control in scopul imbunatatirii sistemului in bucla inchisa. Chiar daca
conceptul de mai sus este usor si simplu de inteles, PIM are mai multe
dezavantaje care au impiedicat dezvoltarea lor suplimentara. Unul dintre
principalele dezavantaje este lipsa stabilitatii. Alte dezavantaje sunt
asociate cu presupunerea ca starea sistemului este in permanenta disponibila.
a fost folosit pentru a redistribui comenzile
de control in scopul imbunatatirii sistemului in bucla inchisa. Chiar daca
conceptul de mai sus este usor si simplu de inteles, PIM are mai multe
dezavantaje care au impiedicat dezvoltarea lor suplimentara. Unul dintre
principalele dezavantaje este lipsa stabilitatii. Alte dezavantaje sunt
asociate cu presupunerea ca starea sistemului este in permanenta disponibila.
In acelasi timp problema lipsei de robustete cand
perechea ![]() de la sistemul de identificare nu este perfect cunoscuta.
de la sistemul de identificare nu este perfect cunoscuta.
Conceptul de
modificare a PIM este discutabil. El se bazeaza pe o combinatie a PIM cu teoria
robustetei si stabilitatii sistemului cu structura incerta. Ansamblul de
matrici recalculate ![]() asigura un sistem stabil in bucla inchisa
pentru toate defectele posibile. El este de asemenea interesant pentru a
sublinia asemanarea intre abordarea PIM si urmatoarele metode in cazul in care sistemul in bucla-inchisa
este obligat sa urmeze bucla inchisa dorita in domeniul dinamic.
asigura un sistem stabil in bucla inchisa
pentru toate defectele posibile. El este de asemenea interesant pentru a
sublinia asemanarea intre abordarea PIM si urmatoarele metode in cazul in care sistemul in bucla-inchisa
este obligat sa urmeze bucla inchisa dorita in domeniul dinamic.
Alocarea controlului
La inceputul
dezvoltarii, ideea redistribuirii semnalelor de control catre actuatoarele
ramase functional s-a numit restructurare. Un exemplu este restructurarea
controlului utilizand conceptul de 'control combinat' folosit pentru
redistribuirea semnalelor de control. Datorita unor dezavantaje controlerul cu
restructurare nu a fost exploata in anii '90. Ideea a reaparut in ultimii ani
ca alocare partiala de control datorita dezvoltarii aeronavelor de inalta
performanta. Alocarea de control (CA) are capacitatea de a redistribui
semnalele de comanda de control la actuatoare in special in timpul defectelor.
Chiar daca PIM si CA par sa fie identice
in sensul ca ambele folosesc o pseudo-inversa care asigura un oarecare grad de
libertate la priectare, o mare diferenta intre CA si PIM este faptul ca in CA
operatorul este proiectat pe baza unui 'control virtual' al semnalului.
Avantajul este ca designul controlerului este independent de unitatea CA. Prin urmare CA poate fi
folosit in combinatie cu orice alt controler cum ar fi LQR sau ![]()
Fig 2.10
CA are capacitatea de a gestiona redundanta actuatorului care exista la avioanle de pasageri si avioanele de lupta moderne. Nu numai ca este benefic pentru CA si FTC, este de asemenea folosit pentru diferite strategii de control optim adica utilizand actuatoare pentru a reduce rezistenta si cresterea eficientei.
Nu exista in literatura lucrari extinse despre CA care sa discute algoritmi, abordari si aplicatii. S-a demonstrat ca feed-backul sistemului de control cu actuatoare redundante poate fi redus la un sistem de control cu feed-back fara redundanta folosind un caz special al CA cunoscut ca 'inlantuirea Daisy'. In acest mod de abordare un subset al actionarii, considerat ca fiind actuatoarele principale, este folosit prima data apoi actuatoarele secundare sunt folosite numai daca cele primare ajung la saturatie.
CA apare cu metodele neliniare ca un feed-back. El se bazeaza pe separarea legii de control de sarcina alocarii controlului. Aceasta se face prin proiectarea unui controler pentru a oferi un 'control virtual' care v-a fi atasat la controlul semnalelor trimise catre actuator. Se ia in considerare un sistem supraactuat ca de exemplu un avion de pasageri sau un avion de lupta modern reprezentate de sistemul liniar urmator :
![]() (2.9)
(2.9)
unde ![]() poate fi :
poate fi :
![]()
ca urmare (2.9) devine:
![]()
unde ![]() este controlul virtual:
este controlul virtual:
![]()
Semnalul de
control ![]() este:
este:
![]()
unde
![]() este
pseudo-inversa a lui
este
pseudo-inversa a lui ![]() .
.
Matricea ![]() este care distribuie semnalele de control
pentru fiecare actuator disponibil. In cea mai mare parte a literaturii de specialitatea
greutatea
este care distribuie semnalele de control
pentru fiecare actuator disponibil. In cea mai mare parte a literaturii de specialitatea
greutatea ![]() .
In unele cazuri poate fi luata o alta optiune a matricei pondere
.
In unele cazuri poate fi luata o alta optiune a matricei pondere ![]() .
Intr-o problema de optimizare,
.
Intr-o problema de optimizare, ![]() poate fi aleasa pentru a obtine performantele
dorite luand in considerare constrangerile actuatorului.
poate fi aleasa pentru a obtine performantele
dorite luand in considerare constrangerile actuatorului.
Beneficiile CA sunt ca structura controlerului nu trebuie sa fie reconfigurata in cazul defectelor si poate fata defectului total al actuatorului: sistemul automat al CA redistribuie semnalele de control.
Ca si la MPC
un alt beneficiu major al CA este ca limitarile actuatorului pot fi manipulate,
inclusiv constrangerile actuatorului in procesul de optimizare. Unul din
neajunsurile CA este ca pentru sistemele neliniare factorizarea pura ![]() este o foarte puternica cerinta si prin urmare
trebuie facuta aproximarea
este o foarte puternica cerinta si prin urmare
trebuie facuta aproximarea ![]() .
In cazul controlului optimal al
suprafetelor de deviere, este necesara programarea liniara sau cuadrica. Acest
lucru este destul de dificil de realizat in timp real din cauza cerintelor de
inalta putere de calcul.
.
In cazul controlului optimal al
suprafetelor de deviere, este necesara programarea liniara sau cuadrica. Acest
lucru este destul de dificil de realizat in timp real din cauza cerintelor de
inalta putere de calcul.
Inversarea dinamica
O mare atractie a inversarii dinamice (DI) este capacitatea sa de a face modificari in conditiile de operare. Aceasta capacitate a motivat cercetatorii sa ia in considerare DI pentru controlul vehiculelor spatiale de reintrare in atmosfera. Acest vehicul are o gama larga de conditii de operare care variaza de la supersonic in timpul reintrarii la viteze subsonice.
Ideea de DI poate fi demonstrata daca se considera sistemul liniar :
![]()
Rearanjand
ecuatia cu privire la ![]() legea de control poate fi reprezentata :
legea de control poate fi reprezentata :
![]()
unde ![]() este o valoare de referinta predeterminata in
bucla inchisa. In DI este descris
ca un operator de tehnica de sinteza cu deficiente existente sau nedorite. Anularea si inlocuirea sunt
realizate prin selectia algebrica riguroasa a functiilor de feed-back. Din acest motiv metodologia feed-backului se
mai numeste liniarizare. Figura 2.11 arata un exemplu de ansamblu dinamic
neliniar invers cu interactiuni cu privire la reintrarea vehiculului. Principalele ipoteze in DI
sunt ca sistemul dinamic se presupune perfect modelat si prin urmare pot fi
anulate.
este o valoare de referinta predeterminata in
bucla inchisa. In DI este descris
ca un operator de tehnica de sinteza cu deficiente existente sau nedorite. Anularea si inlocuirea sunt
realizate prin selectia algebrica riguroasa a functiilor de feed-back. Din acest motiv metodologia feed-backului se
mai numeste liniarizare. Figura 2.11 arata un exemplu de ansamblu dinamic
neliniar invers cu interactiuni cu privire la reintrarea vehiculului. Principalele ipoteze in DI
sunt ca sistemul dinamic se presupune perfect modelat si prin urmare pot fi
anulate.
In practica aceasta ipoteza nu este realista. In relatiile cu aceasta
problema s-a sugerat utilizarea
metodelor de control robuste ca ![]() si
si ![]() pentru a minimiza sau suprima comportamentul
nedorit din cauza incertitudinilor sistemului care provoaca anulari dinamice
ale sistemului. Alte metode de
control cum ar fi retelele neuronale au
fost deasemenea propuse in literature de specialitate. Benecifiul DI este acela
ca nu necesita obtinerea de programare pentru a lucra intr-o gama larga de
conditii de functionare.
pentru a minimiza sau suprima comportamentul
nedorit din cauza incertitudinilor sistemului care provoaca anulari dinamice
ale sistemului. Alte metode de
control cum ar fi retelele neuronale au
fost deasemenea propuse in literature de specialitate. Benecifiul DI este acela
ca nu necesita obtinerea de programare pentru a lucra intr-o gama larga de
conditii de functionare.
DI are alocare de control si prin urmare are capacitatea de a redistribui semnalul de control in cazul defectelor.
Fig 2.11
In pofida acestor avantaje exista unele probleme in ceea ce priveste DI. In primul rand inversiunea dinamica neliniara (NDI) isi asuma integral feed-backul de stare. Aceasta nu este o problema la aeronavele moderne dar starea sistemului masurat nu este intotdeauna disponibila pentru multe alte sisteme. DI necesita o profunda intelegere si cunoastere a sistemelor pentru a fi in masura sa anuleze perfect dinamica sistemului.
In realitate acest lucru este imposibil. In present aceste limite de utilizare necesita un exterior robust. Inversiunea dinamica cu control adaptiv robust (ARC) se bazeaza pe activitatea in cazul in care o combinatie de SMC si control adaptive este conceputa si numita ARC. Controlerele au fost testate pentru mai multe tipuri de defecte cum ar fi pierderea eficientei zborului si defecte grave ale suprafetei. Schimbarea coeficientilor aerodinamici ai aeronavei din cauza defectelor si a defectiunilor structurii este estimata folosind identificarea online a parametrilor, pentru a obtine inversarea perfecta a sistemului neliniar.
2.4.6 Controlul robust
![]() este o
metodologie robusta de control si prin urmare poate fi considerat un sistem de
control al defectelor pasive.
este o
metodologie robusta de control si prin urmare poate fi considerat un sistem de
control al defectelor pasive. ![]() este una dintre cele mai dezvoltate metode de
control multivariabile cu multe aplicatii industriale. Cele mai robuste
abordari de control nu necesita nici o informatie cu privire la defecte si prin
urmare lucreaza atat in termeni nominali cat si in conditii de defecte.
Capacitatea de a face fata defectelor depinde de controlerul predefinit care se
bazeaza pe reducerea efectului de incertitudine sau perturbatii in sistem.
Primul pas in
este una dintre cele mai dezvoltate metode de
control multivariabile cu multe aplicatii industriale. Cele mai robuste
abordari de control nu necesita nici o informatie cu privire la defecte si prin
urmare lucreaza atat in termeni nominali cat si in conditii de defecte.
Capacitatea de a face fata defectelor depinde de controlerul predefinit care se
bazeaza pe reducerea efectului de incertitudine sau perturbatii in sistem.
Primul pas in ![]() este de a decide tipul si structura pentru a
putea fi luate in considerare. Aceste proces este oarecum dificil si necesita o
introducere in sistem. Cel mai general tip de incertitudine nestructurata este
bazat pe normalizarea factorului reprezentat.
este de a decide tipul si structura pentru a
putea fi luate in considerare. Aceste proces este oarecum dificil si necesita o
introducere in sistem. Cel mai general tip de incertitudine nestructurata este
bazat pe normalizarea factorului reprezentat.
Cea de-a
doua metoda este de alege frecventa dependenta de greutati pe baza unor
specificatii de performanta si apoi pentru a rezolva o problema de optimizare.
Un dezavantaj al ![]() este faptul ca in unele cazuri controlerul
este conservator in conditiile nominale pentru a garanta stabilitatea in caz de
defecte si performanta este uneori sacrificata.
este faptul ca in unele cazuri controlerul
este conservator in conditiile nominale pentru a garanta stabilitatea in caz de
defecte si performanta este uneori sacrificata.
Un alt dezavantaj este ca controlerul final foloseste un ordin mai mare decat sistemul. In unele cazuri este necesara reducerea modelului pentru a trunchea ordinul sistemului.
2.5Detectarea si izolarea defectelor
De fapt FTC si FDI joaca un rol esential pentru a oferi informatii cu privire la defectele din sistem si pentru a permite reconfigurarea adecvata. Prin urmare functia principala a FDI este sa detecteze eroarea/defectul si sa gaseasca locatia sa, astfel incat actiunea corectoare sa poate sa elimine sau sa minimizeze efectul asupra sistemului.
Se defineste:
-detectarea defectului: determinarea defectului prezent intr-un sistem si timpul de detectie
-izolarea defectului: determinarea felului defectului si timpul de detectare al acestuia.
-identificarea defectului: determinarea marimii defectului.
Pentru cele mai multe sisteme AFTC robustetea FDI are un efect puternic asupra robustetii FTC.
Un aspect important in FDI este redundanta. Cum s-a mentionat in 2.3 redundanta poate fi fie sub forma hardware fie redundanta analitica. De la aparitia tehnologiei fly by wire a existat o crestere a redundantei analitice. In redundanta analitica semnalele masurate sunt comparate cu un model matematic. Beneficiul folosirii redundantei analitice este clar: nu este nevoie de instalarea redundantei hardware, reducandu-se greutatea si costul.
2.5.1 Clasificarea FDI
Exista mai multe clasificari de FDI in literatura de specialitate. O clasificare evidenta este FDI bazat pe model si non-model. In aceasta teza accentul se v-a pune pe modelul bazat pe FDI. Avand in vedere strategia de toleranta a defectelor modelele bazate pe FDI sunt grupate pe baza capacitatilor lor in doua categorii:
-FDI care foloseste sisteme reziduale.
-FDI care au capacitatea de a estima defectele
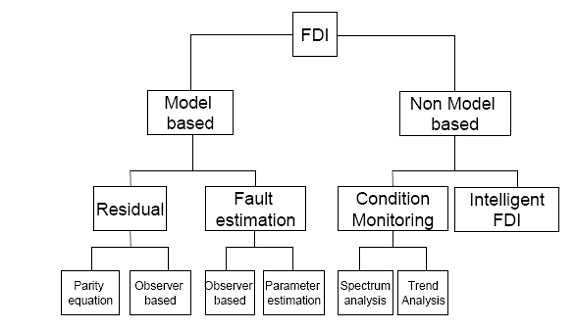
Fig 2.12
Conditia de monitorizare
Conditia de monitorizare este una dintre metodele traditionale folosite pe scara larga in industrie. Este important ca depistarea precoce a erorilor si defectelor in componente, cum ar fi posibilitatea de intretinere preventiva ce urmeaza a fi efectuata. Conditia de monitorizare este foarte populara in procesul de productie si in sistemele critice de non-siguranta. Conditia de monitorizare in cea mai mare parte depinde de masuratorile statistice luate de la anumite puncte de pe echipament si analize spectrale cum ar fi transformata Fourier rapida sau tendinta de analiza cum ar fi MTTF si MTBF.
Aceste instrumente de analiza furnizeaza informatii cu privire la starea de 'sanatate'. Analiza de la conditia de monitorizare permite planificarea avansata a intretinerii de rutina. Un dezavantaj al celor mai multe metode de monitorizare este procesul lent si obositor de colectare si interpretare a datelor. De asemenea, are o capacitate limitata de FTC si ca de obicei defectele pot fi detectate offline, deoarece se bazeaza pe datele colectate in timpul functionarii sistemului. O buna experienta sau o buna intretinere asigura date pentru analiza detectarii eroriilor sau defectelor. Conditia de monitorizare deasemenea sufera din cauza variatiei conditiilor de operare. Uneori, acest lucru inseamna ca este dificil sa se faca diferenta intre defecte sau exploatare defectoasa. Un alt dezavantaj in conditia de monitorizare este acela ca un singur defect poate cauza alarme multiple si uneori cauzeaza anomalii in datele colectate pentru alte unitati. Acest lucru face dificila localizarea sursei defectului.
FDI bazat pe semnale reziduale
In FDI bazate pe semnale reziduale, semnalele de la un model matematic si masuratorile hardware sunt comparate si filtrate iar diferenta formeaza un semnal rezidual. In conditia nominala fara defect, semnalele reziduale ar trebui sa fie zero si nonzero cand apar defecte. Acest semnal rezidual uneori se aplica cu un prag pentru a evita alarmele false de la perturbatii sau incertitudini. Cand semnalul rezidual depaseste pragul un defect este setat sa apara.
De obicei in generatia reziduala u defect este detectat si locatia sa este identificata, dar nu exista informatii suplimentare despre defecte.
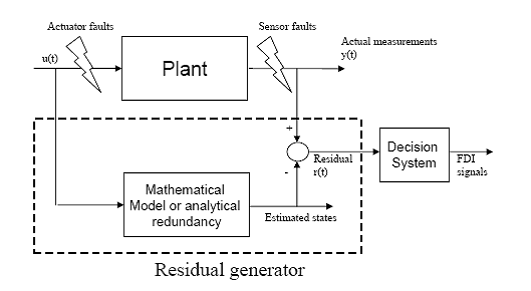
Fig 2.13
O buna cercetare asupra sistemelor FDI bazate pe semnale reziduale a fost facuta folosind diferite metode pentru diferite aplicatii. Exista multe beneficii in folosirea sistemelor FDI bazate pe semnale reziduale. Cele mai multe sisteme FDI bazate pe semnale reziduale sunt usor de inteles si usor de pus in aplicare. Pentru multe sisteme detectarea si izolarea erorilor/defectelor sunt suficiente pentru a declansa reconfigurarea FTC. De exemplu mai multe modele de controlere vor comuta la un anumit controler atunci cand defectul desemnat apare la acuatoare sau senzori. Cu toate acestea pentru anumite sisteme FTC detectarea si izolarea defectelor nu este suficienta. Unele sisteme FTC cer informatii suplimentare cu privire la natura ci comportamentul defectului.
Identificarea/estimarea defectului.Reconstructia FDI
Acest lucru este cu un pas mai avansat decat FDI bazat pe semnale reziduale dar este de cele mai multe ori specific pentru anumite controlere reconfigurabile. Anumite controlere FTC necesita o estimare a eficientei actuatorului pentru a permite controlerului FTC sa tolereze erorile/defectele. Din punct de vedere al senzorului, defectul FTC in cazul in care defectul senzorului poate fi estimat/reconstruit, aceste informatii pot fi folosite direct pentru a corecta masuratorile senzorului defect inainte ca acestea sa fie utilizate de operator. Aceasta metoda evita reconfigurarea controlerului pentru a fi tolerant cu erorile/defectele senzorului. Acest lucru v-a fi luat in considerare in ceea ce urmeaza.
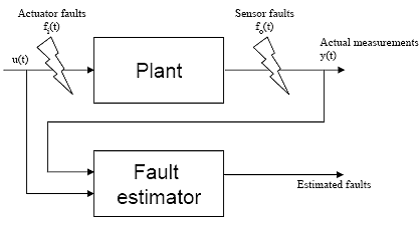
Fig 2.14
2.6 Comparatii ale diferitelor modele FDI
In acest capitol vor fi discutate unele dintre cele mai recente medode FDI de control al zborului.
2.6.1 Modelul de baza
Mai jos sunt discutii cu privire la unele metode de model de baza FDI cu aplicatii in litaratura de specialitate.
Filtrul Kalman
Aceasta este probabil una dintre cele mai cunoscute metode folosite in industrie. Un filtru Kalman pe scurt este un estimator optimal bazat pe observatii indirecte, inexacte si incerte. Este recursiv astfel incat masuratorile noi pot fi procesate pe masura ce sosesc. Daca toate zgomotele sunt Gaussiene, filtrul Kalman minimizeaza media patrata de eroare a parametrilor estimati si deci este optimala. Filtrul Kalman este folosit in industrie din mai multe motive :
-filtrul Kalman furnizeaza rezultate destul de exacte ca urmare a structurii sale optimale.
-filtrul Kalman are o forma recursiva si este potrivit pentru procesarea online in timp real si usor de pus in aplicare.
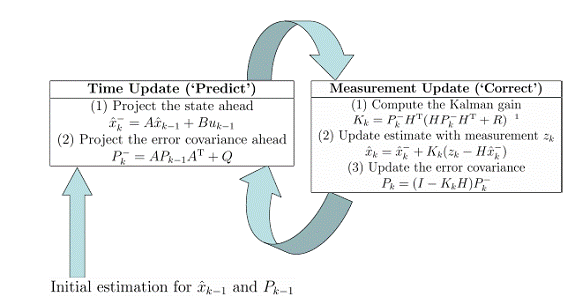 Figura
2.15
Figura
2.15
Ideea din
spatele filtrului Kalman este descrisa in figura 2.15 unde ![]() reprezinta un sistem liniar discret in timp de
forma :
reprezinta un sistem liniar discret in timp de
forma :
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
Unde variabilele
aleatoare ![]() si
si![]()
![]() reprezinta procesul de masurare al zgomotului. Ciclul filtrului Kalman incepe
cu estimarea initiala a lui
reprezinta procesul de masurare al zgomotului. Ciclul filtrului Kalman incepe
cu estimarea initiala a lui ![]() si a erorii
si a erorii ![]() . Timpul de update blocheaza stadiul actual al
proiectului si eroarea covarianta estimeaza in timp. Masuratorile blocului de
update calculeaza gainul
. Timpul de update blocheaza stadiul actual al
proiectului si eroarea covarianta estimeaza in timp. Masuratorile blocului de
update calculeaza gainul ![]() al filtrului Kalman folosind eroarea
covarianta proiectata
al filtrului Kalman folosind eroarea
covarianta proiectata ![]() .
Datorita largii utilizari in industrie si popularitatea acestuia in randul
cadrelor universitare, nu este o surpriza faptul ca filtrele Kalman sunt de
asemenea folosite la diagnosticarea defectelor. Filtrul Kalman de baza
functioneaza in calitate de observer si prin urmare poate fi folosit pentru a
detecta defectele sau semnalele reziduale prin crearea de semnale reziduale
prin compararea rezultatului estimat cu cel real. Conceptul de baza al
filtrului Kalman a fost actualizat pentru a permite multe aplicatii cum ar fi
filtrul Kalman extins pentru analiza sistemelor liniare si a sistemelor FDI
neliniare si pentru estimarea parametrilor care urmeaza sa fie estimati. De
multe ori acesta introduce biliniaritati care pot fi depasite prin utilizarea
filtrelor Kalman extinse. Filtrul Kalman poate fi deasemenea format dintr-un
ansamblu de filtre Kalman pentru a creea semnale reziduale folosite la
detectarea erorilor/defectelor. O alta varianta numita filtru Kalman in doua
etape are capacitatea nu numai de a
detecta si izola defectele, are de asemenea capacitatea de a estima nivelul de
eficacitate al actuatoarelor.
.
Datorita largii utilizari in industrie si popularitatea acestuia in randul
cadrelor universitare, nu este o surpriza faptul ca filtrele Kalman sunt de
asemenea folosite la diagnosticarea defectelor. Filtrul Kalman de baza
functioneaza in calitate de observer si prin urmare poate fi folosit pentru a
detecta defectele sau semnalele reziduale prin crearea de semnale reziduale
prin compararea rezultatului estimat cu cel real. Conceptul de baza al
filtrului Kalman a fost actualizat pentru a permite multe aplicatii cum ar fi
filtrul Kalman extins pentru analiza sistemelor liniare si a sistemelor FDI
neliniare si pentru estimarea parametrilor care urmeaza sa fie estimati. De
multe ori acesta introduce biliniaritati care pot fi depasite prin utilizarea
filtrelor Kalman extinse. Filtrul Kalman poate fi deasemenea format dintr-un
ansamblu de filtre Kalman pentru a creea semnale reziduale folosite la
detectarea erorilor/defectelor. O alta varianta numita filtru Kalman in doua
etape are capacitatea nu numai de a
detecta si izola defectele, are de asemenea capacitatea de a estima nivelul de
eficacitate al actuatoarelor.
Aceasta capacitate este un bonus pentru sistemele FTC care depind de nivelul de eficacitate al actuatorului pentru reconfigurare.
![]() bazat pe FDI
bazat pe FDI
Folosind
aceleasi principii ca si pentru proiectarea controlerelor ![]() un observer poate fi proiectat prin aplicarea
tehnicilor de filtrare
un observer poate fi proiectat prin aplicarea
tehnicilor de filtrare ![]() ca un sistem FDI bazat pe semnale reziduale.
Ideea este de a permite semnalului rezidul sa fie sensibil numai la defecte ci
si sa fie robust impotriva perturbatiilor, modeland eroarea si zgomotul. Acest
lucru poate fi realizat prin selectarea gainului obeserverului care reduce
norma lui
ca un sistem FDI bazat pe semnale reziduale.
Ideea este de a permite semnalului rezidul sa fie sensibil numai la defecte ci
si sa fie robust impotriva perturbatiilor, modeland eroarea si zgomotul. Acest
lucru poate fi realizat prin selectarea gainului obeserverului care reduce
norma lui ![]() intre incertitudine si semnalul rezidual.
Filtrele cu detectie a defectelor , utilizand tehnici de filtrare
intre incertitudine si semnalul rezidual.
Filtrele cu detectie a defectelor , utilizand tehnici de filtrare ![]() ca un sistem FDI bazat pe semnal rezidual este
unul dintre cele mai populare sisteme FDI.
ca un sistem FDI bazat pe semnal rezidual este
unul dintre cele mai populare sisteme FDI.
Estimarea parametrilor FDI
Estimarea parametrilor este sinonima cu controlere cum ar fi inversarea dinamica neliniara si alte cateva controlere bazate pe neliniaritate. Sistemele de estimare a parametrilor asigura un mijloc de actualizare a parametrilor online al sistemului in timp real pentru reconfigurarea controlerului. Estimarea parametrilor este una dintre multele metode care au fost aplicate in aeronautica. Avioanele contin multi coeficienti in special aerodinamici care se schimba in functie de conditiile de operare.
Acesti parametri sunt de obicei preestimati offline in tunelul aerodinamic si in testele de zbor inainte de a fi folositi in zbor. Cu toate acestea la aparitia unor defecte nu exista preestimari exacte si de aceea ecesti coeficienti aerodinamici trebuie sa fie obtinuti online.
In matoda 'doi pasi'(TSM) estimarea parametrilor de stare originali este descompusa in estimarea starii si intr-o estimare ulterioara a parametrului liniar. Principala problema este data de primul pas al TSM care este cunoscut ca reconstructia caii de zbor.
Estimarea parametrilor bazati pe filtrele Kalman este folosita la sistemul FDI. In cele mai multe metode de estimare a parametrilor, pentru a obtine estimari mai bune s-ar putea sa fie necesar sa se introduca semnale de perturbatie.
Din acest motiv cele mai multe metode de estimare a parametrilor lucreaza cel mai bine in prezenta vantului si a rafalelor de vant. Cu toate acestea in multe aplicatii practice este greu si nu se recomanda sa se aplice semnale perturbatoare aditionale in special atunci cand defectele sau distrugerile structurale apar in sistem.
Modele multiple si interactiuni intre modele multiple
bazate pe FDI
In mai multe modele bazate pe FDI, este creat un ansamblu de modele cu anticiparea defectelor. Iesirile din acest ansamblu pot fi comparate cu valoarea reala a iesirii sistemului pentru a crea semnale reziduale. Aici modelul cu cea mai mica eroare este modelul care reprezinta defectele curente din sistem. Prin urmare defectele pot fi detectate si izolate iar controlerul asociat care se ocupa cu defectul respectiv este activat. Dezavantajul modelului bazat pe FDI este faptul ca este destul de greu sa includa toate defectele posibile. Prin urmare o solutie este de a utiliza mai multe modele intercative. In modelele interactive multiple bazate pe control reconfigurabil (fig 2.8). Este necesar un sistem FDI care asigura estimarea greutatii modelului. Cercetatorii au propus utilizarea unui ansamblu de filtre Kalman pentru a calcula aceste greutati in termeni de probabilitate de defecte individuale.
Aceste metode folosesc combinatii convexe ale modelelor predefinite. Greutatea modelului in sine asigura detectia defectului si un anumit tip de identificare pentru defectele partiale. Aceasta metoda poate fi folosita pentru detectarea distrugerilor structurale. De asemenea acest sistem sufera de aceleasi dezavantaje ca si abordarea modelului multiplu.
Paritatea ecuatiei bazate pe FDI
Redundantele intr-un sistem pot fi folosite pentru verificarea paritatilor masuratorilor si ulterior pentru senzorii FDI prin folosirea unui sistem de vot. Aceasta metoda este putin diferita de un observer bazat pe FDI deoarece redundantele sunt comparate direct intre ele cat si intre sistemul actual cu scopul de a verifica inconcsecventele prin folosirea semnalelor reziduale.
Nu sunt necesare observere pentru paritatea bazate pe FDI. Consideram un sistem cu senzori redundanti unde ecuatiile de masurare pot fi reprezentate:
![]()
unde ![]() este vector de masurare.
este vector de masurare.
![]() este vector de stare.
este vector de stare.
![]() este vectorul de zgomot.
este vectorul de zgomot.
Daca exista
mai multi senzori decat variabile care urmeaza a fi masurate atunci ![]() si rangul lui
si rangul lui ![]() .
.
![]()
unde ![]() ,
,
![]() ,
,
![]() .
.
Cand
conditia este satisfacuta paritatea reziduala ![]() este :
este :
 (2.12)
(2.12)
In ecuatia
de mai sus vectorul de paritate contine doar informatii despre defecte si
incertitudini si este independent de ![]() .
In ceea ce priveste paritatea ecuatiei bazate pe FDI, asigura un design mai putin
flexibil in comparatie cu observerele bazate pe FDI.
.
In ceea ce priveste paritatea ecuatiei bazate pe FDI, asigura un design mai putin
flexibil in comparatie cu observerele bazate pe FDI.
2.6.2 Non modelul de baza
Sisteme FDI inteligente
Una dintre principalele probleme asociate cu designul modelului de baza este disponibilitatea si calitatea sa. Erori care rezulta in urma modelelor imperfecte si inexacte vor afecta performanta sistemului sde diagnosticare al defectelor. Utilizarea modelului robust bazat pe metode care de obicei rezulta intr-un design care este prea conservator si insensibil la greseli si prea complicat.
De la sfarsitul anilor '90, a existat o crestere a cercetarii asupra metodelor FDI in special asupra celor care utilizeaza inteligenta artificiala si metode de calcul usor cum ar fi retelele neuronale si logica Fuzzy. S-a propus o combinatie numerica si simbolica de cunostinte intr-un sistem cu cadru unic.
Ideea a fost inspirata de munca anterioara care folosea observere pentru semnale reziduale si logica fuzzy pentru procesul de luare a deciziilor. La baza conceptului sta ideea de a structura retelele neuronale intr-o logica fuzzy care permite generarea de semnale reziduale, evaluarea si diagnosticarea defectului. Modelele neuro- fuzzy se iau in considerare cu un adaos de prag adaptiv in sistemele de detectare a erorilor pentru a atinge un anumit nivel de robustete.
Unul dinte beneficiile folosirii abordarii inteligente, in special retelele neuronale pentru FDI este abilitatea sa dea modela orice functie neliniara. In termenul FDI retelele neuronale au caracteristica de 'cutie neagra ' si prin urmare capacitate de a invata din 'exemple', care necesita informatii putine si putine cunostinte despre structuta sistemului. Sunt prezentate doua dezavantaje majore ale retelelor neuronale conventionale: de la o cunoastere Euristica de la experienta expertilor nu poate fi usor incorporata si caracteristica 'cutiei negre' inseamna ca, comportamentul sau intern nu poate fi usor inteles. Un alt dezavantaj al retelelor neuronale este lipsa intelegerii comportamentului sau intern cauzand probleme sistemului avionului.
2.6.3 Noi metode FDI
In ultimii ani unele metode noi si neconventionale de detectare a defectelor au aparut in literatura de specialitate. Exemple de astfel de metode sunt LPV bazate pe FDI si generarea semnalelor reziduale folosind metode de inalta fidelitate.
LPV bazat pe FDI sunt motivate de problema confruntarii cu o gama larga de conditii de functionare. Ca si proiectarea controlerelor FTC, FDI se bazeaza pe variatia parametrilor liniari. Chiar daca exista diverse abordai pentru FDI, LTI si LTV si sisteme biliniare sunt doar cateva metode disponibile pentru sitemul LPV. Prin urmare s-a pus accentul pe introducerea sistemului FDI de baza pentru sistemul LPV utilizand o extensie a abordarii numita 'problema fundamentala a generarii semnalului rezidual'.
Sistemele FDI bazate pe LPV au performante inerente si garantii pentru stabilitatea globala a conditiilor de operare, in comparatie cu alte metode.
Chiar daca se pare ca LPV bazat pe FDI are potential ridicat in special penru sistemele de avioniva, inca exista cercetare in acest domeniu. Unele sisteme sunt bine cunoscute iar modele aproape non liniare si de inalta fidelitate pot fi obtinute. Sisteme ca avioanele sunt bine intelese si reprezinta unul dintre cele mai studiate siteme cu toti coeficientii aerodinamici obtinuti prin ample cercetari in laborator cu tunele aerodinamice si teste de zbor.
Un defect poate fi declarat atunci cand semnalul rezidual depaseste pragul predeterminat.
2.7 Concluzii
Acest capitol a prezentat o scurta introducere in domeniul FTC si FDI. Acestea include definitii pentru termenii utilizati in mod regulat in FTC si FDI cum sunt defectele si erorile. In acest capitol au fost de asemenea discutate pe scurt tipurile de defecte si erori la actuatoare si senzori. Au fost discutate diferite metode ale FTC bazate pe modul in care toleranta la defecte este obtinuta variind de la control robust la redistribuirea semnalului de control.
Capitolul 3
Controlul Modului de Alunecare
Acesta a fost conceput in URSS in anii '50 si s-a raspandit in Vest in anii '70. SMC este un tip de control non-liniar si un caz special de control al structurii variabile. Este o metodologie de control robust. Designul controlerului este unic comparativ cu alte metode de control deoarece performantele controlerului depind de designul supafetei de alunecare si nu de urmarirea directa a starii. Ideea este de a forta traiectoria starii spre suprafata de alunecare si odata atinsa, starile sunt fortate sa ramana pe suprafata respectiva. Controlul modului de alunecare are o proprietate robusta la un anumit tip de incertitudine, care face SMC un candidat puternic pentru FTC pasive cand actuatorul se defecteaza. SMC are potentialul de a deveni o alternativa la controlul reconfigurabil, si are capacitatea de a mentine performantele necesare fara a necesita un FDI. In capitolul anterior tabelul 2.1 indica faptul ca SMC este definit ca o metodologie de control robusta si are capacitatea de a manipula daunele structurale si defectele actuatorului fara reconfigurare. Obiectivul acestui capitol este de a introduce conceptul de moduri de alunecare si de a examina proprietatile sale, in scopul de a sublinia beneficiile sale in domeniile FTC si FDI. Pentru a introduce conceptul de SMC este intreprinsa o analiza pe baza unui simplu pendul.
3.1 Introducere
Exista doua etape pentru proiectarea controlerelor SMC. In primul rand sunt proiectate suprafetele de alunecare. Numai atunci pot fi proiectate legile de control, astfel incat alunecarea este realizata si se mentine pe suprafata. Odata ce apare alunecarea, robustetea la un anumit tip de incertitudine este garantata si sistemul se comporta ca o miscare redusa independenta de control. Performanta controlerului depinde de alegerea suprafetei de alunecare. Un exemplu tipic de mod de alunecrae este legea de control formata din componente liniare si neliniare. Legea de control neliniara conduce starile spre suprafata de alunecare si odata ajunse la suprafata legea de control liniara devine din ce in ce mai mult dominanta fata de cea neliniara. Partea neliniara determina proprietatile de robustete ale controlerului.
3.1.1 Forma regulata
In scopul explicarii modului de alunecare si proprietatile sale, in mod convenabil sistemul trebuie sa fie transformat intr-o forma canonica adecvata. Se ia in considerare urmatorul sistem liniar invariant in timp(LTI):
![]() (3.1)
(3.1)
unde ![]() ,
,
![]()
![]() ,
,![]() .
.
Presupunem
ca ![]() si
si ![]() este controlabila. Deoarece
este controlabila. Deoarece ![]()
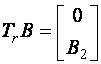 (3.2)
(3.2)
unde ![]() nesingulara.
nesingulara.
Matricea
ortogonala ![]() poate fi calculata folosind descompunerea
"QR".
poate fi calculata folosind descompunerea
"QR".
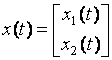 (3.3)
(3.3)
Unde ![]() ;
;![]() astfel incat ecuatia(3.1) se scrie ca:
astfel incat ecuatia(3.1) se scrie ca:
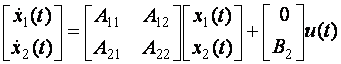 (3.4)
(3.4)
Aceasta reprezinta forma regulata.
Definim o combinatie liniara a starilor ca:
![]() (3.5)
(3.5)
unde ![]() iar
iar
![]() se poate scrie ca:
se poate scrie ca:
![]() (3.6)
(3.6)
Ecuatia
(3.5) se numeste functia de comutatie. Matricea ![]() se poate scrie ca:
se poate scrie ca:
![]() (3.7)
(3.7)
unde ![]() .
.
![]() se alege astfel incat
se alege astfel incat![]() In timpul alunecarii
In timpul alunecarii ![]() pentru
pentru ![]()
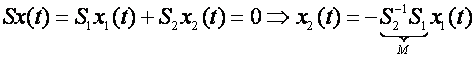 (3.8)
(3.8)
Ecuatia
(3.8) implica faptul ca odata ce ![]() este cunoscut starile
este cunoscut starile ![]() sunt complet determinate. De aceea din ecuatia
(3.4) se ia in considerare numai
sunt complet determinate. De aceea din ecuatia
(3.4) se ia in considerare numai ![]()
![]() (3.9)
(3.9)
Si apoi
substituim ![]() din (3.8) in (3.9) rezulta
din (3.8) in (3.9) rezulta
![]() (3.10)
(3.10)
unde ![]() . Alegerea suprafetei
. Alegerea suprafetei ![]() in (3.6) in mod clar afecteaza dinamica in
(3.10) prin proiectarea lui
in (3.6) in mod clar afecteaza dinamica in
(3.10) prin proiectarea lui ![]() in (3.8). stabilitatea sistemului in (3.10)
depinde de ordinea redusa a perechii
in (3.8). stabilitatea sistemului in (3.10)
depinde de ordinea redusa a perechii ![]() Astfel proiectarea lui
Astfel proiectarea lui ![]() depinde
de controlabilitatea perechii
depinde
de controlabilitatea perechii ![]() .
Perechea de matrici
.
Perechea de matrici ![]() este controlabila daca
este controlabila daca ![]() este controlabila. Cu alte cuvinte daca sistemul
original este controlabil
este controlabila. Cu alte cuvinte daca sistemul
original este controlabil ![]() poate
fi proiectat folosind metoda de stare cu feed-back clasica si odata ce a fost
obtinut si suprafata
poate
fi proiectat folosind metoda de stare cu feed-back clasica si odata ce a fost
obtinut si suprafata ![]() poate fi obtinuta. In ansamblu problema
proiectarii controlului modului de alunecare poate fi vazuta ca :
poate fi obtinuta. In ansamblu problema
proiectarii controlului modului de alunecare poate fi vazuta ca :
proiectarea
matricei ![]() pentru a atinge nivelul de performanta necesar
si o stabilitate pentru bucla in circuit inhis a modului de alunecare.
pentru a atinge nivelul de performanta necesar
si o stabilitate pentru bucla in circuit inhis a modului de alunecare.
Proiectarea unei legi de control pentru a se asigura ca suprafata de alunecare este atinsa si ulterior mentinuta.
Aceasta
procedura de proiectare este unica si diferentiaza SMC de alte metode clasice.
Orice metoda de stare cu feed-back poate fi folosita pentru a calcula pe ![]() iar apoi
matricea
iar apoi
matricea ![]() poate fi scrisa ca:
poate fi scrisa ca:
![]() (3.11)
(3.11)
Matricea
nesingulara ![]() poate fi arbitrar aleasa, dar pentru usurarea
calculelor adesea se alege
poate fi arbitrar aleasa, dar pentru usurarea
calculelor adesea se alege ![]() .
.
Urmatoarele
abordari clasice pot fi alese pentru a obtine matricea ![]() iar
apoi pe
iar
apoi pe ![]() .
.
1. minimizarea cuadrica.
2. rezistenta robustetii.
3. atribuirea rezistentii directe.
Abordarile recente
pentru proiectarea lui ![]() se bazeaza pe inegalitatea matricilor liniare
(LMI). Legea de control
se bazeaza pe inegalitatea matricilor liniare
(LMI). Legea de control ![]() nu este proiectata pentru a specifica direct
dinamica dorita pentru sistemul in bucla inchisa, dar mai degraba pentru a
asigura ca suparfata de control este atinsa si miscarea
nu este proiectata pentru a specifica direct
dinamica dorita pentru sistemul in bucla inchisa, dar mai degraba pentru a
asigura ca suparfata de control este atinsa si miscarea ![]() este obtinuta. In literatura
este obtinuta. In literatura ![]() este proiectat pentru ca conditiile de
saturare sa fie indeplinite. In cazul unei singure intrari in sistem:
este proiectat pentru ca conditiile de
saturare sa fie indeplinite. In cazul unei singure intrari in sistem:
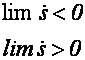 (3.12)
(3.12)
sau mai compact
![]() (3.13)
(3.13)
unde ![]() .
Aceasta este adesea numita conditia de atingere. O conditie mai stricta de
'atingere' pentru a se asigura ca legea de control
.
Aceasta este adesea numita conditia de atingere. O conditie mai stricta de
'atingere' pentru a se asigura ca legea de control ![]() este conceputa astfel incat suprafata de
alunecare este atinsa in ciuda prezentei incertitudinilor, si in timp finit
este data de:
este conceputa astfel incat suprafata de
alunecare este atinsa in ciuda prezentei incertitudinilor, si in timp finit
este data de:
![]() (3.14)
(3.14)
Unde ![]() este un scalar pozitiv.
este un scalar pozitiv.
Observatii
- ![]() nu are nici un efect direct asupra dinamicii
modului de alunecare. In ecuatiile (3.8) si (3.11)
nu are nici un efect direct asupra dinamicii
modului de alunecare. In ecuatiile (3.8) si (3.11) ![]() actioneaza doar ca un factor de scalare pentru
schimbarea functiei.
actioneaza doar ca un factor de scalare pentru
schimbarea functiei.
- in analiza de mai sus in timpul unui mod de alunecare ideal sistemul in bucla inchisa care reglementeaza miscarea de alunecare data de ecuatia (3.10) este de ordin redus.
- pentru sisteme multivariabile ecuatia (3.14) este de forma:
![]() (3.15)
(3.15)
Unde ![]() este un scalar pozitiv
este un scalar pozitiv
3.1.2 Proprietati ale modului de alunecare
In timpul alunecarii :
- Sistemul se comporta ca o miscare redusa care
nu depinde de ![]()
- Exista ![]() stari care determina dinamica sistemului in
bucla inchisa
stari care determina dinamica sistemului in
bucla inchisa
- Miscarea de alunecare in bucla inchisa depinde numai de suprafata de alunecare
- Polii miscarii de alunecare sunt dati de
zerourile invariante ale sistemului ![]() .
.
O a cincea proprietate care este cea mai importanta in termeni FTC pentru manipularea defectelor actuatorului este discutata in continuare. Se considera sistemul liniar:
![]() (3.16)
(3.16)
unde ![]() este cunoscuta si reprezinta incertitudinea. In timpul
alunecarii:
este cunoscuta si reprezinta incertitudinea. In timpul
alunecarii:
![]() (3.17)
(3.17)
care implica
![]() (3.18)
(3.18)
Rearanjand
ecuatia in functie de ![]() rezulta
rezulta
![]() (3.19)
(3.19)
Cantitatea![]() se numeste control echivalent si este valoarea medie teoretica pentru care
semnalul de control trebuie sa o aiba pentru a mentine miscarea de alunecare pe
S. Substituind
se numeste control echivalent si este valoarea medie teoretica pentru care
semnalul de control trebuie sa o aiba pentru a mentine miscarea de alunecare pe
S. Substituind ![]() in (3.16) rezulta
in (3.16) rezulta
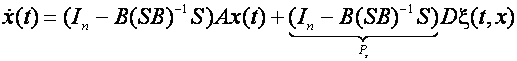
Este usor de
verificat ca ![]() satisface conditia:
satisface conditia:
![]() (3.21)
(3.21)
Daca ![]() atunci D=BR,
atunci D=BR, ![]()
![]() (3.22)
(3.22)
Si deoarece![]() rezulta
rezulta
![]() (3.23)
(3.23)
Se poate
vedea ca in timpul unei miscari de alunecare ideala incertitudinea ![]() nu afecteaza miscarea de alunecare.
nu afecteaza miscarea de alunecare.
3.2 Pendulul
In aceasta sectiune se vor aplica metodele de mai sus la un pendul pentru a oferi o introspectiva in proiectarea sistemului SMC si a miscarii de alunecare. Se considera un pendul tipic care consta dintr-o greutate si un fir care este actionat de un motor de cuplu la punctul de suspensie. Obiectivul este de a proiecta un controler de mod de alunecare astfel incat pendulul sa ramana la verticala, cand acesta este lasat sa se balanseze. Dinamicile buclei inchise sunt alese pentru a fi solutionate in mai putin de 3 secunde fara a depasi unghiul de deplasare al pendulului. Se considera urmatorul sistem. Ecuatia dinamica este data de
![]() (3.24)
(3.24)
Unde ![]() reprezinta deplasarea unghiulara facuta de
verticala,
reprezinta deplasarea unghiulara facuta de
verticala, ![]() este cuplul aplicat,
este cuplul aplicat, ![]() este masa,
este masa, ![]() este acceleratia gravitationala,
este acceleratia gravitationala, ![]() este lungimea firului.
este lungimea firului.
Figura 3.1
Exemplu
Presupunem ![]() ,
,
![]() ,
,
![]() .
Liniarizand ecuatia (3.24) in jurul verticalei pozitiei de echilibru
randamentul este:
.
Liniarizand ecuatia (3.24) in jurul verticalei pozitiei de echilibru
randamentul este:
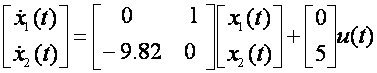 (3.25)
(3.25)
unde starile ![]() reprezinta
reprezinta ![]() care sunt deplasarile unghiulare si viteza
unghiulara. Matricea
care sunt deplasarile unghiulare si viteza
unghiulara. Matricea ![]() are un singur non-zero in partea de jos si
este o forma regulate ca in (3.4). Primul pas este proiectarea suprafetei de
alunecare adica matricea
are un singur non-zero in partea de jos si
este o forma regulate ca in (3.4). Primul pas este proiectarea suprafetei de
alunecare adica matricea ![]() .
In timpul unei miscari ideale de alunecare
.
In timpul unei miscari ideale de alunecare ![]() .
Din (3.8) rezulta:
.
Din (3.8) rezulta:
![]() (3.26)
(3.26)
unde ![]() si
si ![]() sunt scalari. Substituind (3.26) in (3.25)
rezulta
sunt scalari. Substituind (3.26) in (3.25)
rezulta
![]() (3.27)
(3.27)
si solutia este ![]()
![]() reprezinta timpul in care are loc alunecarea.
Daca
reprezinta timpul in care are loc alunecarea.
Daca ![]() rezulta
rezulta
![]() (3.28)
(3.28)
Se considera urmatoarea lege de control
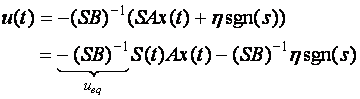 (3.29)
(3.29)
Unde ![]() este un scalar pozitiv
este un scalar pozitiv
![]() (3.30)
(3.30)
Inlocuid (3.29) in (3.30) rezulta
![]() (3.31)
(3.31)
![]() (3.32)
(3.32)
Prin urmare
legea de control aleasa ![]() satisface conditia de atingere
satisface conditia de atingere ![]() in (3.15). Folosind matricea
in (3.15). Folosind matricea ![]() obtinuta prin proiectarea lui (3.28) si
obtinuta prin proiectarea lui (3.28) si ![]() rezulta
rezulta
![]() (3.33)
(3.33)
3.2.1 Simulari si rezultate
3.2.2 O lege de control practica
Se considera urmatoarea lege de control
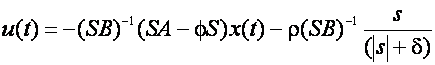 (3.35)
(3.35)
Unde ![]() este un scalar negativ. Cantitatea
este un scalar negativ. Cantitatea ![]() este un scalar mic pozitiv si
este un scalar mic pozitiv si ![]() depinde de magnitudinea incertitudinii.
Diferenta intre controlerul din ecuatia (3.35) si (3.29) este introducerea
termenului
depinde de magnitudinea incertitudinii.
Diferenta intre controlerul din ecuatia (3.35) si (3.29) este introducerea
termenului ![]() si aproximarea termenului sgn(s). Alegem
si aproximarea termenului sgn(s). Alegem ![]() ,
,
![]() ,
,
![]() .
Ecuatia (3.35) devine
.
Ecuatia (3.35) devine
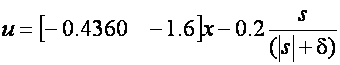
3.3 Vectorul unitate
In sectiunea anterioara a fost introdusa o practica de proiectare pentru un controler pentru un sistem pendular. Sistemul pendular reprezinta un sistem cu o singura intrare. Cea mai convenabila structura de control pentru sisteme multivariabile ditr-o perspectiva a modului de alunecare este vectorul unitate. Aceasta metoda va forma baza proiectarii controlerului in aceasta teza. Se considera un sistem cu o incertitudune matematica
![]() (3.36)
(3.36)
unde ![]() .
.
![]() (3.37)
(3.37)
Exista o transformare ortogonala astfel incat sistemul de mai sus sa fie transformat in urmatoarea forma regulata
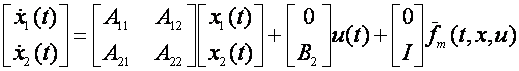 (3.38)
(3.38)
unde ![]() este o proiectia a lui
este o proiectia a lui ![]() in forma coordonatelor regulate. De aici
in forma coordonatelor regulate. De aici
![]() (3.39)
(3.39)
Deci forma
Euclidiana a lui ![]() este pastrata de catre transformarea
ortogonala. In
forma sa regulata functia de comutare
este pastrata de catre transformarea
ortogonala. In
forma sa regulata functia de comutare ![]() poate fi scrisa ca
poate fi scrisa ca
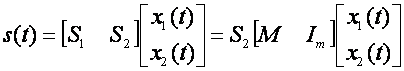 (3.40)
(3.40)
Alegerea lui
![]()
![]() este arbitrara dar aici este aleasa astfel
incat
este arbitrara dar aici este aleasa astfel
incat
![]() (3.41)
(3.41)
unde ![]()
![]() este matrice diagonala nesingulara. Definim o
alta transformare de coordonate astfel incat sistemul sa poata fi impartit in:
este matrice diagonala nesingulara. Definim o
alta transformare de coordonate astfel incat sistemul sa poata fi impartit in:
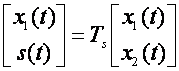 (3.42)
(3.42)
unde
matricea de transformare ![]() este data de
este data de
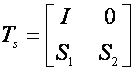 (3.43)
(3.43)
Apoi sistemul(3.38) poate fi scris ca
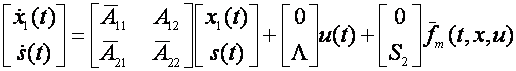 (3.44)
(3.44)
unde
![]()
Legea de control a lui Ryan si Corless cuprinde componente liniare si neliniare date de
![]() (3.45)
(3.45)
Componenta liniara este
![]() (3.46)
(3.46)
unde ![]() si componenta neliniara este
si componenta neliniara este
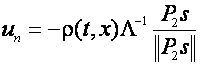 (3.47)
(3.47)
unde ![]() este o matrice simetrica pozitiva care
satisface ecuatia Lyapunov.
este o matrice simetrica pozitiva care
satisface ecuatia Lyapunov.
![]() (3.48)
(3.48)
Functia
scala ![]() depinde de marimea incertitudinii si este orice functie care satisface conditia
depinde de marimea incertitudinii si este orice functie care satisface conditia
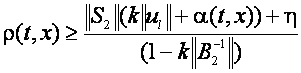 (3.49)
(3.49)
unde ![]() ,
,
![]() =const,
=const,
![]()
Analiza stabilitatii pentru un sistem in bucla inchisa
Problema determinarii stabilitatii unui sistem in bucla inchisa sub influenta unor incertitudini potrivite devine o problema a asigurarii alunecarii in ciuda prezentei incertitudinii. Acest lucru se datoreaza faptului ca atunci cand controlerul induce o miscare de alunecare ideala sistemului in bucla inchisa este stabil din proiectare. Aceasta sectiune v-a arata ca controlerul vectorului unitate (3.45) tot v-a induce alunecarea in pofida prezentei incertitudinii. Substituind legea de control (3.45) in (3.44) rezulta
![]() (3.50)
(3.50)
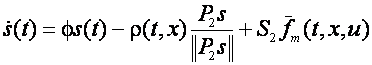 (3.51)
(3.51)
Se considera functia Lyapunov ![]() . Diferentiind functia
Lyapunov rezulta
. Diferentiind functia
Lyapunov rezulta
![]() (3.52)
(3.52)
Deoarece ![]() .
.
Deoarece ![]() rezulta
rezulta
![]() (3.53)
(3.53)
Ideea este sa reprezentam pe ![]() in (3.53) in functie de gradul de
incertitudine
in (3.53) in functie de gradul de
incertitudine ![]() , folosind pe
, folosind pe ![]() in (3.49). Din (3.45) si (3.47) folosind
proprietatea de inegalitate a triunghiului rezulta
in (3.49). Din (3.45) si (3.47) folosind
proprietatea de inegalitate a triunghiului rezulta
![]() (3.54)
(3.54)
Ecuatia (3.49) poate fi scrisa ca:
![]() (3.55)
(3.55)
Rearanjand ecuatia rezulta
![]() (3.56)
(3.56)
Din ecuatia (3.54) si (3.37) ecuatia de mai sus poate fi scrisa ca
![]() (3.57)
(3.57)
Inlocuind (3.57) in (3.53) rezulta
![]() (3.58)
(3.58)
3.3.2 Unitatea vector, termenul de pseudo-alunecare
In obtinerea acestei miscari de alunecare ideale apare frecventa discontinua, infinita de schimbare sau chattering. Aceasta este inoportuna pentru unele sisteme practice, in special in cazul sistemelor mecanice cu actuatoare predispuse la uzura. Prin urmare este necesar ca aceasta discontinuitate sa fie aplatizata si se obtine o aproximare a alunecarii ideale. Aici starile sistemului sunt necesare doar pentru a ramane aproape de suprafata de alunecare si nu pe suprafata. Totusi proprietatile de robustete ale incertitidinii potrivite nu mai sunt garantate. Pe de alta parte in cazul in care aproximarea este destul de aproape de valoarea reala a discontinuitatii o buna aproximare a alunecarii ideale inca poate fi obtinuta. De aceea este un compromis intre robustete si reducerea efectului de chattering. Exista mai multe metode folosite pentru a obtine pseudo-alunecarea; dar cea care este folosita in aceasta teza se bazeaza pe metoda numita 'aproximare fractionara'. Alte metode de aproximare sunt abordarea stratului limita si puterea legii de interpolare. Termenul neliniar al legii de control din ecuatia (3.35) este dat de:
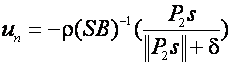 (3.60)
(3.60)
unde ![]() .
Daca
.
Daca ![]() aproximarea v-a fi mai buna cu functia
discontinua sgn(s); dar pentru a reduce chatteringul
aproximarea v-a fi mai buna cu functia
discontinua sgn(s); dar pentru a reduce chatteringul ![]() trebuie sa fie mai mare.
trebuie sa fie mai mare.
3.4 Proiectarea suprafetei de alunecare
In acest
subcapitol se v-a discuta proiectarea suprafetei de schimbare in special a
matricei ![]() si a functiei de comutatie
si a functiei de comutatie ![]() .
.
3.4.1 Minimizarea cuadrica
Se considera sistemul liniar
![]() (3.61)
(3.61)
Cu semnalul de eroare
![]() (3.62)
(3.62)
Problema
regulatorului liniar cuadric (LQR) este de a gasi intrarea de control ![]() pentru a minimiza costul energiei.
pentru a minimiza costul energiei.
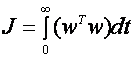 (3.63)
(3.63)
Cu alte
cuvinte gasirea efortului optim pentru a obtine performantele dorite.
Presupunem ca ![]() este inversabila si egala cu zero. Ecuatia
(3.62) se substituie in (3.63)
este inversabila si egala cu zero. Ecuatia
(3.62) se substituie in (3.63)
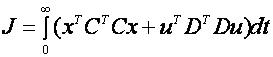 (3.64)
(3.64)
Daca ![]() si
si ![]() atunci rezulta
atunci rezulta
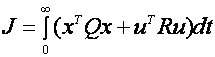 (3.65)
(3.65)
u(t)=Kx(t) unde
![]() (3.66)
(3.66)
Si ![]() satisface conditia
satisface conditia
![]() (3.67)
(3.67)
In proiectarea suprafetei de alunecare controlul intrarii nu este considerat in mod explicit.
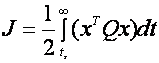 (3.68)
(3.68)
unde ![]() este timpul de inceput al alunecarii. Se
considera transformarea de coordonata
este timpul de inceput al alunecarii. Se
considera transformarea de coordonata ![]() . Matricea Q in forma regulata poate fi scrisa
ca
. Matricea Q in forma regulata poate fi scrisa
ca
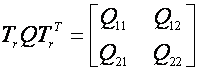 (3.69)
(3.69)
unde ![]() .
De aici in forma regulata LQR poate fi scris ca
.
De aici in forma regulata LQR poate fi scris ca
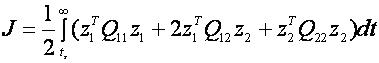 (3.70)
(3.70)
Ecuatia (3.70) nu are forma starii de feed-back a LQR.
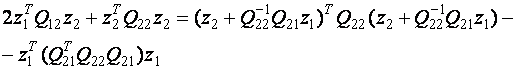 (3.71)
(3.71)
Folosind (3.71) ecuatia (3.70) poate fi scrisa ca
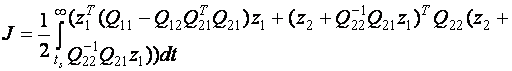
Definim
![]() (3.73)
(3.73)
Si pseudo controlul este
![]() (3.74)
(3.74)
Ecuatia (3.72) poate fi scrisa ca
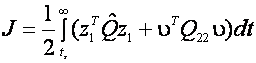 (3.75)
(3.75)
Minimizarea este asociata cu sistemul dinamic in ecuatia (3.9) care este dat de formula
![]() (3.76)
(3.76)
Eliminand pe ![]() in (3.76) folosind (3.74) sistemul devine
in (3.76) folosind (3.74) sistemul devine
![]() (3.77)
(3.77)
Legea de control optimal este
![]() (3.78)
(3.78)
Unde ![]() satisface conditia
satisface conditia
![]() (3.79)
(3.79)
Daca s(t)=0 atunci
![]() (3.80)
(3.80)
Din (3.74) si (3.78) rezulta
![]() (3.81)
(3.81)
Si deci matricea M se defineste ca
![]() (3.82)
(3.82)
Odata ce ![]() a fost obtinuta matricea
a fost obtinuta matricea ![]() poate fi calculata folosind (3.11) unde
poate fi calculata folosind (3.11) unde ![]() poate
fi aleasa in mod arbitrar. In aceasta teza
poate
fi aleasa in mod arbitrar. In aceasta teza ![]() v-a fi
ales astfel incat
v-a fi
ales astfel incat ![]()
Proiectarea controlerului pentru urmarire
Legea de control a fost proiectata astfel incat traiectoria sistemului sa revina la punctul de echilibru.
In [67] sunt discutate in detaliu doua metode : urmarirea folosind actiunea integrala si abordarea modelului de referinta.
3.5.1 Abordarea actiunii integrale
Se considera sistemul liniar regulat
![]() (3.83)
(3.83)
Unde ![]()
![]() (3.84)
(3.84)
Unde ![]()
![]() (3.85)
(3.85)
Unde ![]() este semnalul de referinta filtrat
este semnalul de referinta filtrat
![]() (3.86)
(3.86)
unde ![]() si este o matrice stabila, iar
si este o matrice stabila, iar ![]() este un vector constant. Semnalul
este un vector constant. Semnalul ![]() reprezinta pasul schimbarii in cerinta care nu
este diferentiabil la un anumit interval de timp. Ecuatia (3.86) reprezinta o
versiune a semnalului
reprezinta pasul schimbarii in cerinta care nu
este diferentiabil la un anumit interval de timp. Ecuatia (3.86) reprezinta o
versiune a semnalului ![]() si deci aceasta ecuatie poate fi vizualizata
in termeni clasici ca o prefiltrare a semnalului. Analiza sistemului de
urmarire este descrisa mai jos
si deci aceasta ecuatie poate fi vizualizata
in termeni clasici ca o prefiltrare a semnalului. Analiza sistemului de
urmarire este descrisa mai jos
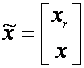 (3.87)
(3.87)
Sistemul augumentat poate fi scris sub forma
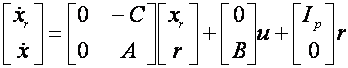 (3.88)
(3.88)
Deoarece perechea ![]() se presupune ca este in forma regulata starea
se presupune ca este in forma regulata starea ![]()
![]() poate fi impartita ca in
poate fi impartita ca in
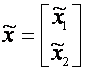 (3.89)
(3.89)
Putem scrie noua forma
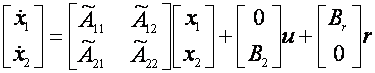 (3.90)
(3.90)
unde matricea sistemului augumentat si impartit este
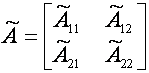 (3.91)
(3.91)
si
 (3.92)
(3.92)
In expresia
(3.91) matricea ![]() este o partitie a matricei C. obiectivul este
sa proiectam o suprafata de alunecare de forma
este o partitie a matricei C. obiectivul este
sa proiectam o suprafata de alunecare de forma
![]() (3.93)
(3.93)
unde ![]() este proiectata sa indeplineasca performantele
specificate pentru sistemul de ordin redus in bucla inchisa. Matricea
este proiectata sa indeplineasca performantele
specificate pentru sistemul de ordin redus in bucla inchisa. Matricea ![]() poate fi impartita ca mai jos:
poate fi impartita ca mai jos:
![]() (3.94)
(3.94)
Presupunem
ca ![]() este o matrice diagonala nesingulara. In
timpul unei miscari de alunecare ideala sistemul de ordin redus este
reglementat de partitia de sus ecuatiei
(3.90) care este:
este o matrice diagonala nesingulara. In
timpul unei miscari de alunecare ideala sistemul de ordin redus este
reglementat de partitia de sus ecuatiei
(3.90) care este:
![]() (3.95)
(3.95)
In timpul miscarii de alunecare s(t)=0 si deci
![]() (3.96)
(3.96)
si
![]() (3.97)
(3.97)
unde  .
Substituind (3.97) in partea de sus a lui (3.90) rezulta
.
Substituind (3.97) in partea de sus a lui (3.90) rezulta
![]() (3.98)
(3.98)
Proiectarea
unui hiperplan este determinat de controlabilitatea perechii ![]() .
Daca sistemul triplu
.
Daca sistemul triplu ![]() este complet controlabil si nu are nici un
zero invariant in origine atunci perechea
este complet controlabil si nu are nici un
zero invariant in origine atunci perechea ![]() este perfect controlabila. Daca conditia de
mai sus este satisfacuta atunci metoda de proiectare descris in (3.41) poate fi
folosita pentru sistemul de mai sus. Metoda vectorului unitate descrisa
anterior va fi aplicata sistemului augumentat de mai sus. Mai intai transformam
sistemul folosind schimbarea de coordonate asociate cu matricea:
este perfect controlabila. Daca conditia de
mai sus este satisfacuta atunci metoda de proiectare descris in (3.41) poate fi
folosita pentru sistemul de mai sus. Metoda vectorului unitate descrisa
anterior va fi aplicata sistemului augumentat de mai sus. Mai intai transformam
sistemul folosind schimbarea de coordonate asociate cu matricea:
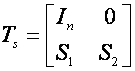 (3.99)
(3.99)
rezulta
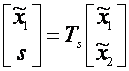 (3.100)
(3.100)
si sistemul poate fi scris ca
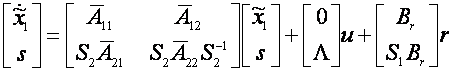 (3.101)
(3.101)
unde
![]()
Controlerul
propus va avea forma ![]() unde
unde
![]() (3.102)
(3.102)
si
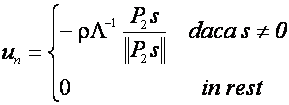 (3.103)
(3.103)
unde ![]() este o matrice care satisface conditia
este o matrice care satisface conditia
![]() (3.104)
(3.104)
si ![]() .
Ecuatia (3.102) poate fi scrisa ca
.
Ecuatia (3.102) poate fi scrisa ca
![]() (3.105)
(3.105)
unde
![]() (3.106)
(3.106)
![]() (3.107)
(3.107)
3.5.2 Metoda modelului de referinta
In aceasta abordare ideea este sa comparam iesirea sistemului nominal cu un model liniar. Informatia obtinuta de la eroarea de urmarire dintre iesirea sistemului nominal si modelul ideal este luata ca model al variabilei de stare. Se considera sistemul nominal
![]() (3.108)
(3.108)
Si presupunem ca modelul indeal este
![]() (3.109)
(3.109)
Unde ![]() si este un vector de intrare, adica semnalul
de referinta. Eroarea de urmarire este
si este un vector de intrare, adica semnalul
de referinta. Eroarea de urmarire este
![]() (3.110)
(3.110)
Daca
urmarirea este perfecta ![]() .
Obiectivul metodei modelului de referinta este sa proiectam un controler astfel
incat eroarea de urmarire sa fie zero. Presupunem ca perechea modelului de
referinta
.
Obiectivul metodei modelului de referinta este sa proiectam un controler astfel
incat eroarea de urmarire sa fie zero. Presupunem ca perechea modelului de
referinta ![]() este obtinuta din gainul controlerului,
este obtinuta din gainul controlerului, ![]() prin ecuatia
prin ecuatia
![]() (3.111)
(3.111)
si
![]() (3.112)
(3.112)
In lucrarea se propune ca structura controlerului sa fie de forma
![]() (3.113)
(3.113)
Consideram eroarea derivata data in ecuatia (3.110)
![]() (3.114)
(3.114)
Adaugand si
scazand ![]() la
ecuatia (3.114) rezulta
la
ecuatia (3.114) rezulta
![]() (3.115)
(3.115)
Pe baza
ecuatiei (3.115) un controler poate fi proiectat pentru a elimina termenii ![]() si
si ![]() din partea dreapta a ecuatiei. In primul rand
se defineste eroarea functiei de comutatie
din partea dreapta a ecuatiei. In primul rand
se defineste eroarea functiei de comutatie
![]() (3.116)
(3.116)
Care corespunde urmatorului hiperplan
![]() (3.117)
(3.117)
Deci in timpul unei miscari de alunecare ideale
![]() (3.118)
(3.118)
Diferentiind si substituind ecuatia (3.115) rezulta
![]() (3.119)
(3.119)
Presupunem
ca ![]() este nesingulara, rezulta
este nesingulara, rezulta
![]() (3.120)
(3.120)
Sistemul de ordin redus este dat de
![]() (3.121)
(3.121)
Substituind ecuatia (3.111) si (3.112) rezulta
![]() (3.122)
(3.122)
In timpul unei miscari de alunecare ideala ecuatia (3.122) se reduce la
![]() (3.123)
(3.123)
Daca
perechea ![]() este controlabila atunci matricea
este controlabila atunci matricea ![]() a hiperplanului poate fi proiectata folosind
oricare din metodele anterioare astfel incat
a hiperplanului poate fi proiectata folosind
oricare din metodele anterioare astfel incat ![]() si
si ![]() .
Se presupune un controler de forma (3.113) unde
.
Se presupune un controler de forma (3.113) unde
![]() (3.124)
(3.124)
si unde
![]() (3.125)
(3.125)
si
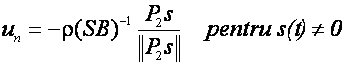 (3.126)
(3.126)
unde ![]() si satisface conditia
si satisface conditia
![]() (3.127)
(3.127)
Scalarul ![]() depinde de marimea incertitudinii si
depinde de marimea incertitudinii si ![]() este o matrice stabila.
este o matrice stabila.
3.6 Folosirea SMC in aplicatiile FTC
3.6.1 Robustete impotriva defectelor actuatorului
Daca in (2.1) defectele actuatorului intr-un sistem liniar pot fi reprezentate ca
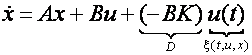 (3.128)
(3.128)
Unde ![]() si deci
si deci![]() sunt scalari
sunt scalari ![]()
Aceasta
reprezentare a defectului actuatorului de potriveste cu definitia pentru
incertitudini potrivite din subcapitolul 3.1.2. Cand ![]() actuatorul functioneaza perfect. Cand
actuatorul functioneaza perfect. Cand ![]() actuatorul are un anumit grad de defectiune. Cand
actuatorul are un anumit grad de defectiune. Cand ![]() actuatorul a cedat complet. Proprietatile de
robustete ale modului de alunecare impotriva defectelor actuatorului il fac un
candidat potrivit pentru FTC. Cativa cercetatori au studiat potentialul modului
de control al alunecarii in domeniul controlului reconfigurabil si in domeniul
FTC.
actuatorul a cedat complet. Proprietatile de
robustete ale modului de alunecare impotriva defectelor actuatorului il fac un
candidat potrivit pentru FTC. Cativa cercetatori au studiat potentialul modului
de control al alunecarii in domeniul controlului reconfigurabil si in domeniul
FTC.
3.6.2 Defectele actuatorului
In ciuda capacitatii sale de a manipula defecetele actuatorului fara a fi necesara reconfigurarea, nu poate face fata direct defectarii totala a actuatorului. In timpul defectarii totale a actuatorului un anumit tip de reconfigurare sau acomodare este necesara pentru a permite SMC sa faca fata defectarii acestuia. In anumite sisteme dublarea redundantei acuatorului este disponibila. In aceasta situatie controlerul modului de alunecare poate face fata defectarii totale prin simpla schimbare a semnalului de control catre dublura actuatoruluiu fara a fi nevoie de reconfigurare. Acest lucru este simplu de facut deoarece acelasi controler de iesire al modului de alunecare v-a fi in masura sa fie folosit de mai multe actuatoare.
Aceasta este totusi restrictionata la sistemele cu actuatoare redundante care sunt o copie fidela a originalului. In multe sisteme reale duplicarea nu este disponibila. Astfel sunt necesare alte instrumente ale sistemului care sa faca fata defectarii totale a actuatorului. Acest fapt ridica intrebarea daca si alte instrumente pot fi combinate cu controlul modului de alunecare pentru a face fata defectarii totale a actuatorului. Un potential candidat din lista metodelor FTC este CA. In sitemele de siguranta critice deja exista redundante disponibile. Aceste redundante pot fi gestionate intr-o buna modalitate de catre CA pentru atingerea mai multor obiective inclusiv reducerea consumului de carburant. In acest caz CA are abilitatea de a redistribui semanlele de control catre actuatoarele functionale.
Chiar mai bine, o combinatie intre proprietatile robuste ale SMC si capacitatile de realocare a controlului ale CA dau posibilitatea controlerelor simple si robuste sa faca fata defectelor fara reconfigurare. Aceasta permite unui singur controler sa lucreze in orice conditii.
Sistemul SMC pe un avion mare de transport
Pentru a imbunatatii siguranta aeronavelor mari de pasageri deja exista in literatura de spacialitate informatii despre FTC; fara a mentiona munca celor de la NASA cu privire la aeronavele controlate prin propulsie.Toate lucrarile descriu munca de cercetare asupra modelului B-747 bazat pe software-ul numit FTLAB747. In [80] un contoler LPV este propus pentru FTC, totusi este luat in considerare doar conrolul longitudinal. In [247] este luat in considerare atat controlul longitudinal cat si cel lateral dar este aplicat numai unui model liniar. Metodele modului de alunecare au fost aplicate unor prototipuri de aeronave de inalta performanta.
3.8 Concluzii
In acest capitol conceptul de proces de proiectare pentru ideile modului de alunecare au fost prezentate folosind ca exemplu un pendul. Au fost in special prezentate proprietatile de robustete impotriva incertitudinilor potrivite. Modificarea legii de control pentru a indeplinii cerintele de urmarire a fost de asemenea discutata. In final au fost prezentate avantajele si dezavantajele controlului modului de alunecare si cum pot fi ele aplicate la FTC.
CAPITOLUL 4
Controlul tolerant al defectelor aplicat unui avion civil de dimensiuni mari
4.1 Introducere
In acest capitol sistemele modului de alunecare pentru FTC sunt dezvoltate si aplicate unui avion. Sistemul de pe aeronava este un model B-747 care a fost folosi de catre alti cercetatori ca un test pentru evolutia lor. Un gain adaptiv este folosit in partea neliniara a legii de control care reactioneaza la aparitia unui defect si tinde sa tina functia de comutatie cat mai aproape de zero, deci incercand sa mentina performantele nominale de urmarire. Daca defectul total al unui actuator este detectat, un switch face trimitere la un back-up al suprafetei de control dar componenta liniara a legii de control ramane neschimbata.
Acest controler este testat in diferite scenarii ale defectelor actuatorului. Noutatea lucrarii din acest capitol este designul hiperplanului de alunecare care minimizeaza efectul incertitudinilor nepotrivite la miscarea de alunecare care decurg de de la defectul actuatorului si dezvoltarea unor sisteme adaptive simple pentru vectorul unitate neliniar. FTLAB B747 care ruleaza in MATLAB, a fost dezvoltat pentru studiul controlului tolerant la defecte si al sistemului FDI. Modelul neliniar de inalta fidelitate are 77 de stari care incorporeaza variabilele, senzori, actuatoare si aeromotoare dinamice. Toate suprafetele de control si dinamica motorului sunt modelate cu limite de pozitie.
4.2 Controlul tolerant al defectului actuatorului
Aceasta se va concentra pe proiectarea unui controler tolerant la defecte care sa faca fata defectarii actuatorului. Se considera sistemul liniar invariant in timp de ordinul n cu m intrari :
![]() (4.1)
(4.1)
Unde ![]() .
Ca si in (2.1) matricea k(t) este formata din functii scalare
.
Ca si in (2.1) matricea k(t) este formata din functii scalare ![]() care
satisface conditia
care
satisface conditia ![]() .
Acest model prezinta o scadere a eficientei pentru un tip particular de
actuator. Daca
.
Acest model prezinta o scadere a eficientei pentru un tip particular de
actuator. Daca ![]() actuatorul funtioneaza perfect. Daca
actuatorul funtioneaza perfect. Daca ![]() actuatorul are anumite defecte. Fara pierderea
generalitatii se presupune ca matricea de intrare
actuatorul are anumite defecte. Fara pierderea
generalitatii se presupune ca matricea de intrare ![]() are
gradul cel mai mare iar perechea
are
gradul cel mai mare iar perechea ![]() este
controlabila. Functia
este
controlabila. Functia ![]() este necunoscuta dar este delimitata si
reprezinta incertitudinea din sistem
este necunoscuta dar este delimitata si
reprezinta incertitudinea din sistem
![]() (4.2)
(4.2)
Unde ![]() sunt constante. Se ia in considerare numai
controlul longitudinal : toate starile laterale si directionale au fost
setate sa stearga valorile.
sunt constante. Se ia in considerare numai
controlul longitudinal : toate starile laterale si directionale au fost
setate sa stearga valorile.
Controlerul este proiectat pentru a obtine o buna urmarire a unghiului de zbor si a vitezei de curgere a aerului. Controlerul miscarii de alunecare nominala a fost proiectat folosind modelul liniar obtinut de la FTLAB B747.
Liniarizarea
a fost obtinuta in jurul unei conditii de operare de 300 tone, 184 m/s viteza
de curgere a aerului si o altitudine de 4000 de metri. Rezultatul este un model
de ordinul sase asociat cu unghiul de atac ![]() ,
viteza aerului
,
viteza aerului ![]() ,
unghiul de tangaj
,
unghiul de tangaj ![]() ,
altitudinea
,
altitudinea ![]() ,
si pozitia orizontala in lungul axei Pamantului
,
si pozitia orizontala in lungul axei Pamantului ![]() .
.
In scopul proiectarii nu au fost retinute decat primele patru stari si patru motoare individuale au fost agregate pentru a produce o singura intrare. Celelalte doua intrari reprezinta devierea profundorului si devierea stabilizatorului orizontal. In urmatoarele reprezentari spatiu-timp cele trei intrari au fost scalate individual ceea ce duce la :
 (4.3)
(4.3)
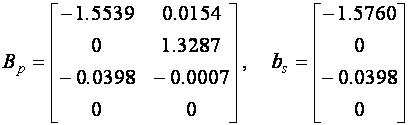 (4.4)
(4.4)
unde starile
reprezinta viteza de tangaj (rad/s), viteza de curgere a aerului (m/s), unghiul
de atac (rad), unghiul de tangaj (rad). Intrarile asociate cu ![]() sunt devierea profundorului si forta de
tractiune (N),
sunt devierea profundorului si forta de
tractiune (N), ![]() este
matricea distributiilor asociata cu stabilizatorul.
este
matricea distributiilor asociata cu stabilizatorul.
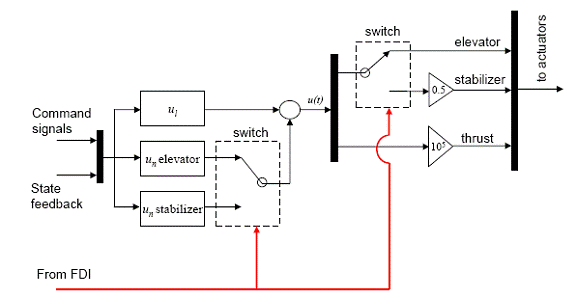
Fig.4.1
In timpul functionarii normale aeronava va fi controlata folosind
propulsia si profundorul, dar in cazul defectarii profundorului stabilizatorul
poate fi folosit ca back-up. In aceasta situatie ![]() va fi folosit ca sa inlocuiasca prima coloana
a lui
va fi folosit ca sa inlocuiasca prima coloana
a lui ![]() atunci cand controlerul de back-up a fost
activat. Cand implementam
controlerul la un model neliniar, un bloc gain este folosit pentru a recupera
semnalul trimis la actuator. Iesirea controlerului este urmatoarea
matrice :
atunci cand controlerul de back-up a fost
activat. Cand implementam
controlerul la un model neliniar, un bloc gain este folosit pentru a recupera
semnalul trimis la actuator. Iesirea controlerului este urmatoarea
matrice :
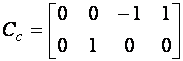 (4.5)
(4.5)
care
reprezinta unghiul de zbor (FPA) si viteza ![]() .
Modelul liniar va fi folosit pentru a proiecta controlerul care va fi descris
in continuare.
.
Modelul liniar va fi folosit pentru a proiecta controlerul care va fi descris
in continuare.
4.2.1 Proiectarea controlerului modului de alunecare
Actiunea
integrala va fi inclusa pentru a adauga o facilitate de urmarire pentru cele
doua iesiri controlate FPA si ![]() .
.
![]() (4.6)
(4.6)
unde
semnalul diferentiabil ![]() satisface
satisface
![]() (4.7)
(4.7)
Cu ![]() o matrice stabila,
o matrice stabila, ![]() vector constant.
vector constant.
![]()
![]() (4.8)
(4.8)
unde
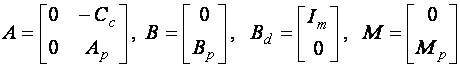 (4.9)
(4.9)
Deoarece
perechea ![]() este
controlabila, daca
este
controlabila, daca ![]() nu are nici un zero invariant in origine
atunci (A,B) este controlabila. Definim
nu are nici un zero invariant in origine
atunci (A,B) este controlabila. Definim
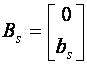 (4.10)
(4.10)
desi![]() nu
apare in ecuatia (4.8) reprezinta matricea de distributie asociata ecuatiei
(4.8) cand stabilizatorul este folosit ca back-up. Definim
nu
apare in ecuatia (4.8) reprezinta matricea de distributie asociata ecuatiei
(4.8) cand stabilizatorul este folosit ca back-up. Definim
![]() (4.11)
(4.11)
unde ![]() este
de cel mai mare rang. Daca o lege de control care forteaza traiectoria buclei
inchise sa ramana pe suprafata S(t)=0 atunci o miscare de alunecare ideala a
fost obtinuta. Presupunem ca matricea S este proiectata astfel incat matricea
patratica SB este nesingulara. Rezulta ca miscarea de alunecare ideala este
data de
este
de cel mai mare rang. Daca o lege de control care forteaza traiectoria buclei
inchise sa ramana pe suprafata S(t)=0 atunci o miscare de alunecare ideala a
fost obtinuta. Presupunem ca matricea S este proiectata astfel incat matricea
patratica SB este nesingulara. Rezulta ca miscarea de alunecare ideala este
data de
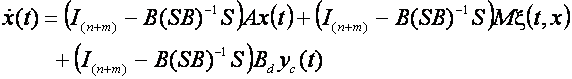
pentru ![]() si
si ![]() .
.
Daca ![]() atunci
atunci ![]() apartine spatiului matricei
apartine spatiului matricei ![]() .
.
Si miscarea de alunecare este independenta de incertitudini.
Cateva
abordari au fost propuse pentru proiectarea lui S inclusiv minimizarea
cuadrica. In plus fara pierderea generalitatii, suprafata poate fi proiectata
intotdeauna astfel incat ![]() .
Legea de control propusa are doua componente, una liniara si una neliniara.
.
Legea de control propusa are doua componente, una liniara si una neliniara.
![]() (4.13)
(4.13)
unde componenta liniara este
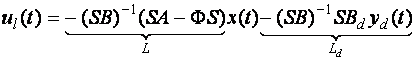 (4.14)
(4.14)
unde ![]() este
o matrice proiectata, si
este
o matrice proiectata, si ![]() este componeneta discontinua care este functie
de s. structura legii de control propuse este de forma
este componeneta discontinua care este functie
de s. structura legii de control propuse este de forma
![]() (4.15)
(4.15)
unde ![]() sunt constante pozitive,
sunt constante pozitive, ![]() este componenta lui
este componenta lui ![]() este componenta lui
este componenta lui ![]() .
.
![]() este definit ca :
este definit ca :
![]() (4.16)
(4.16)
unde
![]() (4.17)
(4.17)
si constantele ![]() sunt din (4.2). Variabilele
sunt din (4.2). Variabilele ![]() sunt gainuri care variaza conform cu :
sunt gainuri care variaza conform cu :
![]()
![]() (4.18)
(4.18)
unde ![]() sunt
constante pozitive. Functia
sunt
constante pozitive. Functia ![]() este o functie neliniara
este o functie neliniara
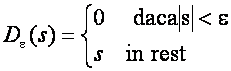 (4.19)
(4.19)
unde ![]() este un scalar pozitiv. Daca apare un defect
care incepe sa faca miscarea de alunecare sa se degradeze astfel incat sa
evolueze in afara limitelor
este un scalar pozitiv. Daca apare un defect
care incepe sa faca miscarea de alunecare sa se degradeze astfel incat sa
evolueze in afara limitelor ![]() ,
apoi coeficientii dinamici
,
apoi coeficientii dinamici ![]() cresc in magnitudine pentru a forta starile
inapoi in stratul limita. Alegerea parametrilor de proiectare
cresc in magnitudine pentru a forta starile
inapoi in stratul limita. Alegerea parametrilor de proiectare ![]() depinde de performantele buclei inchise si au
nevoie de iteratii de proiectare. In general
depinde de performantele buclei inchise si au
nevoie de iteratii de proiectare. In general ![]() trebuie sa fie ales astfel incat gainul
nominal al componentei neliniare a legii de control (4.15) sa asigure ca
alunecarea se petrece intr-un sistem fara defecte. Parametrul
trebuie sa fie ales astfel incat gainul
nominal al componentei neliniare a legii de control (4.15) sa asigure ca
alunecarea se petrece intr-un sistem fara defecte. Parametrul ![]() este ales sa fie mic sa formeze un strat
limita deasupra lui S. acesta dicteaza cat de sensibil este gainul adaptiv
este ales sa fie mic sa formeze un strat
limita deasupra lui S. acesta dicteaza cat de sensibil este gainul adaptiv ![]() la schimbarile s(t). Gainul
la schimbarile s(t). Gainul ![]() dicteaza rata la care
dicteaza rata la care ![]() creste in reactie la defecte. O valoare mare
pentru
creste in reactie la defecte. O valoare mare
pentru ![]() indica o crestere rapida a lui
indica o crestere rapida a lui ![]() .
Pe de alta parte
.
Pe de alta parte ![]() dicteaza rata la care
dicteaza rata la care ![]() descreste pana la gainul nominal
descreste pana la gainul nominal ![]() cand defectul a fost rectificat.
cand defectul a fost rectificat.
Teorema 1:Se
considera sistemulul cu erori reprezentat de (4.8) cu legea de control
(4.15) ; apoi fiecare componenta ![]() ramane delimitata iar starile de comutatie
ramane delimitata iar starile de comutatie ![]() intra in stratul limita din jurul lui S in
timp finit.
intra in stratul limita din jurul lui S in
timp finit.
Demonstratie.
Se considera ![]() . Presupunem
. Presupunem ![]() . Rezulta
. Rezulta
![]()
Unde s-a
presupus ![]() si
si ![]() sunt scalari pozitivi. De aici
sunt scalari pozitivi. De aici
![]() (4.21)
(4.21)
Folosind
(4.17) si ![]() rezulta
rezulta
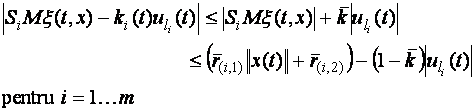 (4.22)
(4.22)
Definim scalarul
![]() (4.23)
(4.23)
si componenta funtiei Lyapunov
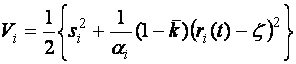 (4.24)
(4.24)
unde ![]() este un scalar pozitiv din (4.18). Derivand
rezulta ca
este un scalar pozitiv din (4.18). Derivand
rezulta ca
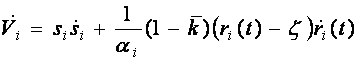 (4.25)
(4.25)
Substituind
(4.16), (4.18), (4.21), (4.22) in (4.25) si notand ![]() rezulta
rezulta
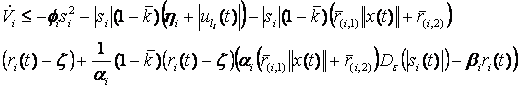
Daca ![]() atunci
atunci ![]()
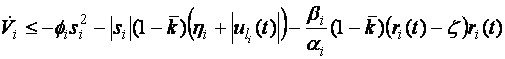 (4.27)
(4.27)
![]() Folosind (4.27) si (4.23) rezulta
Folosind (4.27) si (4.23) rezulta
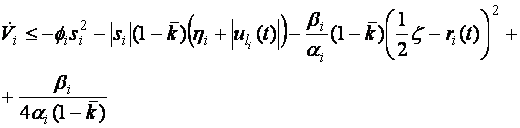
Dezvoltand
termenul din partea dreapta a ecuatiei (4.28) rezulta (4.27). Daca ![]() atunci
atunci ![]() .
.
![]() sunt
parametri de proiectare, si daca sunt alesi sa satisfaca conditia
sunt
parametri de proiectare, si daca sunt alesi sa satisfaca conditia
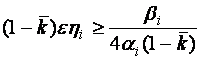 (4.29)
(4.29)
Atunci
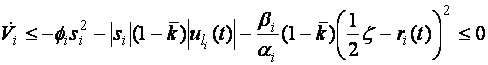 (4.30)
(4.30)
Daca ![]() atunci
atunci ![]() si substituind in (4.26) rezulta
si substituind in (4.26) rezulta
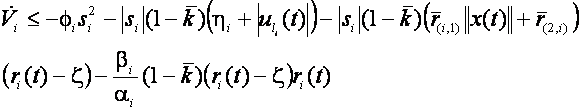
![]() si de
aici pentru
si de
aici pentru ![]() si
si ![]() rezulta
rezulta ![]() .
Definim
.
Definim
![]() (4.32)
(4.32)
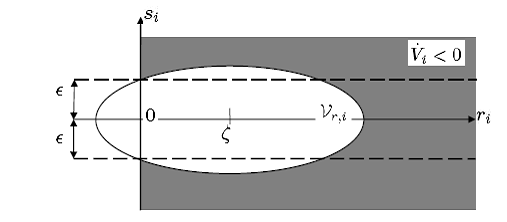
Fig 4.2
Observatii :
daca ![]() si
si ![]() atunci alunecarea ideala poate fi garantata
dupa cum rezulta din (4.27). asta inseamna ca alunecarea ideala poate fi
obtinuta si mentinuta in timp finit. Aceasta scheme adaptiva are dezavantajul in practica
deoarece gainurile
atunci alunecarea ideala poate fi garantata
dupa cum rezulta din (4.27). asta inseamna ca alunecarea ideala poate fi
obtinuta si mentinuta in timp finit. Aceasta scheme adaptiva are dezavantajul in practica
deoarece gainurile ![]() pot deveni nedelimitate in prezenta zgomotului
.
pot deveni nedelimitate in prezenta zgomotului
.
Gainul adaptiv functioneaza ca o masura a severitatii defectelor
actuatorului. Odata ce gainul adaptiv ![]() din (4.16) depaseste o valoare maxima
predeterminata
din (4.16) depaseste o valoare maxima
predeterminata ![]() un
defect sever este declarat si o strategie de control de back-up poate fi
initiata
un
defect sever este declarat si o strategie de control de back-up poate fi
initiata
Din (4.23),![]() devine infinit. In cazul unui defect total o strategie alternativa de control
trebuie initiata.
devine infinit. In cazul unui defect total o strategie alternativa de control
trebuie initiata.
4.2.2 Proiectarea hiperplanului modului de alunecare
Primul pas in proiectarea controlerului modului de
alunecare este alegerea matricii suprafetei de alunecare S. O metoda este
costul functiei. Metoda de proiectare abordata este descrisa in special pentru
sistemele de aviatie. In primul rand consideram problema proiectarii matricei S
a suprafetei de alunecare pentru sistemul nominal liniar asociat cu (4.24).
Presupunem ca nu exista defecte k(t)=0si
nu exista nici o referinta ceruta ![]() .
De asemenea in scopul proiectarii se ignora termenul de incertitudine. Pentru
sistemul liniar nominal se ia in considerare problema minimizarii indicelui de
performanta cuadrica.
.
De asemenea in scopul proiectarii se ignora termenul de incertitudine. Pentru
sistemul liniar nominal se ia in considerare problema minimizarii indicelui de
performanta cuadrica.
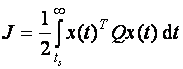 (4.33)
(4.33)
unde Q este simetric pozitiv, ![]() reprezinta timpul la care miscarea de
alunecare incepe. Se defineste schimbarea de coordonate
reprezinta timpul la care miscarea de
alunecare incepe. Se defineste schimbarea de coordonate
![]() (4.34)
(4.34)
unde ![]() este o matrice ortogonala
este o matrice ortogonala
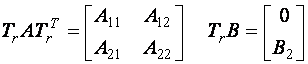
unde ![]() .
Rezulta
.
Rezulta
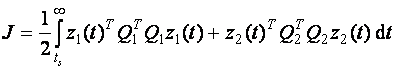 (4.35)
(4.35)
unde ![]()
![]() (4.36)
(4.36)
unde 'controlul virtual'![]() satisface conditia
satisface conditia
![]() (4.37)
(4.37)
Aceasta reprezinta ecuatia hiperplanului![]() . Costul optimal este dat de
. Costul optimal este dat de ![]() unde
unde ![]() este solutia ecuatiei Riccati
este solutia ecuatiei Riccati
![]() (4.38)
(4.38)
unde ![]() este valoarea componentei de stare
este valoarea componentei de stare ![]() la timpul la care alunecarea are loc si
alegerea optima este
la timpul la care alunecarea are loc si
alegerea optima este ![]() . Aceasta problema poate fi reprezentata ca o
optimizare LMI. Minimizarea
. Aceasta problema poate fi reprezentata ca o
optimizare LMI. Minimizarea ![]() este
este
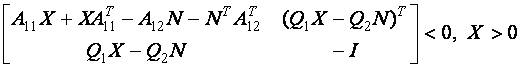
unde ![]() In cazul unui back-up matricea intrarilor
distribuite este perturbata de schimbarile din actuator. Matricea noilor
intrari distribuite
In cazul unui back-up matricea intrarilor
distribuite este perturbata de schimbarile din actuator. Matricea noilor
intrari distribuite ![]() este compusa din inlocuirea primei coloane a
lui B in (4.9) asociata cu profundorul, cu
este compusa din inlocuirea primei coloane a
lui B in (4.9) asociata cu profundorul, cu ![]() in (4.10) asociata cu stabilizatorul. In forma
regulata coordonatele sunt
in (4.10) asociata cu stabilizatorul. In forma
regulata coordonatele sunt
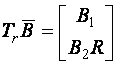
unde ![]() si
si ![]() . Obtinerea unei miscari de alunecare poate fi
mentinuta cu noile actuatoare in coordonate regulate, apoi
. Obtinerea unei miscari de alunecare poate fi
mentinuta cu noile actuatoare in coordonate regulate, apoi
![]() (4.40)
(4.40)
In loc de (4.36) si (4.37) unde ![]() este semnalul de control echivalent necesar
mentinerii miscarii de alunecare pe S si
este semnalul de control echivalent necesar
mentinerii miscarii de alunecare pe S si ![]() reprezinta randurile 'n' de sus ale lui
reprezinta randurile 'n' de sus ale lui ![]() .
Semnalul
.
Semnalul ![]() v-a fi o functie a starilor
v-a fi o functie a starilor ![]() si v-a include efectele suplimentare
nepotrivite ale perturbatiilor rezultate in urma defectului. Obiectivul este
minimizarea efectului
si v-a include efectele suplimentare
nepotrivite ale perturbatiilor rezultate in urma defectului. Obiectivul este
minimizarea efectului ![]() la valoarea nominala a sistemului in ecuatia
(4.40).
la valoarea nominala a sistemului in ecuatia
(4.40).
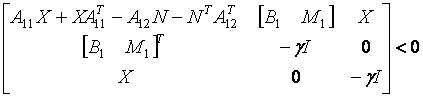 (4.41)
(4.41)
In ansamblu problema optimizarii folosita aici este
minimizarea lui ![]() .
.
 (4.42)
(4.42)
Matricea 'Z' este o 'variabila statatoare' care
satisface conditia ![]() si urma(Z) limiteaza urma(
si urma(Z) limiteaza urma(![]() ).
).
![]() poate fi aflat folosind standardul LMI.
Matricea care determina hiperplanul este calculata ca
poate fi aflat folosind standardul LMI.
Matricea care determina hiperplanul este calculata ca ![]() si
rezulta
si
rezulta
![]() (4.43)
(4.43)
Matricea nonsingulara ![]() este
aleasa pentru a indeplini conditia
este
aleasa pentru a indeplini conditia ![]() .
.
Capitolul 5
Reconstructia defectelor modului de alunecare si controlul tolerant al defectelor senzorilor
In acest capitol se vor demonstra capabilitatile observerelor modului de alunecare pentru robustetea senzorilor la estimarea defectelor pe acelasi model neliniar B-747. In acest capitol semnalele despre defectele de la senzori vor fi folosite la obtinerea unor senzori toleranti la defecte, deoarece semnalele masurate de la senzori pot fi corectate inainte de a fi folosite de catre controler. Aceasta elimina nevoia pentru reconfigurarea controlerului si elimina cerintele suplimentare pentru senzori redundanti in sistem.
5.1 Introducere
Observerele modului de alunecare au propriile lor caracteristici unice care sunt benefice pentru FDI si pentru manipularea defectelor senzorilor. Din punct de vedere al defectelor senzorilor SMC are acelasi dezavantaj ca si cele mai multe controlere clasice adica nu poate face fata defectelor senzorilor in mod direct. Un foarte bun controler proiectat v-a deveni unul foarte prost atunci cand se defecteaza, deoarece controlerul v-a urmari in mod 'fidel' masuratorile gresite ale senzorului defect. In aceasta lucrare nu v-a fi luata in considerare defectarea totala a senzorilor deoarece in avionica senzorii vitali prezinta dubla sau chiar tripla redundanta. In cazul defectarii totale a senzorilor, un sistem de vot poate fi folosit pentru a elimina senzorul defect si deci numai senzorii buni vor fi folositi pentru controlul cu feedback. Anumite tipuri de defectiuni ale senzorilor nu afecteaza stabilitatea avionului dar altele micsoreaza performantele si afecteaza stabilitatea.
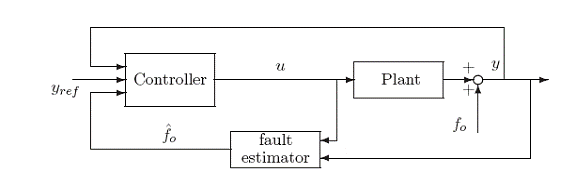
Fig 5.1
5.2 Observere ale modului de alunecare pentru FDI
Ideea este sa proiectam gainurile observerului astfel incat suprafata de alunecare este atinsa si mentinuta astfel incat eroarea dintre sistem si starea observerului este zero. Primul design al observerului modului de alunecare folosea in mod obisnuit un concept bazat pe FDI. Ideea a fost de a asigura ca miscarea de alunecare a fost rupta atunci cand un defect aparea in sistem si un semnal rezidual era generat continand informatii despre defect.
Nu numai ca aceste abordari de proiectare au abilitatea de a detecta si izola surza defectului dar asigura si informatii care por fi folosite in special pentru reconfigurarea controlerului. Din punct de vedere al FTC disponibilitatea unui semnal de reconstructie al defectului, inseamna ca defectele senzorului pot fi corectate inainte ca semnalul sa fie folosit de controler si severitatea defectului unui actuator poate fi estimata ceea ce este benefic pentru reconfigurarea controlerului .
Senzorul FTC va fi folosit la estimarea defectelor pentru a corecta semnalele 'corupte', astfel evitand in mod direct reconfigurarea controlerului.
5.3 Obserever al modului de alunecare
Urmatorul subcapitol va prezenta pe scurta o clasa de obsevere ale modului de alunecare. Cele prezentate aici au evoluat din observere Utkin si Walcott-Zak si se numesc observere Edwards-Spurgeon . Se considera urmatorul sistem neliniar
![]() (5.1)
(5.1)
![]() (5.2)
(5.2)
unde ![]() .
.
![]() (5.3)
(5.3)
unde ![]() este un scalar cunoscut si
este un scalar cunoscut si ![]() .
Se propune ca pentru proiectare, sistemul sa fie transformat intr-un observer
de forma canonica prin folosirea matricii de transformare
.
Se propune ca pentru proiectare, sistemul sa fie transformat intr-un observer
de forma canonica prin folosirea matricii de transformare![]() si sitemul poate fi reprezentat
si sitemul poate fi reprezentat
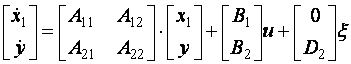 (5.4)
(5.4)
unde ![]() . In noul sistem de coordonate
matricea iesirilor distribuite este:
. In noul sistem de coordonate
matricea iesirilor distribuite este:
![]() (5.5)
(5.5)
Un observer asociat cu acest sistem are forma
![]() (5.6)
(5.6)
unde
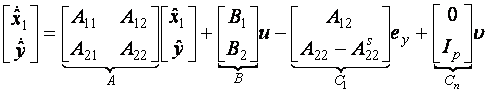 (5.7)
(5.7)
![]() este o
matrice stabila. Cantitatea
este o
matrice stabila. Cantitatea ![]() este
iesirea estimata a erorii si
este
iesirea estimata a erorii si ![]() se defineste ca:
se defineste ca:
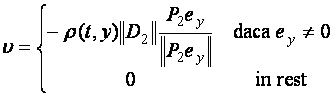 (5.8)
(5.8)
Matricea ![]() este o matrice a.s.p.d. si satisface ecuatia
Lyapunov
este o matrice a.s.p.d. si satisface ecuatia
Lyapunov
![]() (5.9)
(5.9)
Scalarul ![]() in (5.8) depinde de marimea incertitudinii si
este orice functie care satisface conditia :
in (5.8) depinde de marimea incertitudinii si
este orice functie care satisface conditia :
![]() (5.10)
(5.10)
unde ![]() este un scalar pozitiv. Suprafata de alunecare
este hiperplanul reprezentat de
este un scalar pozitiv. Suprafata de alunecare
este hiperplanul reprezentat de
![]() (5.11)
(5.11)
unde ![]()
![]() .
Eroarea estimata a starii sistemului asociata cu
.
Eroarea estimata a starii sistemului asociata cu ![]() si
si 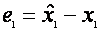 devine
devine
 (5.12)
(5.12)
Conditia necesara si suficienta pentru existenta formei canonice (5.4) este data de :
![]()
orice
zero invariant al ![]() trebuie sa apartina lui
trebuie sa apartina lui![]()
![]() .
.
In coordonatele originale obseverul din ecuatiile (5.6), (5.7) poate fi scris ca:
![]() (5.13)
(5.13)
Gainurile observerului si parametrii acestuia sunt dati de
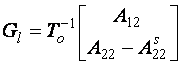 (5.14)
(5.14)
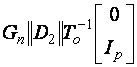 (5.15)
(5.15)
 (5.16)
(5.16)
unde ![]() este matricea de transformare folosita pentru
a obtine observerul in forma canonica in (5.4). Se poate demonstra ca:
este matricea de transformare folosita pentru
a obtine observerul in forma canonica in (5.4). Se poate demonstra ca:
![]()
si zerourile invariante ![]() sunt un subset al lui
sunt un subset al lui ![]() .
Pentru o alegere corecta a lui
.
Pentru o alegere corecta a lui ![]() o miscare de alunecare se obtine pe
o miscare de alunecare se obtine pe ![]() in timp finit.
in timp finit.
5.4 Observerul Edwards-Spurgeon pentru reconstructia defectelor
Acest subcapitol va descrie una dintre proprietatile interesante ale observerului modului de alunecare care va fi folosit pentru estimarea defectului bazat pe conceptul echivalent 'eroarea iesirii injectate' care a devenit baza pentru senzorul FTC folosit in acest capitol. Se considera sistemul liniar nominal supus la defecte descris de ecuatia
![]() (5.17)
(5.17)
![]() (5.18)
(5.18)
S-a propus ca matricele ![]() sunt
cunoscute. Semnalele
sunt
cunoscute. Semnalele ![]() reprezinta defectul actuatorului respectiv
senzorului dar se presupune ca numai
reprezinta defectul actuatorului respectiv
senzorului dar se presupune ca numai ![]() si
si ![]() sunt masurabile. Presupunem ca a fost
proiectat un observer cu structura data de ecuatia (5.13). Producerea unei
miscari de alunecare poate fi atinsa iar estimarile
sunt masurabile. Presupunem ca a fost
proiectat un observer cu structura data de ecuatia (5.13). Producerea unei
miscari de alunecare poate fi atinsa iar estimarile ![]() pot fi
calculate prin aproximarea controlului echivalent.
pot fi
calculate prin aproximarea controlului echivalent.
Reconstructia intrarilor defecte
Se considera cazul in care ![]() In timpul miscarii de alunecare
In timpul miscarii de alunecare ![]() .
Deci partitia de jos a ecuatiei (5.12) poate fi scrisa ca :
.
Deci partitia de jos a ecuatiei (5.12) poate fi scrisa ca :
![]() (5.19)
(5.19)
unde ![]() este iesirea echivalenta de eoare injectata
necesara mentinerii alunecarii. Deoarece
este iesirea echivalenta de eoare injectata
necesara mentinerii alunecarii. Deoarece ![]() este stabila din constructie si
este stabila din constructie si ![]() rezulta
rezulta
![]() (5.20)
(5.20)
Semnalul ![]() este un semnal discontinuu si deci trebuie
folosita o aproximare pentru a recupera injectia echivalenta.
este un semnal discontinuu si deci trebuie
folosita o aproximare pentru a recupera injectia echivalenta.
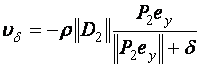 (5.21)
(5.21)
unde ![]() este un scalar pozitiv. Deoarece
este un scalar pozitiv. Deoarece ![]() rezulta din (5.20) ca
rezulta din (5.20) ca
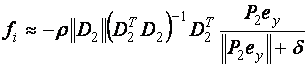 (5.22)
(5.22)
Partea din dreapta a ecuatiei de mai sus depinde numai
de ![]() si deci poate fi calculata online si o
aproximare pentru
si deci poate fi calculata online si o
aproximare pentru ![]() poate fi obtinuta in timp real.
poate fi obtinuta in timp real.
Reconstructia iesirilor defecte
Se considera cazul in care ![]() Deoarece iesirea sistemului este reprezentata de
ecuatia (5.18) rezulta
Deoarece iesirea sistemului este reprezentata de
ecuatia (5.18) rezulta
![]() (5.23)
(5.23)
Folosind aceasta ecuatie noua eroare estimata a starii sistemului in forma canonica din observerul (5.4) este data de ecuatia
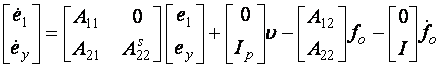 (5.24)
(5.24)
unde ![]() apar ca
perturbatii. Prin urmare in scopul mentinerii alunecarii gainul neliniar
apar ca
perturbatii. Prin urmare in scopul mentinerii alunecarii gainul neliniar![]() in (5.16) trebuie sa fie suficient de mare
pentru a invinge efectul perturbatiilor generate de
in (5.16) trebuie sa fie suficient de mare
pentru a invinge efectul perturbatiilor generate de ![]() . In timpul alunecarii
. In timpul alunecarii ![]() si deci partitia de jos a ecuatiei (5.24)
devine
si deci partitia de jos a ecuatiei (5.24)
devine
![]() (5.25)
(5.25)
Cand dinamica miscarii de alunecare este rapida,din partitia de sus a ecuatiei (5.24) rezulta
![]() (5.26)
(5.26)
Cand iesirea
defecta variaza lent astfel incat ![]() ,
apoi substituind partea de sus si inlocuind-o in (5.25) rezulta
,
apoi substituind partea de sus si inlocuind-o in (5.25) rezulta
![]() (5.27)
(5.27)
Ca si in cazul reconstructiei actuatorului defect semnalul ![]() poate fi calculat online folosind aproximarea
poate fi calculat online folosind aproximarea ![]() data in (5.21). Daca
data in (5.21). Daca ![]() este
nesingulara rezulta
este
nesingulara rezulta
![]() (5.28)
(5.28)
Observatie :
Metoda de mai sus nu a inclus nici o metoda de incertitudine de modelare in analiza sa. Aici ideea a fost de a oferi o simpla analiza asupra modului de alunecare al observerelor si cum pot fi folosite pentru reconstructia defectelor(fig 5.2). Metoda de mai sus a fost imbunatatita pentru aplicatii robuste folosind formularea LMI.
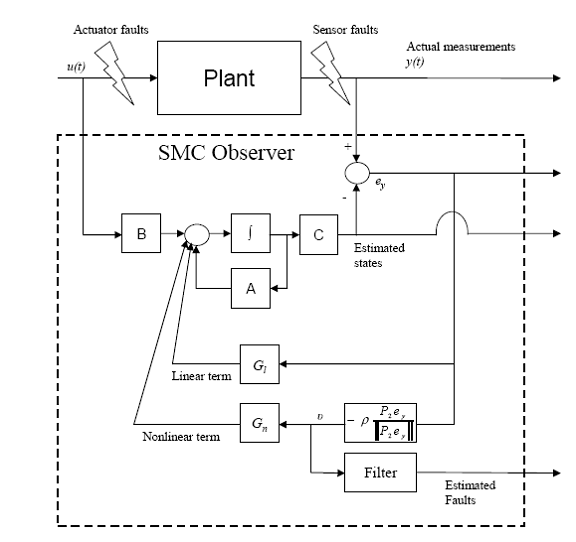
Fig 5.2
Analiza controlerului tolerant la defectele senzorilor in bucla inchisa.
In urmatorul subcapitol va fi prezentata ideea folosirii semnalelor de reconstructie a defectelor ca un mod de a obtine toleranta la defecte atunci cand acestea apar. In urmatorea subsectiune reconstructia defectelor se va baza pe metode robuste.
S-a propus ca masuratorile defectului sunt disponibile. Aici a fost luata in considerare posibilitatea ca starea masurata sa fie gresita. Aici se presupune ideea folosirii observerelor modului de alunecare pentru reconstructia semnalelor defecte si folosirea acestor semnale pentru corectarea valorilor masurate inainte de a fi folosite in legea de control.
Preliminarii
Se considera un sistem dinamic incert afectat de defectiunea senzorilor descrisi de ecuatiile
![]() (5.29)
(5.29)
![]() (5.30)
(5.30)
In (5.30) s-a presupus ca toate starile sunt disponibile masuratorilor.
Presupunem ca matricea ![]() are rang complet pe coloana si ca functia
are rang complet pe coloana si ca functia ![]() este cunoscuta dar delimitata astfel incat
este cunoscuta dar delimitata astfel incat
![]() (5.31)
(5.31)
unde ![]() este o
functie cunoscuta. Semnalul
este o
functie cunoscuta. Semnalul ![]() reprezinta defectul senzorului si
reprezinta defectul senzorului si ![]() reprezinta matricea de distributie care indica
care masuratori ale senzorilor nu sunt bune si sunt predispusi la defecte.
reprezinta matricea de distributie care indica
care masuratori ale senzorilor nu sunt bune si sunt predispusi la defecte.
Observatie : In ipoteza ca numai anumiti senzori sunt predispusi la defectiuni este o limitare. Cu toate acestea in situatii practice anumiti senzori pot fi mai vulnerabili la defecte sau pot fi mai sensibili din constructie decat altii. De asemenea anumiti senzori cheie pot avea back-up si deci in esenta un semnal fara erori poate fi asumat de un anumit subset de senzori.
Scopul este
proiectarea unor observere pentru modul de alunecare pentru a reconstrui
defectele ![]()
![]() .
.
Se considera
noua stare![]() care este versiunea filtrata a semnalului
care este versiunea filtrata a semnalului ![]() din ecuatia (5.30).
din ecuatia (5.30).
![]() (5.32)
(5.32)
unde![]() este o matrice stabila. Din ecuatiile (5.29) si (5.32) rezulta un sistem de
ordinul
este o matrice stabila. Din ecuatiile (5.29) si (5.32) rezulta un sistem de
ordinul ![]() cu starea
cu starea ![]() de forma
de forma
![]() (5.33)
(5.33)
![]() (5.34)
(5.34)
Din (5.33),(5.34) rezulta un observer al modului de alunecare de forma
![]() (5.35)
(5.35)
In (5.35) eroarea discontinua a iesirii termenului injectat este
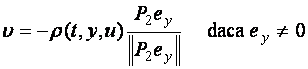 (5.36)
(5.36)
unde ![]() este eroarea estimata a iesirii si
este eroarea estimata a iesirii si![]() este o matrice definitra simetric pozitiva. Matricea
este o matrice definitra simetric pozitiva. Matricea ![]()
este gainul
observerului folosit pentru a face ![]() stabila si
stabila si ![]() trebuie aleasa pentru a asigura valorile
nonzero ale matricii
trebuie aleasa pentru a asigura valorile
nonzero ale matricii ![]() .
.
Un observer de forma (5.35) si (5.36) exista numai daca :
- ![]()
- nici un
zero invariant al ![]() nu apartine
nu apartine ![]()
Se poate
demonstra ca daca sistemul este stabil in bucla deschisa aceste conditii pot fi
intotdeauna indeplinite. Pentru o alegere potrivita a lui ![]() in (5.36) care trebuie sa limiteze
incertitudinile si supremul lui
in (5.36) care trebuie sa limiteze
incertitudinile si supremul lui ![]() din (5.31) si se poate demonstra ca o miscare
de alunecare ideala are loc pe
din (5.31) si se poate demonstra ca o miscare
de alunecare ideala are loc pe ![]() in timp finit unde
in timp finit unde ![]() este eroarea de stare estimata
este eroarea de stare estimata ![]() .
In timpul miscarii ideale de alunecare
.
In timpul miscarii ideale de alunecare ![]() si semnalul discontinu
si semnalul discontinu ![]() trebuie sa ia in medie o valoare care sa
compenseze pe
trebuie sa ia in medie o valoare care sa
compenseze pe ![]() si
si ![]() incat sa mentina alunecarea. Cantitatea medie
notata cu
incat sa mentina alunecarea. Cantitatea medie
notata cu ![]() se refera la termenul echivalent al erorii de
iesire injectata. Semnalul
se refera la termenul echivalent al erorii de
iesire injectata. Semnalul ![]() poate fi aproximat cu orice grad de acuratete
si se calculeaza ca
poate fi aproximat cu orice grad de acuratete
si se calculeaza ca
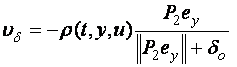 (5.37)
(5.37)
unde ![]() este un scalar pozitiv. Se considera semnalul
de reconstructie al erorii ca
este un scalar pozitiv. Se considera semnalul
de reconstructie al erorii ca
![]() (5.38)
(5.38)
![]() (5.39)
(5.39)
unde ![]() este matricea functiilor de transfer care
depinde de matricile sistemului
este matricea functiilor de transfer care
depinde de matricile sistemului ![]() ,matricea
observerului
,matricea
observerului ![]() si matricea de greutate
si matricea de greutate ![]() .
.
Minimizarea
efectului ![]() la reconstructia
la reconstructia ![]() se face prin minimizarea
se face prin minimizarea ![]() intre
intre ![]() si
si ![]() .
In acest capitol
.
In acest capitol
![]() (5.40)
(5.40)
unde ![]() este un scalar pozitiv si
este un scalar pozitiv si ![]() iar matricea
iar matricea ![]() este o matrice Lyapunov pentru eroarea
estimata a starii sistemului. In figura 5.3 iesirea sistemului FDI este eroarea estimata
este o matrice Lyapunov pentru eroarea
estimata a starii sistemului. In figura 5.3 iesirea sistemului FDI este eroarea estimata ![]() a senzorului.
a senzorului.
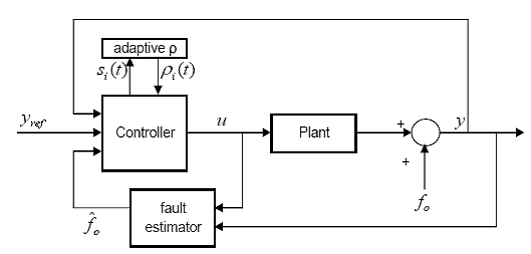
Fig 5.3
Analiza in bucla inchisa
In acest
capitol valoarea estimata a defectului senzorului ![]() v-a fi folosita pentru a corecta semnalul de
iesire astfel incat
v-a fi folosita pentru a corecta semnalul de
iesire astfel incat ![]() v-a fi iesirea unui ' senzor virtual' care va
fi folosit in legea de control pentru a genera semnalul
v-a fi iesirea unui ' senzor virtual' care va
fi folosit in legea de control pentru a genera semnalul ![]() .
Presupunem ca iesirea corectata este data de
.
Presupunem ca iesirea corectata este data de ![]() rezulta
rezulta
![]() (5.41)
(5.41)
Deasemenea starile integrale din (4.6) sunt corectate
![]() (5.42)
(5.42)
Daca ![]() rezulta
rezulta
 (5.43)
(5.43)
Din proiectare
![]()
In timpul unei miscari de alunecare daca folosim ![]() in loc de
in loc de ![]()
![]() rezulta
rezulta ![]()
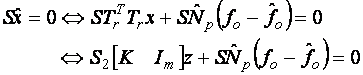 (5.44)
(5.44)
Din (5.44) in timpul unei miscari de alunecare
![]() (5.45)
(5.45)
In consecinta din (5.43) miscarea de alunecare de ordin redus este condusa de
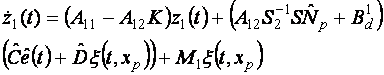 (5.46)
(5.46)
![]() (5.47)
(5.47)
Presupunem ca ![]() si deci
si deci
![]()
Din (5.45)rezulta ca
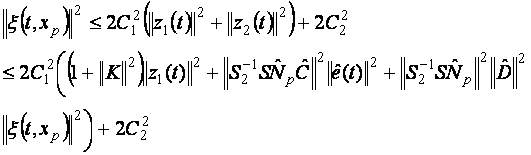
Daca
![]()
Inseamna ca
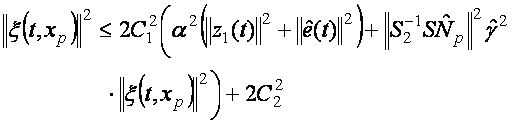 (5.48)
(5.48)
Rearanjand ecuatia (5.48) rezulta
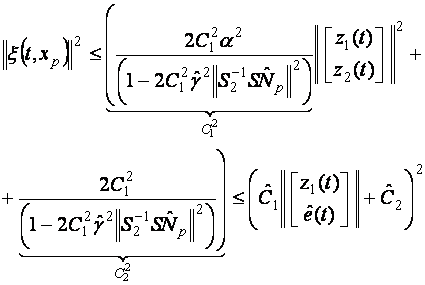 (5.49)
(5.49)
5.8 Concluzii
Acest capitol a introdus conceptul de observer al modului de alunecare si a subliniat capabilitatile si beneficiile observerelor modului de alunecare ca un mijloc de reconstructie al erorilor si un control tolerant al defectelor senzorilor. Cele mai multe rezultate existente in literatura de specialitate pentru avionul civil B-747, folosind FTLAB-747, s-au axat pe defectarea actuatorului sau existenta unor parametrii eronati. Acest capitol a prezentat reconstructia unui senzor defect si un sistem de control tolerant al senzorului defect. Deasemenea este prezentata functionarea sistemului in prezenta zgomotului.
Capitolul 6.
Controlul tolerant la defecte folosind modurile de alunecare cu alocarea controlului online
6.1 Introducere
In cele mai multe sisteme critice de siguranta ca de exemplu avioanele moderne exista redundanta a actuatorului. Aceasta da libertatea de a proiecta sisteme FTC pentru a mentine stabilitatea si performante acceptabile in timpul defectelor. CA este o abrodare pentru a gestiona redundanta actuatorului pentru diferite strategii de control care sa faca fata defectelor actuatorului.
Beneficiile CA folosite ca mijloc pentru FTC este acela ca structura controlerului nu trebuie sa fie reconfigurata in cazul defectelor, CA putand sa faca fata direct defectarii totale a actuatorului, redistribuind semnalele de control.
In acest capitol se v-a folosi o combinatie intre SMC si CA pentru a obtine FTC. Sistemele propuse au fost testate in simulari pe un model de avion care a fost folosit in literatura de specialitate in cercetarea CA.
Strategia de control utilizeaza nivelul de eficacitate al actuatoarelor si redistribuie controlul catre actuatoarele ramase atunci cand se intampla o defectiune; aceasta fiind noutatea acestui capitol.
6.2 Proiectarea controlerului
Se considera
sistemul liniar invariant in timp de ordinul ![]() cu
cu ![]() intrari:
intrari:
![]() (6.1)
(6.1)
unde ![]() cu
cu ![]() B se poate scrie ca:
B se poate scrie ca:
![]() (6.2)
(6.2)
Intrarea controlului virtual se poate scrie ca:
![]() (6.3)
(6.3)
unde ![]() care reprezinta efortul de control total
produs de actuatoare.
care reprezinta efortul de control total
produs de actuatoare.
![]() (6.4)
(6.4)
![]() (6.5)
(6.5)
unde ![]() .
Solutia optima pentru (6.5) este
.
Solutia optima pentru (6.5) este
![]() (6.6)
(6.6)
Adesea in
literatura de specialitate ![]() din (6.5) si (6.6) este setat la
identificarea, care da metodei clasice Moore-Penrose, pseudo-inversa. O alta
abordare este alegerea lui
din (6.5) si (6.6) este setat la
identificarea, care da metodei clasice Moore-Penrose, pseudo-inversa. O alta
abordare este alegerea lui ![]() sa fie o matrice diagonala formata din limitele
patratice de suprafata. In acest fel
sa fie o matrice diagonala formata din limitele
patratice de suprafata. In acest fel ![]() scaleaza fiecare suprafata de control bazata
pe devierea limitei pentru a distrubui in mode gal efortul de control.
scaleaza fiecare suprafata de control bazata
pe devierea limitei pentru a distrubui in mode gal efortul de control.
6.2.1 Formularea problemei
In acest capitol se considera situatia in care se dezvolta un defect in sistemul (6.1) asociat cu actuatoarele. Se v-a presupune ca in caz de aparitie a defectelor actuatorului ecuatia (6.1) poate fi scrisa ca:
![]() (6.7)
(6.7)
unde ![]() unde
unde ![]() sunt scalari care satisfac conditia
sunt scalari care satisfac conditia ![]() .
Daca
.
Daca ![]() actuatorul merge perfect, daca
actuatorul merge perfect, daca ![]() o eroare este prezenta iar daca
o eroare este prezenta iar daca ![]() actuatorul a cedat complet.
actuatorul a cedat complet.
In acest
capitol se v-a considera matricea de greutate ![]() .
Daca informatiile despre defectele actuatorului sunt disponibile la un FDI
astfel incat valorile
.
Daca informatiile despre defectele actuatorului sunt disponibile la un FDI
astfel incat valorile ![]() ale
eficacitaii actuatorului sunt cunoscute semnalul de control de la 'controlul virtual'
ale
eficacitaii actuatorului sunt cunoscute semnalul de control de la 'controlul virtual' ![]() poate fi redistribuit la actuatoarele ramase
functionale folosind
poate fi redistribuit la actuatoarele ramase
functionale folosind ![]() in (6.6).
in (6.6). ![]() a fost aleasa ca:
a fost aleasa ca:
![]() (6.8)
(6.8)
Ca o
consecinta directa ![]() si
si ![]() .
.
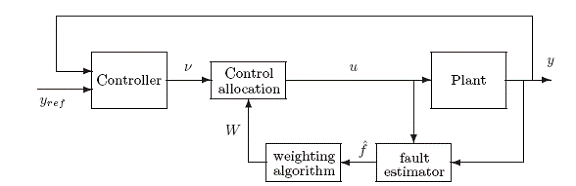
Fig. 6.1
Figura 6.1
ilustreaza strategia alocari de control a FTC. Alocarea de control v-a depinde
de eficacitatea actuatoarelor. Informatiile necesare pentru a calcula pe ![]() pot fi furnizate de un sistem de reconstructie a defectelo sau folosind
masuratorile devierii actuatorului comparate cu cererea care este disponibila
in multe sisteme. O alternativa sunt sistemele de reconstructie a defectelor
bazate pe filtre Kalman. Din (6.8) deducem daca un actuator se defecteaza, ponderea
pot fi furnizate de un sistem de reconstructie a defectelo sau folosind
masuratorile devierii actuatorului comparate cu cererea care este disponibila
in multe sisteme. O alternativa sunt sistemele de reconstructie a defectelor
bazate pe filtre Kalman. Din (6.8) deducem daca un actuator se defecteaza, ponderea ![]() v-a fi schimbata si intrarea de control
v-a fi schimbata si intrarea de control ![]() v-a fi realocata pentru a minimiza utilizarea
suprafetei de control defecta. In cazul defectarii totale a suprafetei de
control
v-a fi realocata pentru a minimiza utilizarea
suprafetei de control defecta. In cazul defectarii totale a suprafetei de
control ![]() ,
,
![]() si deci componenta
si deci componenta ![]() a lui
a lui ![]() devine mare. Prin urmare
devine mare. Prin urmare ![]() este complet redistribuit la alte actuatoare.
In multe sisteme cu redundanta a actuatoarelor ipoteza din capitolul (6.2) ca
este complet redistribuit la alte actuatoare.
In multe sisteme cu redundanta a actuatoarelor ipoteza din capitolul (6.2) ca ![]() nu este valabila si deci factorizarea perfecta
din (6.2) nu poate fi asigurata. Totusi
starile sistemului pot fi oricand rearanjate si matricea B din (6.2) poate fi
scrisa ca:
nu este valabila si deci factorizarea perfecta
din (6.2) nu poate fi asigurata. Totusi
starile sistemului pot fi oricand rearanjate si matricea B din (6.2) poate fi
scrisa ca:
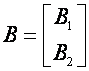 (6.9)
(6.9)
Separarea legii de control de sarcina alocarii de control are loc in mod natural cu metodele de proiectare ca liniarizarea feedback care foloseste controlul virtual intermediar.
In cele mai
multe sisteme de avionica obiectivele controlului pot fi obtinute prin
comandarea unor momente dezirabile pentru a fi generate de suprafata de
control. In sistemele de avionica de exemplu, canalele asociate cu ![]() sunt ecuatiile acceleratiei unghiulare in
ruliu,tangaj si giratie.Aici se presupune ca
sunt ecuatiile acceleratiei unghiulare in
ruliu,tangaj si giratie.Aici se presupune ca ![]() v-a reprezenta contribitia cea mai importanta
a actiunii de control a sistemului. Daca
v-a reprezenta contribitia cea mai importanta
a actiunii de control a sistemului. Daca ![]() ;
aceasta reprezinta o situatie extrema unde efectul total de control se face
numai prin
;
aceasta reprezinta o situatie extrema unde efectul total de control se face
numai prin ![]() .
.
Aici in
proiectarea controlerului si analiza stabilitatii se va considera ![]() .
Se v-a presupune ca starile sistemului (6.1) au fost transformate astfel incat
.
Se v-a presupune ca starile sistemului (6.1) au fost transformate astfel incat ![]() .
Aceasta este intotdeauna posibil deoarece
.
Aceasta este intotdeauna posibil deoarece ![]()
![]() (6.10)
(6.10)
![]() (6.11)
(6.11)
unde
![]() (6.12)
(6.12)
Expresia (6.7) devine :
![]()
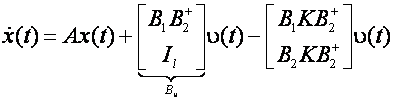 (6.13)
(6.13)
Obiectivul
este sa folosim tehnica SMC pentru a sintetiza controlul virtual ![]() .
.
![]() (6.14)
(6.14)
Daca o lege de control poate fi dezvoltata care sa forteze traiectoria buclei inchise pe suprafata S in timp finit si sa constranga starile sa ramana acolo, atunci se poate spune ca o miscare de alunecare ideala a fost obtinuta. Selectia suprafetei de alunecare este primul pas al oricarui proces de proiectare si defineste performantele sistemului in bucla inchisa.
Suprafata de
alunecare v-a fi proiectata bazandu-se pe conditia nominala de defecte nule ![]() .
Al doilea aspect al proiectarii controlului este sinteza legii de control asfel incat sa garanteze ca suprafata este
atinsa in timp finit si modul de alunecare este ulterior mentinut.
.
Al doilea aspect al proiectarii controlului este sinteza legii de control asfel incat sa garanteze ca suprafata este
atinsa in timp finit si modul de alunecare este ulterior mentinut.
Ecuatia (6.13) poate fi scrisa ca:
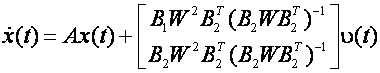 (6.15)
(6.15)
Daca
![]() (6.16)
(6.16)
ecuatia (6.15) poate fi scrisa ca
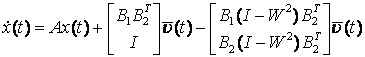 (6.17)
(6.17)
Daca ![]() atunci sistemul nominal este
atunci sistemul nominal este
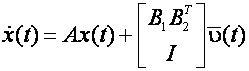 (6.18)
(6.18)
Daca
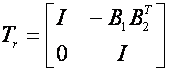 (6.19)
(6.19)
atunci ecuatia (6.17) devine
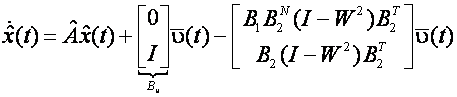 (6.20)
(6.20)
unde ![]() si
si
![]() (6.21)
(6.21)
Deoarece din
constructie matricea ![]() rezulta ca
rezulta ca
![]()
si de aici
![]() (6.22)
(6.22)
Ecuatia (6.20) devine
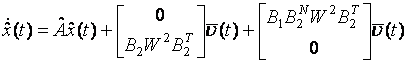 (6.23)
(6.23)
ultimul termen din (6.23) este zero. Definim
![]() (6.24)
(6.24)
si de aici (6.23) devine
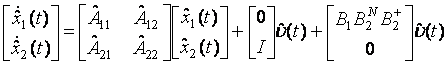 (6.25)
(6.25)
unde
![]() (6.26)
(6.26)
Propozitia 1 :
Exista
scalarul ![]() care este finit si independent de
care este finit si independent de ![]() astfel incat
astfel incat
![]() (6.27)
(6.27)
Demonstratie:
Deoarece ![]() rezulta dupa cum urmeaza:
rezulta dupa cum urmeaza:
Observatia 1: daca W nu este diagonala, ![]() nu mai
este nevoie sa fie limitat. Legea de control virtuala v-a fi acum proiectata
bazandu-se pe sistemul nominal fara defecte in care partitia de sus a
termenului din (6.25) este zero. In coordonatele
nu mai
este nevoie sa fie limitat. Legea de control virtuala v-a fi acum proiectata
bazandu-se pe sistemul nominal fara defecte in care partitia de sus a
termenului din (6.25) este zero. In coordonatele ![]() din (6.25) o alegere convenabila pentru
suprafata de alunecare este:
din (6.25) o alegere convenabila pentru
suprafata de alunecare este:
![]() (6.28)
(6.28)
unde ![]()
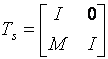 (6.29)
(6.29)
Ecuatia (6.25) devine
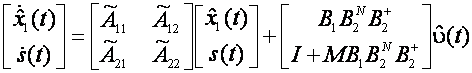 (6.30)
(6.30)
unde ![]() este definit in (6.26).
este definit in (6.26).
![]() (6.31)
(6.31)
unde ![]() este definit in (6.21). Definim
este definit in (6.21). Definim
![]() (6.32)
(6.32)
De aici
rezulta ca ![]() .
Deoarece
.
Deoarece ![]() este independent de
este independent de ![]() ,
,
![]() poate fi calculat folosind teorema 2. Daca
poate fi calculat folosind teorema 2. Daca ![]() este controlabila, atunci
este controlabila, atunci ![]() este
controlabila si
este
controlabila si ![]() poate fi ales astfel incat
poate fi ales astfel incat ![]() sa fie stabila. Matricea
sa fie stabila. Matricea ![]() poate fi aleasa si astfel incat
poate fi aleasa si astfel incat ![]() din (6.32) sa satisfaca
din (6.32) sa satisfaca ![]() .
.
Substituind (6.31) in partitia de sus in (6.30) rezulta miscarea de alunecare
![]() (6.33)
(6.33)
Observatia 2: in conditiile in care W=I rezulta
![]()
Si sitemul
in (6.33) cedeaza ![]()
![]() care este sistemul nominal de ordin redus al
miscarii de alunecare pentru care
care este sistemul nominal de ordin redus al
miscarii de alunecare pentru care ![]() a fost proiectat sa garanteze stabilitatea.
Sistemul in (6.33) depinde de
a fost proiectat sa garanteze stabilitatea.
Sistemul in (6.33) depinde de ![]() si deci stabilitatea trebuie sa fie stabilita.
Analiza stabilitatii examineaza ce se va intampla cu sistemul de ordin redus al
miscarii de alunecare atunci cand e supus la defecte. Ideea este sa folosim
instrumentele de proiectare pe care le avem la dispozitie pentru proiectarea
suprafetei de alunecare fara defecte.
si deci stabilitatea trebuie sa fie stabilita.
Analiza stabilitatii examineaza ce se va intampla cu sistemul de ordin redus al
miscarii de alunecare atunci cand e supus la defecte. Ideea este sa folosim
instrumentele de proiectare pe care le avem la dispozitie pentru proiectarea
suprafetei de alunecare fara defecte.
6.2.2 Analiza stabilitatii
Stabilitatea
modului de alunecare este dependenta de sistemul de ordin redus (6.33). In mod
obisnuit in SMC stabilitatea sistemului depinde doar de ![]() care este garantata sa fie stabila prin
alegerea lui
care este garantata sa fie stabila prin
alegerea lui ![]() .
.
![]() poate fi proiectat folosind metode de
proiectare a hiperplanului de alunecare standard presupunand o conditie
nominala fara defecte
poate fi proiectat folosind metode de
proiectare a hiperplanului de alunecare standard presupunand o conditie
nominala fara defecte ![]() .
Definim:
.
Definim:
![]() (6.34)
(6.34)
unde ![]() reprezinta variabila Laplace. Presupunem ca
reprezinta variabila Laplace. Presupunem ca
![]() (6.35)
(6.35)
Propozitia 3
In timpul
unei erori sau defect pentru orice combinatie ![]() sistemul buclei inchise va fi stabil daca
sistemul buclei inchise va fi stabil daca
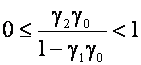 (6.36)
(6.36)
Demonstratie
Consideram sistemul de ordin redus din ecuatia (6.33) rescrisa ca
![]() (6.37)
(6.37)
![]() (6.38)
(6.38)
unde
![]() (6.39)
(6.39)
Folosind faptul ca in general ![]() atunci
atunci
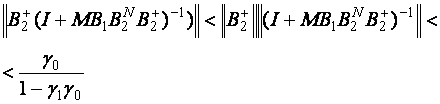
Daca
![]() (6.41)
(6.41)
Atunci (6.33) este stabila
Observatie: Atat ![]() depind
de proietarea suprafetei de alunecare deoarece ele depind de
depind
de proietarea suprafetei de alunecare deoarece ele depind de ![]() si sunt independente de
si sunt independente de ![]() .
Scalarul
.
Scalarul ![]() depinde de
depinde de ![]() dar este independent de
dar este independent de ![]() .
.
Observatie :
Daca ![]() atunci
atunci ![]() ,
chiar mai mult
,
chiar mai mult 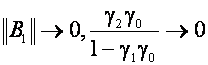 .
.
Acest lucru inseamna pe larg pentru sistemele slab cuplate in care ![]() este mic,ca abordarea va fi fezabila. In
situatia in care
este mic,ca abordarea va fi fezabila. In
situatia in care ![]() poate fi considerata o situatie speciala caz
in care
poate fi considerata o situatie speciala caz
in care ![]() . Ecuatia (6.36) reprezinta un
test pentru a garanta stabilitatea in bucla inchisa a sistemului atunci cand
apar defecte. O caracteristica
importanta este aceea ca in scopul ca (6.33) sa aiba norma pseudo-inversei
. Ecuatia (6.36) reprezinta un
test pentru a garanta stabilitatea in bucla inchisa a sistemului atunci cand
apar defecte. O caracteristica
importanta este aceea ca in scopul ca (6.33) sa aiba norma pseudo-inversei ![]() care
depinde de
care
depinde de ![]() trebuie sa fie delimitata
trebuie sa fie delimitata ![]() .
.
6.2.3 Legile de control ale modului de alunecare
In continuare se prezinta proiectarea unui controler bazat pe sistemul (6.30). legea de control propusa are o structura data de
![]() unde:
unde:
![]() (6.42)
(6.42)
si componenta neliniara este definita ca
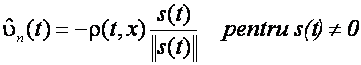 (6.43)
(6.43)
unde ![]()
Propozitia 4 : Presupunem ca matricea hiperplanului ![]() a fost aleasa ca
a fost aleasa ca ![]() sa fie stabila si alegem
sa fie stabila si alegem
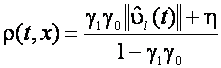 (6.44)
(6.44)
Aceasta asigura ca o miscare de alunecare are loc in ![]() in timp finit.
in timp finit.
Demonstratie
Din (6.30) rezulta
![]()
![]()
si
![]()
![]() (6.45)
(6.45)
Aceasta implica
![]() (6.46)
(6.46)
Observatie.
Se poate arata ca ![]() definit in (6.42) pote fi scris ca
definit in (6.42) pote fi scris ca ![]() .
. ![]() poate fi definit ca:
poate fi definit ca:
![]() (6.47)
(6.47)
Retinem ca
in cea mai mare parte a literaturii de specialitate SMC a fost testat cu succes
pe sisteme cu defecte ale actuatoarelor. Cu conditia ca ![]() satisface ecuatia (6.36) controlerul modului
de alunecare pentru ssitemul virtual propus mai sus, poate face fata defectarii
totale a actuatorului in sistemul initial cu conditia ca
satisface ecuatia (6.36) controlerul modului
de alunecare pentru ssitemul virtual propus mai sus, poate face fata defectarii
totale a actuatorului in sistemul initial cu conditia ca ![]() .
.
Observatie.
In acest capitol efectul de pozitie asupra actuatoarelor nu se ia in
considerare. Oricum daca o viteza limita sau pozitie limitata este depasita
aceasta ar putea fi interpretata de mecanismul de estimare ca defect, deoarece
pozitia actuala a actuatorului ar fi diferita decat cea asteptata. Sistemul
propus va incerca atunci sa reduca sarcina in acest canal si sa redistribuie
efortul de control catre celelalte actuatoare care ar diminua efectul de
saturatie. Pana
acum s-a presupus ca eficacitatea ![]() care il determina pe
care il determina pe ![]() si
si ![]() sunt cunoscute. In realitate intotdeauna v-a
exista o eroare in calcularea lui
sunt cunoscute. In realitate intotdeauna v-a
exista o eroare in calcularea lui ![]()
Efectul recontructiei imperfecte a defectului
Se considera ecuatia (6.7). Definim
![]() (6.48)
(6.48)
Presupunem
![]() (6.49)
(6.49)
unde ![]()
![]() .
Deoarece (I-K)=W din (6.7) rezulta
.
Deoarece (I-K)=W din (6.7) rezulta
![]() (6.50)
(6.50)
![]() (6.51)
(6.51)
Atunci (6.50) devine
![]() (6.52)
(6.52)
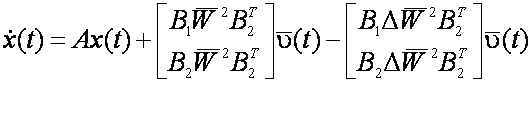
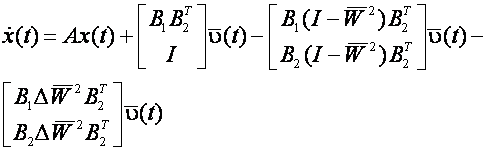
Comparativ cu (6.17) ecuatia (6.53) are un termen aditional dependent de erorile si defectele in reconstructie. Ecuatia (6.53) devine
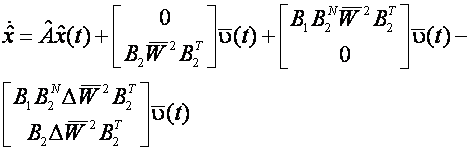
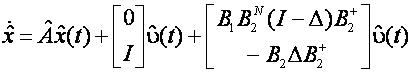 (6.55)
(6.55)
Consideram o alta transformare de coordonate ![]() definita in (6.29), atunci (6.55) devine
definita in (6.29), atunci (6.55) devine
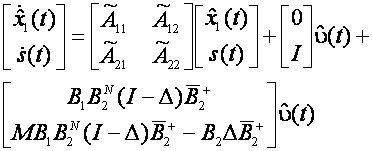 (6.56)
(6.56)
![]() (6.57)
(6.57)
Substituind in prima ecuatie (6.56), aceasta da urmatorul sistem de ordin redus
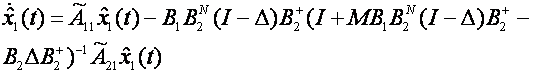
Propozitia 5. Presupunem ca ecuatia (6.36) este valabila. In
timpul unei erori sau unui defect pentru orice combinatie ![]() sistemul buclei inchise v-a fi stabil daca
nepotrivirea dintre eroarea actuala sau reconstruita satisface
sistemul buclei inchise v-a fi stabil daca
nepotrivirea dintre eroarea actuala sau reconstruita satisface
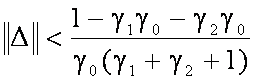 (6.59)
(6.59)
Demonstratie. Consideram sistemul de ordin redus din ecuatia (6.58) care poate fi rescris ca
![]() (6.60)
(6.60)
Inegalitatea (6.59) implica
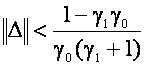 (6.61)
(6.61)
Deoarece
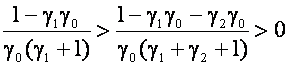
Deoarece
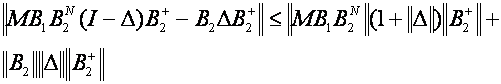
Inegalitatea (6.61) implica
![]() (6.62)
(6.62)
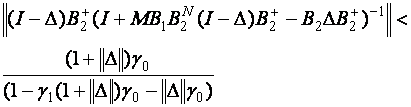 (6.63)
(6.63)
Daca este valabila urmatoarea inegalitate
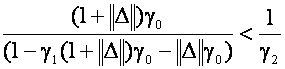 (6.64)
(6.64)
atunci (6.58) este stabila. Daca (6.64) si (6.59) sunt valabile atunci demonstratia este completa.
Propozitia 6. Presupunem ca matricea hiperplanului M a fost aleasa
astfeel incat ![]() sa fie stabila si
sa fie stabila si
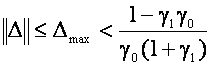 (6.65)
(6.65)
Apoi alegand
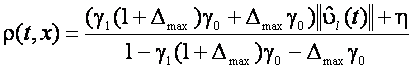 (6.66)
(6.66)
se asigura ca o miscare de alunecare are loc pe S in timp finit.
Demonstratie. Din (6.56) rezulta
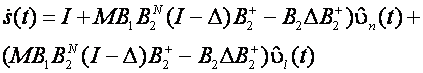
Dupa ce substituim ![]() din (6.42). in consecinta subtituind
din (6.42). in consecinta subtituind ![]() in (6.43) rezulta
in (6.43) rezulta
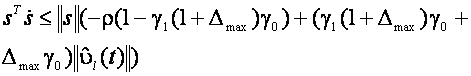 (6.67)
(6.67)
Aceasta implica
![]() (6.68)
(6.68)
Probleme de proiectare ale modului de alunecare
Pe baza analizei de mai sus a stabilitatii, problemele proiectarii modului de alunecare pot fi rezumate dupa cum urmeaza:
1) Calcule de preproiectare
a) Se face o reordonare a starilor in (6.7)
astfel incat intrarile matricei de
distributie ![]() sunt impartite pentru a identifica pe
sunt impartite pentru a identifica pe ![]() .
.
b) Se scaleaza starea astfel
incat ![]()
c) Se schimba coordonatele
folosind transformarea liniara ![]() ,
unde
,
unde ![]() este data in ecuatia (6.19) pentru a obtine
forma canonica in (6.25).
este data in ecuatia (6.19) pentru a obtine
forma canonica in (6.25).
d) se calculeaza cel mai mic scalar posibil ![]() .
.
Aceasta valoare este un calcul si este independent de alegerea suprefetei de alunecare si a legii de control.
Proiectarea
matricii ![]()
Scopul proiectarii
este sa calculam pe ![]() din (6.28) astfel incat
din (6.28) astfel incat ![]() sa fie stabila. Aceasta este posibil daca
sa fie stabila. Aceasta este posibil daca ![]() )
este controlabila.
)
este controlabila.
Analiza stabilitatii
a)
Se
calculeaza si se verifica daca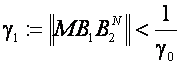 .
Daca nu se reproiecteaza
.
Daca nu se reproiecteaza ![]() .
.
b)
Se
calculeaza ![]() .
.
c)
Se
calculeaza ![]() .
Aceasta este toleranta mxima de neconcordanta dintre defectul actual si cel
estimat care garanteaza ca sistemul in bucla inchisa este stabil.
.
Aceasta este toleranta mxima de neconcordanta dintre defectul actual si cel
estimat care garanteaza ca sistemul in bucla inchisa este stabil.
Obtinerea legii de control virtuale se face folosind (6.42) si (6.43) si legea de control actuala folosind (6.47)
Simularea folosind programul ADMIRE
Concluzii
In acest capitol au fost prezentate sisteme pentru alocarea de control online a modului de alunecare pentru controlul tolerant la defecte. Nivelul de eficacitate al actuatoarelor este folosit de sistemul CA pentru a redistribui semnalele de control la actuatoarele ramase functionale atunci cand apar defecte. Acest capitol a oferit o analiza a sistemului de alocare de control a modului de alunecare propuse si a determinat gainul neliniar necesar pentru a mentine alunecarea.
Capitolul 7
Implementarea rezultatelor folosind simulatorul SIMONA
7.1 Introducere
Combinatia dintre modurile de alunecare si alocarea de control dezvoltate in ultimul capitol asigura un instrument puternic pentru dezvoltarea controlerelor cu toleranta la erori simple si robuste care lucreaza pentru o gama larga de erori/defecte fara sa necesite reconfigurarea.
Sistemele de alocare de control ale modului de alunecare au fost proiectate si testate pe un simulator cu 6 grade de libertate SIMONA de inalta fidelitate si neliniar bazat pe modelul FTLAB-747.
7.2Facilitati de testare cu simulatorul SIMONA
Testarea unui controler tolerant la erori/defecte este un proces important in determinarea eficientei sale in timpul defectelor. De obicei un controler nou proiectat este mai intai testat pe un model de referinta si apoi este testat pe un simulator de zbor inainte de a primi aprobarea sa fie testat intr-un zbor real. Pentru studiul erorilor si defectelor un model de avion de inalta fidelitate si neliniar poate simula indeaproape conditiile reale si performantele unui avion cu foarte mare acuratete. Simulatoarelele de zbor sunt deasemenea folosite inainte de zborul real pentru a obtine un feedback de la piloti despre eficacitatea controlerelor din sistem.
7.2.1 Simulatorul Simona
Simulatorul ofera cercetatorilor un instrument puternic care poate fi adaptat diverselor utilizari. A fost folosit pentru testarea sistemelor fly-by-wire, algoritmilor de control si de zbor si a controlului traficului aerian. O retea modulara de calculatoare personale ofera puterea de procesare pentru simulator. O retea de fibra optica de inalta viteza asigura sincronizarea si comunicarea tuturor computerelor.
7.3 Proiectarea controlerului
Cele 12
stari ale corpului rigid ale avionului B-747 pot fi imartite in 6 stari axiale
longitudinale si 6 stari laterale si directionale care sunt toate determinate
din cele 6 grade de libertate ale ecuatiei de miscare. Starile sunt date de ![]() .
Pentru axa longitudinala starile sunt viteza de tangaj
.
Pentru axa longitudinala starile sunt viteza de tangaj ![]() ,
viteza adevarata a aerului '
,
viteza adevarata a aerului '![]() ',
unghiul de atac
',
unghiul de atac ![]() ,
unghiul de tangaj '
,
unghiul de tangaj '![]() '
si altitudinea '
'
si altitudinea '![]() '.
Pentru axa laterala si directionala starile sunt viteza de ruliu
'.
Pentru axa laterala si directionala starile sunt viteza de ruliu ![]() ,viteza
de giratie
,viteza
de giratie ![]() ,unghiul de derapaj '
,unghiul de derapaj '![]() ',
unghiul de ruliu '
',
unghiul de ruliu '![]() '
si unghiul de giratie '
'
si unghiul de giratie '![]() '.
Suprafetele de control cuprind 4 eleroane, 12 spoilere, 2 profundoare, un
stabilizator orizontal si 4 motoare.
'.
Suprafetele de control cuprind 4 eleroane, 12 spoilere, 2 profundoare, un
stabilizator orizontal si 4 motoare.
In acest
capitol se ia in considerare atat controlul lateral cat si cel longitudinal.
Unul dintre obiectivele proiectarii controlerului este aducerea unui avion cu
defecte in apropierea conditiilor de aterizare. Acest lucru poate fi obtinut
prin urmarirea adecvata a comenzilor
unghiului de ruliu ![]() si a unghiului de derapaj
si a unghiului de derapaj ![]() folosind controlerul lateral a unghiului de zbor si viteza adecvata a
aerului folosind controlerul longitudinal. In urma liniarizarii rezulta un sistem liniar de ordinul 12 asociat cu
starile laterale si longitudinale. Pentru proiectare nu se retin decat primele
4 stari longitudinale si laterale.
folosind controlerul lateral a unghiului de zbor si viteza adecvata a
aerului folosind controlerul longitudinal. In urma liniarizarii rezulta un sistem liniar de ordinul 12 asociat cu
starile laterale si longitudinale. Pentru proiectare nu se retin decat primele
4 stari longitudinale si laterale.
Pentru sistemul generat (6.7), daca ![]() reprezinta starea de integrare rezulta
reprezinta starea de integrare rezulta
![]() (7.5)
(7.5)
unde ![]() este
matricea distributiilor asociata cu iesirile controlerului si semnalul diferentiabil
este
matricea distributiilor asociata cu iesirile controlerului si semnalul diferentiabil ![]() satisface conditia :
satisface conditia :
![]() (7.6)
(7.6)
Cu ![]() o matrice stabila din proiectare si
o matrice stabila din proiectare si ![]() este un vector constant. Definind
este un vector constant. Definind ![]() rezulta
rezulta
![]() (7.7)
(7.7)
unde
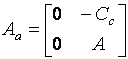
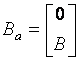
 (7.8)
(7.8)
Daca ![]() este controlabila si
este controlabila si ![]() nu are nici un zero in origine atunci
nu are nici un zero in origine atunci ![]() este controlabila. Se defineste functia de
comutatie
este controlabila. Se defineste functia de
comutatie
![]() (7.9)
(7.9)
unde ![]() .
.
Unde ![]() .
Legea de control virtual are doua componente una liniara si cealalta neliniara.
.
Legea de control virtual are doua componente una liniara si cealalta neliniara.
![]() unde
unde ![]() si
si ![]()
Componenta neliniara este
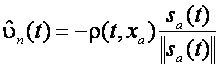 pentru
pentru
![]() (7.10)
(7.10)
Din (6.47) rezulta
![]() (7.11)
(7.11)
7.3.1 Proiectarea controlerului lateral
Capitolul 8
Modelul de referinta al modului de alunecare FTC
8.1 introducere
Asa numitul model cadru de referinta este unul dintre multele moduri de a obtine reconfigurarea sau adaptarea controlerului. Popularitatea modelului cadru de referinta pentru adaptare si FTC se datoreaza mai multor caracteristici avantajoase. Multe performante sunt date in domeniul timp de exemplu timpul de crestere, raportul de amortizare etc. acestea pot fi reprezentate ca o functie ideala de transfer care devine semnalul de referinta pe care sistemul in bucla inchisa trebuie sa il urmeze. Alt avantaj al folosirii modelului cadru de referinta pentru FTC este acela cap ermite modelului de referinta sa fie schimbat online pentru a face fata schimbarilor conditiilor de operare in special la aparitia erorilor sau defectelor. Acest capitol analizeaza folosirea modelului cadru de referinta combinat cu SMC si CA. un avantaj al acestei abordari este absenta integratoarelor; acest lucru elimina pericolul in fata saturatiei si depasirea ratelor limita. Introducerea gainului adaptiv in controlerul SMC elimina nevoia de gainuri mari si nenecesare in controlul liniar.
8.2 Proiectarea controlerului
Se va presupune ca sistemul asociat cu defectarea actuatorului poate fi scris ca
![]() (8.1)
(8.1)
unde![]() si
si ![]() satisface conditia
satisface conditia ![]() .
.
Acest model scalar arata descresterea eficacitatii unui actuator particular.
In cele mai multe strategii ale CA, semnalul de control este distribuit in mod
egal la toate actuatoarele sau distribuit in functie de limitele actuatorului.
Se vor lua in considerare doua strategii diferite de CA. Prima, informatia
despre ![]() va fi incorporata in algoritmul de alocare
prin intermediul matricii de pondere
va fi incorporata in algoritmul de alocare
prin intermediul matricii de pondere ![]() ,
astfel incat controlul este redistribuit catre actuatoarele ramase atunci cand
unele se defecteaza. Ideea este
ca daca un actuator se defecteaza semnalul de intrare
,
astfel incat controlul este redistribuit catre actuatoarele ramase atunci cand
unele se defecteaza. Ideea este
ca daca un actuator se defecteaza semnalul de intrare ![]() este
realocat pentru a minimiza folosirea suprafetei de control defecte. A doua
strategie se bazeaza pe o abordare pe scara larga a CA ; distributia fixa
si egala a semnalelor de control. Acest lucru este motivat de faptul ca
informatia despre
este
realocat pentru a minimiza folosirea suprafetei de control defecte. A doua
strategie se bazeaza pe o abordare pe scara larga a CA ; distributia fixa
si egala a semnalelor de control. Acest lucru este motivat de faptul ca
informatia despre ![]() in (8.1) nu este intotdeauna disponibila. Aici
CA este setat sa fie fix si semnalele de
control sunt distribuite in mod egal la toate actuatoarele si deci independent
de informatia eronata. Presupunem ca starile sistemului pot fi reordonate si
(8.1) poate fi scris ca
in (8.1) nu este intotdeauna disponibila. Aici
CA este setat sa fie fix si semnalele de
control sunt distribuite in mod egal la toate actuatoarele si deci independent
de informatia eronata. Presupunem ca starile sistemului pot fi reordonate si
(8.1) poate fi scris ca
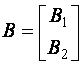 (8.2)
(8.2)
Presupunem
ca starile sistemului in ecuatia (8.1) au fost transformate astfel incat ![]() si
si ![]() .
Rezulta
.
Rezulta
![]() (8.3)
(8.3)
si de aici
![]() (8.4)
(8.4)
unde pseudo-inversa este aleasa ca
![]()
![]() (8.5)
(8.5)
Alocarea de control online
Ideea este sa
obtinem infrmatia despre ![]() si
incorporarea lui in algoritmul de alocare prin intermediul matricei de pondere
si
incorporarea lui in algoritmul de alocare prin intermediul matricei de pondere ![]() .
Deci controlul este redistribuit catre actuatoarele ramase functionale pentru a
minimiza folosirea suprafetei de control defecte. Ecuatia (8.1) poate fi scrisa
ca
.
Deci controlul este redistribuit catre actuatoarele ramase functionale pentru a
minimiza folosirea suprafetei de control defecte. Ecuatia (8.1) poate fi scrisa
ca
![]() (8.6)
(8.6)
Definim
![]()
![]() (8.7)
(8.7)
Ecuatia (8.6) poate fi scrisa ca
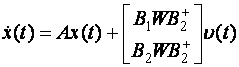 (8.8)
(8.8)
Greutatea ![]() se va alege
se va alege
![]() (8.9)
(8.9)
Ecuatia (8.8) poate fi scrisa ca
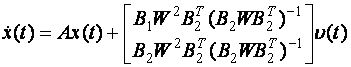 (8.10)
(8.10)
Daca un control virtual este selectat ca
![]() (8.11)
(8.11)
atunci ecuatia (8.10) poate fi scrisa ca
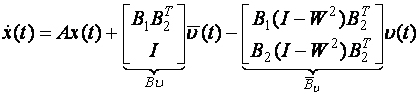 (8.12)
(8.12)
Daca nu
exista defecte ![]() .
.
Consideram
![]() (8.13)
(8.13)
unde ![]() este un semnal de referinta. Definim
este un semnal de referinta. Definim
![]() (8.14)
(8.14)
Din (8.12) si (8.13) rezulta eroarea sistemului
![]() (8.15)
(8.15)
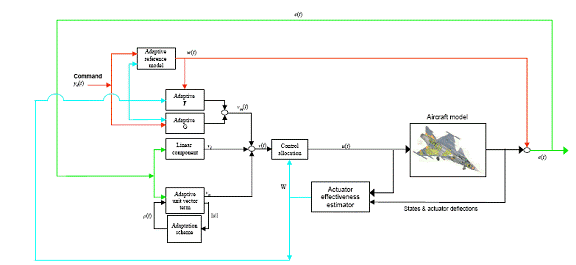
Fig 8.1
Presupunem
ca matricele ![]() sunt date de
sunt date de
![]() (8.16)
(8.16)
si
![]() (8.17)
(8.17)
Tehnica SMC
va fi folosita pentru a sintetiza pe ![]() .
Definim functia de comutare ca fiind:
.
Definim functia de comutare ca fiind:
![]() (8.18)
(8.18)
![]() este hiperplanul definit ca
este hiperplanul definit ca
![]()
Suprafata de
alunecare este proiectata bazata pe conditia nominala fara erori ![]() .
Folisind ecuatia (8.16) ecuatia (8.15) se poate rescrie ca
.
Folisind ecuatia (8.16) ecuatia (8.15) se poate rescrie ca
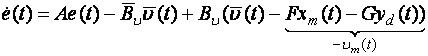 (8.19)
(8.19)
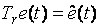
Daca
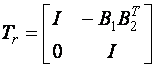 (8.20)
(8.20)
atunci ecuatia (8.19) devine
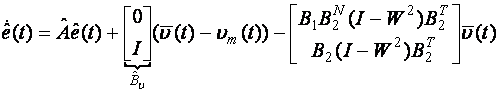
unde ![]() si
si
![]() (8.22)
(8.22)
Din
constructie ![]() si
si
![]() (8.23)
(8.23)
Definim o alta scalare a controlului virtual
![]() (8.24)
(8.24)
Ecuatia (8.21) devine
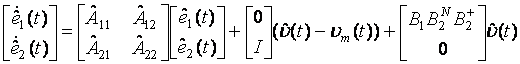
unde
![]() (8.26)
(8.26)
Asa cum s-a
aratat in capitolul 6 la propozitia 2 exista un scalar ![]() finit si independent de
finit si independent de ![]() .
.
![]() (8.27)
(8.27)
In coordonate ![]() o alegere potrivita a matricei
suprafetei de alunecare este
o alegere potrivita a matricei
suprafetei de alunecare este
![]() (8.28)
(8.28)
unde M reprezinta gradul de
libertate. Se introduce o noua transformare ![]()
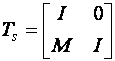 (8.29)
(8.29)
Ecuatia (8.25) devine
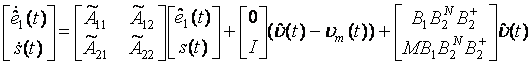
unde
![]() (8.31)
(8.31)
si
![]() (8.32)
(8.32)
Daca o lege de control este proiectata pentru a induce o miscare de
alunecare, in timpul alunecarii controlul echivalent necesar pentru a mentine
alunecarea se obtine rezolvand ![]() din ecuatia (8.30)
din ecuatia (8.30)
![]() (8.33)
(8.33)
Matricea ![]() a
suprafetei de alunecare a fost aleasa astfel incat
a
suprafetei de alunecare a fost aleasa astfel incat ![]() sa fie stabila si
sa fie stabila si ![]() pentru
pentru ![]()
Din (8.33) si (8.30) rezulta
 (8.34)
(8.34)
Analiza stabilitatii
Stabilitatea
modului de alunecare este dependenta de sistemul de ordin redus. Deoarece din
constructie modelul de referinta este stabil, pentru un semnal limitat ![]() ,
semnalul
,
semnalul ![]() este delimitat si mareste pe
este delimitat si mareste pe ![]() .
De aici stabilitatea sistemului de ordin redus conduce miscarea de alunecare
care depinde de
.
De aici stabilitatea sistemului de ordin redus conduce miscarea de alunecare
care depinde de
![]() (8.35)
(8.35)
Definim
![]() (8.36)
(8.36)
Definim urmatorii scalari
![]() (8.37)
(8.37)
![]()
![]() (8.38)
(8.38)
Sistemul buclei inchise va fi stabil daca
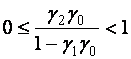 (8.39)
(8.39)
Unde ![]() este un scalar pozitiv definit ca in (8.27).
este un scalar pozitiv definit ca in (8.27).
O lege de control a modului de alunecare
In
continuare v-a fi proiectat un controler pentru modul de alunecare bazat pe
sistemul (8.30) care respecta controlul virtual ![]() .
Legea de control propusa este data de
.
Legea de control propusa este data de ![]()
unde
![]() (8.40)
(8.40)
Componenta neliniara este definita ca
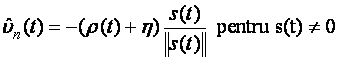 (8.41)
(8.41)
![]() este
definit ca
este
definit ca
![]() (8.42)
(8.42)
In cea mai
mare parte a literaturii de specialitate desi SMC a fost testat cu succes pe
sisteme cu actuatoare defecte s-a sustinut ca SMC nu poate face fata direct
defectarii totale a actuatorului. Intr-o situatie fara defecte nu este necesar
si nu este recomandat sa avem un gain mare pe termenul de comutatie, desi in
mod ideal termenul ![]() ar trebui numai sa se adapteze la debutul unui
defect si sa reactioneze in consecinta. Se poate observa cu usurinta din (8.40)
ca daca
ar trebui numai sa se adapteze la debutul unui
defect si sa reactioneze in consecinta. Se poate observa cu usurinta din (8.40)
ca daca ![]() este limitat,
este limitat, ![]() este limitat si el de
este limitat si el de
![]() (8.43)
(8.43)
unde ![]() sunt constante pozitive. Gainul din ecuatia
(8.41) este definit ca
sunt constante pozitive. Gainul din ecuatia
(8.41) este definit ca
![]() (8.44)
(8.44)
Scalarul ![]() este
este
![]() (8.45)
(8.45)
unde
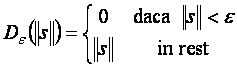 (8.46)
(8.46)
Aici ![]() este setat sa fie mic si ajuta la definirea
stratului limita de pe suprafata
este setat sa fie mic si ajuta la definirea
stratului limita de pe suprafata ![]() ,
in interiorul caruia cu o aproximare mica are loc o alunecare ideala. Daca
apare un defect care face miscarea de alunecare sa scada astfel incat starile sa evolueze in afara
stratului limita
,
in interiorul caruia cu o aproximare mica are loc o alunecare ideala. Daca
apare un defect care face miscarea de alunecare sa scada astfel incat starile sa evolueze in afara
stratului limita ![]() ,
atunci coeficientii dinamici
,
atunci coeficientii dinamici ![]() cresc in valoare pentru a forta starile inapoi
in interiorul stratului limita din jurul suprafetei de alunecare.
cresc in valoare pentru a forta starile inapoi
in interiorul stratului limita din jurul suprafetei de alunecare.
Alocarea fixa de control
Aici CA va
fi fix iar ![]() va fi utilizat in ecuatia (8.5) in loc de
va fi utilizat in ecuatia (8.5) in loc de
![]() .
Aici vom avea
.
Aici vom avea
![]() (8.62)
(8.62)
Ecuatia (8.4) devine
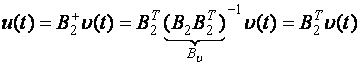 (8.63)
(8.63)
Ecuatia (8.1) se poate scrie ca
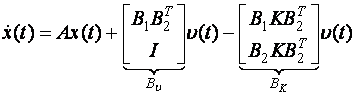 (8.64)
(8.64)
Eroarea sistemului este
![]() (8.65)
(8.65)
Definim
![]() (8.66)
(8.66)
Atunci ecuatia (8.65) se poate rescrie ca
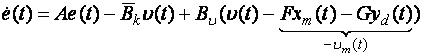 (8.67)
(8.67)
Se introduce
transformarea de coordonate ![]() .
.
![]() este defit ca
este defit ca 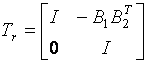 . Daca
. Daca ![]() atunci
ecuatia (8.67) devine
atunci
ecuatia (8.67) devine
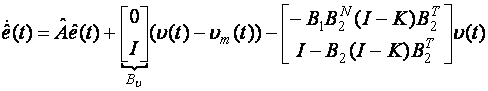 (8.68)
(8.68)
Definim
![]() (8.69)
(8.69)
![]() (8.70)
(8.70)
Se face
schimbarea de coordonate ![]() . Unde
. Unde ![]() este definit ca in (8.29).Ecuatia (8.68) devine
este definit ca in (8.29).Ecuatia (8.68) devine

![]() se alege astfel incat
se alege astfel incat ![]() sa fie stabila.
sa fie stabila.
Legea de control echivalenta necesara pentru a mentine alunecarea este obtinuta din partitia de jos a ecuatiei (8.71)
![]()
 (8.73)
(8.73)
Sistemul in bucla inchisa descris in ecuatia (8.73) va fi stabil daca ecuatia (8.39) este satisfacuta.
8.5 Concluzii
In acest capitol au fost propuse doua strategii folosind metoda CA. O strategie se bazeaza pe redistribuirea controlului online iar cealalta foloseste siteme de distribuire a semnalelor in mod egal. Au fost de asemenea propuse un gain adaptiv neliniar si un model de referinta adaptiv pentru sistemul FTC, in prima strategie CA nivelul de eficacitate al actuatoarelor este folosit pentru a redistribui semnalele de control catre actuatoarele ramase finctionale cand apare un defect. A doua strategie CA se bazeaza pe distribuirea semnalelor in mod egal chiar daca sistemul este defect. Gainul adaptiv neliniar si modelul de referinta asigura asigura
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4791
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved