| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Pentru sistemele policomponente deschise si cele inchise cu reactii chimice, potentialele termodinamice F si G depind si de compozitie, pe langa parametrii de stare p, V, T.
Diferentiala totala a potentialului termodinamic G (mai des folosit decat potentialul F) este:
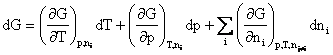 (4.189)
(4.189)
in care:
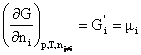 (4.190)
(4.190)
![]() este entalpia libera molara partiala in conditii izoterm-izobare si la
compozitie constanta si se numeste potential chimic cu notatia i data de Gibbs.
este entalpia libera molara partiala in conditii izoterm-izobare si la
compozitie constanta si se numeste potential chimic cu notatia i data de Gibbs.
Conform relatiei (4.190), potentialul chimic reprezinta variatia entalpiei libere a sistemului la adaugarea unui mol de substanta la presiune, temperatura si compozitie chimica constanta.
Inlocuind expresiile derivatelor partiale (4.168) si (4.169), relatia (4.189) devine:
![]() (4.191)
(4.191)
Relatia (4.191) reprezinta una din expresiile generale ale ecuatiei fundamentale a termodinamicii chimice pentru sisteme deschise.
In conditii izoterm-izobare, din relatia (4.189) rezulta:
![]() (4.192)
(4.192)
si pentru un sistem:
![]() (4.193)
(4.193)
Derivand relatia (4.193) se obtine:
![]() (4.194)
(4.194)
si identificand cu ecuatia (4.192) rezulta:
![]() (4.195)
(4.195)
Relatia (4.195) se numeste ecuatia Gibbs-Duhem
pentru potential chimic care prin impartire cu ![]() devine:
devine:
![]() (4.196)
(4.196)
unde: xi = fractia molara a componentului i.
Derivatele partiale ale potentialului chimic se obtin aplicand proprietatile matematice ale functiilor de stare:
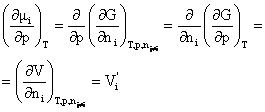 (4.197)
(4.197)
si
 (4.198)
(4.198)
unde: ![]() = volumul molar partial;
= volumul molar partial;
![]() = entropia molara partiala.
= entropia molara partiala.
Potentialul chimic depinde de compozitie care se poate exprima prin presiunile partiale ale componentilor gazosi, prin fractii molare sau concentratii molare.
Pentru un amestec de gaze perfecte in care componentul i are presiunea partiala pi, relatia (4.197) se poate scrie:
dμi = ![]() dp (4.199)
dp (4.199)
La gazele perfecte ![]() se
identifica cu volumul molar propriu Vi.
se
identifica cu volumul molar propriu Vi.
Daca se integreaza relatia
(4.199) intre presiunea normala ![]() si pi,
rezulta:
si pi,
rezulta:
![]() (4.200)
(4.200)
unde: ![]() = potentialul chimic standard al componentului i;
= potentialul chimic standard al componentului i;
![]() = 1 atm.
= 1 atm.
Inlocuind ![]() = RT/pi din ecuatia de
stare (2.17), relatia (4.200) devine:
= RT/pi din ecuatia de
stare (2.17), relatia (4.200) devine:
![]() (4.201)
(4.201)
Relatia (4.201) defineste potentialul chimic al unui gaz perfect.
Pe baza relatiei (2.33) ce defineste presiunea partiala in functie de fractia molara, relatia (4.201) se poate scrie:
![]() (4.202)
(4.202)
Expresia (4.202) valabila pentru amestecuri de gaze perfecte poate fi generalizata pentru toate amestecurile indiferent de starea lor de agregare, cu conditia sa se comporte ca amestecuri ideale (fara interactii).
Pentru amestecurile reale se introduce un factor de corectie cu care se inmulteste fractia molara:
ai = φixi (4.203)
unde: ai = activitate rationala (termodinamica);
i = factor de activitate ce reprezinta corectia fractiei molare pentru abaterea de la comportamentul perfect; 0 < i < 1.
Relatia (4.202) devine:
![]() (4.204)
(4.204)
Daca i = 1 atunci ai = xi.
In cazul solutiilor ideale diluate, fractia molara este proportionala cu concentratia molara ci, iar potentialul chimic al unui component va fi:
![]() (4.205)
(4.205)
Pentru solutiile reale (neideale) (ex.: solutii de electroliti tari) se introduce un alt factor de activitate fi:
ai = fici (4.206)
unde: ai = activitatea practica;
fi = factor de activitate ce reprezinta corectia concentratiei molare; 0 < fi < 1.
In ecuatiile potentialului chimic (4.201), (4.202), (4.204) si (4.205), potentialul chimic standard i reprezinta potentialul chimic in starea in care marimea pi, xi, ai sau ci are valoarea 1.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3248
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved