| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Solutii multicomponente de electroliti
Tratarea termodinamica a solutiilor multicomponente de electroliti a fost simplificata considerabil prin folosirea ecuatiilor care disting clar efectele de amestecare de cele ale componentilor puri.
Rush , Scatchard [131] si Guggenheim [129] au evidentiat ca aceasta maniera de tratare este facilitata de posibilitatile de utilizare a ecuatiilor analitice ce reprezinta cu acuratete proprietatile termodinamice ale electrolitilor puri.
Pitzer si colab. [33] [41] au stabilit pentru solutii de electroliti micsti un sistem de ecuatii care reprezinta o crestere "viriala" a energiei libere Gibbs de exces, GE, in functie de molalitatea ionilor, incluzand unele expresii provenite din consideratii teoretice si empirice stabilite pentru solutii cu un singur electrolit.
Forma ecuatiei initiale folosite de K. S. Pitzer si J. J. Kim este:
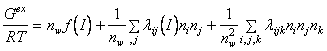 (A-14)
(A-14)
unde:
nw este nr. de kg. solvent,
ni , nj , nk , sunt numerele de moli de
specii ionice i, j si k. Functia f
depinde doar de taria ionica I si reprezinta ca si in modelul D-H, efectele
interactiilor coulombiene pe distanta mare. lij si ![]()
constituie al doilea si respectiv al treilea coeficient virial care reprezinta efectele fortelor pe distanta mica dintre ioni, considerati cate doi, respectiv cate trei in acelasi timp.
Functia "f" are forma matematica apropiata de functia conventionala de distributie D-H, conducand la aceeasi lege limita D-H, dar cu un efect mai mic al dimensiunii ionice. Dorind sa utilizeze o singura functie "f" independent de dimensiunea ionilor, autorii au acceptat o expresie aproximativa.
In cazul coeficientilor viriali, pe baza proprietatilor electrolitilor puri, au fost determinate sume adecvate. Proprietatile amestecurilor implica, adaugarea la aceste sume a altor termeni care dau seama de diferenta intre interactiile ionilor diferiti de acelasi semn si interactiile ionilor identici de acelasi semn. Daca s-ar respecta principiul lui Brnsted al interactiilor specifice [12], toti acesti termeni de diferenta ar fi zero. Pitzer si colab. [33] au renuntat la principiul lui Brnsted, si au aratat ca acesti termeni, desi mici ca marime si uneori neglijabili sunt in general mai mari ca zero.
Principalele caracteristici folosite de autori in stabilirea sistemului de ecuatii pentru solutii multicomponente au fost:
- considerarea electrolitilor sub forma ionizata si nu sub forma neutra, moleculara;
- dependenta coeficientului virial lij de taria ionica I, ceea ce face mai usoara adoptarea functiei "f" universale si obtinerea unei convergente mai rapide in seria viriala.
Astfel au stabilit ecuatii pentru coeficientul osmotic al amestecului de electroliti si pentru coeficientul de activitate al fiecarui electrolit neutru:
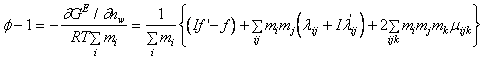 (A-15)
(A-15)
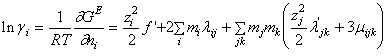 (A-16)
(A-16)
S-a notat ![]() si
si ![]() iar mi
= ni/nw
iar mi
= ni/nw
Pentru coeficientul de activitate al unui electrolit neutru se obtine:
 (A-16a)
(A-16a)
Pentru stabilirea setului de ecuatii (A-15), (A-16) si (A-16a) s-au folosit marimile:
![]() (A-6a)
(A-6a)
cu reluarea ecuatiei (A-7) si respectarea acelorasi semnificatii pentru marimi;
 (A-17)
(A-17)
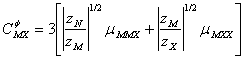 (A-13a)
(A-13a)
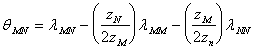
![]() (A-18)
(A-18)
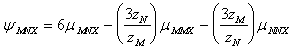 (A-19)
(A-19)
unde:
![]() este coeficientul Debye-Hckel ;
este coeficientul Debye-Hckel ; ![]() si are valoarea de 0.392 la 25 0C;
D este
si are valoarea de 0.392 la 25 0C;
D este
Pentru solutii multicomponente cu
ion comun de tip MX - NX sau cu valente superioare este necesar sa se adauge un
termen la parametrul ![]() care ia forma:
care ia forma:
![]() (A-20)
(A-20)
Pentru electroliti 2-2 valenti a = 1.4 si a = 12.0. Pe baza acestei noi adaugiri, tinand seama ca c si c' acopera toti cationii iar a si a' acopera toti anionii, se poate scrie ecuatia pentru coeficientul osmotic al solutiei sub forma:
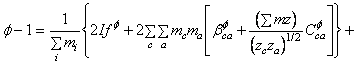
![]() (A-21)
(A-21)
unde: ![]()
In ecuatia (A-21) se regasesc termeni care reprezinta suma dubla pentru molalitati precum si pentru al doilea si al treilea coeficient virial in cazul unui electrolit pur. Acesti termeni pot fi evaluati din informatii asupra electrolitilor puri si au fost determinati pentru un numar mare de electroliti.
Pentru coeficientii de activitate
medii ionici ai solutiilor multicomponente de electroliti 2-2valenti sau cu
valente superioare se adauga la ![]() si
si ![]() parametri
parametri ![]() si a cu aceeasi forma ca in termenul
si a cu aceeasi forma ca in termenul![]() . Se obtine:
. Se obtine:
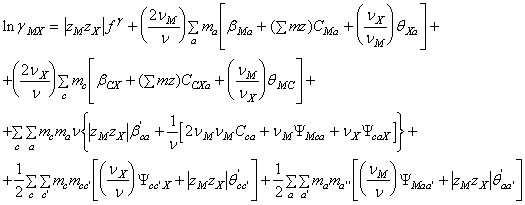
(A-22)
unde:
![]()
Ecuatia (A-22) capata forme simplificate in cazul in care toti dizolvatii sunt de acelasi tip de valenta, cand exista un anion sau un cation comun sau cand sunt doar doi dizolvati.
In cazul unui amestec de doi electroliti simetrici cu sarcina z si cu anion comun expresia coeficientului de activitate devine:
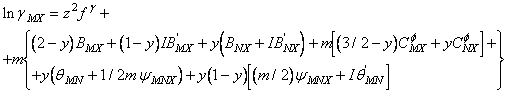 (A-23)
(A-23)
unde parametri :"f", b, C q si Y au semnificatiile date de ecuatiile: (A-6), (A-7), (A-10), (A-11), (A-12), (A-13), (A-17), (A-18) si (A-19).
Pe baza setului de ecuatii stabilit de Pitzer si colaboratori, Harvie, Moller si Weare [128] au stabilit un nou set de ecuatii in 1984, mult simplificat.
Ei au considerat ca in solutie electrolitul se regaseste sub forma de ioni, fiind astfel necesara tratarea termodinamica a ionilor individuali.
Coeficientul osmotic si coeficientii de activitate individuali devin:
 (A-24)
(A-24)
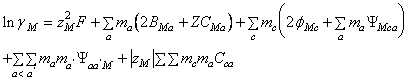 (A-25)
(A-25)
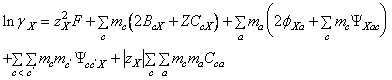 (A-26)
(A-26)
unde:
- m i este molalitatea (moli/Kg.solvent), M, c, c' indica cationi, X, a, a' indica anionii, c<c' si a<a' indica perechile deosebite de anioni si cationi,iar celelalte marimi au semnificatiile cunoscute.
AF si F sunt termeni definiti prin expresiile matematice indicate mai jos:
![]()
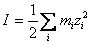 (A-27)
(A-27)
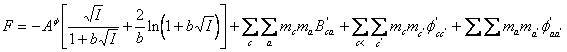
(A-28)
Parametri de interactie b b b (2) si CF definesc termenii B si C si au forme diferite in functie de numarul de electroliti din solutie si de valentele ionilor.
Astfel, pentru solutii ce contin o sare cu ioni mono-valenti acesti parametri au forma:
![]() ;
; ![]() ;
; ![]()
(A-29)
a=2 ; iar g(x) si g'(x) sunt functii de forma:
![]() ;
; ![]() ; (A-30)
; (A-30)
![]() ;
; ![]() ;
; ![]() ;
;
Pentru electroliti 2-2 valenti si de valente de tip superior sunt definiti urmatorii parametri:
![]() ;
; ![]()
![]() (A-29b)
(A-29b)
pentru
electroliti 2-2 valenti sunt valabili: ![]() ;
; ![]() , iar pentru electroliti de tip 3-2 si 4-2
valenti :
, iar pentru electroliti de tip 3-2 si 4-2
valenti :![]() ;
; ![]()
Harvie, Moller si
Weare considera ca pentru o solutie ce contine o singura sare proprietatile
termodinamice depind numai de parametri de interactie ![]() ,
, ![]() ,
, ![]() si
si ![]() . Parametri
f si y sunt utilizati numai pentru
amestecuri de minimum doua saruri. Parametrul f raspunde de interactiile cation-cation si
anion-anion, in timp ce parametrul y este definit pentru interactiile cation-cation-anion si
anion-anion-cation. Valorile fij sunt date de
relatiile:
. Parametri
f si y sunt utilizati numai pentru
amestecuri de minimum doua saruri. Parametrul f raspunde de interactiile cation-cation si
anion-anion, in timp ce parametrul y este definit pentru interactiile cation-cation-anion si
anion-anion-cation. Valorile fij sunt date de
relatiile:
![]() ;
; ![]() ;
; ![]() (A-31)
(A-31)
unde: qij este doar un parametru ajustabil si este definit pentru fiecare pereche de cationi si fiecare pereche de anioni.
Termenii ![]() si
si ![]() sunt responsabili
de efectele de amestecare electrostatice ale perechilor nesimetrice
cation-cation si anion-anion definite de Pitzer / /. Pentru ecuatii cu termeni electrostatici
de ordin superior acestia sunt calculati de fiecare data, utilizand aproximatia
Chebyshev [128] pentru perechi nesimetrice de anioni si cationi in integralele
de configuratie Pitzer. Valorile
sunt responsabili
de efectele de amestecare electrostatice ale perechilor nesimetrice
cation-cation si anion-anion definite de Pitzer / /. Pentru ecuatii cu termeni electrostatici
de ordin superior acestia sunt calculati de fiecare data, utilizand aproximatia
Chebyshev [128] pentru perechi nesimetrice de anioni si cationi in integralele
de configuratie Pitzer. Valorile ![]() si
si ![]() depind de sarcina si taria ionica si sunt zero
cand perechile de anioni si de cationi au aceeasi sarcina.
depind de sarcina si taria ionica si sunt zero
cand perechile de anioni si de cationi au aceeasi sarcina.
Coeficientul mediu ionic g poate fi calculat dupa ecuatia clasica:
![]() (A-32)
(A-32)
Rezultatele satisfacatoare obtinute de autori au permis extinderea utilizarii acestui set de ecuatii in caracterizarea termodinamica a apelor naturale [222].
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1555
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved