| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Calculul numeric al integralelor definite
Tematica lucrarii: 1. Generalitati;
2. Metoda trapezelor;
3. Metoda lui Simpson;
4. Metoda lui Gauss;
5. Programarea in MathCad;
6. Probleme de rezolvat;
7. Concluzii si intrebari.
1. Generalitati
Metodele de integrarea numerica utilizeaza formule de aproximare de diferite ordine. In general ordinul de aproximare reprezinta ordinul polinomului de interpolare pentru care formula este exacta, sau ordinul derivatei functiei de care depinde eroarea de aproximare. Trebuie mentionat ca ordinul formulei de integrare numerica nu ofera totdeauna garantia unei anumite margini de eroare, mai ales atunci cand functia de integrat are un mod de variatie mult diferit de cel al polinomului de interpolare corespunzator. Deaceea, de regula, domeniul de integrare se divizeaza intr-un anumit numar de subintervale. Pe fiecare dintre acestea se aplica apoi o anumita formula de integrare. Integrala globala rezulta ca o suma a integralelor pe subintervale.
Aplicarea procesului de integrare numerica se remarca prin trei aspecte importante:
a) alegerea diviziunii domeniului de integrare;
b) alegerea tipului de formula de integrare; (vit, posibilitati de evaluare a erorii)
c) alegerea ordinului formulei de integrare;
Cu cat functia de interpolat difera mai mult de polinomul de interpolare se prefera realizarea initiala a unei diviziuni mai fine, decat utilizarea unei formule de ordin ridicat. Alegerea formulei de integrare este determinata in functie de proprietatile de aproximare, dar si de complexitatea calculelor implicate sau posibilitatile de evaluare a erorii.
Pentru fiecare subinterval formulele de integrare utilizeaza o subdiviziune dependenta de ordinul formulei de integrare. In punctele subdiviziunii este evaluata functia de integrat. Unele formule de integrare numerica utilizeaza subdiviziuni uniforme, iar alte formule utilizeaza subdiviziuni neuniforme. Astfel, formula lui Simpson se bazeaza pe distante egale intre puncte, iar formula lui Gauss pe o distributie neuniforma a punctelor.
Este important de mentionat faptul ca desi se bazeaza pe un proces de aproximare formulele de calcul numeric reprezinta singura cale viabila de evaluare a integralelor. Determinarea analitica a primitivelor integralelor necesita rationamente complexe, iar in anumite cazuri acest proces este irealizabil.
2. Metoda trapezelor
Metoda trapezelor este cea mai simpla metoda de integrare numerica si se bazeaza pe interpolarea liniara a functiei de integrat f : [a,b] --> R pe fiecare subinterval al intervalului de definitie. Denumirea se datoreste suprafetelor trapezoidale formate intre abscisa si graficul functiei. Aproximand graficul functiei f(x) cu un segment de dreapta pe fiecare interval elementar [xk,xk ] se obtine relatia:
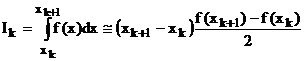 (1)
(1)
Daca aplicam acelasi procedeu in mod repetat pe intregul interval rezulta pentru valoarea totala a integralei:
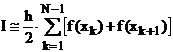 (2)
(2)
unde h reprezinta lungimea subintervalului h = xk+1- xk , iar N reprezinta numarul total de puncte ale diviziunii.
3. Metoda lui Simpson
Metoda Simpson utilizeaza interpolarea patratica pe fiecare subinterval. Curba de gradul doi ce aproximeaza functia f(x) este definita de cate trei puncte. Doua dintre puncte constituie capetele subintervalului, iar cel de-al treilea va fi considerat in mijlocul acestuia. Rezulta formula lui Simpson:
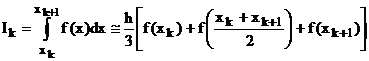 (3)
(3)
Daca aplicam acelasi procedeu in mod repetat pe intregul interval rezulta pentru valoarea totala a integralei:
 (4)
(4)
4. Metoda lui Gauss
Metoda Gauss utilizeaza o subdiviziune neuniforma de puncte in dorinta optimizarii formulei de integrare. Eroarea este minimizata atat prin alegerea distributiei punctelor de evaluare cat si prin alegerea ponderilor sumei de aproximare a integralei. Se poate demonstra ca daca utilizam n puncte de evaluare metoda este exacta pentru polinoame de grad 2n-1.
Metoda este definita numai pe intervalul [-1,1]. Pentru un interval oarecare de integrare se foloseste relatia de transformare:
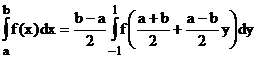 (5)
(5)
Formula lui Gauss realizeaza aproximarea integralei sub forma unei sume ponderate:
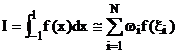 (6)
(6)
unde ponderile i si i sunt determinate si tabelate pentru formulele de diferite ordine.
5. Programarea in MathCad
Sa definim intervalul de integrare prin variabilele a si b. Daca numarul total de puncte este N, atunci pasul de integrare h este h := (a-b)/N . Consideram variabilele sir j := 0..N-1 si
k := 1..4. Rezulta ca punctele diviziunii xj au valorile xj := h j . Atunci se pot scrie relatiile corespunzatoare sumelor de aproximare a integralelor pentru fiecare tip de formula. Rezulta atfel procedurile corespunzatoare pentru:
Formula trapezelor:
![]() (7)
(7)
Formula lui Simson:
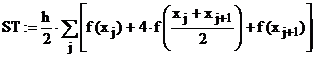 (8)
(8)
Formula lui Gauss cu patru puncte de evaluare:
 (9)
(9)
In cazul formulei lui Gauss cu patru puncte ponderile k si k au valorile urmatoare:
; (10)
; (11)
Functia f trebuie definita inainte de formulele de calcul ale integralelor, considerand o variabila oarecare. Functia nu trebuie sa contina puncte singulare (pentru care ia valoare infinita) pe parcursul intervalului de integrare. Se va alege o functie a carei integrala nedefinita sa aiba o primitiva cunoscuta. Acest lucru va permite o verificare mai usoara a rezultatelor obtinute. Verificarea numerica se va realiza prin utilizarea comenzii de integrare MathCad existente in cadrul programului.
Numarul
de puncte ale diviziunii
6. Probleme de rezolvat
In aplicatiile din domeniul electric informatiile referitoare la curent sau tensiune sunt de multe ori utilizate ca valori medii sau valori efective. In acest caz este necesara efectuarea unei operatii de integrare. S-a dovedit din mai multe puncte de vedere ca prelucrarea numerica este preferabila. In aplicatia de mai jos sunt comparate rezultatele obtinute in urma integrarii numerice a unei functii-semnal caracterizata printr-o anumita componenta de armonici si trasata grafic in fig.1.
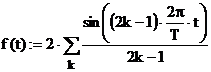 (12)
(12)
unde t este variabila independenta (timpul);
k := 1..5 reprezinta ordinul armonicii continute in semnal;
T := 0.010 (s) este perioada semnalului (de 50 de Hz).
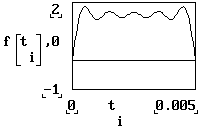 Fig.1
Variatia unui semnal continand armonici
Fig.1
Variatia unui semnal continand armonici
Graficul trasat contine 100 de esantioane, si este trasat pe durata unei semiperioade (5ms).
Pentru integrarea functiei semnal f(t) pe intervalul corespunzator graficului au fost utilizate cele trei formule numerice prezentate mai sus. Fiecare formula a fost aplicata in mod repetat pe un numar de 10 subintervale. In continuare sunt dat valorile obtinute (notate respectiv cu ST, SS, SG) si erorile relative (notate respectiv ET, ES, EG) fata de valoarea obtinuta cu procedura de integrare (adaptiva) a programului Mathcad:
Formula trapezelor: ST = 0.007258 ET = 0.0037 (13)
Formula lui Simpson: SS = 0.007541 ES = 6.459 10 (14)
Formula lui Gauss: SG = 0.007536 EG = 7.548 10 (15)
Se cere:
Realizarea graficului functiei de integrat;
Implementarea in limbaj MathCad a algoritmilor de integrare prezentati mai sus;
Analiza erorilor de aproximare pentru metodele date, in functie de modul de diviziune a intervalului de integrare.
7. Concluzii
a) Metodele de integrare numerica bazate pe principii si formule de calcul mai complexe au o precizie sporita, insa aceasta este garantata de regula pentru anumite tipuri de functii, cum sunt cele polinomiale. Astfel metoda lui Gauss de ordinul n devine exacta pentru polinoame de ordinul 2n-1. Totusi in anumite cazuri, cand functia de integrat are o variatie mult diferita de cea polinomiala rezultatele pot fi modeste. Daceea uneori este de preferat utilizarea unor formule de integrare mai simple, bazate pe un numar mai mic de puncte de evaluare ale functiei (cum este metoda trapezelor) si aplicate pe subintervale de intindere mai redusa, dar mai numeroase.
b) Programele de firma utilizeaza metode de integrare adaptiva aplicabile pentru clase largi de functii. Aceste proceduri realizeaza comparatii ale rezultatelor obtinute atunci cand pasul este modificat. Cu cat aceste teste se realizeaza mai des pe parcursul intervalului de integrare cu atat viteza de lucru a programului scade.
c) Eroarea produsa de procedurile de integrare numerica se poate cumula atunci cand intervalul de integrare are intindere mare. De aceea se recomanda ca in astfel de cazuri diviziunea subintervalelor sa nu contina un numar exagerat de puncte.
d) Una dintre aplicatiile importante ale integraii numerice este rezolvarea problemelor continue, cum ar fi determinarea potentialului electric intr-un anumit domeniu. Discretizarea acestor probleme presupune considerarea unui numar finit de puncte, destul de redus, in care este calculata solutia. Prin discretizarea problemei se obtine de regula un sistem de ecuatii algebrice ai carui coeficienti sunt integrale definite. Se pune astfel problema calculului numeric a unui numar mare de integrale (corespunzator numarului de puncte considerate in forma discreta a problemei). In aceasta situatie trebuie realizat un compromis intre precizia si viteza metodei numerice alese. Deseori este utilizata metoda lui Gauss cu patru puncte prezentata mai sus.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5997
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved