| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Oscilatii si unde
Notiuni generale
Se numeste oscilatie fenomenul fizic in decursul caruia o anumita marime fizica a procesului prezinta o variatie periodica sau pseudo-periodica. Un sistem fizic izolat, care este pus in oscilatie printr- un impuls, efectueaza oscilatii libere sau proprii, cu o frecventa numita frecventa proprie a sistemului oscilant. Oscilatiile pot fi clasificate in functie de mai multe criterii.
Din punct de vedere al formei de energie dezvoltata in timpul oscilatiei, putem intalni: (i) oscilatii elastice, mecanice (au loc prin transformarea reciproca a energiei cinetice in energie potentiala); (ii) oscilatii electromagnetice (au loc prin transformarea reciproca a energiei electrice in energie magnetica);
(iii) oscilatii electromecanice (au loc prin transformarea reciproca a energiei mecanice in energie electromagnetica).
Din punct de vedere al conservarii energiei sistemului oscilant, putem clasifica oscilatiile in: (i) oscilatii nedisipative, ideale sau neamortizate (energia totala se conserva); (ii) oscilatii disipative sau amortizate (energia se consuma in timp) (iii) oscilatii fortate sau intretinute (se furnizeaza energie din afara sistemului, pentru compensarea pierderilor).
Marimi caracteristice oscilatiilor periodice
Sa notam cu S(t) marimea fizica ce caracterizeaza o oscilatie. Atunci, daca T este perioada oscilatiei, marimea S are aceai valoare la momentul t si la un moment ulterior, t + T:
S(t) = S(t+T )
Oscilatiile armonice reprezinta acel tip de oscilatii in care marimile caracteristice se pot exprima prin functii trigonometrice (sinus, cosinus ) sau prin functii exponentiale de argument complex. Acele oscilatii care nu sunt armonice, se pot descompune in serii Fourier de functii. Reamintim, de asemenea, formulele lui Euler, care vor fi utile in calculele urmatoare:
Miscarea oscilatorie armonica apare foarte des in situatiile practice. Un exemplu foarte la indemana il constituie bataile inimii. Se spune ca Galilei folosea bataile inimii sale pentru a cronometra miscarile pe care le studia.
Micarea oscilatorie armonica ideala
In absenta unor forte de frecare sau de disipare a energiei, miscarea oscilatorie este o miscare ideala, deoarece energia totala a oscilatorului ramane constanta in timp. Micarea este reversibila, astfel ca dupa o perioada oscilatorul revine in pozitia initiala si procesul se reia. Forta care determina revenirea oscilatorului in pozitia initiala si care permite continuarea oscilatiei se numete forta de revenire. Aceasta forta de revenire poate fi forta elastica dint-o lama metalica, presiunea dintr-un tub si, in general, orice forta care produce o deformare elastica.
Sa consideram un oscilator mecanic format dintr-un resort elastic si un corp punctiform, de masa m, legat la capatul liber al resortului, ca in fig.1.a. Daca se pune corpul in miscare prin intermediul unei forte si daca nu exista frecari, sistemul va efectua o micare periodica in jurul pozitiei de echilibru, numita oscilatie ideala.
Forta elastica din resort, eF , este singura forta din sistemul mecanic, aa ca putem scrie formula fudamentala a dinamicii sub forma:
ma = - k y
unde k este
Ecuatia de micare a corpului devine:
m a + k y = 0
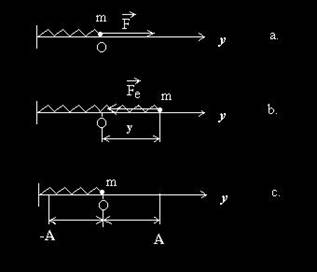
Fig. Oscilator mecanic ideal a) momentul initial b) alungirea y produce forta de revenire eF
c) amplitudinea micarii oscilatorii.
Acceleratia corpului reprezinta derivata de ordinul doi la timp a vectorului deplasare, de aceea ecuatia de micare devine:
Reprezentarea marimilor vectoriale periodice se poate realiza si prin intermediul fazorilor. Fazorul este un vector rotitor in sens trigonometric pozitiv intr-un plan Oxy, care are vitexa unghiulara
. Lungimea fazorului este egala cu modulul vectorului pe care il reprezinta, adica fazorul este egal cu amplitudimea micarii oscilatorii. Faza vectorului reprezentat este egala cu unghiul format de fazor cu axa orizontala, Ox. Vectorul reprezentat este egal cu proiectia fazorului pe axa verticala Oy. Fazorul din fig. 2 reprezinta elongatia oscilatorului ideal, in diferite momente de timp.
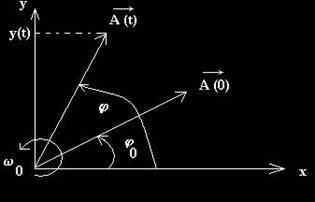
Fig. 2. Reprezentarea fazoriala a oscilatiei
Marimile fizice caracteristice ale oscilatorului ideal pot fi reprezentate grafic in functie de timp. Daca faza initiala este nula, se obtin graficele functiilor y = f(t , v = f(t) si a = f(t) din fig.
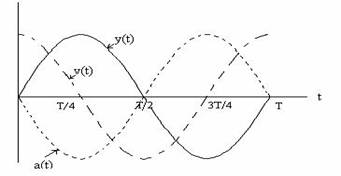
Fig. Elongatia, viteza si acceleratia oscilatorului ideal in functie de timp
Energia mecanica a oscilatorului ideal este constanta, ceea ce constitue legea conservarii energiei mecanice a oscilatorului ideal.
In decursul oscilatiei ideale,
energiile cinetica si
potentiala elastica ale oscilatorului ideal sunt variabile in timp, transformandu-se una in alta, in aa fel incat suma lor sa ramana constanta. In fig.4 sunt reprezentate energiile cinetica, potentiala si
totala in functie
de elongatia y. Se poate
observa ca desi energia potentiala
este variabila, fiind reprezentata de parabola din figura, totusi energia mecanica a oscilatorului ideal este
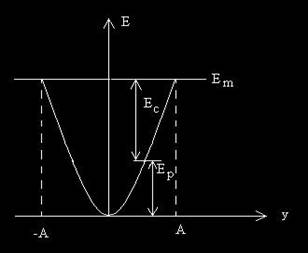
Fig.4. Energiile cinetica, potentiala si totala in functie de elongatia oscilatorului ideal.
Conservarea energiei mecanice a oscilatorului constituie efectul direct al faptului ca fortele elastice sunt forte conservative. Caracterul oscilant al miscarii se poate constata si din transformarea periodica a energiei cinetice in energie potentiala si reciproc.
Compunerea miscarilor oscilatorii armonice
Pe baza legilor micarii oscilatorii armonice ideale se pot studia miscari oscilatorii mai complexe, care rezulta din compunerea a doua sau mai multe oscilatii armonice, care se desfasoara pe directii paralele sau pe directii perpendiculare.
1. Compunerea oscilatiilor armonice paralele de aceeasi pulsatie
Sa presupunem ca un punct material
de masa m
este legat de doua resorturi elastice, aa cum se vede in
fig.5, fiind supus simultan la
doua forte elastice pe aceeai
directie dar in sensuri diferite. Cele doua
resorturi elastice sunt identice, adica au
aceeai
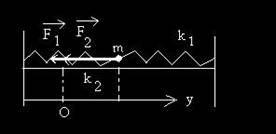
Fig.5. Oscilatie armonica sub actiunea a doua forte elastice paralele.
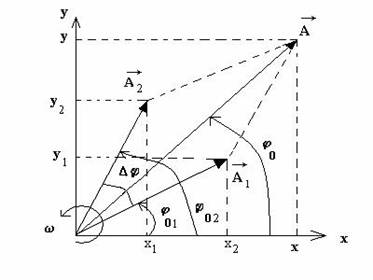
Fig. 6. Reprezentarea fazoriala a compunerii oscilatiilor paralele.
2. Compunerea oscilatiilor armonice paralele de frecventa diferita
Consideram doua oscilatii armonice individuale ale punctului material de masa m. Una dintre oscilatii are pulsatia proprie iar cealalta are pulsatia proprie 2. Diferenta dintre cele doua frecvente de oscilatie nu este insa prea mare. Elongatiile celor doua oscilatii armonice independente sunt de forma:
Punctul material este supus simultan ambelor oscilatii, asa cum se poate vedea in fig. 7, si ne propunem sa determinam ecuatia oscilatiei rezultante.
Fig. 7. Compunerea a doua oscilatii paralele de frecvente diferite.
Tb mai este numita si perioada batailor.
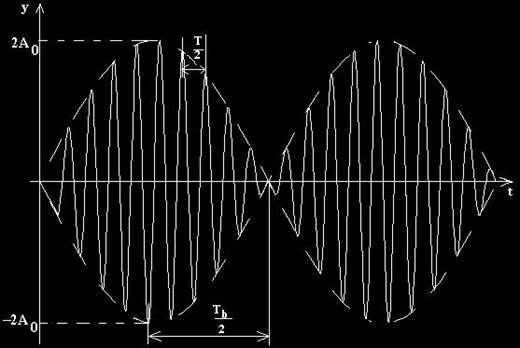
Fig. 8. Fenomenul de batai.
Faza oscilatiei are perioada T, mult mai mica decat Tb:
Oscilatia rezultanta este reprezentata, in fig.7, cu linie continua.
Perioada batailor este intervalul de timp intre doua treceri succesive ale amplitudinii rezultante prin valoarea minima sau maxima.
Compunerea oscilatiilor perpendiculare
Consideram un punct material de masa m, care care este solicitat simultan sa oscileze armonic sub actiunea a doua resorturi elastice identice legate pe doua directii perpendiculare, ca in fig. 9.
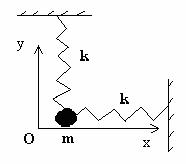
Fig. 9. Compunerea oscilatiilor perpendiculare
Cele doua miscari oscilatorii armonice sunt perpendiculare, avand ecuatiile elongatiilor pe cele doua directii de forma
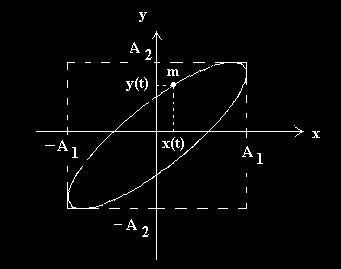
Fig. 10. Traiectorie eliptica rotita fata de axe.
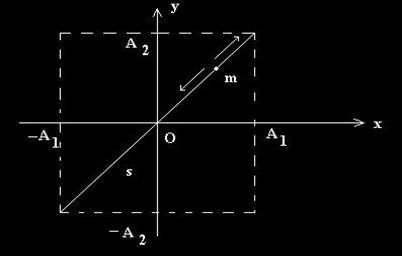
Fig. 11. Traiectorie particulara in cazul compunerii oscilatiilor perpendiculare in faza,
Elipsa care descrie traiectoria particulei nu mai este rotita fata de axele de coordonate (vezi fig.12).
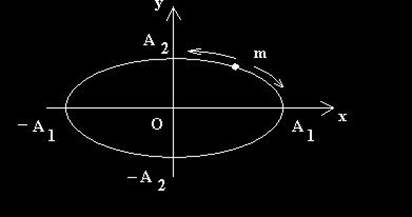
Fig.12. Traiectoria rezultata din compunerea a doua oscilatii perpendiculare in cuadratura de faza,
Micarea punctului material se defasoara pe elipsa, intr-un sens sau in altul.
4. Miscarea oscilatorie amortizata
Sistemele oscilante reale sunt supuse unor forte de franare, sau de disipare a energiei pe care-o au la inceputul miscarii. Acea parte a energiei ce se pierde prin frecare se transforma in caldura. Ampltudinea micarii oscilatorii amortizate este scazatoare in timp. Un caz interesant de forte de franare il constituie fortele proportionale cu viteza de oscilatie. Micarea este neperiodica, aa cum se vede in fig. 1 Elongatia tinde la zero cand timpul tinde la infinit, fara ca punctul material sa oscileze.
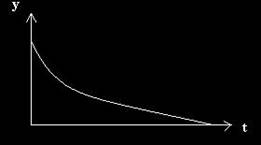
Fig. 1 Elongatia micarii cu forta de amortizare mare, 0 .

Fig. 14. Elongatia si amplitudinea oscilatorului armonic amortizat in functie de timp.
Observam ca oscilatia amortizata este modulata in amplitudine. Elongatia tinde la zero cand timpul tinde la infinit, punctul material osciland in jurul pozitiei de echilibru cu o amplitudine din ce in ce mai mica.
Descreterea amplitudinii micarii oscilatorii amortizate este caracterizata de marimea numita decrement logaritmic. Decrementul logaritmic este egal cu logaritmul natural al raportului dintre doua amplitudini succesive:
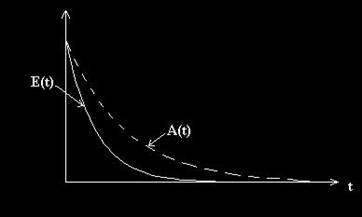
Fig. Dependenta de timp a energiei mecanice si a amplitudinii oscilatorului amortizat.
5. Analogie intre oscilatiile mecanice si cele electromagnetice
Examinand oscilatiile elastice (ale unui sistem format dintr-un resort elastic si un corp punctiform) si oscilatiile electromagnetice (dintr-un circuit serie RLC de curent alternativ), constatam o serie de asemanari (similitudini). Aceste asemanari au condus la stabilirea unor corespondente intre marimile electrice si cele mecanice, adica la stabilirea unor analogii intre aceste marimi. Cunoaterea analogiilor dintre marimile electrictromagnetice si cele mecanice permite transpunerea rezultatelor obtinute pentru oscilatiile elastice armonice (ideale sau amortizate) la cazul oscilatiilor electrice. Consideram un circuit serie RLC, format dintr-un rezistor cu rezistenta electrica R, o bobina ideala cu inductanta L, si un condensator de capacitate electrica C (vezi fig. 16).
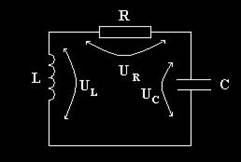
Fig. 16. Circuit RLC parcurs de un curent electric variabil in timp.
Consideram ca bobina constituie secundarul unui transformator. In bobina se induce o tensiune electromotoare, uL, prin inductie electromagnetica intre primarul si secundarul transformatorului. Similitudinile dintre cele doua tipuri de oscilatii sunt prezentate in Tabelul 1. Astfel, putem observa ca toate marimile fizice corespunzatoare oscilatiei electromagnetice au un corespondent in marimi corespunzatoare oscilatiei elastice. Folosind analogia dintre oscilatiile amortizate ale resortului elastic si oscilatiile electromagnetice amortizate din circuitul RLC, se poate scrie intensitatea instantanee a curentului electric din circuit, care este data de relatia:
In fig. 17 se prezinta intensitatea instantanee a curentului electric din circuit si amplitudinea oscilatiilor sale in functie de timp.
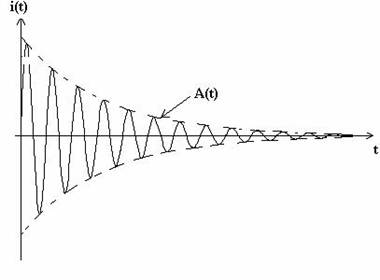
Fig. 17. Intensitatea instantanee a curentului electric din circuitul oscilant amortizat.
6 Oscilatii fortate. Rezonanta
Sa consideram un oscilator mecanic format dintr-un resort elastic si un corp de dimensiuni neglijabile. Datorita fortei de frecare, energia mecanica a oscilatorului se consuma in timp, astfel incat oscilatia este amortizata, aa cum am vazut in paragraful 4. Pentru a intretine miscarea oscilatorie,trebuie sa se aplice forte exterioare (numite forte de fortare), care sa compenseze pierderile de energie din sistem In acest caz, punctul material va efectua o miscare oscilatorie fortata. Dintre tipurile de forte de fortare (sau perturbatoare) ce se pot aplica sistemului oscilant, un caz interesant pentru aplicatiilepractice este cel in care fortele perturbatoare sunt periodice.
Experienta arata ca o miscare periodica intretinuta prezinta un regim tranzitoriu, dupa trecerea caruia se instaleaza regimul permanent. Regimul tranzitoriu este de scurta durata, iar regimul permanent se manifesta prin oscilatii intretinute.
6.1. Rezonanta
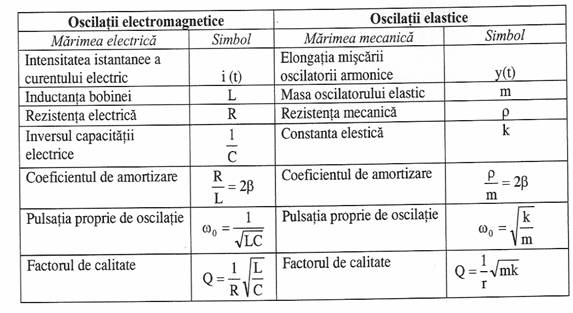
Aa cum am vazut in paragraful anterior, dupa stabilirea regimului permanent al oscilatiei intretinute, frecventa de oscilatie este egala cu frecventa fortei perturbatoare. Sistemul oscilant adopta pulsatia fortei perturbatoare, care este diferita de pulsatia sa proprie de oscilatie ca sistem
Rezonanta este fenomenul fizic de aparitie a maximului amplitudinii oscilatiei intretinute. Sistemul fizic aflat la rezonanta oscileaza cu amplitudine maxima. Deci,din punct de vedere fizic, este ideal sa amplificam la maxim o oscilatie armonica, totusi in practica trebuie evitate situatiile in care frecventa fortei de intretinere coincide cu frecventa proprie a oscilatorului,deoarece in acest caz amplitudinea tinde la infinit. Rezonanta mecanica are multiple aplicatii in tehnica.

Fig. 18. Curbe de rezonanta pentru diferite valori ale coeficientului de amortizare:
Astfel, in acest paragraf am constatat ca in cazul oscilatiilor intretinute, sau fortate, forta exterioara produce un lucru mecanic ce compenseaza pierderile de energie din sistemul oscilant. In paragraful urmator vom vedea cum se caracterizeaza din punct de vedere energetic oscilatiile intretinute.
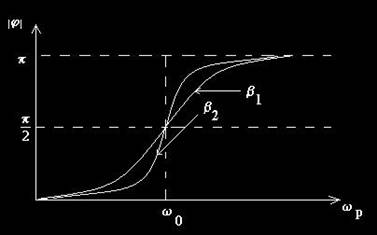
Fig. 19. Variatia modulului fazei intiale a oscilatiei permanente in
6.2. Consideratii energetice ale oscilatiilor fortate
In continuare vom defini cateva marimi fizice care caracterizeaza transferul energiei mecanice in sistemul ce efectueaza oscilatii fortate, sau intretinute.
1. Puterea instantanee absorbita de sistemul oscilant intretinut reprezinta derivata la timp a lucrului mecanic efectuat de forta de fortare.
2. Puterea medie absorbita in decursul unei perioade reprezinta integrala pe o perioada a puterii instantanee absorbite Pa (t).
Puterea instantanee disipata sub forma de caldura de catre forta de frecare reprezinta derivata la timp a lucrului mecanic efectuat de forta de frecare.
4.Puterea medie disipata intr-o perioada reprezinta integrala pe o perioda a puterii instantanee disipate.
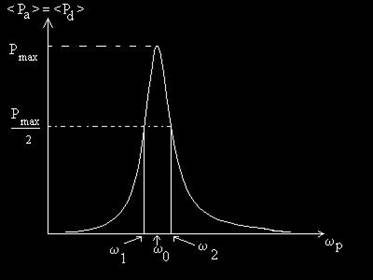
Fig. 20. Puterile medii absorbita si disipata
Oscilatii armonice
Un corp efectueaza oscilatii armonice atunci cand asupra lui actioneaza o forta de tip elastic:
F = - k x,
k -
![]() , ω0 - pulsatie
proprie;
, ω0 - pulsatie
proprie; ![]() , T0 -perioada proprie;
, T0 -perioada proprie;
x(t) = A sin (ω0 t + φ);
Oscilatii amortizate:
Oscilatiile unui corp sunt amortizate atunci cand asupra lui actioneaza, pe langa forta de tip elastic (- k x) si o forta rezistenta proportionala cu viteza (- α v):
F = - k x - α v, α -coeficient de rezistenta;
![]()
![]() , ω -pulsatia
oscilatiei amortizate;
, ω -pulsatia
oscilatiei amortizate;
β -factor de amortizare;
Observatie:
Avem de-a face cu
miscare de oscilatie numai daca ![]() .
.
x(t) = A e - β t sin (ω t + φ);
![]() -
decrement logaritmic;
-
decrement logaritmic;
T - perioada miscarii oscilatorii amortizate.
Oscilatii fortate
Forta care intretine oscilatia este sinusoidala de amplitudine F0 si pulsatie ω1:
F = - k x - α v + F0 sin (ω1 t);
x(t) = A1 sin (ω1 t - φ1 )
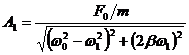
![]() ;
;
A1
(ω1) = maxima ![]() ω1=
ωrez =
ω1=
ωrez =![]() .
.
O particula efectueaza
oscilatii sinusoidale de-a lungul axei Ox in jurul pozitiei de
echilibru. Pulsatia oscilatiilor este ω = 5 rad/s. La momentul t0=0
particula se gaseste in pozitia x0 = 12 cm si are viteza ![]() =0,6 m/s.
Determinati legea de miscare si legea vitezei.
=0,6 m/s.
Determinati legea de miscare si legea vitezei.
R: ![]() cm;
cm; ![]() m/s.
m/s.
Determinati pulsatia si amplitudinea oscilatiilor sinusoidale efectuate de o particula daca la distantele x1 si x2 de la pozitia de echilibru viteza particulei are valorile v1 si v2.
R: 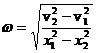 ,
, 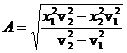 .
.
Un corp de masa m = 0,05 kg fixat de capatul unui resort de
a) legea de miscare;
b) energia totala a corpului.
R: a) x(t) = 0,03 sin(20 t) m; b) Et = 910 -3 J.
Un corp de masa m = 0,05 kg fixat de capatul unui resort executa o miscare oscilatorie armonica de-a lungul axei Ox dupa legea:
![]() m. Sa se determine:
m. Sa se determine:
a)
b) energia totala a corpului;
c) momentele de timp la care energia cinetica este egala cu energia potentiala.
R:
a) k = 5 N/m, ![]() s; b) Et
= 6.2510 -3 J; c)
s; b) Et
= 6.2510 -3 J; c) ![]() s, unde n=numar natural.
s, unde n=numar natural.
Un punct material efectueaza o miscare oscilatorie amortizata de-a lungul axei Ox. Perioada miscarii este T=3 s, iar decrementul logaritmic δ=0,6. Sa se scrie legea de miscare, stiind ca la momentul initial t0 = 0, x0 = 0, v0 = 0,5 m/s.
R:
![]() .
.
Sa se scrie expresia vitezei oscilatiilor amortizate.
Rezolvare:
x(t) = A0 e - β t sin (ω t + φ),
![]()
![]() ,
,
![]()
![]() ;
;
![]()
![]() ,
,
![]()
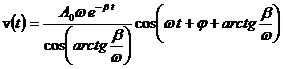
Un punct material executa oscilatii amortizate cu pulsatia ω. Sa se determine coeficientul de amortizare β daca la momentul t0 = 0 viteza punctului material este nula, iar elongatia este de n ori mai mica decat amplitudinea.
R:
![]() .
.
Un corp oscileaza intr-un mediu cu decrementul logaritmic δ1. Care este decrementul logaritmic δ2 daca coeficientul de rezistenta al mediului creste de n ori?
Rezolvare:
![]()
![]()
![]() ;
;
![]()
![]() ,
,
![]()
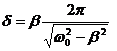
![]()
![]() ;
;
![]()
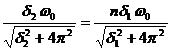 ,
,
![]()
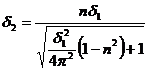 .
.
Un corp oscileaza intr-un mediu cu decrementul logaritmic δ1. De cate ori trebuie sa creasca rezistenta mediului pentru ca oscilatia amortizata sa devina miscare amortizata aperiodica (β2 = ω0).
R:
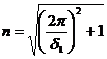 .
.
Un corp de masa m=250 g executa o miscare de
oscilatie amortizata cu factorul de amortizare β = π/4 s - 1, perioada oscilatiilor
proprii fiind ![]() s.
Oscilatiile corpului devin fortate in urma actiunii unei
forte exterioare periodice
s.
Oscilatiile corpului devin fortate in urma actiunii unei
forte exterioare periodice ![]() N. Sa se
scrie elongatia oscilatiilor fortate.
N. Sa se
scrie elongatia oscilatiilor fortate.
R: ![]() m.
m.
Amplitudinea oscilatiilor fortate este aceeasi pentru doua frecvente ν1 si ν2. Sa se afle frecventa de rezonanta a oscilatiilor.
R: ![]() .
.
Asupra unui corp, care efectueaza o miscare oscilatorie amortizata cu perioada oscilatiilor proprii T0, actioneaza o forta exterioara sinusoidala de amplitudine F0. La rezonanta vitezelor, amplitudinea oscilatiilor este A0. Sa se afle coeficientul de rezistenta.
Rezolvare:
x(t)=A1 sin (ω1 t - φ1 ) - legea de oscilatie in cazul oscilatiilor fortate;
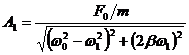
v(t)=A1 ω1 cos (ω1 t - φ1 )
Rezonanta vitezelor se realizeaza atunci cand :
ω1 A1=
maxima ![]()
![]()
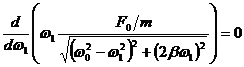
![]() ω1
= ω0
ω1
= ω0
![]()
![]() ;
;
Dar
![]() , iar
, iar ![]()
![]()
![]() .
.
Un corp care efectueaza o miscare oscilatorie fortata are amplitudinea vitezei egala cu 1/3 din amplitudinea vitezei la rezonanta vitezelor, pentru doua pulsatii ω1 si ω2. Sa se afle:
a) pulsatia proprie a oscilatorului ω0;
b) factorul de amortizare β.
R: a) ![]() ; b)
; b) ![]() .
.
Compunerea oscilatiilor armonice paralele
a) Oscilatii cu aceeasi pulsatie
x1 (t) = A1 sin (ω t + φ1),
x2 (t) = A2 sin (ω t + φ2);
Rezultatul compunerii a doua oscilatii armonice paralele de aceeasi pulsatie este tot o oscilatie armonica de aceeasi pulsatie pe aceeasi directie.
x (t) = x1 (t) + x2
(t) ![]() x (t) =
A sin (ω t + φ)
x (t) =
A sin (ω t + φ)
![]() ,
, ![]() .
.
b) Oscilatii cu pulsatii putin diferite
Rezultatul compunerii a doua oscilatii armonice paralele de pulsatii diferite nu mai este o oscilatie armonica.
x1 (t) = A sin (ω1 t + φ1),
x2 (t) = A sin (ω2 t + φ2),
x (t) = x1 (t) + x2 (t) ;
Daca pulsatiile sunt foarte apropiate intre ele, iar amplitudinile oscilatiilor care se compun sunt egale, oscilatia rezultanta este aproape sinusoidala:
![]()
In cazul frecventelor
acustice sunetul de pulsatie ![]() se aude
succesiv, intarindu-se si slabindu-se cu pulsatia si
perioada batailor:
se aude
succesiv, intarindu-se si slabindu-se cu pulsatia si
perioada batailor: ![]() .
.
Compunerea oscilatiilor armonice perpendiculare
a) Oscilatii cu aceeasi pulsatie
x (t) = A1 sin (ω t + φ1),
y (t) = A2 sin (ω t + φ2);
Traiectoria
unui punct material supus simultan la doua oscilatii armonice
perpendiculare de aceeasi pulsatie este o elipsa a carei
forma depinde de ![]() :
:
![]()
b) Oscilatii cu pulsatii diferite
Un
punct material supus simultan la doua oscilatii armonice
perpendiculare de pulsatii diferite are o traiectorie complicata.
Daca raportul pulsatiilor este un numar rational
traiectoria este una din figurile Lissajous, forma traiectoriei depinzand
si de diferenta de faza ![]() .
.
Un punct material este supus simultan la doua miscari oscilatorii armonice descrise de legile:
x1 (t) = 1,2 sin ![]() m,
respectiv x2 (t) = 1,6 sin
m,
respectiv x2 (t) = 1,6 sin![]() m.
m.
Sa se scrie legea de miscare rezultanta.
R:
x (t) = 2 sin (![]() t + 0,37 π) m.
t + 0,37 π) m.
Un punct material este supus simultan la doua miscari oscilatorii armonice descrise de legile:
a) ![]() m,
m, ![]() m;
m;
b) ![]() m,
m, ![]() m;
m;
c) ![]() m,
m, ![]() m.
m.
Sa se determine ecuatia traiectoriei punctului material, precizandu-se forma acesteia.
R: a) ![]() , traiectoria este o dreapta; b)
, traiectoria este o dreapta; b) ![]() , traiectoria este o elipsa avand drept axe chiar
axele de coordonate; c)
, traiectoria este o elipsa avand drept axe chiar
axele de coordonate; c) ![]() , traiectoria este un cerc.
, traiectoria este un cerc.
Sa se determine ecuatia traiectoriei unui punct material supus simultan la doua miscari oscilatorii:
a) x (t) = A sin (ω t), y (t) = A sin (2ω t);
b) x (t) = A sin (ω t), y (t) = A cos (2ω t).
Rezolvare:
a)
x = A sin (ω t)![]()
![]()
y
= Asin(2ωt) ![]() y = 2A sin
(ω t) cos (ω t),
y = 2A sin
(ω t) cos (ω t),
![]()
![]()
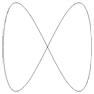
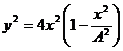 - traiectoria este una din figurile Lissajous:
- traiectoria este una din figurile Lissajous:
b) Cele doua oscilatii care se compun au acelasi raport al pulsatiilor ca si la punctul a), dar defazajul este altul si deci forma traiectoriei este alta.

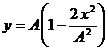
7. Unde elastice
Mediile continue, cum sunt solidele, lichidele si gazele, sunt medii formate din particule (atomi, molecule sau ioni) care interactioneaza intre ele. De aceea, daca una dintre particule oscileaza (vibreaza), atunci vor oscila (vor vibra) si particulele vecine; in felul acesta oscilatiile (perturbatiile) se propaga prin mediu de la o particula la alta. Prin propagarea oscilatiilor se genereaza undele.
Unda reprezinta fenomenul de extindere si propagare din aproape in aproape a unei perturbatii periodice produse intr-un anumit punct din mediul de propagare. Propagarea undei se face cu o viteza finita, numita viteza undei. Unda nu reprezinta transport de materie, ci numai transport de energie.
Dupa tipul de energie pe care-l transporta unda, putem deosebi: (i) unde elastice (se transporta energie mecanica, undele fiind generate de perturbatiile mecanice ale mediilor elastice), (ii) unde electromagnetice (se transporta energie electromagnetica) (ii) unde magneto-hidrodinamice (sunt generate prin perturbatii electromagnetice si elastice ale mediului de propagare).
Dupa natura perturbatiei si modul de propagare al acesteia, putem clasifica undele in: (1) unde
longitudinale (directia de propagare a undei coincide cu directia de oscilatie); (2) unde transversale
(directia de propagare a undei este perpendiculara pe directia de oscilatie).
O marime deosebit de importanta pentru descrierea undei este functia de unda, pe care o putem nota in mod generic cu (x y,z,t). Functia de unda reprezina functia matematica ce descrie marimea perturbata.
Suprafata de unda reprezinta multimea punctelor din spatiu ce oscileaza avand la un moment dat aceeai valoare a functiei de unda, (x,y,z,t) constant = a. Dupa forma suprafetelor de unda, putem intalni unde plane, unde sferice, unde cilindrice, etc.
Frontul de unda reprezinta suprafata de unda cea mai avansata la un moment dat.
7.1. Unde armonice unidimensionale
Fig. 21. Oscilatia generata in originea axei Ox se propaga pana in punctul M.
Constam ca ecuatia elongatiei yM(x, t) a oscilatiei dintr-un punct oarecare M, aflat pe directia de propagare a undei, are o intarziere de faza, dependenta de pozitia sa fata de sursa undei. Cu cat punctul M se afla mai departe de originea undei, cu atat mai tarziu va intra in oscilatie; oscilatia din punctul considerat va avea o intarziere de faza mai mare, daca punctul este mai departe de sursa undei.
Vectorul de unda este marimea fizica vectoriala orientata in sensul propagarii undei. Vectorul de unda materializeaza directia in care se propaga energia undei. Utilizand vectorul de unda, putem scrie ecuatia elongatiei oscilatiei din punctul M sub forma:
7.2. Consideratii energetice asupra propagarii undei
Propagarea unei unde elastice intr-un anumit mediu genereaza o serie de miscari de oscilatie ale particulelor mediului; punctele materiale ii incep micarea oscilatorie, in jurul pozitiiilor lor de echilibru, pe masura ce energia undei ajunge pana la ele.
Fig. 22. Densitatea volumica de energie intr-un punct al mediului de propagare si densitatea volumica medie de energie
Alte marimi ce sunt utilizate pentru a descrie energia transportata de unda sunt urmatoarele:
a). Fluxul de energie. Fluxul de energie reprezinta cantitatea de energie transmisa printr-o suprafata in unitatea de timp, fiind dat de derivata energiei la timp.
b). Densitatea flluxului de energie reprezinta fluxul de energie transportat prin unitatea de suprafata, in directie perpendiculara pe aceasta suprafata
7. Reflexia si refractia undelor elastice
Cand o unda intalnete suprafata de separare dintre doua medii diferite se produc simultan reflexia (intoarcerea undei in mediul din care a venit) si refractia (transmisia undei in mediul al doilea). Se constata de asemenea ca prin reflexie si refractie se schimba directia de propagare a undei.
Consideram o unda elastica longitudinala plana ce se propaga prin mediul (1), care are densitatea d1 si unde viteza undei este u1 (vezi fig.23). La intalnirea suprafetei de separare, dintre mediul (1) si mediul (2) unda se va imparti intr-o unda reflectata ce se propaga in mediul (1) si o unda transmisa ce se propaga in mediul (2).
Definim impedanta mediului de propagare prin produsul dintre densitatea mediului si viteza undei. Impedanta exprima viteza cu care se propaga energia undei prin mediul repectiv.
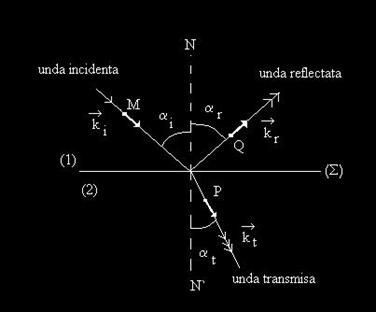
Fig. 2 Reflexia si refractia unei unde plane.
Observam ca amplitudinea undei transmise, At are acelai semn cu amplitudinea undei incidente, Ai, indiferent de impedantele celor doua medii. De aceea unda transmisa este totdeauna in faza cu unda incidenta.
In ceea ce privete amplitudinea undei reflectate se pot intalni doua cazuri:
a). Mediul (1) mai dens decat mediul (2), Z1>Z2. In acest caz amplitudinea undei reflectate, Ar, are acelai semn cu amplitudinea undei incidente, Ai. Cele doua unde sunt in faza, de asemenea.
b). Mediul (1) mai putin dens decat mediul (2), Z1<Z2. In acest caz amplitudinea undei reflectate, Ar, are semn opus fata de amplitudinea undei incidente, Ai. Cele doua unde sunt in opozitie de faza. Unda reflectata este defazata cu radiani in urma undei incidente.
Definim coeficientii de reflexie si de transmisie ai mediilor de propagare.
Coeficientul de reflexie este raportul dintre intensitatea undei reflectate si cea a undei incidente.
Coeficientul de transmisie este dintre intensitatea undei transmise si cea a undei incidente:
7.4. Unde stationare
Daca in mediul de propagare al undei se suprapun unda incidenta si unda reflectata, atunci se obtin unde stationare. Mai general, fenomenul de compunere a doua unde coerente se numeste interferenta. Compunerea undei incidente si a undei reflectate constituie un caz interesant de interferenta a undelor. Conform rezultatelor obtinute la reflexia undelor, se pot intalni doua cazuri, in functie de impedantele celor doua medii.
I. Daca mediul al doilea este mai putin dens decat primul, Z2<Z1, atunci unda reflectata este in faza cu unda incidenta. Sa consideram o unda liniara ce se propaga in mediul (1), pe o directie perpendiculara pe suprafata de separare dintre mediul (1)i mediul (2), ca in fig. 24. In punctul P se intalnesc unda incidenta si unda reflectata. Distanta dintre sursa undei si suprafata de separare dintre medii este l.
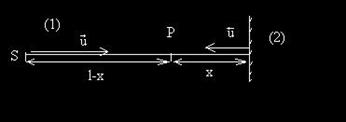
Fig. 24. Formarea undei stationare.
Fazele celor doua unde ce se intalnesc in punctul P depind de distantele (l-x) si reprectix (l+x) pe care le-a parcurs fiecare unda.
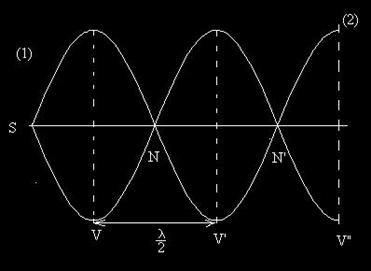
Fig. 25. Unda stationara obtinuta in cazul Z2<Z1.
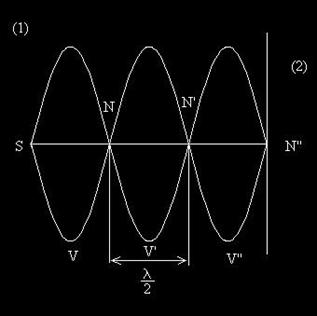
Fig. 26. Unda stationara obtinuta in cazul Z2>Z1.
7.5. Interferenta undelor
Fenomenul general de compunere a undelor coerente se numeste interferenta. Asa dupa cum stim, intensitatea undei reprezinta cantitatea de energie ce trece prin unitatea de suprafata in unitatea de timp.
Conditia de coerenta este ca diferenta
de faza dintre cele doua
unde, , sa fie independenta
de timp Aceasta conditie
este indeplinita de unde care au pulsatii egale si diferenta de faza
f (t)
Interferenta undelor longitudinale. Cu ajutorul a doua difuzoare plasate pe aceeai verticala si conectate la acelai amplificator se poate obtine un dispozitiv de inteferenta a undelor longitudinale, aa cum se vede in fig.26. Distanta dintre cele doua difuzoare (surse) este 2l. Presupunand ca ambele difuzoare emit simultan ele se comporta ca doua surse de unda, S1 si S2. De la ele se propaga doua unde coerente, care parcurg drumuri diferite pana in punctul P, aflat la distanta y de axa de simetrie (vezi fig. 27). In punctul P cele doua unde se suprapun si, fiind coerente, produc o figura de interferenta.
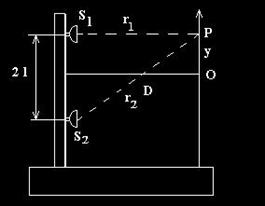
Fig. 27. Dispozitiv de interferenta a undelor longitudinale.
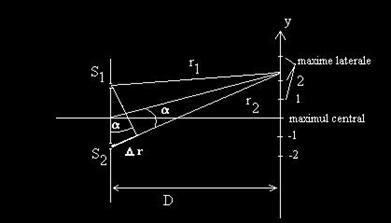
Fig. 28. Figura de interferenta obtinuta.
7.6. Difractia undelor
Consideram o unda plana care se propaga pe suprafata apei. Un obstacol de forma unui perete vertical cu o fanta de largime L se afla in calea undei, aa cum se vede in fig. 29.
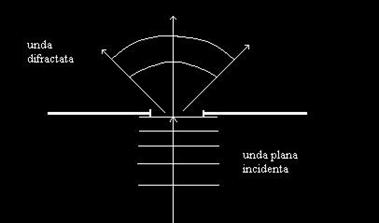
Fig. 29. Un obstacol pe care se produce difractia undei plane.
Se constata ca unda care trece dincolo de obstacolul intalnit are frontul de unda de forma sferica, dei unda incidenta avea fronturi de unda plane. Spunem ca unda a suferit fenomenul de difractie pe fanta de largime L.
Difractia este fenomenul de ocolire a obstacolelor de catre unde. Efectul difractiei este cu atat mai evident cu cat dimensiunea fantei (sau a obstacolului din calea undei) este de ordinul de marime al lungimii de unda a undei incidente.
In momentul cand frontul plan o atinge, fanta devine sediul unei infinitati de surse punctiforme infinitezimale, care genereaza la randul lor unde sferice in spatele fantei. Aceste unde se compun intre ele si formeaza o unda sferica ce se propaga in spatele obstacolului. Din punct de vedere fizic nu exista deosebiri intre difractie si interferenta. Ambele fenomene fizice presupun compunerea (adunarea) a doua sau mai multor unde coerente (difractia consta din interferenta unei infinitati de unde infinitezimale).
7.7. Polarizarea undelor elastice transversale
Consideram o unda elastica liniara transversala ce poate traversa spatiul dintre doi pereti verticali ce formeaza o fanta, asa cum se poate vedea in fig. 30. Am notat prin A i vectorul ce reprezinta amplitudinea oscilatiei din unda incidenta. Putem constata ca amplitudinea undei ce trece dincolo de fanta depinde de unghiul pe care-l formeaza vectorii A i cu directia fantei. Procesul prin care fanta filtreaza si lasa sa treaca numai componenta vectorului amplitudine care este in planul fantei constituie fenomenul de polarizare
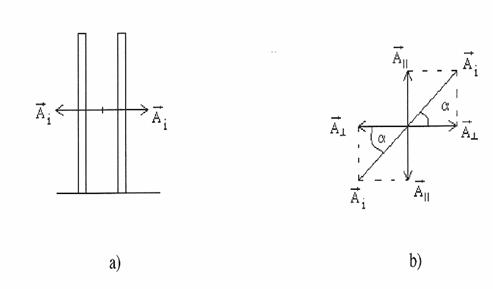
Fig. 30. Trecerea unei unde tarnsversale printr-o fanta.
a). vedere generala; b) directia de vibratie paralela cu fanta.
a) Daca amplitudinea undei este paralela cu fanta, unda se transmite prin fanta, iar unda transmisa are aceeai amplitudine ca cea incidenta (vezi fig. 30.b).
b) Daca directia de vibratie din unda incidenta este perpendiculara pe directia fantei, dincolo de fanta nu se mai propaga nici un fel de vibratie (vezi fig. 31.a).
c) Daca directia de vibratie face un anumit unghi cu fanta, atunci vectorul caracteristic al undei se decompune dupa doua directii perpendiculare, una din ele fiind directia fantei (vezi fig. 31.b).
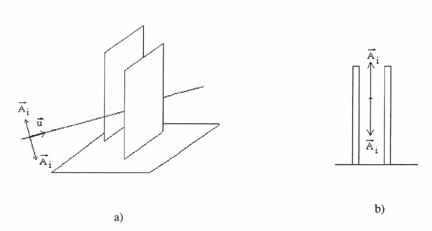
Fig. 31. Polarizarea la trecerea unei unde transversale printr-o fanta:
a) directia de vibratie este perpendiculara pe fanta;
b) descompunerea vectorului caracteristic pe doua directii.
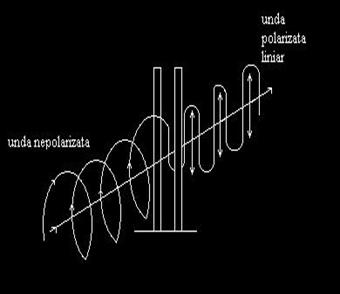
Polarizarea este fenomenul prin care se poate filtra dintr-o unda numai componenta intr-un anumit plan a vectorului de vibratie caracteristic undei. Dispozitivul prin care se realizeaza polarizarea se numete polarizor. Unda al carei vector de vibratie pastreaza aceeai directie in spatiu se numete unda liniar polarizata. In fig. 32.a) si b) se pot vedea doua exemple de unde liniar polarizate la ieirea din polarizor.
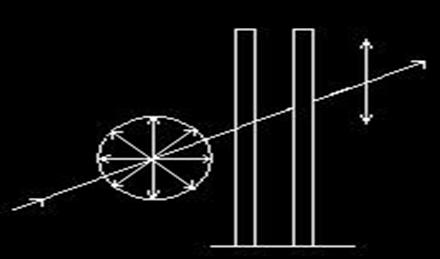
Mediile continue (gazele, lichidele, solidele) sunt medii de particule care interactioneaza intre ele si care, daca una din particule oscileaza, vor propaga oscilatia de la particula la particula sub forma de unde, numite unde elastice. Mediile de acest fel se numesc medii elastice.
Atunci cand oscilatiile in
fiecare punct sunt armonice de o anumita frecventa, ![]() (
(![]() -pulsatia), unda este o unda
monocromatica ce se propaga
fara atenuare.
-pulsatia), unda este o unda
monocromatica ce se propaga
fara atenuare.
![]() - elongatia
in cazul undei plane monocromatice care se propaga (fara
atenuare) pe directia axei Ox;
- elongatia
in cazul undei plane monocromatice care se propaga (fara
atenuare) pe directia axei Ox;
A0
- amplitudinea, care este
k - numar de unda, adica numarul de unde, de lungime de unda λ care se cuprind in 2π unitati de lungime.
Elongatia ψ este periodica in timp, cu perioada T, si periodica in spatiu (in raport cu coordonata x), cu perioada λ:
![]() ,
, ![]() ,
, ![]() ,
,
u -viteza de propagare a undei sau viteza de faza;
![]() - faza
undei care se propaga pe directia axei Ox;
- faza
undei care se propaga pe directia axei Ox;
Suprafetele de unda
sunt suprafete de faza
![]() -
ecuatia diferentiala a undelor care se propaga pe directia axei Ox;
-
ecuatia diferentiala a undelor care se propaga pe directia axei Ox;
![]() -
elongatia in cazul undei plane
monocromatice care se propaga in spatiu (fara atenuare) in
directia si sensul lui
-
elongatia in cazul undei plane
monocromatice care se propaga in spatiu (fara atenuare) in
directia si sensul lui ![]() ;
;
![]() -vector
de unda care are modulul
-vector
de unda care are modulul ![]() si este
orientat in directia si sensul de propagare a undei.
si este
orientat in directia si sensul de propagare a undei.
![]() -
elongatia in cazul undei sferice monocromatice;
-
elongatia in cazul undei sferice monocromatice;
Observatie: In cazul undei sferice amplitudinea de
oscilatie a punctelor mediului depinde de distanta fata de
sursa :![]() , unde A0 este
, unde A0 este
![]() - ecuatia
diferentiala a undelor care se propaga in spatiu,
- ecuatia
diferentiala a undelor care se propaga in spatiu,
![]() -
operatorul lui
-
operatorul lui
Intr-un mediu elastic se propaga, de-a
lungul axei Ox, undele longitudinale
descrise de legea: ![]() m. Sa se
determine:
m. Sa se
determine:
a) frecventa oscilatiilor punctelor mediului elastic;
b) viteza maxima de oscilatie a punctelor mediului elastic;
c) viteza de propagare a undei.
R: a) ν = 50 Hz, b) ![]() , vmax.=
0,3π m/s, c) u = 500π m/s.
, vmax.=
0,3π m/s, c) u = 500π m/s.
O unda plana ![]() m. Sa se
determine:
m. Sa se
determine:
a) raportul dintre amplitudinea de vibratie a particulelor mediului si lungimea de unda;
b) raportul dintre amplitudinea vitezei de vibratie a particulelor mediului si viteza de propagare a undei.
R: a) 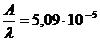 ; b)
; b)![]() .
.
O sursa de oscilatii armonice
oscileaza dupa legea: ![]() m. Pentru unda
plana care se propaga in lungul axei Ox, sa se determine
deplasarea fata de pozitia de echilibru a unui punct aflat la
distanta de x1 = 25
cm fata de sursa de oscilatii la t1 =0,04 s dupa inceperea oscilatiei. Viteza
cu care se propaga oscilatiile este de 250 m/s.
m. Pentru unda
plana care se propaga in lungul axei Ox, sa se determine
deplasarea fata de pozitia de echilibru a unui punct aflat la
distanta de x1 = 25
cm fata de sursa de oscilatii la t1 =0,04 s dupa inceperea oscilatiei. Viteza
cu care se propaga oscilatiile este de 250 m/s.
R: ![]() cm.
cm.
Sa se determine raportul amplitudinilor si defazajul dintre oscilatiile a doua puncte aflate la 10 m, respectiv 16 m fata de o sursa punctiforma de oscilatii, stiind ca perioada oscilatiilor este de 0,08 s, iar viteza de propagare a undei sferice este de 300 m/s.
R:![]() ;
; ![]() .
.
Sa se determine, in cazul undei plane, elongatia unui punct aflat la distanta de λ/4 fata de sursa de oscilatii pentru momentul T/ Amplitudinea oscilatiilor este de 7 cm.
R: 3,5 cm.
Pentru o unda plana, la momentul
T/3, distanta fata de pozitia de echilibru a unui punct
aflat la 5 cm fata de sursa de oscilatii este de ![]() din amplitudine.
Sa se determine lungimea de unda.
din amplitudine.
Sa se determine lungimea de unda.
R: 30 cm.
O
unda plana descrisa de legea ![]() , unde A, γ, ω si k sunt constante, se propaga
intr-un mediu omogen. Sa se calculeze defazajul
dintre punctele in care amplitudinile difera de n=2,5 ori, stiind γ
=0,458 m- 1 si λ
= 50 cm.
, unde A, γ, ω si k sunt constante, se propaga
intr-un mediu omogen. Sa se calculeze defazajul
dintre punctele in care amplitudinile difera de n=2,5 ori, stiind γ
=0,458 m- 1 si λ
= 50 cm.
R: ![]() .
.
O sursa punctiforma produce oscilatii sonore de frecventa ν=1,4 kHz. Unda sferica propagandu-se cu atenuare, la distanta r1 =3 m de la sursa amplitudinea de oscilatie a particulelor mediului este A1 = 30 μm, iar la distanta r2 = 8 m amplitudinea este de n = 4 ori mai mica. Sa se determine:
a) coeficientul γ de amortizare al undei;
b) viteza maxima de oscilatie a particulelor mediului la distanta r2.
Rezolvare:
a) ![]()
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]() m - 1;
m - 1;
b) 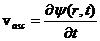
![]()
![]() ;
;
La
distanta r2 de sursa de
oscilatii ![]()
![]()
![]() m/s.
m/s.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4705
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved