| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Echivalenta propozitiilor
1. Definitie. Doua propozitii ![]() S(Q) se numesc echivalente
si scriem
S(Q) se numesc echivalente
si scriem ![]() daca pentru orice
valorizare v pe S(Q) avem
daca pentru orice
valorizare v pe S(Q) avem ![]() .
.
2. Propozitie. Doua propozitii ![]() S(Q) sunt echivalente daca si numai daca propozitia
S(Q) sunt echivalente daca si numai daca propozitia ![]() este tautologie.
este tautologie.
Demonstratie. Tabelul de
adevar al implicatiei prezentat in Sectiunea 4. arata
ca, pentru orice valorizare v
avem ![]() daca si
numai daca
daca si
numai daca ![]() ceea ce inseamna
ca
ceea ce inseamna
ca ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() .
.
3.
Corolar. Fie ![]()
![]() S(Q) astfel incat
S(Q) astfel incat![]() , n un numar intreg
pozitiv,
, n un numar intreg
pozitiv, ![]() S(Q) si
S(Q) si ![]() Q. Atunci
Q. Atunci ![]()
![]()
![]() .
.
Demonstratie. Conform lui 2., ![]() este tautologie si, conform Teoremei 3.8.,
este tautologie si, conform Teoremei 3.8., ![]() este de asemenea tautologie. Deoarece
este de asemenea tautologie. Deoarece ![]() =
= ![]()
![]() rezulta
rezulta ![]()
![]()
![]() .
.
4.Exemple. Din lista de tautologii prezentata la sfarsitul Sectiunii 4., rezulta, conform Propozitiei 2., urmatoarele echivalente:
![]() ( legea identitatii),
( legea identitatii), ![]() ( legea dublei negatii),
( legea dublei negatii), ![]() ( legea contrapozitiei),
( legea contrapozitiei), ![]() ( legea negarii implicatiei),
( legea negarii implicatiei),
![]() si
si![]() ( legile lui De Morgan).
( legile lui De Morgan).
Alte echivalente importante care sunt usor de demonstrat sau le vom demonstra in diverse exemple sau exercitii sunt:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
O metoda simpla de a
demonstra echivalenta a doua propozitii ![]() si
si ![]() este de a face
simultan tablele lor de adevar; cele doua propozitii sunt
echivalente daca si numai daca coloanele corespunzatoare
lui
este de a face
simultan tablele lor de adevar; cele doua propozitii sunt
echivalente daca si numai daca coloanele corespunzatoare
lui ![]() si
si ![]() in aceste table sunt
identice.
in aceste table sunt
identice.
Exemplu. Demonstram ca ![]() astfel:
astfel:
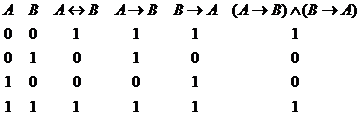
Echivalenta noastra rezulta din faptul ca coloanele 3 si 6 ale tablei de mai sus sunt identice.
6. Propozitie. Relatia ![]() pe multimea S(Q)
este o relatie de
echivalenta.
pe multimea S(Q)
este o relatie de
echivalenta.
Demonstratie. Fie ![]() S(Q). Deoarece
S(Q). Deoarece ![]() pentru orice
valorizare v avem
pentru orice
valorizare v avem ![]() . Presupunem
. Presupunem ![]() ; pentru orice valorizare v
avem
; pentru orice valorizare v
avem ![]() deci
deci ![]() ceea ce arata
ca
ceea ce arata
ca ![]() . In fine presupunem
. In fine presupunem ![]() si
si ![]() ; pentru orice valorizare v
avem
; pentru orice valorizare v
avem ![]() si
si ![]() deci
deci ![]() ceea ce arata
ca
ceea ce arata
ca ![]() . Astfel relatia
. Astfel relatia ![]() este reflexiva,
simetrica si tranzitiva adica este o relatie de
echivalenta.
este reflexiva,
simetrica si tranzitiva adica este o relatie de
echivalenta.
7. Lema. Fie
![]() S(Q)
astfel incat
S(Q)
astfel incat ![]() si
si ![]() . Avem, pentru orice
. Avem, pentru orice ![]() ,
, ![]() si
si ![]() .
.
Demonstratie. Pentru orice valorizare v
avem ![]() si rezulta,
evident,
si rezulta,
evident,
![]() ,
, ![]() .
.
8. Teorema. Fie ![]() S(Q)
astfel incat
S(Q)
astfel incat ![]() . Atunci
. Atunci ![]()
![]() .
.
Demonstratie. Vom aplica Teorema 2.10. pentru multimea de propozitii
P![]() S(Q)
S(Q)![]()
![]()
![]() }.
}.
Fie
![]() Q . Daca
Q . Daca ![]() avem
avem ![]() iar daca
iar daca ![]() avem
avem ![]() =A; in ambele
cazuri avem, evident,
=A; in ambele
cazuri avem, evident, ![]()
![]() deci
deci ![]() P. Astfel Q
P. Astfel Q![]() P.Acum fie
P.Acum fie ![]()
![]() P deci
P deci ![]()
![]() si
si ![]()
![]() . Avem, conform Lemei 7.,
. Avem, conform Lemei 7.,
![]()
![]() =
= ![]()
si
daca ![]() ,
,
![]()
![]()
![]()
![]()
![]() =
=![]()
asatfel
ca ![]() P. Conform Teoremei 2.10, avem P
P. Conform Teoremei 2.10, avem P![]() S(Q) ceea
ce demonstreaza afirmatia din enunt.
S(Q) ceea
ce demonstreaza afirmatia din enunt.
9. Exemplu. Demonstram
acum echivalenta ![]() cu ajutorul tablelor
de adevar:
cu ajutorul tablelor
de adevar:
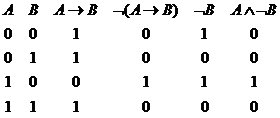
Echivalenta noastra rezulta din faptul ca coloanele 4 si 6 coincid.
10. Exemplu. Exemplificam acum modul in care se folosesc o parte din rezultatele precedentepentru a demonstra urmatoarea echivalenta:
![]()
![]() .
.
![]() in propozitia
in propozitia ![]() subpropozitia
subpropozitia ![]() se inlocuieste cu
se inlocuieste cu
![]() si deoarece,
conform lui , avem
si deoarece,
conform lui , avem ![]() rezulta, conform Teoremei
8,
rezulta, conform Teoremei
8,
(1) ![]()
![]()
![]() .
.
![]() conform lui 4, avem
conform lui 4, avem ![]() si, prin
inlocuirea lui A cu
si, prin
inlocuirea lui A cu ![]() si a lui B cu
si a lui B cu ![]() , rezulta, conform Corolarului 3,
, rezulta, conform Corolarului 3,
(2) ![]() .
.
![]() in propozitia
in propozitia ![]() se inlocuieste
subpropozitia
se inlocuieste
subpropozitia ![]() cu
cu ![]() si subpropozitia
si subpropozitia ![]() cu
cu ![]() ; deoarece, conform exemplului 9 avem
; deoarece, conform exemplului 9 avem ![]() si, evident,
si, evident,![]() rezulta:
rezulta:
(3) ![]()
![]() .
.
![]() avem, conform lui 4.,
avem, conform lui 4., ![]() si , conform
simetriei din Propozitie 6.,
si , conform
simetriei din Propozitie 6., ![]() ; prin inlocuirea lui A
cu
; prin inlocuirea lui A
cu![]() rezulta
rezulta ![]() si astfel:
si astfel:
(4) ![]()
![]() .
.
In final, aplicand tranzitivitatea din Propozitia 6., rezulta din (1),(2),(3) si (4):
![]()
![]() .
.
In continuare procedeul descris mai sus se va scrie pe scurt, fara referire la rezultatele teoretice folosite dar cu denumirea de metoda echivalentelor. In cazul nostru vom scrie:
![]()
![]()
![]()
![]()
![]()
![]() .
.
12. Exemplu. Vom demonstra legile lui De Morgan sub forma :
![]() si
si ![]() .
.
Pentru prima dintre ele folosim metoda tablelor de adevar:

Echivalenta
![]() rezulta din
faptul ca in tabela de mai sus coloanele 1 si 6 coincid. A doua lege a lui
De Morgan rezulta din prima folosind metoda echivalentelor din
Exemplul 10 :
rezulta din
faptul ca in tabela de mai sus coloanele 1 si 6 coincid. A doua lege a lui
De Morgan rezulta din prima folosind metoda echivalentelor din
Exemplul 10 :
![]() .
.
(
am folosit legea dublei negatii: ![]() si prima lege a
lui De Morgan de mai sus).
si prima lege a
lui De Morgan de mai sus).
12. Definitie. Fie ![]() o propozitie in a
carei expresie apar numai conectorii
o propozitie in a
carei expresie apar numai conectorii ![]() . Propozitia
. Propozitia ![]() care se obtine
din
care se obtine
din ![]() prin inlocuirea
fiecarei aparitii a lui
prin inlocuirea
fiecarei aparitii a lui ![]() cu
cu![]() si a fiecarei aparitii a lui
si a fiecarei aparitii a lui ![]() cu
cu ![]() se numeste duala propozitiei
se numeste duala propozitiei ![]() . Astfel daca
. Astfel daca ![]() atunci duala lui
atunci duala lui ![]() este propozitia
este propozitia ![]() . Evident, pentru orice propozitie
. Evident, pentru orice propozitie ![]() , avem
, avem ![]() .
.
13.
Teorema( Teorema de dualitate). Pentru orice doua propozitii ![]() avem:
avem:
(i)
![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() este tautologie;
este tautologie;
(ii)
![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() este tautologie;
este tautologie;
(iii)
daca ![]() atunci
atunci ![]() .
.
Demonstratie. (i) Daca ![]() este tautologie atunci,
conform Corolarului 3., propozitia
este tautologie atunci,
conform Corolarului 3., propozitia ![]() care se obtine
din
care se obtine
din ![]() prin inlocuirea
fiecarui atom A care apare in
expresia lui
prin inlocuirea
fiecarui atom A care apare in
expresia lui ![]() cu negatia sa
cu negatia sa ![]() este de asemenea o
tautologie. Pe de alta parte din legile lui De Morgan rezulta,
evident,
este de asemenea o
tautologie. Pe de alta parte din legile lui De Morgan rezulta,
evident, ![]() astfel ca
astfel ca ![]() este de asemenea
tautologie. Pentru a demonstra afirmatia reciporoca, notam
este de asemenea
tautologie. Pentru a demonstra afirmatia reciporoca, notam ![]() si observam
ca
si observam
ca ![]() deci
deci ![]() . Astfel daca presupunem ca
. Astfel daca presupunem ca ![]() este tautologie
rezulta, din cele de mai sus ca
este tautologie
rezulta, din cele de mai sus ca ![]() si deci
si deci ![]() este tautologie.
este tautologie.
(ii)
Avem, evident, ![]() si rezulta,
conform Corolarului 3,
si rezulta,
conform Corolarului 3, ![]() . Astfel, conform lui (i),
. Astfel, conform lui (i), ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() este tautologie. Pe de alta parte avem:
este tautologie. Pe de alta parte avem:
![]()
![]()
![]()
![]()
si afirmatia din enunt este evidenta.
(iii) Evident, ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() si
si ![]() sunt tautologii.
Deoarece
sunt tautologii.
Deoarece ![]() rezulta ca
rezulta ca ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() si
si ![]() sunt tautologii adica,
conform lui (ii), daca si numai daca
sunt tautologii adica,
conform lui (ii), daca si numai daca ![]() este tautologie.
Astfel
este tautologie.
Astfel ![]() este tautologie
daca si numai daca
este tautologie
daca si numai daca ![]() este tautologie.
Afirmatia rezulta acum din Propozitia 2.
este tautologie.
Afirmatia rezulta acum din Propozitia 2.
14. Exemplu. Vom demonstra echivalentele:
![]() ,
, ![]() .
.
Prima rezulta din tablele de adevar de mai jos:
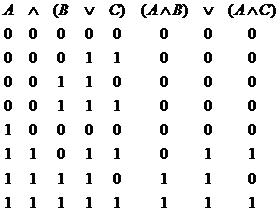
Pentru
a doua procedam astfel: daca notam ![]()
![]()
![]() si
si ![]()
![]() avem
avem ![]()
![]() si
si ![]()
![]() ; conform echivalentei precedente avem
; conform echivalentei precedente avem![]() si, conform Teoremei 13., rezulta
si, conform Teoremei 13., rezulta ![]() adica exact cea de a doua ecivalenta. Spunem
ca a doua echivalenta rezullta din prima prin dualitate.
adica exact cea de a doua ecivalenta. Spunem
ca a doua echivalenta rezullta din prima prin dualitate.
Exercitii
Fie ![]() S(Q). Aratati
ca:
S(Q). Aratati
ca:
a) Daca
![]() este tautologie atunci
este tautologie atunci
![]() si
si ![]() .
.
b) Daca
![]() este contradictie
atunci
este contradictie
atunci ![]() si
si ![]() .
.
c) Daca ![]() este tautologie atunci
este tautologie atunci
![]() .
.
2. Demonstrati urmatoarele echivalente (folosind diverse metode prezentate anterior):
a) ![]() , b)
, b) ![]() ,
,
c) ![]() , d)
, d) ![]() ,
,
e)![]()
![]()
f)
![]() , g)
, g) ![]() , h)
, h) ![]() ,
,
i) ![]() , j)
, j) ![]() .
.
3. Aratati ca
![]() .
.
4. Fie ![]() o propozitie.
Demonstrati ca:
o propozitie.
Demonstrati ca:
a) daca in expresia lui ![]() apare numai conectorul
apare numai conectorul
![]() atunci
atunci ![]() este tautologie daca si numai daca fiecare
atom A
este tautologie daca si numai daca fiecare
atom A![]() Q apare in
expresia lui
Q apare in
expresia lui ![]() de un numar par
de ori;
de un numar par
de ori;
b) daca in expresia lui ![]() apar numai conectorii
apar numai conectorii ![]() si
si ![]() atunci
atunci ![]() este tautologie daca si numai daca fiecare
atom A
este tautologie daca si numai daca fiecare
atom A![]() Q precum si conectorul
Q precum si conectorul ![]() apar in expresia lui
apar in expresia lui ![]() de un numar par
de ori.
de un numar par
de ori.
Rezolvari
1. Fie v o valorizare oarecare.
(a)
Deoarece ![]() este tautologie avem
este tautologie avem ![]() si rezulta:
si rezulta:
![]() ,
,
![]() .
.
(b) Deoarece ![]() este contradictie
avem
este contradictie
avem ![]() si rezulta:
si rezulta:
![]() ,
,
![]() .
.
(c) Deoarece ![]() este tautologie avem
este tautologie avem ![]() si rezulta:
si rezulta:
![]() .
.
![]()
![]()
![]()
![]()
![]() .
.
b) Avem:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
c) Rezulta din b) prin dualitate.
d) Avem:
![]() .
.
e) Folosim Exemplu 1 si b) de si avem:
![]()
![]()
![]()
![]() .
.
f) Folosim e) si avem:
![]()
![]()
![]()
![]() .
.
g) Tablele de adevar sunt:
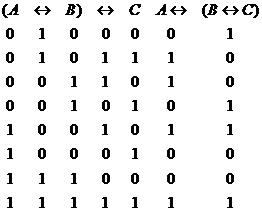
h) Rezulta din tabla de adevar de mai jos
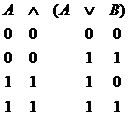
i) Rezulta din h) prin dualitate.
j) Rezulta din tabla de adevar de mai jos:
![]()
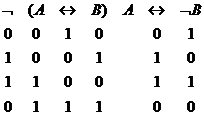
3. Pentru mai multa claritate preferam ca propozitiile sa fie scrise sub forma completa( dar fara parantezele exterioare) si deci avem de aratat ca
![]() .
.
Avem:
![]()
![]()
![]()
![]() .
.
4.
a) Din ![]() unde n este un numar intreg pozitiv
si, pentru fiecare
unde n este un numar intreg pozitiv
si, pentru fiecare ![]() ,
, ![]() care contine
numai conectorul
care contine
numai conectorul ![]() si toti
atomii sai coincid sa zicem cu
si toti
atomii sai coincid sa zicem cu ![]()
![]() Q; evident, putem
presupune ca atomii
Q; evident, putem
presupune ca atomii ![]() sunt distincti.
Deoarece
sunt distincti.
Deoarece ![]() este tautologie
rezulta ca, pentru fiecare
este tautologie
rezulta ca, pentru fiecare ![]() , daca notam
cu
, daca notam
cu ![]() numarul de atomi ai lui
numarul de atomi ai lui ![]() atunci
atunci ![]() este tautologie in
cazul cand
este tautologie in
cazul cand ![]() este par iar in cazul
este par iar in cazul ![]() impar avem
impar avem ![]() ( vezi si 1.c)). Rezulta, in particular, ca
daca
( vezi si 1.c)). Rezulta, in particular, ca
daca ![]() este par pentru orice
este par pentru orice ![]() atunci
atunci ![]() este tautologie. In
caz contrar avem
este tautologie. In
caz contrar avem
![]()
unde
s este un numar intreg pozitiv
si ![]() sunt atomi
distincti; in aceasta situatie putem considera o valorizare v astfel incat
sunt atomi
distincti; in aceasta situatie putem considera o valorizare v astfel incat ![]() si
si ![]()
![]() si avem, evident,
si avem, evident, ![]() .
.
b) Folosim ![]() . Rezulta
. Rezulta
![]()
![]()
unde
n este un numar intreg pozitiv
si, pentru fiecare ![]() ,
, ![]() este o propozitie
a carei expresie contine numai conectorii
este o propozitie
a carei expresie contine numai conectorii ![]() si
si ![]() si acelasi
atom sa zicem
si acelasi
atom sa zicem ![]() ; in plus atomii
; in plus atomii ![]() sunt distincti
si numarul aparitiilor conectorului
sunt distincti
si numarul aparitiilor conectorului ![]() in expresia lui
in expresia lui ![]() are aceiasi
paritate cu numarul aparitiilor sale in expresia lui
are aceiasi
paritate cu numarul aparitiilor sale in expresia lui ![]() . Putem presupune
. Putem presupune ![]()
![]() . Pentru fiecare
. Pentru fiecare ![]() fie
fie ![]() numarul
aparitiilor atomului
numarul
aparitiilor atomului ![]() in expresia lui
in expresia lui ![]() , egal cu numarul aparitiilor lui
, egal cu numarul aparitiilor lui ![]() in expresia lui
in expresia lui ![]() , si
, si ![]() numarul
aparitiilor conectorului
numarul
aparitiilor conectorului ![]() in expresia lui
in expresia lui ![]() . Avem
. Avem
![]() ,
,
![]() si
si ![]() Q. Avand in vedere ca
Q. Avand in vedere ca ![]() este tautologie
rezulta ca: daca
este tautologie
rezulta ca: daca ![]() si
si ![]() sunt pare atunci
sunt pare atunci ![]() este tautologie;
daca
este tautologie;
daca ![]() este impar si
este impar si ![]() este par atunci
este par atunci ![]() , daca
, daca ![]() este par si
este par si ![]() este impar atunci
este impar atunci ![]() iar daca
iar daca ![]() si
si ![]() sunt impare atunci
sunt impare atunci ![]() este o
contradictie. Fie
este o
contradictie. Fie ![]() numarul indicilor
numarul indicilor
![]() astfel ca
astfel ca ![]() si
si ![]() sunt impare,
sunt impare, ![]() numarul indicilor
numarul indicilor
![]() astfel ca
astfel ca ![]() par si
par si ![]() impar sau
impar sau ![]() impar si
impar si ![]() par,
par, ![]() numarul indicilor
numarul indicilor
![]() astfel ca
astfel ca ![]() si
si ![]() sunt impare. Rezulta
ca
sunt impare. Rezulta
ca ![]() este tautologie
daca si numai daca, pentru orice
este tautologie
daca si numai daca, pentru orice ![]() ,
, ![]() si
si ![]() par, echivalent,
daca si numai daca pentru orice
par, echivalent,
daca si numai daca pentru orice ![]() ,
, ![]() este par si
este par si ![]() este par.
este par.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3077
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved