| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CALCUL DIFERENTIAL PENTRU FUNCTII DE n VARIABILE REALE
Obiective : insusirea de catre studenti a rolului derivatelor partiale de ordin unu si doi in studiul
functiei reale de n variabile reale si mai ales a gasirii extremelor libere sau cu legaturi ale
functiei , direct sau cu computerul .
Cuprins :
Rolul derivatelor partiale de ordinul unu si doi in studiul functiilor de n variabile reale
Extreme libere ale functiilor de n variabile reale
Extreme cu legaturi ale functiilor de n variabile reale
Metoda Newton-Raphson pentru rezolvarea sistemelor neliniare
Rezumat
Intrebari
Bibliografie
Cuvinte-cheie : functie reala de n variabile reale , derivate partiale de ordinul unu si doi ,
maximele si minimele libere sau conditionate ale unei functii , metode iterative de rezolvare
a unui sistem neliniar de ecuatii .
1 Rolul derivatelor partiale de ordinul unu si doi in studiul functiilor de n variablile
reale
Fie multimea de vectori A Rn si multimea de scalari B R .
Se spune ca s-a definit o functie reala de n variabile reale daca oricarui vector X I A ii corespunde numarul real unic y = f (X)I B .
Daca X = (x1,.,xn) , functia f se va scrie : y = f (x1,.,xn) .
Un sistem de m functii reale de n variabile reale este multimea de functii :
y1 = f1 (x1,.,xn)
........
ym = fm (x1,.,xn)
definite pe A Rn cu valori in B R .
Un asemenea sistem de functii reale este in fond o functie o functie vectoriala de variabila vectoriala , definita pe Rn cu valori in Rm , care asociaza vectorului
X = (x1,.,xn) I A Rn un vector unic Y = (y1,.,ym) I B Rm .
Asemenea functii sunt operatorii liniari definiti pe Rn cu valori in Rm .
Caz particular
Pentru n = 2 functia y = f(x1,x2) reprezinta o suprafata in spatiul R3 iar sistemul de functii
y = f 1(x1,x2) ; y = f2 (x1,x2) reprezinta o intersectie de suprafete in R3 deci o curba spatiala in R3 .
De exemplu functia y = b0 + b1 x1 + b2 x2 reprezinta un plan in spatiul R3 iar sistemul de functii y = b0 + b1 x1 + b2 x2 ; y = c0 + c1 x1 + c2 x2 reprezinta fie o dreapta in spatiul R3 fie o pereche de plane paralele in R3 .
Functia y = b0 + b1x1+b2x2 + c1x12 + c2x1x2 + c3x22 reprezinta deasemenea o suprafata in spatiul R3 .
O functie reala de n variabile reale y = f (x1,.,xn) se numeste functie de productie daca x1,.,xn sunt factori(resurse) pentru cultura plantelor sau cresterea animaloelor iar y este productie fizica sau valorica in agricultura .
Unei functii reale de n variabile y = f (x1,.,xn) i se asociaza functiile ajutatoare :
a) Functiile partiale de o variabila reala :
y = f ( x10 ,., xi - 1 ,0 , xi ,xi+1,0 , . , xn 0 ) = fi (xi)
Aici doar xi este variabila , restul argumentelor fiind constante .
Graficele functiilor partiale pentru diferite valori concrete ale variabilelor , se numesc izocuante .
b) Functia izovalorica
y0 = f (x1,.,xn)
Aici este fixata valoarea y deci cunoscand valorile a n - 1 dintre variabilele xi ,se poate calcula valoarea celei de a n-a variabile , astfel ca y = y0 .
Graficele functiilor izovalorice pentru diferite valori concrete ale lui y , se numesc curbe izovalorice .
Fie functia reala y = f (x1,.,xn) , f : A Rn R si fie vectorul fixat x(0) = ( x10 ,., xn0 ) I A .
Limita functiei f in punctul x(0) este numarul unic si finit L astfel ca pentru orice e > 0 exista
d e) > 0 astfel ca pentru orice x =
(x1,.,xn) I A cu x - x(0) < e rezulta ![]()
f(x) - L < e . Daca in plus :
se spune ca functia f este continua in x(0) in raport cu ansamblul variabilelor x1,.,xn
In acest caz functiile partiale y = fi (xi ) sunt si ele continue in raport cu variabilele lor.
Functia reala y = f (x1,.,xn) este diferentiabila in x(0) I A daca exista constantele
C1,.,Cn astfel ca pentru orice x I A cu x - x(0) < e , avem :
f (x1,.,xn) = f (x10,.,xn0) + C1.(x1 - x10 )+.+Cn.(xn- xn0 ) + e(x1,.,xn). x - x(0)
unde e(x1,.,xn) 0 pentru x x(0) .
Functia reala y = f (x1,.,xn) are derivate partiale in x(0) I A daca functiile partiale
![]()
y = fi (xi) sunt derivabile
in xi 0 si au derivatele :
Daca f este diferentiabila in x(0) I A , atunci f are derivate partiale in x(0) I A .
Daca finctia f are derivate partiale continue in x(0) I A , atunci ea este diferentiabila in
x(0) I A .Vectorul :
![]()
se numeste gradientul
functiei f in x(0) .
Diferentiala de ordinul intai a lui f in x(0) este polinomul omogen cu variabilele
![]()
dx1,.,dxn :
El este produsul scalar intre vectorul Grad f (x(0)) si vectorul-deplasare dx = (dx1,.,dxn)
Derivatele partiale ale lui y = f (x1,.,xn) sunt si ele functii reale de n variabile reale :
![]()
Daca aceste derivate au la randul
lor derivate partiale in raport cu x1,.,xn , se spune ca
functia f are derivate partiale de ordinul doi
![]()
Daca derivatele partiale de
ordinul doi sunt continue atunci derivatele mixte sunt egale :
![]()
Derivatele partiale de ordinul doi
ale lui f formeaza in punctul x(0) = (x10,.,xn 0)
I A
o matrice numerica numita matricea Hessiana a lui f :
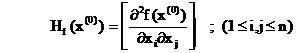
Diferentiala de ordin doi a
lui f este polinomul omogen de grad doi in
variabilele
dx1,.,dxn :
![]()
unde dx = (dx1,.,dxn) este vectorul-deplasare iar (dx)T
este transpusul sau .
Diferentiala de ordinul doi a lui f se numeste pozitiv-definita daca pentru orice vector-deplasare dxIRn , avem : d2f (x(0)) = (dx).Hf(x(0)).(dx)T > 0 .
Cu notatiile :
![]()
conform criteriului lui Sylvester
, d 2 f (x(0)) este pozitiv-definita daca Hf(x(0))
este matrice pozitiv-definita adica daca :
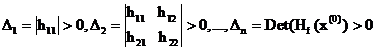
adica toti minorii
principali sunt strict pozitivi in x(0)
.
Diferentiala de ordinul doi a lui f se numeste negativ-definita daca pentru orice vector-deplasare dxIRn , avem : d2f (x(0)) = (dx).Hf(x(0)).(dx)T < 0 .
Conform criteriului lui Sylvester , d 2 f (x(0)) este negativ-definita daca Hf(x(0)) este matrice negativ-definita adica daca :
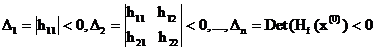
adica toti minorii
principali sunt strict negativi in x(0)
.
2 Extreme libere ale functiilor de n variabile reale
Functia reala de n variabile reale y = f (x1,.,xn),f:A Rn B R are in x(0) = ( x10 ,., xn0 )IA un maxim relativ daca pentru orice x I A cu x - x(0) < e avem f(x) < f(x(0)) deci in sfera cu centrul x(0) si raza e , valoarea f(x(0)) este cea mai mare .
Functia reala de n variabile reale y = f (x1,.,xn) are in x(0) = ( x10 ,., xn0 ) I A un minim relativ daca pentru orice x I A cu x - x(0) < e avem f(x) > f(x(0)) deci in sfera cu centrul x(0) si raza e , valoarea f(x(0)) este cea mai mica .
Daca functia f are cel putin un maxim relativ, cel mai mare maxim relativ se numeste
maxim absolut pentru functia f .
Daca functia f are cel putin un minim relativ, cel mai mic minim relativ se numeste
minim absolut pentru functia f .
Daca functia f are un minim absolut si un maxim absolut , ea se numeste marginita .
Fie functia reala de n variabile reale y = f (x1,.,xn) , f: A Rn B R si fie
x(0) = ( x10 ,., xn0 ) I A .
Daca f are derivate partiale continue de ordinul doi in sfera
(deci este diferentiabila in aceasta sfera ) atunci pentru orice x = (x1,.,xn) in sfera
precedenta avem formula Taylor :
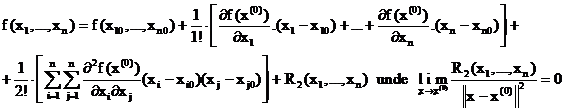
Pentru functii reale de n variabile reale are loc o teorema asemanatorare cu teorema 7.3
si anume :
Daca functia f are derivate partiale continue in sfera si x(0)
este un punct de maxim sau de minim relativ , avem :
![]()
Demonstratie
Fie de exemplu x(0) = ( x10 ,., xn0 ) I A punct de maxim relativ pentru f deci x10
este punct de maxim relativ pentru functia partiala y = f1(x1) = f(x1,x20,.,xn0) deci
conform teoremei 7.3 avem f (x(0) ) / x1 = 0 . Rationamentul este analog pentru
variabilele x2,.,xn . Q.E.D.
Punctele x(0) I A Rn cu f (x(0) ) / x1 = 0,., f (x(0) ) / xn = 0 , se numesc puncte
stationare ale functiei f pentru ca in aceste puncte planul tangent la graficul functiei f
este orizontal ( valorile functiei f stationeaza in x avand viteza de variatie Gradf (x(0)
nula ). In punctele stationare x(0 vectorii Gradf (x(0) ;I dx = (dx1,.,dxn) sunt ortogonali .
Conditia din teorema 1 este necesara dar nu suficienta peunrt puncte de maxim sau de minim relativ , adica nu orice punct stationar este punct de maxim sau de minim relativ .
O conditie suficienta de maxim sau de minim relativ este data de :
Teorema 2
Fie functia reala de n variabile reale y = f (x1,.,xn) cu derivate partiale de ordinul doi continue in sfera unde x(0) I A este punct stationar pentru functia f adica
f (x(0) ) / xi = 0 ; (i=1,.,n) .
Daca matricea hessiana Hf (x(0)) este pozitiv-definita , atunci x(0) este punct de maxim relativ pentru f .
Daca matricea hessiana Hf (x(0)) este negativ-definita , atunci x(0) este punct de minim relativ pentru f .
In celelalte cazuri x(0) nu este punct de extrem relativ pentru f .
Demonstratie
Daca x(0) este punct stationar pentru functia f , formula Taylor de mai sus , se scrie :
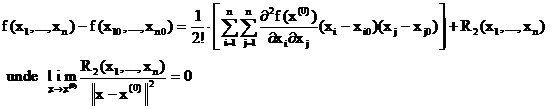
Notand r x - x(0) , din aceasta relatie avem :
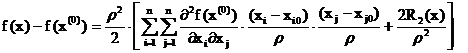
Fie sfera-unitate S = .
Avem ((x1-x10) / r ,., (xn - xn0 ) / r I S .
Pentru r suficient de mic , termenul R2(x) / (r ) se poate neglija deci f(x) - f(x(0))
are acelasi semn cu :
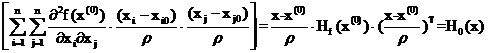
Daca Hf(x(0)) este pozitiv-definita , pentru orice x cu x - x(0) < e avem H0(x)>0
deci f(x) > f(x(0)) adica x(0) este punct de minim relativ pentru f .
Daca Hf(x(0)) este negativ-definita , pentru orice x cu x - x(0) < e avem H0(x)<0
deci f(x) < f(x(0)) adica x(0) este punct de maxim relativ pentru f .
In restul cazurilor, pentru unii vectori x cu x - x(0) < e avem f(x) > f(x(0)) iar pentru
alti vectori x cu x - x(0) < e avem f(x) < f(x(0)) deci x(0) nu este punct de extrem relativ
ci punct-sa . Q.E.D.
Exemplu
Sa se afle extremele functiei y = - 4 x13 - 9 x23 - x33 +12x1 + 27x2+12x3
Solutie
a) Anulam derivatele partiale de ordinul unu ale functiei f pentru a gasi punctele ei stationare :
y / x1 = - 12 x12+12 = 0
y / x2 = - 27 x22+27 = 0
y / x3 = - 3 x12+12 = 0
Sistemul are 8 solutii de forma ( x10= 1 , x20 = 1 , x30 = 2) adica 8 puncte stationare .
b) Derivam partial in raport cu x1,x2,x3 fiecare derivata partiala de ordinul unu de la punctul a) si obtinem Hessiana :
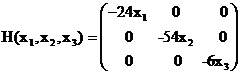
Avem minorii principali : Δ1
= - 24x1 ; Δ2
= 1296x1x2 ; Δ3 = - 7776x1x2x3 .
Numai pentru punctul stationar M1(1,-1,2) avem Δ1 <0 ; Δ2 >0 ; Δ3 <0 deci M1 este singurul punct de maxim relativ pentru f .
Numai pentru punctul stationar M2(-1,1,-2) avem Δ1 >0 ; Δ2 >0 ; Δ3 >0 deci M2 este singurul punct de minim relativ pentru f .
Celelalte 6 puncte stationare nu sunt puncte de extrem relativ pentru f .
Aplicatii
Dreapta de regresie in statistica
Fie in planul R2 punctele M1(x1,y1),., Mn(xn,yn) . Se cere ecuatia dreptei y=B0+B1.x pentru care functia de doua variabile este minima : f(B0,B1)= (y1-B0-B1.x1)2+.+ (yn-B0-B1.xn)2 = minim
(Metoda celor mai mici patrate)
Solutie
Aflam punctele stationare ale functiei f , anuland derivatele partiale de ordinul unu
ale lui f in raport cu B1,B0 :
∂ f / ∂B1 = 2(y1-B0 - B1x1).(-x1)+.+ 2(yn-B0 - B1xn).(-xn) = 0
∂ f / ∂B0 = 2(y1-B0 - B1x1).(-1) + . +2(y1-B0 - B1x1).(-1) = 0
Acest sistem liniar se numeste sistem de ecuatii normale si are forma :
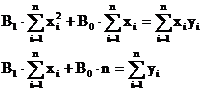
cu solutia (punctul stationar) :
Derivatele partiale de
ordinul doi ale functiei f sunt :
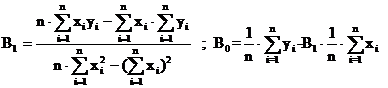
![]()
Matricea hessiana este :
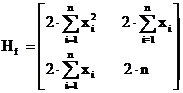
Avem in punctul stationar :
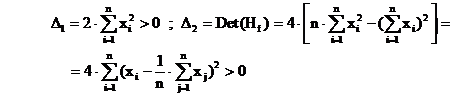
deci avem un punct de minim .
B1 se numeste coeficient de regresie liniara iar B0 se numeste termen liber al regresiei .
Stocuri optime cu cerere constanta
Un stoc este o acumulare de bunuri materiale care urmeaza sa fie folosite in productie sau valorificate in consum .
Intensitatea aprovizionarii cu bunuri materiale nu poate fi totdeauna egala cu intensitatea cererii acestor bunuri pentru productie / consum deci se impune necesitatea stocarii lor .
Exemple de stocuri in agricultura
Stocuri de produse agricole vegetale in silozuri ;
Stocuri de produse zootehnice in depozite ;
Stocuri de ingrasaminte,insecticide ,ierbicide la furnizori ;
Stocuri de carburanti si piese de schimb in atelierele mecanice ;
Stocuri de seminte pentru semanat la unitatile producatoare de seminte ;
Stocuri de material seminal pentru insamantari artificiale la animale la unitatile de de profil ;
Stocarea bunurilor materiale , numite conventional si articole , presupune comandarea si transportarea lor in stoc cu costul de aprovizionare ca (lei / serie) ; aceste bunuri materiale sunt imobilizate in stoc, lipsind din procesul de productie / consum si trebuind ferite de depreciere sau sustragere , deci ele comporta un cost de stocare cs (lei / articol.unitate de timp ).
Daca intensitatea cererii pentru productie / consum de articole , depaseste intensitatea stocarii acestora , numarul de articole din stoc poate deveni zero , creindu-se penurie de articole cu costul de penurie cp (lei / articol.unitate de timp ) .
A. Stocuri cu aprovizionare instantanee
Cu privire la modul de aprovizionare cu articole , vom presupune ca aprovizionarea se face instantaneu cu un numar r de articole , r fiind acelasi pentru perioade de timp egale , de lungime t intre doua aprovizionari consecutive adica stocurile sunt cu cerere constanta .
Fie perioada de timp totala de lungime T pentru care exista cererea totala de N articole .
In prima perioada de timp de lungime t se aduc in stoc r = m articole fata de n articole planificate (m ≤ n ) ; aceste m articole consumandu-se in procesul de productie / consum , in urmatoarea perioada de timp de lungime t se aduc alte m articole , etc.
La sfarsitul perioadei de timp totale de lungime T , cererea totala de N articole este integral satisfacuta iar volumul stocului este zero .
Datorita conditiei m ≤ n , rezulta ca exista subperioade de timp de lungime t - u la sfarsitul perioadelor de timp de lungime t , in care volumul stocului ajunge zero (penurie de n - m articole) deci apare costul de penurie cp (lei / articol.unitate de timp ).
In ipoteza consumului liniar de articole din stoc , volumul stocului evolueaza astfel : in subperioadele de timp [ it ; it+u] stocul scade de la m articole la zero articole iar pe subperioadele de timp [ it +u ; (i+1)t] exista penurie de n - m articole , urmata de o noua aprovizionare cu m articole (i = 0,1,.,k-1) . Aici k este numarul de aprovizionari in serii de cate m articole .
Intensitatea stocarii planificate este m = (n / t) articole / unitate de timp iar a celei realizate este
m = (m / u) articole / unitate de timp .
Intensitatea cererii este λ = (N / T ) articole / unitate de timp .
Vom presupune ca m m = λ adica n / t = m / u = N / T si ca avem k aprovizionari in serii de cate m articole in subintervale de timp de lungime u , asa ca vom avea :
k = T / t = N / n ; T / u = N / m
Costul aprovizionarii cu o serie de m articole este ca (lei / serie), costul stocarii acestei serii este
(m / 2).u.cs unde m / 2 este volumul mediu de articole stocate pe perioada de timp de lungime u iar costul penuriei a n - m articole este ((n-m) / 2). (t-u).cp unde (n - m) / 2 este numarul mediu de articole care lipsesc din stoc pe subperioada de timp de lungime t - u de la sfarsitul perioadei de timp de lungime t .
Costul total al aprovizionarii, stocarii si penuriei pentru cele N articole necesare in perioada de timp totala de lungime T , va fi :
![]()
Dar k = N / n ; u = m.(T / N ) si t - u = (n-m).( T / N ) asa ca vom minimiza functia de variabilele n , m a costului total de aprovizionare , stocare si penurie :
![]()
Derivam partial in raport cu n si m :
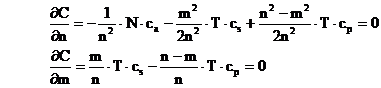
Cu notatia ρ = cp / (cs+cp ) deci 0< ρ < 1 acest sistem are solutia (punctul stationar) :
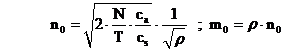
Se verifica conditiile :
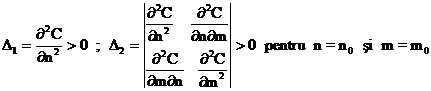
deci in adevar avem un minim .
Valoarea minimului este C(n0 , m0) = T.cs.m0
Numarul optim de aprovizionari cu n0 articole planificate va fi : k0 = N / n0 .
Lungimea optima a intervalelor de timp intre doua aprovizionari va fi : t0 = T / k0
Durata optima a subperioadelor de timp fara penurie va fi : u0 = ρ.t0 .
Daca cs este neglijabil in raport cu cp , avem ρ → 1 deci m0 → n0 si penuria dispare (stocurile sunt cu articole suficiente ) .
In acest caz avem :
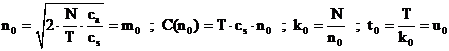
Exemplu
La o ferma zootehnica , necesarul anual de furaje concentrate este de N = 200 tone
pentru T = 365 zile . Costul de aprovizionare este ca = 100 lei / serie iar cel de stocare este
cs = 5 lei / tona.zi .
Absenta furajelor concentrate duce la cheltuieli suplimentare astfel ca costul de penurie este
cp = 3.5 lei / tona.zi .
Se cer valorile optime n0 , m0 , C(n0 , m0) , k0 , t0 , u0 .
Solutie
Avem ρ = cp / (cs + cp ) = 0.875 . Rezulta :
n 0 = [(2.N.ca) / (T.cs ) . (1 / ρ1 / 2 ) = 15.83 tone planificate pe serie .
m0 = ρ.no = 13.85 tone realizate pe serie.
C(n0 , m0 ) = T.cs.m0 = 2527.625 lei .
k 0 = N / n0 = 12.63 serii .
t0 = T / k0 = 29 zile intre doua aprovozionari succesive .
u0 = ρ.t0 = 25.29 zile fara penurie .
B. Stocuri optime cu aprovizionare treptata
Intensitatea ofertei este de m articole / unitete de timp iar intensitatea cererii este de l articole / unitate de timp. Presupunem ca m > l pentru a putea constitui stocul . Fie r = cp / ( cs + cp ) I
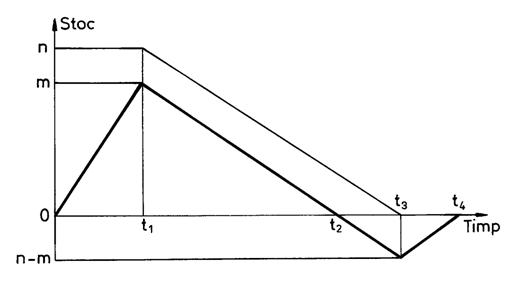
Avem t1 = s ; t2 = s + u ; t3 = s + u + t ; t4 = s + u + t + r .
In intervalul de timp 0 ; t1 de lungime s , se ofera m s articole si se cer l s articole deci stocul contine (m l )s articole .
In intervalul de timp t1 ; t2 de lungime u se consuma in totalitate stocul de (m l )s articole deci :
m l )s = l u
In intervalul de timp t2 ; t3 de lungime t se creeaza deficitul de stoc de lt articole .
In intervalul de timp t3 ; t4 de lungime r se reia oferta de m r articole si se cer l r articole pina la lichidarea deficitului de stoc asa ca :
l t = (m l ) r
Cheltuielile pe intervalul total de timp 0 ; t4 de lungime r + t + u + s sunt formate din :
a) Cheltuieli de lansare a productiei ca (lei) ;
b) Cheltuieli medii de stocare egale cu cs . (m l ) s . (u+s) ) / 2 pe intervalul de timp 0 ; t2 de lungime u + s .
c) Cheltuieli medii de penurie cp.lt.(r + t) / 2 pe intervalul de timp t2 ; t4 de lungime r + t .
Cheltuielile totale pe unitatea de timp sunt :
f(s,u,t,r) = ca + cs . (m l ) s . (u+s) ) / 2 + cp.lt.(r + t) / 2 / ( r + t + u + s)
Din relatiile (1) si (2) rezulta : s = l u / (m l) si r = l t / (m l) asa ca avem :
(3) f(u,t) = ca (m l ml( cs.u2 + cp.t2 ) / 2 m(u + t)
Anuland derivatele partiale f / u = 0 ; f / t = 0 gasim solutia care se dovedeste a fi punct de minim :
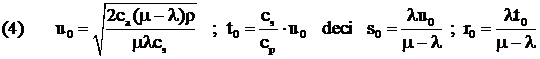
Cheltuelile totale minime pe unitatea de timp sunt f0 = f ( u0, t0) .
In cazul cind cs este neglijabil in raport cu cp deci r 0 , penuria dispare deci avem t = r = 0 asa ca f(u) = ca(m l ml.cpt2 / 2 ml) iar f '(u) = 0 are solutia :
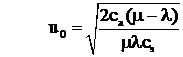
care este punct de minim . Valoarea minimului este f0 = f(u0)
Exemplu
La o ferma zootehnica avem costul de lansare a bazei furajere ca = 1200 lei , cel de stocare este
cs = 0.5 lei / tona.zi iar cel de penurie este cp = 3.5 lei / tona.zi . Avem m = 0.5 tone / zi si l = 0.4 tone / zi.
Se cer valorile optime u0 , t0 , s0 , r0 si f0 .
Solutie
Avem r = cp / (cs + cp ) = 0.875 deci din relatiile (4) rezulta :
u0 = 45.8 zile ; t0 = 6.55 zile ; s0 = 183.2 zile ; r0 = 26.2 zile .
Valoarea f0 = f ( u0 , t0 ) rezulta din relatia (3) .
Avem t1 = s0 = 183.2 zile ; t2 = s0 + u0 = 229 zile ; t3 = s0 + u0 + t0 = 235.55 zile si
t4 = s0 + u0 + t0 + r0 = 261.75 zile .
In intervalul 0 ; 183.2 zile se ofera m s0 = 96 tone furaje si se consuma l s0 = 73.28 tone furaje deci in a 183.2 - zi avem stocul de 22.72 tone furaje .
In intervalul 183.2 zile ; 229 zile se consuma in intregime stocul de 22.72 tone furaje .
In intervalul 229 zile ; 235.55 zile se creeaza un deficit de stoc de l t0 = 26.2 tone de furaje .
In intervalul 235.55 zile ; 261.75 zile se reia oferta de m r0 = 13.1 tone furaje si se consuma
l r0 = 10.48 tone furaje iar deficitul de furaje dispare in a 261.75 - zi .
In continuare procesul de oferta si consum se reia cu aceiasi paramatri optimi .
C. Stocuri optime cu cerere aleatoare
In modelul stocurilor optime cu cerere constanta de la punctul 2) s-a presupus ca cererea de r articole pentru a fi depuse in stoc este constanta si egala fie cu numarul n de articole planificate pentru stocuri cu articloe sufuciente fie cu numarul m ≤ n de articole realizate pentru stocuri cu penurie de articole .
Vom presupune mai departe ca cererea r este o variabila aleatoare pe fiecare perioada de timp de lungime t cu densitatea de probabilitate p(r) .
Cererea fiind variabila , in orice perioada de timp de lungime t sunt posibile cazurile :
r ≤ m sau r > m .
Cazul r ≤ m , ilustrat in figura 1 , duce la scaderea liniara a stocului de la m la m - r articole deci avem stocul mediu : [m+(m-r)t] / (2t) = m - (r / 2 )
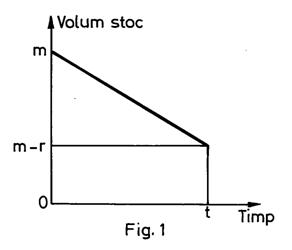
Cazul r > m , ilustrat in figura 2 , duce la scaderea liniara a stocului de la m la 0 pe subperioada de timp [0 ; u] de lungime u deci avem stocul mediu (mu) / (2t) = (m2 ) / (2r ) caci din asemanarea triunghiurilor dreptunghice OAB si ACD din figura 2 , rezulta u / t = m / r deoarece AC = r .
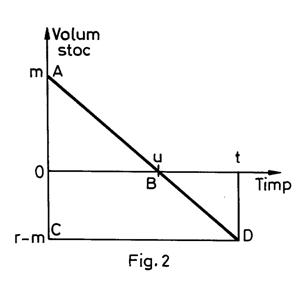
Pe subperioada de timp [u ; t ] de lungime t - u avem penurie de n - m articole deci penuria medie este [(r-m).(t-u)] / (2t) = (r-m)2 / (2r) deoarece din relatia de asemanare u / t = m / r rezulta
(t-u) / t = (r-m) / r .
Costul mediu de aprovizionare-stocare-penurie pe perioada de timp de lungime t este :
![]()
Valoarea optima m0 a lui m este data de dubla inegalitate
:
C (m - 1) > C (m) < C (m+1)
Dar :
![]()
deci cu notatia :
![]()
relatia C (m) < C (m+1) devine : cp < (cs+cp).L(m) si cum r = cp / ( cs + cp ) rezulta :
r < L(m) .
In mod analog avem :
![]()
deci relatia C (m -1) > C (m) devine : cp > (cs + cp ).L(m-1) adica r > L(m-1) .
Am demonstrat :
Teorema 3
m 0 este acea valoare a lui m care satisface dubla inegalitate : L(m-1) < r < L(m) .
Exemplu
Un depozit trebuie sa stocheze ingrasaminte chimice pentru un anumit timp.
Cererea de ingrataminte chimice (tone / luna ) este variabila aleatoare X cu repartitia :
![]()
Avem ca = 200 lei / luna ; cs = 4 lei / tona.luna ; cp = 36 lei / tona.luna.
Se cere volumul optim m0 al unei serii de aprovizionare realizate si cheltuielile medii minime C (m0) de aprovizionare , stocare si penurie .
Solutie
Avem n = 4 ; r
Avem tabelul de calcul :
|
m |
r |
p(r) |
p(r) / r |
S |
P(r ≤ m) |
L(m) |
Aici am folosit notatia :
![]()
Avem L(1) =0.845 < ρ = 0.9 < L(2)= 0.950 deci m0 = 2 tone / serie realizate .
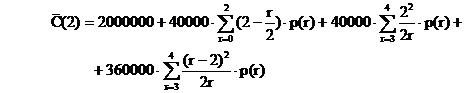
adica C (2) = 212.2 lei = minim .
Functii Douglas-Cobb
Fie x1 = cheltuieli materiale anuale ; x2 = cheltuieli cu forta de munca ; y = venitul
anual , toate la cultura porumbului in lei .
Avem y = A0 x1B1x2B2 cu 0≤ B1 , B2 ≤ 1 si B1+B2 ≠ 1 .
Profitul annual este : P(x1,x2) = A0 x1B1x2B2 - x1 - x2 si trebuie sa fie maxim .
Anulam derivatele partiale ale lui P in raport cu x1 , x2 :
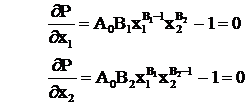
Rezulta :
![]()
adica x1 / B1 = x2 / B2 de unde x2 = (B2 / B1 ) . x1 si prima ecuatie a sistemului da :
![]()
si x20 = ( B2 / B1 ).x10 adica :
![]()
Profitul maxim este Pmax = A0 x10B1x20B2
- x10 - x20 .
Ca si in exemplul 1) se verifica faptul ca avem un punct de maxim .
5) Optimizarea nivelului preturilor de vinzare ale produselor agricole
Se urmareste maximizarea venitului din vinzarea produselor agricole, a stimularii consumului de produse agricole ca o cale principala de relansare a productiei agricole .
Vom relua optimizarea separata a cate unui produs agricol care a fost prezentata in capitolul 7
apoi vom optimiza ansamblul a doua produse agricole concurentiale.
Cazul unui produs agricol
Fie x pretul de vinzare variabil (lei / Kg) al unui produs agricol , fie y cantitatea variabila din produs , vanduta intr-un interval de timp de lungime T , la pretul de vanzare x si fie z =x.y valoarea variabila in lei a cantitatii vandute la pretul de vanzare x .
Fie xc pretul de vanzare curent al produsului , fie yc cantitatea vanduta la pretul de vinzare curent xc si fie zc = xc.yc valoarea in lei a cantitatii vandute la pretul de vanzare curent xc .
Fie xp un pret de vanzare de proba pentru testarea pietii , pentru care avem in acelasi interval de timp de lungime T , cantitatea de produs vanduta yp si valoarea in lei a cantitatii vandute zp la pretul de vanzare xp.
Este clar ca avem functia y = f(x) descrescatoare in raport cu x , datorita limitarii puterii de
cumparare a cumparatorilor potentiali .Avem z = x.f(x) .
Dorim sa calculam pretul de vanzare economic xe pentru care valoarea in lei a cantitatii vandute ze = xe.f(xe) este maxima .
Daca cantitatea de produs y scade direct proportional odata cu cresterea pretului de vinzare x , cantitatea de produs vanduta are forma y = a.x + 2b cu a < 0 .
Coeficientii a , b se gasesc din conditiile :
yc = a.xc + 2b ; yp = a.xp + 2b
deci a = (yp - xc) / (xp - xc) ; b = (xpyc - xcyp) / 2.(xp - xc )].
Avem z = x.y = a.x2 + 2.b.x deci z = maxim pentru z' = 2a.x + 2.b = 0
asa ca xe = b / ( - a) deci ye = b si ze = xe.ye = maxim .
Exemplu
Un vanzator a vandut intr-o piata cu pretul curent xc = 2.5 lei / Kg in T = 3 zile , o cantitate yc = 30 kg mere ionatan pentru care a primit suma zc = 75 lei .
In continuare a vandut la aceeasi piata cu pretul de proba xp = 3 lei / Kg tot in T = 3 zile , o cantitate
yp = 25 Kg mere ionatan pentru care a primit suma zp= 75 lei.Din formulele de mai sus rezulta
a = -10 ; b = 27.5 deci pretul de vinzare economic xe = 2.75 lei /Kg cu care in T = 3 zile , s-ar vinde cantitatea ye = 27.5 Kg mere ionatan si s-ar primi suma maxima ze = 75.625 lei .
Un alt vanzator a vandut in alta piata cu pretul curent xc = 3 lei / Kg in T = 3 zile , o cantitate yc = 20 kg mere golden pentru care a primit suma zc = 60 lei .
In continuare a vandut la aceeasi piata cu pretul de proba xp = 3.5 lei / Kg tot in T = 3 zile , o cantitate
yp = 17 Kg mere golden pentru care a primit suma zp= 59.5 lei.Din formulele de mai sus rezulta
a = - 6 ; b = 19 deci pretul de vinzare economic xe = 3.17 lei /Kg cu care in T = 3 zile , s-ar vinde cantitatea ye = 19 Kg mere golden si s-ar primi suma maxima ze = 60.17 lei .
Cazul a doua produse agricole
Daca cei doi vanzatori ar vinde produsele lor in aceeasi piata , merele ionatan si golden fiind produse concurentiale , valoarea totala a vanzarilor celor doua soiuri de mere este mai mica decat valoarea vanzarilor pentru fiecare soi in parte adica z1 = (-10x12 + 55 x1 ) si respectiv z2 = (- 6x22 + 39 x2 ) , avind forma :
z = (-10x12 + 55 x1 ) + (- 6x22 + 39 x2 ) + (2 a12 x1x2 ) cu a12 < 0 .
Daca cele doua produse ar fi fost complementare (de exemplu mere si pere) am fi avut a12 > 0 .
Valoarea coeficientului de concurenta a12 se determina astfel :
Cei doi vinzatori vand soiurile lor de mere in aceeasi piata cu preturile x1c = 2.5 lei / Kg mere ionatan si respectiv x2c = 3 lei / Kg mere golden timp de T = 3 zile si volumul vanzarilor impreuna este zc = 115.05 lei .Inlocuim pe x1 cu 2.5 , x2 cu 3 si z cu 115.05 in relatia (1) si gasim a12 = -1.33 deci valoarea vanzarilor ambelor soiuri de mere in aceeasi piata are forma:
z = (-10x12 + 55 x1 ) + (- 6x22 + 39 x2 ) + (- 2.66 x1x2 )
Anulam derivatele partiale ale lui z in raport cu x1 si x2 :
z / x1 = -20x1 + 55 - 2 .66x2 = 0 ; z / x2 = -12x2 + 38 - 2.66x1 = 0
Solutia acestui sistem liniar este x1e = 2.4 lei / Kg mere ionatan ; x2e = 2.64 lei / Kg mere golden .
Aceasta solutie este punct de maxim pentru functia z deoarece :
z / x12 = - 20 < 0 ; z / x22 = -12 < 0 si z / x1 x2 = -2.66 deci :
d z / x12). ( z / x22) - z / x1 x2)]2 = (-20).(-12)- (-2.66)2 > 0 .
Valoarea maxima a volumului vanzarilor pentru cele doua soiuri de mere impreuna , se obtine
din relatia (2) , inlocuind pe x1 cu 2.4 si pe x2 cu 2.64 si gasim ze = 1169 lei = Maxim.
Valoarea volumului vanzarilor pentru merele ionatan este z1 = (-10x12 + 55 x1 ) + (- 1.33 x1x2 )
iar valoarea volumului vanzarilor pentru merele golden este z2 = (- 6x22 + 39 x2 ) + (- 1.33 x1x2 )
Pentru x1 = 2.4 si x2 = 2.64 avem z1e = 65.97 lei si z2e = 52.72 lei iar ze = z1e+z2e =1169 lei.
Volumul vanzarilor pentru merele ionatan este y1 = (-10x1 + 55 ) + (- 1.33 x2 ) iar volumul vanzarilor pentru merele golden este y2 = (- 6x2 + 39 ) + (- 1.33 x1 ) . Pentru x1 = 2.4 si x2 = 2.64
obtinem valorile optime ale volumelor vanzarilor : y1e = 27.49 Kg mere ionatan ; y2e = 19.97
Kg mere golden .
3 Extreme cu legaturi ale functiilor de n variabile reale
Fie functia reala de n variabile reale y = f (x1,.,xn) , f: A Rn B R si fie
functiile auxiliare y = φi (x1,.,xn) ; φi : A Rn R ; (i=1,.,m). Se presupune ca functiile f ; φ1,., φm (m ≤ n) au derivate partiale continue pe A .
In plus functiile auxiliare φi se presupun functional independente pe A adica matricea
lor Jacobi J = [ ∂ φi / ∂ xj ] (x) cu m liniii si n coloane , are rangul m pentru orice vector x I A .
Fie D A multimea vectorilor x = (x1,.,xn) care anuleaza cele m functii auxiliare :
φ1 (x1,.,xn) = 0
jm (x1,.,xn) = 0
Vectorul x(0) = (x10,.,xn0) I A Rn se numeste punct de extrem conditionat pentru
functia f cu legaturile date de relatia (1) , daca el maximizeaza / minimizeaza functia f
si in plus verifica legaturile (1) adica x(0) ID .
Daca de exemplu in matricea Jacobi J de rang m , este nenul minorul :
D = Det ji xj i , j m ) , atunci din legaturile (1) putem afla pe x1,.,xm
in functie de xm+1,., xn :
x1 = y (xm+1,., xn )
xm = ym (xm+1,., xn )
In acest caz functia initiala y = f (x1,.,xn) devine :
f (x1,.,xn) = f y (xm+1,., xn ) ,., ym (xm+1,., xn ) ; xm+1,., xn = g (xm+1,., xn ) .
x(0) este punct de extrem conditionat pentru functia f cu legaturile (1) daca si numai daca x (0) = ( y (xm+1,0,., xn,0 ) ,., ym (xm+1,0,., xn,0 ) ; xm+1,0 ,., xn,0 ) este punct de
extrem neconditionat pentru functia g (xm+1,., xn ) .
Din pacate , obtinerea explicita a relatiilor (2) din relatiile (1) este in general foarte laborioasa deci vom inlocui functia g (xm+1,., xn ) cu functia Lagrange :
L (x1,., xn ) = f (x1,., xn ) - l j (x1,., xn ) - . - lm jm (x1,., xn )
Sunt valabile urmatoarele afirmatii :
Orice punct de extrem conditionat x(0) al functiei f cu legaturile (1) este punct
stationar al functiei Lagrange adica :
![]()
Se procedeaza prin reducere la absurd : daca relatiile (3) nu sunt indeplinite pentru
X(0) = (x10,.,xn0 ) , atunci x(0) nu este punct de extrem conditionat pentru functia f cu legaturile (1) .
Punctele stationare ale functiei Lagrange se afla din sistemul de ecuatii (3) + (1)
adica n + m ecuatii cu n + m necunoscute : x1,.,xn ; l lm
Valorile l lm se numesc multiplicatori Lagrange si din relatiile (3) rezulta :
![]()
Valoarea multiplicatorului Lagrange li este egala cu variatia functiei-obiectiv df
provocata de variatia functiei din legatura numarul i cu o unitate : d j i = 1 .
Din acest motiv multiplicatorii Lagrange l lm se munesc preturi-umbra sau
costuri de oportunitate prin analogie cu variabilele duale proprii yi din programarea
liniara ( Vezi cap. 6 )
Un vector x(0) I Rn - m este punct stationar al functiei g (xm+1,., xn ) daca si numai daca
x(0) I Rn este punct stationar al functiei Lagrange .
Afirmatiile (1) si (2) dau conditia necesara ca x(0) sa fie punct de extrem conditionat pentru functia f cu legaturile (1) si anume x trebuie sa fie punct stationar
al functiei Lagrange .
Urmeaza sa stabilim o conditie suficienta ca x trebuie sa fie punct stationar al
functiei Lagrange .
Din legaturile (1) obtinem prin diferentiere :
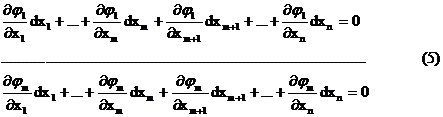
Relatiile (5) constituie un sistem de m ecuatii independente cu n necunoscute :
dx1 ,.,dxm ,dxm+1 ,.,dxn ,coeficientii fiind elemente ale matricii Jacobi de rang maxim egal cu m .
Daca avem minorul nenul : D = Det ji xj i , j m ) , din sistemul (5) putem afla pe dx1 ,.,dxm in raport cu dxm+1 ,.,dxn :
dx1 = c1 (dxm+1 ,.,dxn )
........... (6)
dxm = cm (dxm+1 ,.,dxn )
Solutiile din relatiile (6) verifica si relatia :
![]()
Conditiile suficiente de extrem conditionat pentru functia f cu legaturile (1) sunt echivalente cu conditiile de extrem neconditionat pentru functia g si acestea sunt :
a) x(0) I Rn - m trebuie sa fie punct stationar pentru functia g adica :
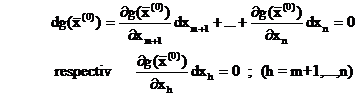
b) Diferentiala de ordinul doi a lui g in x(0) :
![]()
trebuie sa fie pozitiv definita pentru ca x(0) sa fie punct de minim si respectiv negativ definita pentru ca x(0) sa fie punct de maxim .
Mai departe , conditiile a) , b) pentru functia g se transfera functiei Lagrange L
astfel :
Conform afirmatiei 2) conditia a) devine pentru functia Lagrange L :
c) x(0) I Rn trebuie sa fie punct stationar al functiei Lagrange adica :
![]()
adica relatiile (3) :
![]()
la care se asociaza legaturile (1) deci avem n+m relatii satisfacute de n+m solutii :
x(0) = (x10,.,xn0 ) si L(0) = (l10,., lm0 ) .
Pentru a transfera conditia b) pentru functia g in conditia d) pentru functia Lagrange
L , trebuie sa diferentiem legaturile (1) pentru a obtine relatiile (5) , pe care le rezolvam in raport cu dx1,.,dxm obtinand relatiile (6) si in final inlocuim pe dx1,.,dxm date de relatiile (6) in diferentiala de ordinul al doilea a lui L .
Avem :
![]()
care dup inlocuirea lui dx1,.,dxm devine :
![]()
Conditia b) devine :
d) Diferentiala d2 L(x(0)) cu variabilele dxm+1,.,dxn , trebuie sa fie pozitiv definita
pentru ca x(0) sa fie punct de minim si respectiv sa fie negativ definita pentru ca x(0) sa
fie punct de maxim .
Exemple
Se cere extremul functiei f = - x12 - 2x22 - 3x32 +2x1+4x2+6x3 cu legatura :
j = x1+2x2+3x3 -12 = 0
Solutie
Avem functia Lagrange L = f - l j
a) Anulam derivatele partiale ale lui L in raport cu x1,x2,x3 si adaogam legatura :
L / x1 = - 2x1+2 - l = 0
L / x2 = - 4x2 +4 -2l
L / x3 = - 6x3 +6 -3l
x1+2x2+3x3 -12 = 0
Din primele trei ecuatii aflam pe x1,x2,x3 in functie de l si ii inlocuim in a patra ecuatie .
Obtinem l = -2 de unde x10 = x20 = x30 =2 adica punctul stationar al functiei Lagrange L .
Avem diferentiala de ordinul intai a lui L :
dL = (- 2x1+2 - l)dx1+( - 4x2 +4 -2l)dx2 + (- 6x3 +6 -3l)dx3 s 0 pentru valorile l
si x10 = x20 = x30 =2 .
b) Diferentiala de ordinul doi a lui L este : d2 L = - 2dx12 -4dx22 - 6dx32
Diferentiem legatura : dx1+2dx2+3dx3 = 0 de unde dx1 = -2dx2-3dx3 pe care il
inlocuim in d2L si obtinem : d2 L = - 12x22 -24x2x3 -24x32 cu Hessiana in x(0) :
![]()
Avem minorii principali : D = -12 <0 ; D = Det(H) = 144 > 0 deci avem un maxim .
Interpretarea lui l
Pentru x1 variabil si x20 = x30 = 2 avem f = - x12 + 2x1 si j = x1 -2
Avem f / x1 = - 2x1+2 ; j x1 =1 deci pentru x1=x10 = 2 obtinem :
f / x1)0 = -2 si ( j x1)0 =1 iar raportul acestor marimi este chiar l
2) Se cere extremul functiei f = - x12 - 4x22 - 9x32 +2x1+8x2+18x3 cu legaturile :
j = x1+2x2+3x3 +3 = 0 ; j = 6x1+2x2+3x3 +30.5 = 0
Solutie
Avem functia Lagrange L = f - l j l j
a) Anulam derivatele partiale ale lui L in raport cu x1,x2,x3 si adaogam legaturile :
L / x1 = - 2x1+2 - l l = 0
L / x2 = - 4x2 +8 -2l l
L / x3 = 18x3 +18 -3l l
x1+2x2+3x3 +3 = 0
x1+2x2 +3x3+30.5 = 0
Din primele trei ecuatii aflam pe x1,x2,x3 in functie de l si l si ii inlocuim in a patra si a cincea ecuatie .
Obtinem l l = 2 de unde x10 = - 5.5 ; x20 = 0.5 ; x30 =0.5 adica punctul stationar al functiei Lagrange L .
Avem diferentiala de ordinul intai a lui L :
dL = (- 2x1+2 - l l )dx1+( - 4x2 +8 -2l l )dx2 + (18x3 +18 -3l l = 0)dx3 s 0 pentru valorile l l = 2 si x10 = - 5.5 ; x20 = 0.5 ; x30 =0.5
b) Diferentiala de ordinul doi a lui L este : d2 L = - 2dx12 -4dx22 +186dx32
Diferentiem legaturile : dx1+2dx2+3dx3 = 0 si 6dx1+2dx2+3dx3 = 0 de unde aflam pe dx1 si dx2 in raport cu dx3 : dx1 = 0 ; dx2 = -1.5 dx3 pe care le inlocuim im d2L si obtinem : d2 L = 9dx32 .
Cum D = 9 > 0 avem un minim .
Interpretarea lui l
Pentru x1 variabil si x20 = - 5.5 ; x30 = 0.5 avem f = - x12 + 2x1 + 9.75 si
j = x1 +5.5 ; j = 6x1 +33
Avem f / x1 = - 2x1+2 ; j x1 =1 ; j x1 =6 deci pentru x1=x10 = 5.5 obtinem :
f / x1)0 = 13 si ( j x1)0 =1 ; ( j x1)0 =6 deci se verifica relatia :
f / x1)0 = l j x1)0 + l j x1)0 adica 13 = 1 x 1 + 2 x 6 .
Aplicatii
I) Cilindrul optim
i) Problema primala :
Dintr-o foaie de tabla de suprafata data S=S0 sa se confectioneze o cutie cilindrica
pentru conserve , de volum maxim .
Solutie
Fie x1 raza bazei si x2 generatoarea cilindrului. Suprafata totala a cilindrului este
S=2px1(x1+x2) iar volumul cilindruui este V = px12x2 .
Avem problema de extrem cu legaturi primala :
V = px12x2 = maxim ;
S=2px1(x1+x2) = S0
Functia Lagrange este L = px12x2 - l px1(x1+x2) - S0
Anulam derivatele partiale ale lui L in raport cu x1 si x2 , si atasam legatura :
L / x1 = 2px1x2 pl x1 + x2) = 0
L / x2 = px12 - 2plx1 = 0
px1(x1+x2) - S0 = 0
Rezolvand acest sistem avem l = (S0 / 24p)1/2 si punctul stationar cu componente pozitive : x10 = (S0 / 6p)1/2 ; x20 = 2x10 .
Ca si in exemplul 1 ) de mai sus se arata ca acest punct stationar este punct de maxim.
Avem Vmax = (S03 / 54p)1/2 de unde se verifica relatia l = dV / dS0 .
ii) Problema duala :
Dintr-o foaie de tabla ve volum dat V0 sa se confectioneze o cutie cilindrica pentru
conserve , de arie totala minima .
Solutie
Avem problema de extrem cu legaturi duala :
S=2px1(x1+x2) =minim
V = px12x2 = V0
Formam functia Lagrange L = px1(x1+x2) - m px12x2 - V0)
Anulam derivatele partiale ale lui L in raport cu x1 si x2 , si atasam legatura :
L / x1 = 2p(2x1+x2 p m.x1 x2 = 0
L / x2 = 2px1 - p mx12 = 0
px12x2 - V0 = 0
Rezolvand acest sistem avem m p / V0)1/3 si punctul stationar cu componente pozitive : x10 = (V0 / 2p)1/3 ; x20 = 2x10 .
Ca si in exemplul 1 ) de mai sus se arata ca acest punct stationar este punct de minim.
Avem Smin = ( 54pV02)1/3 de unde se verifica relatia m = dS / dV0 .
In ambele probleme de optimizare avem x20 =2x10 deci cutia cilindrica optima are diametrul bazei cilindrului egal cu generatoarea cilindrului .
II) Grinda dreptungiulara optima
Dintr-un bustean cilindric cu sectiunea circulara de diametru D trebuie cioplita o grinda cu scetiunea dreptunghiulara.
Sa se afle dimensiunile x1 , x2 ale sectiunii dreptunghiulare satfel ca rezistenta sa sa fie maxima .
Solutie
Rezistenta grinzii este R = kx1x22 unde x1 este lungimea pe orizontala a setiunii dreptunghiulare iar x2 este inaltimea pe verticala a sectiunii dreptunghiulare .
Avem legatura : x12 + x22 D2 .
Problema de extrem cu legaturi are forma :
R = kx1x22 = maxim
x12 + x22 - D2 = 0
Functia Lagrange este : L = kx1x22 - l.( x12 + x22 - D2 )
Anulam derivatele partiale de ordinul intai ale lui L in raport cu x1 , x2 si atasam
legatura :
L / x1 = kx22 - 2lx1 = 0
L / x2 = 2kx1x2 - 2lx2 = 0
x12 + x22 - D2 = 0
Din primele doua ecuatii avem : x1 = l / k ; x2 = 21/2l / k care se inlocuiesc in a treia
ecuatie si rezulta : l = (3)1/2kD / 3 deci avem punctul stationar :x10 = (3)1/2D / 3 ;
x20 = (6)1/2D / 3 .
Ca si in exemplul 1) de mai sus se verifica daptul ca avem un punct de maxim .
Valoarea rezistentei maxime este Rmax = 2(3)1/2kD3 / 9 .
Se vede ca intre dimensiunile sectiunii dreptunghulare optime exista relatia :
x20 = (2)1/2x10 .
III) Functia Douglas-Cobb cu legaturi
Fie x1 cheltuielile materiale anuale la cultura porumbului (lei) ; x2 cheltuielile cu forta de munca anuale la cultura porumbului (lei ) si y venitul anual la cultura porumbului (lei ). Avem functia Douglas-Cobb y = A0x1B1x2B2 unde 0 B1 , B2 1 si B1+B2
B1 si B2 sunt elasticitatile venitului y in raport cu cheltuielile x1 , x2 .
Problema de optimizare primala :
Sa se maximizeze venitul cu incadrarea cheltuielilor de productie in suma C0 .
Avem problema de extrem cu legaturi :
y = A0x1B1x2B2 = maxim ;
x1+x2 - C0 = 0
Avem functia Lagrange : L = A0x1B1x2B2 - l( x1+x2 - C0 )
Anulam derivatele partiale de ordinul intai ale lui L in raport cu x1 si x2 si atasam
legatura :
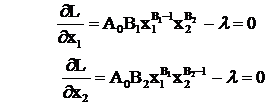
Din primele doua ecuatii rezulta x1 / B1 = x2 / B2 si impreuna cu ecuatia a treia dau :
x 10 = (B1C0 ) / (B1 +B2) ; x 20 = (B2C0 ) / (B1 +B2) asa ca :
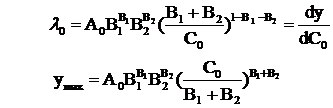
Ca si in exemplul 1) de mai sus se arata ca in adevar avem un punct de maxim .
Problema de optimizare duala
Sa se minimizeze cheltuielile cu garantarea venitului in valoare de cel putin V0 .
Avem problema de extrem cu legaturi :
y = x1+x2 =minim
A0x1B1x2B2 = V0
Avem functia Lagrange : L = x1 + x2 - m(A0x1B1x2B2 - V0 )
Anulam derivatele partiale de ordinul intai ale lui L in raport cu x1 si x2 si atasam
legatura :
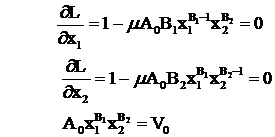
Din primele doua ecuatii rezulta x1 / B1 = x2 / B2 si impreuna cu ecuatia a treia dau :
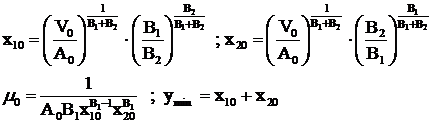
Ca si in exemplul 1) de mai sus se arata ca in adevar avem un punct de minim .
4 Metoda Newton-Raphson pentru sisteme neliniare
Punctele de minim / maxim ale functiilor reale de n variabile reale se afla printre punctele lor stationare adica sunt solutii ale unor sisteme neliniare obtinute prin anularea derivatelor partiale de ordinul intai ale functiei .
Pentru rezolvarea unor asemenea sisteme neliniare exista metode de rezolvare iterative .
Una din cele uzuale se numeste metoda Newton-Raphson si o vom prezenta in continuare .
Fie sistemul neliniar de n ecuatii cu n necunoscute x1,.,xn :
f1(x1,.,xn) = 0
......
fn(x1,.,xn) = 0
unde functiile f1,.,fn au derivate partiale continue pe R n in raport cu x1,.,xn .
Cu notatiile X = (x1,.,xn )T , F = (f1,.,fn )T , sistemul neliniar se scrie vectorial :
F(X) = 0 .
Fie α = (α1 , . ,αn)T solutia exacta a sistemului neliniar .
Fie Jacobianul functiilor f1,.,fn in raport cu variabilele x1,.,xn :
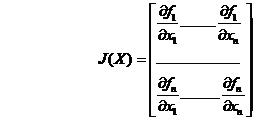
Presupunem ca Det(J(X)) ≠ 0
in sfera S(α , ε ) = deci in aceasta sfera
exista matricea inversa J(X)
Fie sirul de vectori definit recurent :
(5) X(p) X(p -1 ) J( X(p - 1 ) - 1.F(X(p - 1 )
cu X(0) = ( x1,0,.,xn,0)T I S(α , ε ) ; X(p = ( x1,p.,xn,p )T I R n .
Pentru convergenta sirului de vectori X(p) catre radacina
α = (α1 , . ,αn)T a sistemului neliniar , sunt suficiente conditiile :
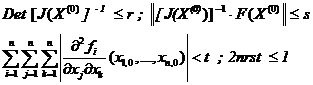
Fie m numarul de iteratii ale sirului recurent : X(0),
X(1) , ., X(m - 1 ) , X(m) .
![]()
Eroarea postcalculata
dupa m iteratii este :
Eroarea de verificare dupa m iteratii este :
![]()
Se poate alege acel numar de iteratii m pentru care sunt asigurate valori prestabilite pentru e e
Caz particular
Fie sistemul polinomial patratic :
f1(X) = XT.A1.X +b1.X +c1 =0
fn(X) = XT.An.X +bn.X +c1 =0
Pentru alcatuirea Jacobianului J(X) = ∂ f i / ∂ x j ; (i,j = 1,2,.,n) folosim relatiile :
![]()
Presupunem Det[J(X)]≠0 intr-o vecinatate a
solutiei exacte α =
(α1 , . ,αn)T I R n .
Matricile numerice J(X(0)) , J(X(1)) , ., J(X(m)) care apar in relatiile de recurenta (5) se vor inversa cu programul INVMAT .
Exemplu
Sa se rezolve sistemul patratic :
x12 +x22 +x32 - 1 = 0
2x12 + x22 - 4 x3 = 0
3x12 +x32 - 4 x2 = 0
prin metoda iterativa Newton-Raphson .
Solutie
Luam :
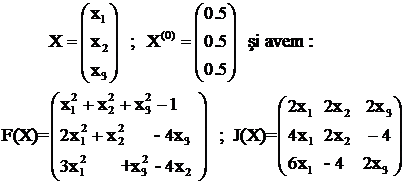
Calculam :
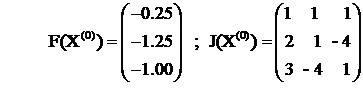
de unde rezulta :
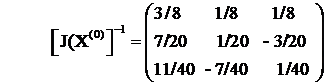
Din relatiile de recurenta (1) rezulta :
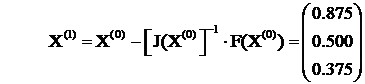
Mai departe calculam F(X(1)) , J(X(1)) si J(X(1) - 1 de unde rezulta :
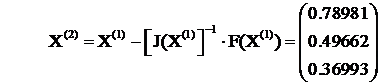
In mod analog din X(2) obtinem pe X(3) :
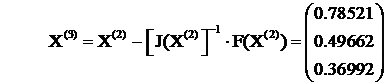
In fine dupa m = 4 iteratii avem :
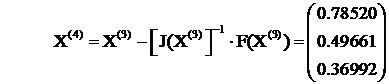
ceace asigura precizia EPS = 0.0001 .
Eroarea postcalculata este : Ep = 0.0000135 iar cea de verificare este EV = 0.0000638
Programul SISPAT face aceste calcule .
In capitolul 10 vom folosi acest program pentru optimizari neliniare .
Rezumat
In acest capitol se defineste functia reala de n variabile reale , se prezinta rolul derivatelor partiale de ordinul unu si doi in studiul functiei , in special la gasirea maximelor si minimelor libere sau cu legaturi ale functiei . Capitolul se incheie cu o metoda iterativa de rezolvare a unui sistem neliniar de ecuatii cu computerul .
Intrebari
Care este rolul derivatelor partiale de ordinul unu in studiul functiei de n variabile reale ?
Care este rolul derivatelor partiale de ordinul doi in studiul functiei de n variabile reale ?
Cum se gasesc maximele si minimele libere sau cu legaturi ale unei functii de n variabile reale ?
Ce aplicatii au stocurile in agricultura ?
7 Bibliografie
Stanasila O. " Analiza liniara si geometrie "Vol. I - II,Editura ALL ,2000 - 2001
Cenusa Gh. si col." Matematici pentru economisti " Editura CISON,2000
Cenusa Gh. si col." Matematici pentru economisti - culegerede probleme" Editura CISON,2000
4. Ene D. " Matematici (I) " Editura CERES , 2004
5. Gogonea S. , Ene D. " Analiza numerica " Editura Cartea Universitara , 2005
6. Ene D.,Gogonea S. "Metode numerice" Editura Cartea Universitara , 2005
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1671
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved