| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Cuadrice date prin ecuatii reduse
Fie in spatiul punctual euclidian E reperul ortonormat R (O;![]()
Reamintim ca distanta dintre doua puncte in spatiu , M(x1,y1,z1) si respectiv N(x2,y2,z2), este data de
d(M,N) = ![]()
Sfera. Fie C I E3 un punct dat .
|
1 Definitie. |
Se numeste sfera de centru C si raza rIR multimea punctelor M I E cu proprietatea d( M,C ) = r . |
Multimea punctelor M(x,y,z) I E3 care apartin sferei (S) de centru C(a,b,c) si raza r satisfac relatia :
(x - a)2 + (y - b)2 + (z - c)2 = r2 (1)
numita ecuatia carteziana implicita a sferei (sub forma de patrate restranse).
Dezvoltand ecuatia (1) obtinem
x2+ y2 + z2 -2ax -2by - 2cz + a2 + b2 +c2 - r2 = 0,
care ne sugereaza studiul ecuatiei
A(x2 + y2 +z2 ) + Bx + Cy + Dz + E = 0, (2)
ce reprezinta ecuatia unei sfere, numita ecuatia carteziana generala a unei sfere. Ecuatia (2) poate fi pusa sub forma
x2 + y2 +z2 + 2m x + 2ny + 2pz + q = 0 , (3)
numita ecuatia carteziana generala a sferei sub forma normala, in care
coordonatele centrului C sunt date de : a = -m, b = -n, c = -p si raza
r = ![]() .
.
Sa consideram in sistemul
de coordonate carteziene Oxyz punctul
M(x,y,z) , vectorul de pozitie
corespunzator ![]() ,
, ![]() , proiectia Mo(x,y,0) a punctului M pe planul xOy, uI p) -unghiul dintre OMo si directia pozitiva a
axei Ox, respectiv vI p] - unghiul
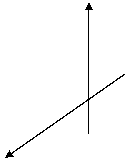
dintre OM si directia pozitiva a axei Oz (fig.1) . Obtinem
, proiectia Mo(x,y,0) a punctului M pe planul xOy, uI p) -unghiul dintre OMo si directia pozitiva a
axei Ox, respectiv vI p] - unghiul
dintre OM si directia pozitiva a axei Oz (fig.1) . Obtinem
OMo = r cos(90o- v ) = r sin v , de unde rezulta
Pentru r = const., uI p), vI p punctul M(x,y,z) se gaseste pe
sfera de raza r ,cu centrul in
origine. Din acest motiv
cantitatile r,u,v vor fi numite coordonatele sferice ale unui punct
din spatiu.
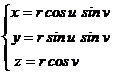
z
 M(x,y,z)
M(x,y,z)
![]()
![]()
![]()
![]()
![]() y
y
O
![]() Mo(x,y,0)
Mo(x,y,0)
Fig.1![]()
x
![]() Ecuatiile parametrice ale sferei cu centrul in punctul
C(a,b,c) si raza r pot
fi scrise sub forma
Ecuatiile parametrice ale sferei cu centrul in punctul
C(a,b,c) si raza r pot
fi scrise sub forma
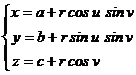 (4)
(4)
Fie o dreapta oarecare prin punctul M0(xo,yo,zo) : x = xo+ l t ,
y = yo+m t , z = zo + n t si sfera data de ecuatia (1) . Intersectia dintre sfera si dreapta se reduce la studiul sistemului format din ecuatiile acestora.
Obtinem ecuatia de gradul al doilea in t
(l2+m2+n2) t2 + 2[l(xo-a)+m(yo-b)+n(zo-c)] t + (xo-a)2+(yo-b)2+(zo-c)2-r2=0,
care ne permite sa concluzionam ca o dreapta intersecteaza o sfera in cel mult doua puncte. Daca notam t1, t2 radacinile reale ale ecuatiei de mai sus, valori corespunzatoare punctelor de intersectie M1, M2, ale sferei cu dreapa ,printr-un calcul direct obtinem ca produsul distantelor punctului Mo la punctele de intersectie M1 respectiv M2 este constant , adica
MoM1 MoM2 = t t (l2 + m2 + n2) = (xo-a)2+(yo-b)2+(zo-c)2- r2
Numarul real
![]() = (xo-a)2+(yo-b)2+(zo-c)2-
r2 = d2 - r2 (5)
= (xo-a)2+(yo-b)2+(zo-c)2-
r2 = d2 - r2 (5)
d desemnand distanta punctului Mo la centrul sferei, este numit puterea punctului Mo fata de sfera .
Fie sferele
(S1) x2 + y2 +z2 + 2m1 x + 2n1 y + 2p1 z + q 1 = 0
(S2) x2 + y2 +z2 + 2m2 x + 2n2 y + 2p2 z + q 2 = 0
Locul geometric al punctelor din spatiu cu aceeasi putere fata de sferele (S1) si (S2) este un plan perpendicular pe linia centrelor celor doua sfere,numit planul radical. Ecuatia planului radical a doua sfere se obtine scazand ecuatiile acestora,adica
2(m1-m2)x + 2(n1-n2)y + 2(p1-p2)z +q1-q2 = 0 (2,6)
Daca consideram trei sfere (S1), (S2), (S3) ,cu centrele necoliniare, atunci dreapta S1 - S2 = 0, S1 - S3=0 se numeste axa radicala a celor trei sfere.
In cazul a patru sfere, cu centrele necoplanare, exista un punct cu aceeasi putere fata de aceste sfere, numit centru radical.
Numim fascicul de sfere, multimea sferelor din spatiu care au acelasi plan radical. Planele S1 - S2 = 0 si S3 - S2 = 0 coincid daca
S3 - S2=l( S1 - S2) , lIR sau S3= l S1 +(1-l)S2 , adica multimea tuturor sferelor din fascicolul determinat de S1 si S2 este caracterizata de ecuatia
S1 + k S2 = 0 (7)
Familia sferelor din spatiu cu aceeasi axa radicala cu sferele (S1), (S2), (S3) este numita retea de sfere si este caracterizata de ecuatia
Observatie. Daca (S) este sfera de centru C si raza r , d este distanta centrului sferei la planul p ,atunci avem urmatoarele cazuri :
d < r - planul p este secant sferei (S)
d = r - planul p este tangent sferei (S)
d > r - planul p este exterior sferei (S) .
Elipsoidul.
|
2 Definitie. |
Se numeste elipsoid suprafata (E) caracterizata de ecuatia (E) |
Forma elipsoidului o putem determina studiind intersectiile acestuia cu plane paralele cu planele de coordonate.Astfel , intersectiile cu plane paralele cu planele de coordonate sunt elipsele:
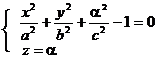 ,
, 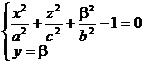 ,
, 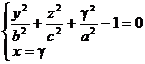 ,
,
reale pentru a < c ,b< b , respectiv g< a sau multimea vida pentru a >c ,
b> b, respectiv g> a .
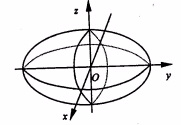
fig.2
Planele de coordonate (plane principale)sunt plane de simetrie ale elipsoidului, axele de coordonate sunt axe de simetrie,iar segmentele pe axele de coordonate de lungime egale cu a,b,respectiv c , sunt numite semiaxe. Intersectiile elupsoidului cu axele de simetrie vor fi numite varfuri.Daca doua semiaxe sunt egale ,vom obtine un elipsoid de rotatie, iar pentru a = b = c se obtine sfera.
Originea reperului este centru de simetrie pentru multimea punctelor elipsoidului,numit centrul elipsoidului.
Ecuatiile parametrice ale elipsoidului (11) sunt
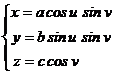 , u I p) , v I p (12)
, u I p) , v I p (12)
3 Hiperboloizi .
|
3 Definitie. |
Se numeste hiperboloid cu o panza suprafata (H1) caracterizata de ecuatia (H1) |
|
4 Teorema |
Orice punct al hiperboloidului (H1) este situat pe o dreapta din familia |
|
4 Definitie. |
Se numeste suprafata riglata , o suprafata S E generata de o dreapta care se sprijina pe o curba data. |
|
4 Definitie. |
Se numeste hiperboloid cu doua panze suprafata (H2) caracterizata de ecuatia (H2) |
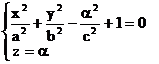
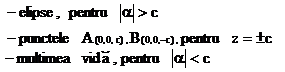
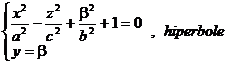
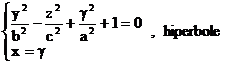
Axele si planele sistemului de coordonate sunt axe, respectiv, plane de simetrie. Punctele A(o,o,c) si B(0,0,-c) vor fi numite varfurile hiperbo-loidului cu doua panze .
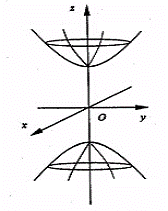
fig.4
Hiperboloidul cu doua panze (14) este caracterizat parametric de ecuatiile :
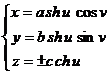 uI R , vI p (18)
uI R , vI p (18)
Paraboloizi .
|
5 Definitie. |
Se numeste paraboloid eliptic suprafata (Pe) caracterizata de ecuatia (Pe) |
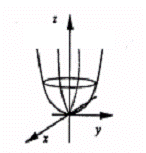
fig.5
Intersectia paraboloidului eliptic cu plane paralele cu axa Oz sunt parabole,iar intersectia cu plane paralele cu planul xOy sunt elipse pentru
z > 0,originea (varful paraboloidului) pentru z = 0,respectiv , multimea vida pentru z < 0.
Paraboloidul eliptic (17) este caracterizat parametric de ecuatiile :
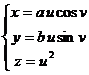 uI R , vI p (20)
uI R , vI p (20)
|
6 Definitie. |
Se numeste paraboloid hiperbolic ( sa ) suprafata (Ph), caracterizata de ecuatia (Ph) |
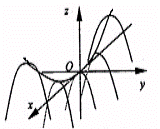
fig.5
Paraboloidul hiperbolic are aceleasi axe si plane de simetrie ca si paraboloidul eliptic.
Intersectiile paraboloidului hiperbolic cu plane paralele cu planele de coordonate sunt date de curbele :
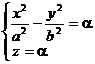
![]()
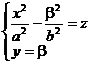
![]()
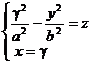
![]()
Paraboloidul hiperbolic (19) este caracterizat de ecuatiile parametrice
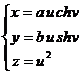 - u,v I R (22)
- u,v I R (22)
|
7 Teorema |
Paraboloidul hiperbolic este o suprafata dublu riglata |
In
adevar, ecuatia (21) poate fi scrisa sub forma ![]() , din care
obtinem familiile generatoarelor rectilinii :
, din care
obtinem familiile generatoarelor rectilinii : ![]() , date de :
, date de :
Conul, cilindrul, perechi de plane
|
7 Definitie. |
Se numeste con suprafata (C), caracterizata de ecuatia (C) |

![]()
 z
z
![]()

![]()
 y
y
![]()
![]()
Fig.7
Intersectiile conului, fig7, cu plane paralele cu planul xOy sunt elipse si intersectiile conului cu plane paralele cu axa Oz sunt hiperbole.
Ecuatiile parametrice ale conului (21) sunt date de
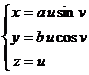 uI R , vI p
uI R , vI p
|
8 Definitie. |
Se numeste suprafata cilindrica suprafata (S caracterizata, in spatiul E , de o ecuatie in doua nedeterminate S) F x,y F(y,z) =0 sau F(x,z) =0 (25) |
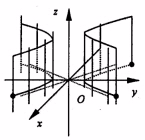
fig.7
In particular , avem :
![]() - cilindrul eliptic
, iar pentru b = a obtinem
- cilindrul eliptic
, iar pentru b = a obtinem
x2 + y2 = a2 - cilindrul circular
![]() - cilindrul
hiperbolic
- cilindrul
hiperbolic
y2 = 2px - cilindrul parabolic
Aceste suprafete cilindrice au generatoarele paralele cu axa Oz .
Alte suprafete algebrice de ordinul al doilea sunt:
![]() - plane secante
- plane secante
x2 - a2 = 0 - plane paralele (confundate, pentru a = 0)
![]() - dreapta
dubla
- dreapta
dubla
![]() - punct dublu
- punct dublu
a2x2+b2y2+c2z2+1 = 0 - multimea vida .
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2437
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved