| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Functia de gradul al doilea
Definitie. Se
numeste functie de gradul al
doilea, o aplicatie de forma ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() .
.
Exemple :
Forma canonica a functiei de gradul doi
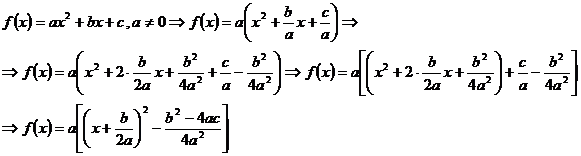 Daca notam cu
Daca notam cu ![]() , obtinem
, obtinem 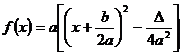 .
.
Definitie. Numarul real ![]() se numeste descriminantul functiei de
gradul al doilea .
se numeste descriminantul functiei de
gradul al doilea .
Definitie.
Ultima forma la care a fost adusa functia 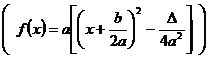 poarta numele de forma canonica a
functiei de gradul doi.
poarta numele de forma canonica a
functiei de gradul doi.
Exemple :
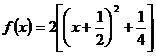 .
.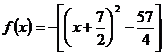 .
.
Rezolvarea ecuatiei de gradul al doilea
Definitie. Se numeste ecuatie
de gradul doi, o ecuatie de forma ![]() ,
, ![]() .
.
Dupa
cum am vazut mai sus, la forma canonica a functiei de gradul
doi, ecuatia de gradul doi ![]() ,
, ![]() se poate scrie
se poate scrie 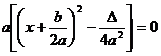 si cum
si cum ![]() , avem
, avem ![]() . Pentru rezolvarea ultimei ecuatii se disting teri
cazuri :
. Pentru rezolvarea ultimei ecuatii se disting teri
cazuri :
1)
![]() . In acest caz ecuatia nu are solutii reale
deoarece
. In acest caz ecuatia nu are solutii reale
deoarece ![]()
![]() unde membrul stang
fiind un patrat este pozitiv, iar membrul drept este raportul dintre un
numar negativ si un patrat, deci negativ.
unde membrul stang
fiind un patrat este pozitiv, iar membrul drept este raportul dintre un
numar negativ si un patrat, deci negativ.
2)
![]() . In acest caz ecuatia devine
. In acest caz ecuatia devine ![]() si solutiile
coincid
si solutiile
coincid ![]() .
.
3)
![]() . In acest caz ecuatia admite doua
radacini distincte, deoarece
. In acest caz ecuatia admite doua
radacini distincte, deoarece 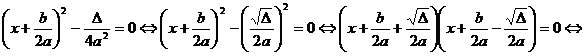
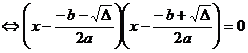 , de unde obtinem
, de unde obtinem ![]() si
si ![]() .
.
Exemple :
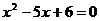 . Discriminantul este
. Discriminantul este
Observatie. Dupa
cum se poate observa foarte usor, in cazul in care avem solutii,
adica ![]() sau
sau ![]() , acestea se pot scrie
, acestea se pot scrie ![]() , deci cazurile 2) si 3) se pot restrange sub foma
:
, deci cazurile 2) si 3) se pot restrange sub foma
:
2'. ![]() .
.
Suma si produsul radacinilor ecuatiei de gradul al doilea
Observatie. Vom considera in acest paragraf
numai cazul ![]() , insa rezultatul obtinut se poate aplica si
in cazul in care
, insa rezultatul obtinut se poate aplica si
in cazul in care ![]() , caz in care nu avem radacini reale, dar avem
radacini complexe.
, caz in care nu avem radacini reale, dar avem
radacini complexe.
In cazul ![]() , radacinile sunt
, radacinile sunt ![]() si
si ![]() .
.
Suma, pe care o vom nota
cu ![]() este :
este : ![]() .
.
Produsul, pe care il
vom nota cu ![]() este :
este : 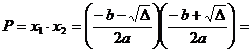
![]() .
.
Daca
rezumam, avem : ![]() si
si ![]() .
.
Observatie.
Orice ecuatie de gradul al doilea ![]() ,
, ![]() se poate scrie
se poate scrie ![]() . Intrucat
. Intrucat ![]() , ecuatia este echivalenta cu
, ecuatia este echivalenta cu ![]() , cu alte cuvinte orice ecuatie de gradul doi poate fi
scrisa sub forma
, cu alte cuvinte orice ecuatie de gradul doi poate fi
scrisa sub forma ![]() .
.
Observatie. Functia
de gradul doi ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() poate fi scrisa
sub forma
poate fi scrisa
sub forma ![]() , unde
, unde ![]() sunt
radacinile ecuatiei
sunt
radacinile ecuatiei ![]() . Rezumand putem scrie :
. Rezumand putem scrie : ![]() .
.
Exemple :
1. Sa se construiasca ecuatia
de gradul al doilea care admite ca radacini pe ![]() si
si ![]() . Suma radacinilor este
. Suma radacinilor este ![]() , iar produsul radacinilor este
, iar produsul radacinilor este 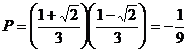 . Ecuatia se scrie
. Ecuatia se scrie ![]() , sau aducand la acelasi numitor, avem :
, sau aducand la acelasi numitor, avem : ![]() .
.
2. Fara a rezolva ecuatia 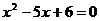 sa se determine
suma si produsul radacinilor .
sa se determine
suma si produsul radacinilor .
![]() , iar
, iar ![]() .
.
Semnul radacinilor ecuatiei de gradul al doilea
Natura si semnul radacinilor
ecuatiei de gradul doi ![]() ,
, ![]() poate fi
sintetizata in urmatorul tabel :
poate fi
sintetizata in urmatorul tabel :
|
|
P |
S |
Natura si semnul radacinilor ecuatiei |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
Radacinile nu sunt reale |
||
Semnul functiei de gradul al doilea
Consideram functia de gradul al
doilea ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() . Forma canonica a acesteia este
. Forma canonica a acesteia este 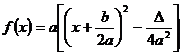 . Intervin doua posibilitati pentru semnul lui
. Intervin doua posibilitati pentru semnul lui
![]() . Le vom studia separat.
. Le vom studia separat.
1. ![]() . In acest caz, studierea semnului lui
. In acest caz, studierea semnului lui ![]() se reduce la studierea
semnului expresiei
se reduce la studierea
semnului expresiei ![]() . Se disting trei cazuri :
. Se disting trei cazuri :
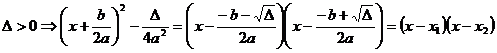 .
.Semnul functiei va fi ilustrat cu ajutorul urmatorului tabel :
|
|
|
|
|
- - - - - - - - 0 + + + + + + + + + + + |
|
|
- - - - - - - - - - - - - - - - - - 0 + + + + + |
|
|
+ + + + + 0 - - - - - - - 0 + + + + + + |
2. ![]() . Acest caz se reduce la precedentul, modificand peste tot
semnul functiei deoarece avem
. Acest caz se reduce la precedentul, modificand peste tot
semnul functiei deoarece avem 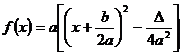 ,
, ![]() este un numar
negativ si semnul parantezei l-am studiat in primul caz.
este un numar
negativ si semnul parantezei l-am studiat in primul caz.
Observatie. Discutia de mai sus se poate rezuma astfel :
Cazul ![]()
|
|
|
|
|
semn |
Cazul ![]()
|
|
|
|
|
semn |
Cazul ![]()
|
|
|
|
|
semn |
Exemple :
1. ![]() .
. ![]() ,
, ![]() .
.
2. ![]() .
. ![]() ,
, ![]() , deci :
, deci :
|
|
|
|
|
+ + + + + + + + + 0 + + + + + + + + + + |
3. ![]() .
. ![]() , radacinile sunt
, radacinile sunt ![]() ,
, ![]() , deci :
, deci :
|
|
|
|
|
+ + + + + + + 0 - - - - - - - - - 0 + + + + + + |
Monotonia functiei de gradul doi
Reamintim urmatoarele :
Definitie. Fie ![]() o functie de
variabila reala si
o functie de
variabila reala si ![]() .
.
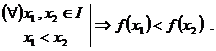
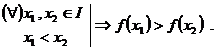
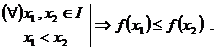
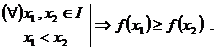
Observatie. O
functie ![]() strict
crescatoare pe
strict
crescatoare pe ![]() sau strict
descrescatoare pe
sau strict
descrescatoare pe ![]() se numeste
functie strict monotona
pe
se numeste
functie strict monotona
pe ![]() . O functie
. O functie ![]() crescatoare pe
crescatoare pe ![]() sau descrescatoare
pe
sau descrescatoare
pe ![]() se numeste monotona
pe
se numeste monotona
pe ![]() .
.
Vom studia monotonia folosind definitia precedenta :
![]() cu
cu ![]() , avem :
, avem : 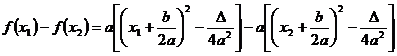
![]()
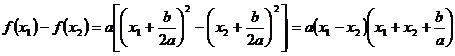 .
.
Cunoastem ca ![]() ,
, ![]() si
si ![]() ,
, ![]() sunt argumente. Pentru
a determina semnul lui
sunt argumente. Pentru
a determina semnul lui ![]() vom studia
situatiile :
vom studia
situatiile :
Consemnam monotonia functiei prin sageti in urmatorul tabel :
|
|
|
|
|
|
Consemnam monotonia functiei prin sageti in urmatorul tabel :
|
|
|
|
|
|
Observatie. In contextul casei a-XI-a, folosind notiunile de aniliza matematica, studiul monotoniei revine la studiul semnului primei derivate :
![]() .
.
Deci totul se reduce la studiul semnului
expresiei ![]() . Avem doua situatii :
. Avem doua situatii :
1. ![]()
|
|
|
|
|
- - - - - - - - 0 + + + + + +
|
|
|
|
2. ![]()
|
|
|
|
|
+ + + + + + 0 - - - - - - - -
|
|
|
|
Observatie.
Monotonia functiei de gradul al doilea este caracterizata de
coeficientul lui ![]() ,
, ![]() si
si
de argumentul ![]() .
.
Extremul functiei de gradul al doilea
De la forma canonica cunoastem egalitatea :
![]() .
.
Membrul din dreapta al egalitatii
eeste alcatuit din doi termeni. Un termen variabil ![]() pozitiv si un
termen constant
pozitiv si un
termen constant ![]() . Acest membru are cea mai mica valoare atunci cand termenul
variabil are cea mai mica valoare . Cea mai mica valoare a unei
variabile pozitive este zero, deci
. Acest membru are cea mai mica valoare atunci cand termenul
variabil are cea mai mica valoare . Cea mai mica valoare a unei
variabile pozitive este zero, deci ![]() , egalitatea realizandu-se pentru
, egalitatea realizandu-se pentru ![]() . Rezulta :
. Rezulta :
![]() . Inmultind membrii inegalitatii cu
. Inmultind membrii inegalitatii cu ![]() , obtinem :
, obtinem :
Definitie.
Punctul ![]() se numeste extremul sau varful functiei de gradul al doilea.
se numeste extremul sau varful functiei de gradul al doilea.
Observatie.
Extremul este un maxim daca ![]() si este uin minim
daca
si este uin minim
daca ![]() .
.
Exemple :
1. Sa se studieze monotonia urmatoarelor functii :
a)
![]() ,
, ![]() ;
;
b)
![]() ,
, ![]() ;
;
Solutie :
a) ![]() ,
, ![]() ,
, ![]() . Monotonia va fi ilustrata cu ajutorul urmatorului
tabel :
. Monotonia va fi ilustrata cu ajutorul urmatorului
tabel :
|
|
|
|
|
-1
|
b) ![]() ,
, ![]() ,
, ![]() . Monotonia va fi ilustrata cu ajutorul
. Monotonia va fi ilustrata cu ajutorul
urmatorului tabel :
|
|
|
|
|
25
|
2. Sa se stabileacsa maximul sau minimul urmatoarelor functii :
a)
![]() ;
;
b)
![]() ;
;
Solutie :
a) ![]() deci functia are
un maxim,
deci functia are
un maxim, ![]() ,
, ![]() , punctul de maxim este
, punctul de maxim este ![]() iar valoarea
maxima a functiei este 0.
iar valoarea
maxima a functiei este 0.
b) ![]() deci functia are
un minim,
deci functia are
un minim, ![]() ,
, ![]() , punctul de minim este
, punctul de minim este ![]() iar valoarea minima
a functiei este
iar valoarea minima
a functiei este ![]() .
.
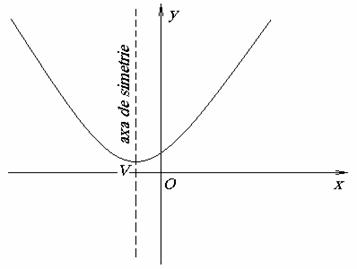
Reprezentarea grafica a functiei de gradul doi
Definitie.
Reprezentarea grafica a functiei ![]() ,
, ![]() , unde
, unde ![]() ,
, ![]() , adica multimea punctelor
, adica multimea punctelor ![]() ale caror
coordonate verifica relatia
ale caror
coordonate verifica relatia ![]() este o curba
numita parabola. Vom
nota graficul functiei de gradul al doilea cu
este o curba
numita parabola. Vom
nota graficul functiei de gradul al doilea cu ![]() .
.
Pentru reprezentarea grafica a functiei de gradul al doilea trebuiesc parcursi urmatorii pasi :
1) Intersectia graficului cu axele de coordonate.
Determinam intersectia graficului
functiei de gradul al doilea cu axa ![]() , aceasta se obtine rezolvand ecuatia
, aceasta se obtine rezolvand ecuatia ![]() . Se disting trei cazuri :
. Se disting trei cazuri :
Determinam intersectia graficului
functiei de gradul al doilea cu axa ![]() , aceasta se obtine calculand
, aceasta se obtine calculand ![]() . Deci
. Deci ![]() .
.
Observatie. Daca
![]() , atunci graficul functiei trece prin origine.
, atunci graficul functiei trece prin origine.
2). Stabilirea coordonatelor varfului.
Dupa cum am vazut mai sus, punctul
de extrem ![]() mai poarta numele
si de varf al
mai poarta numele
si de varf al
functiei de gradul doi. La acest pas vom
calcula ![]() si
si ![]() in functie de
coeficientii functiei de gradul doi dati.
in functie de
coeficientii functiei de gradul doi dati.
3) Axa de simetrie.
Axa de simetrie este o dreapta ce trece
prin varful parabolei si fata de care punctele parabolei sunt
simetrice doua cate doua. Axa de simetrie este paralela cu axa Oy
si are ecuatia : ![]() .
.
4) Tabelul de variatie.
Se determina si se inscriu intr-un tabel de variatie coordonatele unui numar finit de puncte ale curbei.
5) Trasarea graficului.
Exemplu :
Sa se reprezinte grafic functia ![]() ,
, ![]() .
.
Studiem intersectia cu axele de coordonate :
![]() .
. ![]() .
.
Stabilim coordonatele virfului : ![]() .
.
Ecuatia axei de simetrie este : ![]() .
.
Tabelul de variatie :
|
|
|
|
|
|
Graficul :
Pozitia radacinilor ecuatiei de gradul doi fata de un parametru real
Fiind data ecuatia de gradul doi ![]() ,
, ![]() , cu
, cu ![]() (i.e. admite doua
radacini reale
(i.e. admite doua
radacini reale ![]() ) si numarul real
) si numarul real ![]() , ne propunem sa precizam conditiile, astfel
incat :
, ne propunem sa precizam conditiile, astfel
incat :
Notam ![]() si ecuatia
se scrie
si ecuatia
se scrie ![]()
![]()
![]() . Ecuatia
. Ecuatia ![]() are
radacinile
are
radacinile ![]() ,
, ![]() care sunt in
acelasi timp reale cu cele ale ecuatiei initiale
care sunt in
acelasi timp reale cu cele ale ecuatiei initiale ![]() .
.
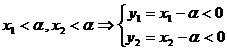 si deci se
pun conditiile ca ecuatia
si deci se
pun conditiile ca ecuatia 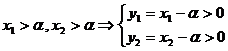 si deci se
pun conditiile ca ecuatia
si deci se
pun conditiile ca ecuatia 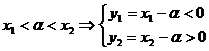 si deci se
pun conditiile ca ecuatia
si deci se
pun conditiile ca ecuatia
Observatie.
Pentru determinarea conditiilor necesare si suficiente de mai sus se
poate utiliza o metoda care sa implice graficul functiei de
gradul doi . Spre exemplu, prima situatie ![]() poate fi
ilustrata grafic prin
poate fi
ilustrata grafic prin 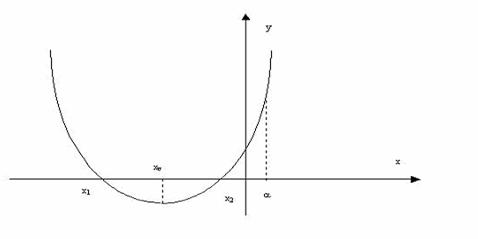
iar conditiile ce se impun sunt :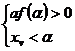 , unde
, unde ![]() este abscisa varfului
(al punctului de extrem al functiei). Conditia
este abscisa varfului
(al punctului de extrem al functiei). Conditia ![]() , apare ca evidenta din moment ce
, apare ca evidenta din moment ce ![]() ,
, ![]() si
si ![]() . Scriind functia de gradul al doilea sub forma
descompusa in factori liniari :
. Scriind functia de gradul al doilea sub forma
descompusa in factori liniari : ![]() , deducem ca
, deducem ca ![]() .
.
In cazul al doilea ![]() ,
, ![]() , conditiile care rezulta prin aceasta
metoda sunt :
, conditiile care rezulta prin aceasta
metoda sunt : 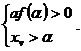 In cel de-al treilea
caz, conditia necesara si suficienta este
In cel de-al treilea
caz, conditia necesara si suficienta este ![]() .
.
Observatie. In cazul in care inegalitatile nu sunt stricte, conditiile se deduc ca mai sus prin una din cele doua metode .
Pozitia radacinilor ecuatiei de gradul doi fata de doua numere reale distincte
Fiind data ecuatia de gradul doi ![]() ,
, ![]() , cu
, cu ![]() (i.e. admite doua
radacini reale
(i.e. admite doua
radacini reale ![]() ) si numerele reale
) si numerele reale ![]() ne propunem sa
stabilim conditiile astfel incat :
ne propunem sa
stabilim conditiile astfel incat :
Efectuam transformarea ![]() si se obtine
o ecuatie de forma
si se obtine
o ecuatie de forma ![]() ale carei
radacini sunt
ale carei
radacini sunt ![]() si
si ![]() . In continuare rationamentul este acelasi ca la
paragraful anterior. De exemplu sa analizam prima situatie :
. In continuare rationamentul este acelasi ca la
paragraful anterior. De exemplu sa analizam prima situatie :
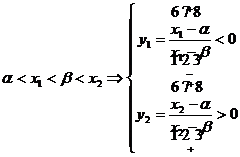 adica
radacinile ecuatiei
adica
radacinile ecuatiei
Observatie. Pentru determinarea conditiilor necesare si suficiente de mai sus, se poate utiliza si o metoda geometrica, nu vom insista asupra ei.
Exercitii propuse
1. Formati ecuatia de gradul al
doilea cand se cunosc ![]() si
si ![]() .
.
2. Sa se aduca la forma canonica urmatoarele functii de gradul doi :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
3. Sa se determine axa de simetrie si varful parabolei asociat functiilor :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
4. Sa se stabileasca maximul sau minimul urmatoarelor functii :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
5. Sa se stabileasca semnul urmatoarelor functii :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
6. Sa se traseze graficul urmatoarelor functii :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
7. Fie ecuatia ![]() ,
, ![]() . Fara a rezolva ecuatia sa se exprime in
functie de
. Fara a rezolva ecuatia sa se exprime in
functie de ![]() expresiile :
expresiile :
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
8. Sa se determine parametrul ![]() astfel incat intre
radacinile ecuatiilor urmatoare sa existe relatia
scrisa in dreptul fiecareia :
astfel incat intre
radacinile ecuatiilor urmatoare sa existe relatia
scrisa in dreptul fiecareia :
9. Sa se gaseasca o
relatie independenta de ![]() intre
radacinile ecuatiei :
intre
radacinile ecuatiei :
![]() .
.
10. Determinati ![]() si
si ![]() reali, astfel incat
ecuatiile
reali, astfel incat
ecuatiile ![]() si
si ![]() sa aiba
aceleasi radacini.
sa aiba
aceleasi radacini.
11. Sa se rezolve inecuatiile :
a)
![]() ;
;
b)
![]() ;
;
c)
![]() ;
;
d) ![]() ;
;
e)
![]() ;
;
f)
![]() .
.
12. Daca ![]() ,
, ![]() sunt
radacinile ecuatiei
sunt
radacinile ecuatiei ![]() , sa se formeze ecuatia de gradul al doilea in
, sa se formeze ecuatia de gradul al doilea in ![]() ale carei
radacini sunt :
ale carei
radacini sunt :
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
13. Sa se rezolve urmatoarele ecuatii :
14. Fie ecuatia ![]() . Sa se determine
. Sa se determine ![]() , astfel incat ambele radacini sa fie mai mici
decat 1.
, astfel incat ambele radacini sa fie mai mici
decat 1.
15. Sa se determine ![]() astfel incat :
astfel incat :
![]() .
.
16. Pentru ce valori ale lui ![]() , multimea :
, multimea :
![]() are doua elemente
.
are doua elemente
.
17. Sa se determine valorile lui ![]() pentru ca ecuatia
pentru ca ecuatia
![]() sa admita o
radacina mai mica decat 1, iar cealalta mai mare decat
2.
sa admita o
radacina mai mica decat 1, iar cealalta mai mare decat
2.
18. Daca ![]() sunt
radacinile ecuatiei
sunt
radacinile ecuatiei ![]() ,
, ![]() , sa se calculeze in functie de
, sa se calculeze in functie de ![]() expresiile :
expresiile :
19. Sa se determine ![]() , astfel incat
, astfel incat ![]() .
.
20. Sa se determine valorile lui ![]() , astfel incat relatiile de mai jos sa fie
satisfacute pentru orice
, astfel incat relatiile de mai jos sa fie
satisfacute pentru orice ![]() :
:
21. Pentru ce valori ale lui ![]() , suma radacinilor ecuatiei
, suma radacinilor ecuatiei ![]() , este minima ?
, este minima ?
22. Gasiti cea mai mica si
cea mai mare valoare a expresiei ![]() , daca numerele reale
, daca numerele reale ![]() verifica
relatia
verifica
relatia ![]() .
.
23. Pentru ce valori ale lui ![]() urmatorul sistem
urmatorul sistem 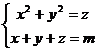 admite solutie
unica ?
admite solutie
unica ?
24. Sa se rezolve ecuatia : ![]() .
.
25. Fie ![]() un numar real
si
un numar real
si ![]() radacinile
ecuatiei :
radacinile
ecuatiei : ![]() .
.
a).
Sa se arate ca ![]() sunt numere reale
pozitive si distincte.
sunt numere reale
pozitive si distincte.
b).
Sa se arate ca ![]() .
.
c).
Sa se calculeze ![]() .
.
d).
Sa se arate ca daca ![]() , in intervalul
, in intervalul ![]() se afla cel mult
un patrat perfect.
se afla cel mult
un patrat perfect.
26. Fie ![]() astfel incat
astfel incat ![]() . Demonstrati ca :
. Demonstrati ca : ![]() .
.
27. Sa se arate ca ecuatia ![]() ,
, ![]() ,
, ![]() impare, nu are
radadcini rationale.
impare, nu are
radadcini rationale.
28. Sa se rezolve ecuatia : ![]() .
.
29. Fie ![]() radacinile
ecuatiei :
radacinile
ecuatiei : ![]() , m fiind un parametru real.
, m fiind un parametru real.
a).
Gasiti o relatie independenta de ![]() intre
intre ![]() si
si ![]() .
.
b).
Determinati intervalul minimal ("cel mai scurt") ce contine pe ![]() si
si ![]() .
.
30. Fie multimile :
![]()
![]() .
.
Cate triunghiuri au toate varfurile in
punctele multimii ![]() ?
?
31. Se considera ecuatiile de gradul doi :
![]() ,
, ![]() .
.
a). Sa se arate ca daca
ecuatiile au o radacina comuna, atunci ![]() sau
sau ![]() .
.
b). Sa se arate ca cel putin una din ecuatiile de mai sus are radacini reale.
32. Sa se rezolve ecuatia : ![]() .
.
33. a).
Daca ![]() si
si ![]() , aratati ca
, aratati ca ![]() .
.
b).
Fie ecuatia : ![]() .
.
i).
Aflati valorile parametrului ![]() astfel incat
ecuatia sa aiba cel putin o radacina
intreaga.
astfel incat
ecuatia sa aiba cel putin o radacina
intreaga.
ii).
Exista valori reale ale lui ![]() astfel incat ambele
radacini sa fie intregi ?
astfel incat ambele
radacini sa fie intregi ?
34. Sa se rezolve ecuatia : ![]() .
.
35. Fie ecuatia : ![]() . Cate solutii sunt in intervalul
. Cate solutii sunt in intervalul ![]() ?
?
36. Sa se rezolve ecuatia : 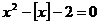 .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 12778
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved