| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
DOCUMENTE SIMILARE |
|||
|
|||
Permutari, Matrice, Determinanti - probleme
1) Fie A=  B=
B= 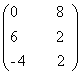 .
Sa se calculeze A+B.
.
Sa se calculeze A+B.
2) Fie A=  B=
B= 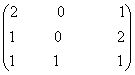 Sa se calculeze
Sa se calculeze
a) A+B; AB; BA
b) A2; B2; A2-B2
3) Daca A= 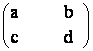
![]() M2(C), atunci a verifica
ecuatia:
M2(C), atunci a verifica
ecuatia:
x2 - (a+d)x +(ad-bc)I2 =0
4) Fie A= 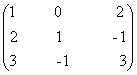
![]() M3(Q). Daca f(x) = x2+3x+I3,
sa se calculeze f(A).
M3(Q). Daca f(x) = x2+3x+I3,
sa se calculeze f(A).
5) Fie A= 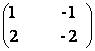
![]() M2(Q). Sa se determine toate
matricile X
M2(Q). Sa se determine toate
matricile X![]() M2(Q) astfel incat AX=XA.
M2(Q) astfel incat AX=XA.
6) Sa se determine x,z,z,u,v,w daca se cunoaste ca avem egalitatea:
2![]() +
3
+
3![]() =
=
![]()
7) Sa se determine matricea X din ecuatia:
3X + 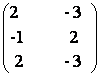 =
2
=
2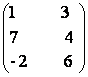 +
+

8) Sa se determine x si y, daca avem:
x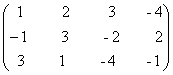 +y
+y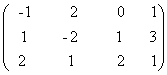 =
=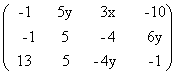
9)
Sa se determine valorile lui x![]() R pentru care avem:
R pentru care avem:
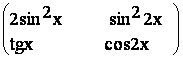 =
= 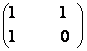
10) Sa se rezolve ecuatia:
X2 = 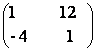
unde Xeste o matrice patrata de ordinul 2 cu elemente numere reale.
11) Sa se calculeze
suma: 
12) Daca w este o radacina a ecuatiei x2+x+1=0, sa se caluleze suma:

13) Sa se gaseasca matriea X, in fiecare din cazurile:
a)  x
=
x
= 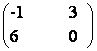
b) 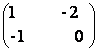 x
=
x
= 
c)  x
=
x
=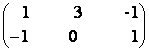
d)  x
=
x
= ![]()
14) Se considera
egalitatea de matrice 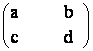 2
=
2
= 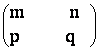 .
Sa se arate ca daca numerele a, b, c d sunt in progresie
aritmetica, atunci si numerele n-m, p-n, q-p au aceeasi
proprietate.
.
Sa se arate ca daca numerele a, b, c d sunt in progresie
aritmetica, atunci si numerele n-m, p-n, q-p au aceeasi
proprietate.
15) Sa se afle matricea
X![]() M2(R) daca:
M2(R) daca:
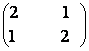 x - x
x - x =
=
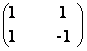
15) Fie
A= 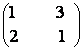 si X=
si X= 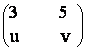
a) Sa se determine u si v astfel incat AX=XA.
16)
Fiind date matricile A=  B=
B= 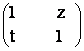 A,B
A,B![]() M2(R)
M2(R)
Se cere: a) Sa se calculeze patratul sumei matriceale A+B.
b) Sa se rezolve sistemul in x, y, z, t rezultat din egalitatea matriceala:
A.B = 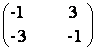 .
.
17) Fie G multimea matricilor din M3(R) de forma:
Mab = 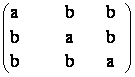
a) Sa se arate ca oricare ar fi doua matrici din G, Ma1b1 si Ma2b2 produsul lor este tot o matrice din G.
b) Sa se arate ca Ma1b1 .Ma2b2 = Ma2b2. Ma1b1.
c) Sa se
stabileasca daca I![]() G.
G.
18) Fie A, B, C ![]() M3(R)
M3(R)
A = 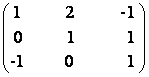 B=
B= 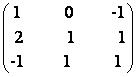 C=
C= 
a) Sa se calculeze (A+B+C)n,
n![]() N
N
b) Sa se
gaseasca x, y, z ![]() M3(R) astfel incat:
M3(R) astfel incat:
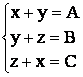
19) Sa se determine
matricea x ![]() M3(N) astfel incat (1 2 4)x
=(3 1 2)
M3(N) astfel incat (1 2 4)x
=(3 1 2)
20) Sa se rezolve
ecuatia X2 = 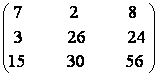 stiind
ca xij =0 pentru i+j = 4 (i,j = 1, 2, 3), xij
elementele matricei X.
stiind
ca xij =0 pentru i+j = 4 (i,j = 1, 2, 3), xij
elementele matricei X.
21) Fie matricea X= 
![]() M2(R)
M2(R)
a) Sa se arate ca X verifica relatia X2-2xX+ x2I=0.
b) Sa se calculeze Xn
si sa se arate ca pentru nr. n![]() N este adevarata :
N este adevarata :
nXn+1-(n+1)xXn + xn+1I2 =0
c) Sa se gaseasca x si y, astfel incat Xn.t(Xn) = I2.
22) a) Se considera
matricea  .
Sa se determine toate matricele X, astfel incat A2X = XA2
si sa arate ca nu exista nici o matrice Y astfel incat A2Y-
YA2 =
.
Sa se determine toate matricele X, astfel incat A2X = XA2
si sa arate ca nu exista nici o matrice Y astfel incat A2Y-
YA2 =  .
.
23) Se considera
matricea A = 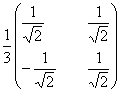 .
Sa se calculeze An, n
.
Sa se calculeze An, n![]() N si limita fiecarui
element al lui An pentru n
N si limita fiecarui
element al lui An pentru n![]() .
.
24) Fie M multimea
matricilor patrate de ordin 2 de forma 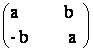 unde a,b
unde a,b![]() R. Definim functia f: C
R. Definim functia f: C![]() , f(a+b.i) =
, f(a+b.i) = 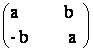 .
Sa se arate ca:
.
Sa se arate ca:
a) f este bijectiva;
b) oricare ar fi z,z'![]() C au loc
egalitatile
C au loc
egalitatile
f(z+z') = f(z) + f(z')
f(zz') = f(z)f(z')
25) Fie matricea A = 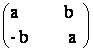 astfel
incat 0
astfel
incat 0 ![]() <1.
<1.
a) Sa se arate ca
matricea An este de forma 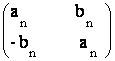 .
.
b) Sa se demonstreze ca sirurile (an) si (bn) sunt convergente si au limita zero.
26) Sa notam cu M multimea tuturor matricelor de tipul (m,n) in care toate elementele sunt nx+1 sau -1 si astfel incat produsul numerelor din fiecare linie si din fiecare coloana sa fie -1. Sa se calculeze numarul elementelor multimii M.
27) Sa se calculeze suma
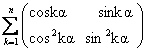
28) Fie matricile A= 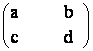 si
B=
si
B= 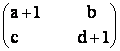 cu
ad = bc.
cu
ad = bc.
a) Sa se arate ca
exista un numar real r, astfel incat pentru orice K![]() N sa avem Ak
= rk-1A.
N sa avem Ak
= rk-1A.
b) Folosind egalitatea B =
I+A. Sa se calculeze Bn, n![]() N
N
c) Sa se studieze
convergenta sirurilor xn, yn care verifica
egalitatile x1 =p, y1=q, ![]() =
B
=
B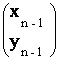 .
.
29) Fie M multimea matricilor din M2(R) de forma:
A![]() =
=
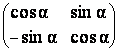
a) Sa se arate ca
oricare ar fi A![]() ,
A
,
A![]()
![]() M si A
M si A![]() .
A
.
A![]() A
A![]() .
A
.
A![]() .
.
b) Sa se calculeze ![]()
![]() R daca (A
R daca (A![]() )2
= (A
)2
= (A![]() )
= Ao.
)
= Ao.
30) Fie matricile A,B![]() M3(R) unde
M3(R) unde
A = 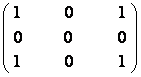 si
B=
si
B= 
a) Sa se calculeze: An; B2n si B2n+1
b) Sa se arate ca An+
B2n + B2n+1 = 2n
31) Fie matricea A =  .
Sa se calculeze An, n
.
Sa se calculeze An, n![]() N
N
32) Fie matricea A =  .
Sa se calculeze An, n
.
Sa se calculeze An, n![]() N
N
33) Fie
matricea M![]() M3(R),
M =
M3(R),
M = 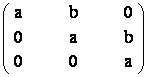 .
Sa se calculeze Mn.
.
Sa se calculeze Mn.
34) Sa se calculeze sistemele matriceale:
a)  b)
b)
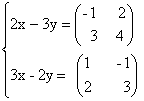
35) a) 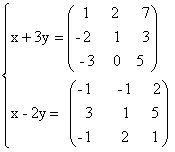 b)
b)
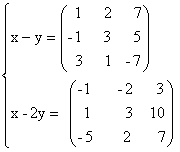
36) Sa se rezolve sistemele:
a) 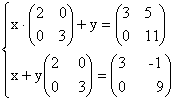
b) 
37)
Sa se determine matricile X de forma 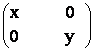 care au proprietatea XA =
AX, unde a) A =
care au proprietatea XA =
AX, unde a) A = 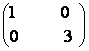 b) B=
b) B= 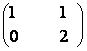 .
.
38) Sa se rezolve in M![]() M2(R)
ecuatiile matriciale:
M2(R)
ecuatiile matriciale:
a) ![]() b)
b) ![]()
39) X2
=  , vezi exercitiul 3.
, vezi exercitiul 3.
40) a) x4 =  b) x4 =
b) x4 = 
41) Sa se rezolve
sistemul  stiind ca X este inversabila.
stiind ca X este inversabila.
42) Sa se rezolve sistemul
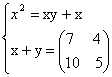
43) Sa se rezolve sistemul
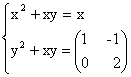 stiind ca X este
matrice inversabila.
stiind ca X este
matrice inversabila.
44)
Sa se determine puterea n a matricelor A![]() M2(R)
M2(R)
a) A = 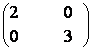 b) A =
b) A = 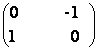
45) Sa se determine
puterea n a matricelor A![]() M2(R)
M2(R)
a) A =  =
= 
b)  =
= 
46) Sa se determine
puterea n a matricelor A![]() M2(R)
M2(R)
a) A = 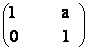
47) Sa se determine
puterea n a matricelor A![]() M3(R)
M3(R)
A = 
48) Sa se determine
puterea n a matricelor A![]() M3(R)
M3(R)
A = 
49) Fie A, B, C A![]() M3(C) astfel
incat A = BC, B = CA, C = AB. Sa se arate ca: A2 = B2
= C2.
M3(C) astfel
incat A = BC, B = CA, C = AB. Sa se arate ca: A2 = B2
= C2.
50) Fie matricea A cu proprietatea A2 = A. Sa se demonstreze relatia:
(2A-I)4 = I.
51) Fie
in M2(R) egalitatea matriciala  =
= 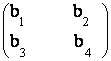 .
Sa se arate ca daca a1, a2, a3,
a4 sunt in progresie aritmetica, atunci b2 - b1,
b3 - b2, b4 - b3 sunt tot in
progresie aritmetica.
.
Sa se arate ca daca a1, a2, a3,
a4 sunt in progresie aritmetica, atunci b2 - b1,
b3 - b2, b4 - b3 sunt tot in
progresie aritmetica.
52) Se considera
matricea A =  .
Sa se calculeze An si
.
Sa se calculeze An si
B = ![]() .
.
53) Fie matricile A =  B =
B = 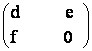 ,
a,b, c,d
,
a,b, c,d ![]() R. Sa se demonstreze
ca daca A+B = AB atunci AB = BA.
R. Sa se demonstreze
ca daca A+B = AB atunci AB = BA.
54) Se
considera matricea Aa,b = 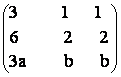 , B=
, B= ![]()
![]() R /
determinantul
R /
determinantul ![]() nu
depinde de x,
nu
depinde de x, ![]()
![]() Rx R*
Rx R*![]() ,
,
![]() =
numarul elementelor lui B, C =
=
numarul elementelor lui B, C = ![]() ,
(a,b)
,
(a,b) ![]() B,
(x,y), Rx R*
B,
(x,y), Rx R*![]()
55) Fie
M = ![]() A
A![]() M2(R)/ A =
M2(R)/ A = 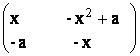 , x
, x ![]() R, det.A =1
R, det.A =1![]() ,
,
B![]() M.
Daca K =
M.
Daca K = ![]() A
A![]() M2(R)/ d
M2(R)/ d![]() det.A
det.A
![]() 0
si det.(A+det.A*) =0
0
si det.(A+det.A*) =0![]() atunci:
atunci:
I a) B
= B-1; b) B+B* ![]() 0,
c) det.(B-B*) = 4; d) B.B* =0, e) B-B* =I.
0,
c) det.(B-B*) = 4; d) B.B* =0, e) B-B* =I.
II a) d =1; b) d=2; c) d=-1; d) d= 3; e) d= -2.
56) Fie M2(R),
A = 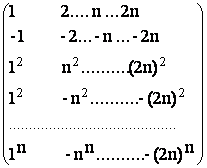
Pentru o matrice B![]() Mm(C),
m
Mm(C),
m![]() N,
m
N,
m![]() 2
fie
2
fie ![]() (B)numarul
minorilor nenuli ai lui B.
(B)numarul
minorilor nenuli ai lui B.
Atunci
I) ![]() (I2n)
= 22n - 1; b)
(I2n)
= 22n - 1; b) ![]() (I2n)
= 22n; c)
(I2n)
= 22n; c) ![]() (I2n)
= 22n + 1;
(I2n)
= 22n + 1; ![]() (I2n)
= 22n-1; e)
(I2n)
= 22n-1; e) ![]() (I2n)
=(2n)!
(I2n)
=(2n)!
II) a) ![]()
![]() 0 b)
0 b) ![]() (A)
= 4n2; c)
(A)
= 4n2; c) ![]() (A)
(A)
![]()
![]() (tA)
d) rang A = n+1; e)
(tA)
d) rang A = n+1; e) ![]() (A)
= C3n2n+2n2-1.
(A)
= C3n2n+2n2-1.
57) Fie M = ![]() Ay
Ay![]() M3(R) Ay =
M3(R) Ay = 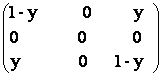 ,
y
,
y![]() D
D ![]() R
R![]() .
Daca (Mi) este un grup cu elemet neutru E, unde "."
este inmultirea matricelor din M3(R)
si S=
.
Daca (Mi) este un grup cu elemet neutru E, unde "."
este inmultirea matricelor din M3(R)
si S= ![]() Ay
Ay![]() M Ay2A1
= E A / simetricul lui A in grupul (M1
M Ay2A1
= E A / simetricul lui A in grupul (M1 ![]() atunci:
atunci:
I) a) D=R;
b) D=R ![]() c) D= R*; d) D=R
c) D= R*; d) D=R ![]() ;
e)
;
e) ![]() Ay
Ay![]() M inversabila.
M inversabila.
II) a) S ![]()
![]() ; b) S=
; b) S= ![]() ;
c) S=
;
c) S= ![]() ;
d) S=
;
d) S= ![]() ;
e)
;
e) ![]() .
.
58) Fie X= 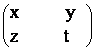
![]() M2(R) astfel
incat X3 =
M2(R) astfel
incat X3 = 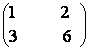 . Daca T=t3
si S= x+y+z+t atunci
. Daca T=t3
si S= x+y+z+t atunci
I) a) T=1; b) T = ![]() ; c) T =
; c) T = ![]() ;
d) T= 27; e) T= 36.
;
d) T= 27; e) T= 36.
II) a) S=2; b) S= ![]() ; c) S =
; c) S = ![]() ;
d) S=12; e) S=
;
d) S=12; e) S= ![]() .
.
59)
Fie inelul (A, +, .) unde A= ![]() x(a,b,c,d)
x(a,b,c,d)
![]() M3(R) x(a,b,c,d)
=
M3(R) x(a,b,c,d)
=  a,b,c,d
a,b,c,d![]() R
R![]() . Fie B
=
. Fie B
= ![]() (a,b)
(a,b)![]() Z*xZ/ b.X(a,b,0,1)
+ aX(a, b, 1, 0) =X(b,
a+16, a, b)
Z*xZ/ b.X(a,b,0,1)
+ aX(a, b, 1, 0) =X(b,
a+16, a, b) ![]() ,
C=
,
C= ![]() (b,d)
(b,d) ![]() R2 / X-1
(1,b,0,d) . X (-1,b,0,d) = X(-1, b2, -8, d2)
R2 / X-1
(1,b,0,d) . X (-1,b,0,d) = X(-1, b2, -8, d2) ![]()
S = ![]() ;
T=
;
T= ![]() atunci
atunci
I) a) S = -4; b) S =-3; c) S = -2; d) S = -1; e) S =0.
II) a) T = S; b) T = 4 S; c) T = 2S; d) T = -2s; e) T = -S.
60) Fie matricea A =  . Sa se calculeze An
. Sa se calculeze An
61) Fie matricea A =  .
Sa se calculeze
.
Sa se calculeze ![]()
62) Fie A o matrice de tipul (4,3) avand elemente numere naturale.
Sa se determine aceasta matrice, astfel incat A ![]() =
=
![]() .
.
63) Sa se determine matricile A![]() M2(R) astfel
incat A2+A+I =0. Sa se arate ca A este inversabila
si sa se afle inversa sa.
M2(R) astfel
incat A2+A+I =0. Sa se arate ca A este inversabila
si sa se afle inversa sa.
64) Fie (A,B) matrici de ordinul n![]() 2
astfel incat AB =BA. Sa se arate ca:
2
astfel incat AB =BA. Sa se arate ca:
a) AkBl = BlAk
oricare K,l![]() N
N
b) (A+B)m = ![]() oricare m
oricare m![]() N
N
65) Fie A = 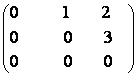 .
Sa se calculeze (I+A)n, unde n
.
Sa se calculeze (I+A)n, unde n![]() N
N
66) Pentru orice matrice A = (aij)![]() matricea
Tr (A) =
matricea
Tr (A) = ![]() , Tr (A) se numeste
urma matricei A. Sa se arate ca
, Tr (A) se numeste
urma matricei A. Sa se arate ca
1) Tr(A+B) = Tr(A) + Tr(B)
2) Tr( ![]() A)
=
A)
= ![]() Tr(A)
Tr(A)
3) Tr(AB) = Tr(BA)
4) Tr(UAU-1) = TrA
67) Determinati matricele A![]() M2(R), A =
M2(R), A = 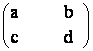 care au proprietatea
ca: An =
care au proprietatea
ca: An =  oricare
ar fi n
oricare
ar fi n![]() N n
N n![]() 2.
2.
68) Determinati x,y![]() R astfel
incat A2+A =aI, unde A =
R astfel
incat A2+A =aI, unde A =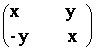
![]() M2(R)
M2(R)
iar a![]() R.
Discutie.
R.
Discutie.
69) Fie ![]() =
=
![]() si A =
si A = 
![]() M3(C).
Calculati An
M3(C).
Calculati An
70) Fie A,B ![]() M2(R) astfel
incat A+B = AB. Aratati ca pentru K
M2(R) astfel
incat A+B = AB. Aratati ca pentru K![]() N, K
N, K![]() 2,
urmatoarele functii sunt echivalente:
2,
urmatoarele functii sunt echivalente:
a) A+B+B + . + BK-1 =0 B) Bk = 0.
71) Fie A![]() Mn(C) o
matrice cu proprietatea ca exista K
Mn(C) o
matrice cu proprietatea ca exista K![]() N* astfel
incat AK=0.
Demonstrati ca matricea I-A este inversabila.
N* astfel
incat AK=0.
Demonstrati ca matricea I-A este inversabila.
72) Fie A,B ![]() M2(C) astfel
incat A = A2 si A+B =I.
M2(C) astfel
incat A = A2 si A+B =I.
a) Demonstrati ca exista K![]() N astfel
incat (A-A2)k = 0
N astfel
incat (A-A2)k = 0
b) Aratati ca o matrice I+AB este inversabila.
73) Reduceti la forma esalon matricile:
a)
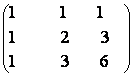
![]()
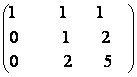
![]()
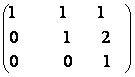
b) 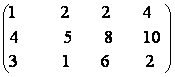
![]()

![]()

74) Determinati
numarul liderilor formei esalon pentru diferite valori ale lui ![]()
![]() R in
urmatoarele situatii:
R in
urmatoarele situatii:
a)
![]()
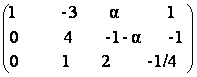
![]()
 daca 2 +
daca 2 + ![]() =0
atunci avem 3 lideri esalon, altfel 2 lideri.
=0
atunci avem 3 lideri esalon, altfel 2 lideri.
b)
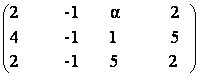
75) Stabiliti, cu ajutorul transformarilor elementare, daca urmatoarele matrici sunt inversabile si in caz afirmativ calculati inversele.
76) Scrieti ca un produs de matrice elementare de tip I, urmatoarele matrice:
a) 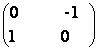 ,
, 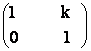
 =
=
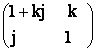
![]()

![]()
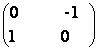 =
=

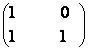
b) 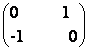
77) Fie A = 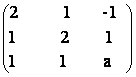
![]() M3(R).
M3(R).
a) Determinati a astfel incat A sa fie inversabila.
b)
Pentru
a=2 determinati A si rezolvati ecuatia AX = 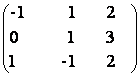
78) Fie A =  . Sa se arate ca pentru orice n
. Sa se arate ca pentru orice n![]() 2, n
2, n![]() N*
exista matricele xn,
yn, zn
N*
exista matricele xn,
yn, zn ![]() M2(R) distincte si nenule astfel incat An =
Xnn+ Ynn+ Znn.
M2(R) distincte si nenule astfel incat An =
Xnn+ Ynn+ Znn.
79) Fie r, ![]()
![]() R, r
R, r![]() 0
si A =
0
si A = 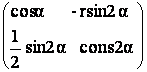 An =
An = 
80) Fie A![]() Mn(R)
cu proprietatea ca A.X = X.A,
pentru orice
Mn(R)
cu proprietatea ca A.X = X.A,
pentru orice
X![]() Mn(R).
Demonstrati ca exista
Mn(R).
Demonstrati ca exista ![]()
![]() R astfel incat A =
R astfel incat A =
![]() I.
I.
81) Consideram multimea:
M = ![]() A = (aij)
A = (aij)![]() / aij>0
/ aij>0 ![]() i,j,
i,j,
![]()
![]() i,j
i,j![]() Aratati ca:
Aratati ca:
a) Daca A,B![]() M, atunci A.X
M, atunci A.X ![]() M.
M.
b)
Daca A![]() M,
atunci
M,
atunci ![]()
![]()
![]()
82) Fie A![]() Mn(R cu proprietatea A2
= A. Demonstrati ca (I-A)2 = I-A si A(I-A) = (I-A)
.A.
Mn(R cu proprietatea A2
= A. Demonstrati ca (I-A)2 = I-A si A(I-A) = (I-A)
.A.
83) Fie A,B![]() M2(R) matrice inversabile, iar M =
M2(R) matrice inversabile, iar M = 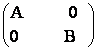
![]() M4(R).
Demonstrati ca matricea M este inversabila si ca M-1
=
M4(R).
Demonstrati ca matricea M este inversabila si ca M-1
=  .
.
84) Fie M = ![]() N
N ![]() Mn(C) /
Mn(C) / ![]() K
K![]() N astfel incat Nk =0
N astfel incat Nk =0![]() multimea matricilor nulpotente. Pentru N
multimea matricilor nulpotente. Pentru N![]() M
se numeste coeficientul de nulpotenta al matriceiN, cel mai mic
numar natural p cu proprietatea Np =0. Definim eN =
I+N+
M
se numeste coeficientul de nulpotenta al matriceiN, cel mai mic
numar natural p cu proprietatea Np =0. Definim eN =
I+N+![]() +
.+
+
.+ ![]() daca
N
daca
N![]() M
si are coeficientul de nulpotenta p.
M
si are coeficientul de nulpotenta p.
Demonstrati ca:
a) ![]() +
+![]() =
= ![]() .
.![]() pentru N1, N2
pentru N1, N2 ![]() M.
M.
b) eN este matrice inversabila si (eN)
= e-N pentru N ![]() M.
M.
85) Fie Hk = (tij)![]() o matrice de ordinul n definita astfel:
o matrice de ordinul n definita astfel:
tij = ![]() unde
K este un numar fixat din multimea:
unde
K este un numar fixat din multimea:
![]() -(n-1), -(n-2), ., -1, 1, 2, ., (n-1)
-(n-1), -(n-2), ., -1, 1, 2, ., (n-1) ![]() .
Demonstrati ca H1K = HK, H-1K
= H-K daca 1
.
Demonstrati ca H1K = HK, H-1K
= H-K daca 1![]() k
k![]() n
si H1K = H-1K = 0 pentru K
n
si H1K = H-1K = 0 pentru K![]() n.
n.
86) Fie A![]() Mn(C) si tA transpusa sa.
Mn(C) si tA transpusa sa.
a) Demonstrati ca matricea B= A. tA este o matrice sometrica (B =. tB).
b) Daca matricea A este inversabila atunci si A-1 este simetrica.
c) Daca matricea A este antisimetrica (tA = -A) si inversabila, atunci si A-1 este antisimetrica.
87) Demonstrati ca produsul a doua matrice simetrice ese o matrice simetrica daca si numai daca cele doua matrici comuta.
88) Demonstrati ca produsul a doua matrici antisimetrice este o matrice simetrica daca si numai daca cele doua matrici comuta.
89) Demonstrati ca produsul a doua matrici A, B antisimetrice este o matrice antisimetrica daca si numai daca AB = -BA.
90) Fie a, b, c indicii lui f = X3 + X + 1 ![]() C[X].
C[X].
a)
Calculati 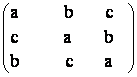
b) Calculati a3 + b3 +c3;
c) Calculati P = 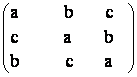
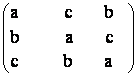
d) Sa se arate ca an + bn +cn![]() Z si sa se calculeze a10 + b10 +c10.
Z si sa se calculeze a10 + b10 +c10.
91) In M2![]() (R), I2 =
(R), I2 = ![]() ,
A =
,
A = ![]() si
submultimea G =
si
submultimea G = ![]() X(a)/a
X(a)/a![]() R si X(a) = I + aA
R si X(a) = I + aA![]() .
a) Sa se calculeze A2; b) Sa se arate I2
.
a) Sa se calculeze A2; b) Sa se arate I2 ![]() G;
c)Sa se demonstreze ca X(a) .X(b) = X(a+b+2ab),
G;
c)Sa se demonstreze ca X(a) .X(b) = X(a+b+2ab), ![]() a,
b
a,
b ![]() (R); d) Sa se arate ca daca a
(R); d) Sa se arate ca daca a![]()
![]() atunci
X(a) .X(
atunci
X(a) .X(![]() )
= I2; e) Sa se demonstreze ca
)
= I2; e) Sa se demonstreze ca ![]() t
t![]() Z X(
Z X(![]() )
.X(
)
.X(![]() ).X(
).X(![]() )
)![]() X(t)
X(t)
92) Se considera A = 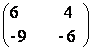 .
.
a) Sa se calculeze det.A si rang A.
b) Calculati A2; c) Sa se determine B = A + 22A2 + . + 20012A2001.
93) Fie A = 
a) Calculati A2;
b) Sa se calculeze det.A si rang A.
c) Pentru x![]() C definim B(x) = I + XA+X2A2 + . + X2001A2001.
Calculati B(x);
C definim B(x) = I + XA+X2A2 + . + X2001A2001.
Calculati B(x);
d) Sa se arate ca B(x) este inversabila
pentru ![]() X
X ![]() C
C
94) Fie A = 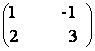 .
.
a) Calculati A2 si A3.
b) Calculati det. An, ![]() n = 2, 3, 10
n = 2, 3, 10![]() .
.
c) Verificati daca A2 = 4A - 5I.
d) Aratati ca An+1 = 4An
- 5 An-1, n![]()
e) Demonstrati ca An ![]() In,
In,
![]() n
n![]() N
N
95) In M2![]() (R) A =
(R) A =  si
B =
si
B =  .
.
a) Sa se arate ca E este inversabila si sa se calculeze A-1;
b) Calculati C = ![]() ;
;
c) Calculati Cn, Bn , n![]()
96) In M2![]() (R) A =
(R) A = 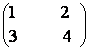 ,
B =
,
B = 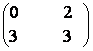 ,
C =
,
C =  .
.
a) Aratati ca AB = BA, AC![]() CA;
CA;
b) Calculati Cn.
97) In M2![]() (C) se considera submultimea H =
(C) se considera submultimea H = 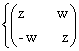 /
z, w
/
z, w![]() C
C![]()
a) Sa se verifice I![]() H;
b) A,B
H;
b) A,B ![]() H
H ![]() AB
AB![]() H;
c) Sa se demonstreze ca daca A
H;
c) Sa se demonstreze ca daca A ![]() H si det.A =0 atunci A =0; d) Sa se
gaseasca A,B
H si det.A =0 atunci A =0; d) Sa se
gaseasca A,B![]() H astfel incat AB
H astfel incat AB![]() BA.
BA.
98) In M2![]() (C) se considera submultimea G =
(C) se considera submultimea G = 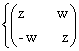 /
z, w
/
z, w![]() C
C![]()
a) Sa se verifice A![]() G
atunci rang A <2
G
atunci rang A <2 ![]() A =0.
A =0.
b) Sa se determine X![]() G
astfel incat XA
G
astfel incat XA![]() AX
unde A =
AX
unde A = 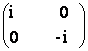 .
.
c) Daca A![]() G,
A
G,
A![]() 0
atunci exista A-1 si A-1
0
atunci exista A-1 si A-1![]() G.
G.
99) In M3![]() (C), A =
(C), A =  si functia f: M3 (C)
si functia f: M3 (C) ![]() M3 (C) f(x)= X3.
M3 (C) f(x)= X3.
a) Calculati det.A, rang A.
b) Calculati A2 si A3.
c) Sa se arate ca daca Y![]() M3 (C) si YA = AY, atunci
M3 (C) si YA = AY, atunci ![]() a,
b, c
a,
b, c ![]() C astfel incat Y
=
C astfel incat Y
=  .
.
d) Sa se arate ca, daca Z =  a, b, c
a, b, c ![]() C si det. Z
=0 atunci Z3 = O3.
C si det. Z
=0 atunci Z3 = O3.
100) In M2![]() (R) A =
(R) A = 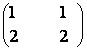 ,
I2 =
,
I2 = 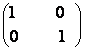 ,
G =
,
G = ![]() X(a)/ si
X(a) = aA + I2, a
X(a)/ si
X(a) = aA + I2, a![]() R
R![]()
a) Sa se verifice I2![]() G;
G;
b) Sa se arate ca A2 = 3A;
c) Sa se arate ca X(a) ![]() X(b) = X(3ab+a+b)
X(b) = X(3ab+a+b) ![]() a,b
a,b ![]() R
R
d) Sa se calculeze det.A, rang A;
e) Sa se determine a![]() R pentru care X
R pentru care X![]() X
X![]() .
X
.
X ![]() X
X![]() =
X(a).
=
X(a).
101) Se
considera A = 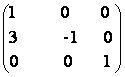 B=
B= 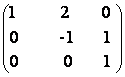 .
.
a) Caclulati A![]() B
si B
B
si B![]() A;
A;
b) Det.A si rang A;
c) Verificati daca A2 = B2 =I;
d) Exista A-1? Atunci sa se determine;
e) Sa se calculeze determinantul lui X = A + A2+ A3. + A2002;
f)
Sa se arate ca (A![]() B)n
B)n
![]() I
I
![]() n.
n.
A![]() M3 (C), A =
M3 (C), A = 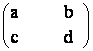 .
.
a) Determinati matricea X ![]() M2 (C) stiind ca X = A2 - (a+d)A+(ad-bc)I;
M2 (C) stiind ca X = A2 - (a+d)A+(ad-bc)I;
b) Calculati A2002 pentru A = 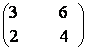 ;
;
c) Daca ![]() A
=0,
A
=0, ![]()
![]() R atunci
R atunci ![]() =0 sau A=0;
=0 sau A=0;
d) Aratati ca daca ![]() K,
k
K,
k![]() 3
astfel incat Ak = 0 atunci A2 =0;
3
astfel incat Ak = 0 atunci A2 =0;
e) Aratati ca pentru ![]() A,B,C
A,B,C
![]() M2 (C) exista egalitatea (AB-BA)2
M2 (C) exista egalitatea (AB-BA)2![]() C
= C(AB-BA)2.
C
= C(AB-BA)2.
103) Fie X = ![]() ,
Y = (1 1 -1), A =
,
Y = (1 1 -1), A =  .
Pentru a
.
Pentru a![]() R definim B = aA + I3.
R definim B = aA + I3.
a) Calculati A - XY;
b) Calculati A2;
c) Sa se arate ca 2B-B2 =0;
d) Sa se arate ca nu exista A-1;
e) Sa se demonstreze ca Bn = I+a![]() n
n![]() A.
A.
104) Fie X = ![]() ,
Y= (-1 1 2 -2), A =
,
Y= (-1 1 2 -2), A = 
a) Calculati XY-A; b) det.A, rang A; c) Calculati A2.
105) Fie numerele reale distincte a, b, c, d, f, g : R![]() R,
R,
f(x) =(x-a)(x-b)(x-c)(x-d), g(x) = x3+x+1 si det.![]() =
= 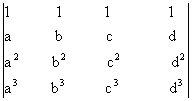 .
.
a) Verificati  =
(y-z)(z-x)x-y),
=
(y-z)(z-x)x-y), ![]() x,y,z
x,y,z![]() R
R
b) Aratati ca ![]() = (b-a)(c-a)(d-a)(c-b)(d-b)(d-c);
= (b-a)(c-a)(d-a)(c-b)(d-b)(d-c);
c) Verificati daca A = ![]() ,
unde A =
,
unde A =  ;
;
d) Verificati daca f'(a) = (a-b)(a-c)(a-d);
e) Dezvoltati A dupa ultima linie si aratati ca
![]() +
+ ![]() +
+
![]() +
+
![]() =
1.
=
1.
106) Fie matricea
A = 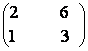 .
.
a) verificati A2 = 5A;
b) Aratati ca An= 5n-1A ![]() n;
n;
c) Aratati ca matricea A- A2 + A3 -.+(-1)99A100 are toate elementele strict negative.
107) Fie d=  a, b, c
a, b, c ![]() C
C
a) Dezvoltand d aratati ca d= a3 + b3+c3+3abc;
b) Folosind proprietatile determinantilor aratati d= (a+b+c)(a2+b2+c2-ab-ac-bc);
c) Aratati ca a2+b2+c2-ab-ac-bc=
![]() ;
;
d) Rezolvati 8X+27X+125X =3![]() 30X.
30X.
108) In M2(Z5), A = 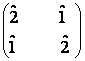 .
.
a) Calculati det.A;
b) Calculati A2; A4;
c) Determinati B![]() M2(Z5
M2(Z5
d) Calculati A2001.
109) In M2 (R), A= 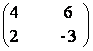 si
G =
si
G = ![]() X(a)/ a
X(a)/ a![]() R si X(a) = aA + I2
R si X(a) = aA + I2![]() .
.
a) Calculati det.A, rang A, aratati ca I![]() G;
G;
b) Aratati ca X(a)X(b) = X(a+b+ab) ![]() a,b;
a,b;
c) Aratati ca X(1)..X(2001) = X(2002!-1).
110) Fie M 2,1(Z) si A= 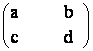
![]() M 2(Z
M 2(Z
Definim f: M 2,1(Z) ![]() M
2,1(Z) f(x) = Ax, unde x=
M
2,1(Z) f(x) = Ax, unde x= ![]()
a) Verificati daca f(x+y) = f(x) + f(y);
b) f(![]() x)
=
x)
= ![]() f(x),
f(x),
![]()
![]() Z
Z
c) Aratati daca det.A![]() 0
0
![]() f
injectiva, det.A
f
injectiva, det.A ![]()
![]()
![]()
![]() f
bijectiva.
f
bijectiva.
111) Fie A=  B=
B=  C=
aA+bB, a,b
C=
aA+bB, a,b![]() R.
R.
a) Calculati det.A, rang A;
b) Demonstrati ca rang(aA+bB) = 3![]() ab
ab![]() 0;
0;
c) Aratati ca atunci ![]() n
n![]() N avem Xn = tn-1X;
N avem Xn = tn-1X;
d) Determinati Cn , ![]() n
n![]() N
N
112) Fie matricea
A = 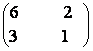 ,
A
,
A![]() M 2(R
M 2(R
i) Sa se
determine multimea matricilor M = ![]() X/det.X =0, det.(A+X) = 0
X/det.X =0, det.(A+X) = 0![]() .
.
ii) Daca X1,
X2 ![]() M
sa se verifice daca suma X1+X2
M
sa se verifice daca suma X1+X2 ![]() M.
M.
113) Fie matricea A = 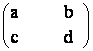 ,
A
,
A ![]() M
2(R)cu a
M
2(R)cu a![]() d,
b
d,
b![]() c,
b
c,
b![]() 0,
c
0,
c![]() 0.
Notam An =
0.
Notam An = 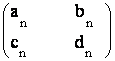 .
Sa se demonstreze ca
.
Sa se demonstreze ca ![]() =
=
![]() =
=
![]() ,
stiind ca An
,
stiind ca An![]() A = A
A = A ![]() An.
An.
Rang matrici
1) Sa se determine rangul matricei A = 
![]() M 4,5(R
M 4,5(R
2)
Fie matricile A![]() M
3,4(R), B M 3(R
M
3,4(R), B M 3(R
A = 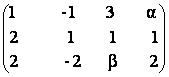 B =
B = 
Se cere:
a) Sa se calculeze rangul matricei A;
b) Sa se determine ![]() ,
,
![]()
![]() R astfel incat
rang A = rang B.
R astfel incat
rang A = rang B.
3) Se da
matricea A![]() M
3(R), A =
M
3(R), A =  .
Se cere:
.
Se cere:
a) Sa se determine valorile lui ![]() pentru care A este nesingulara.
pentru care A este nesingulara.
b) Pentru ![]() = -3 sa se gaseasca inversa
matricei A.
= -3 sa se gaseasca inversa
matricei A.
4) Sa se rezolve ecuatia matriceala AXB = C unde:
A = 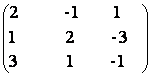 B =
B = 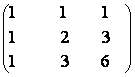 C=
C= 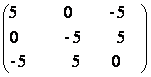
5) Sa se calculeze rangul matricelor urmatoare, pentru diferite valori ale lui ![]() :
:
a)  ;
b)
;
b) 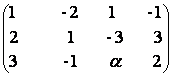
6) Sa se determine rangul urmatoarelor matrici,
prin aducere la forma canonica diagonala, pentru diferite valori ale
lui ![]() ,
,![]() ,
,![]() ,
,![]()
![]() R
R
a) 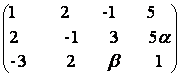 b)
b)
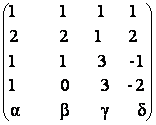
7) Se considera matricile:
A = 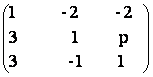 B =
B = 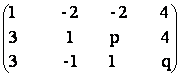
Sa se afle numerele p si q, astfel incat cele doua matrici sa aiba acelasi rang.
8) Sa se calculeze rangul matricei A = 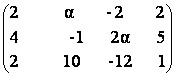 .
Discutie dupa
.
Discutie dupa ![]() .
.
9) Fie A = 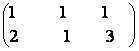 B =
B = 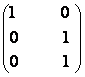 .
Se cere:
.
Se cere:
a) Sa se gaseasca rangul matricelor A si B.
b) Sa se calculeze AB.
c) Sa se gaseasca rangul matricei AB.
d) Sa se enunte teorema privind rangul a doua matrice.
10) Fie A(![]() )
=
)
= 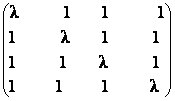 ,
,
![]()
![]() R
R
a)
Sa se gaseasca
valorile lui ![]() pentru care rang A (
pentru care rang A (![]() )
<4.
)
<4.
b)
Pentru fiecare din valorile lui ![]() gasite
mai sus sa se afle rangul lui A(
gasite
mai sus sa se afle rangul lui A(![]() ).
).
11) Sa se determine rangul matricei 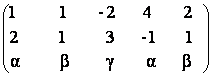 ,
,
![]() ,
,![]() ,
,![]()
![]() R
R
12) Fie matricea A =  ,
m
,
m![]() R. Ce rang maxim poate avea matricea A?
R. Ce rang maxim poate avea matricea A?
13) Fie matricele A =  B =
B = ![]() .
.
a) Se cer ![]() ,
,![]()
![]() R astfel incat rang A = 2.
R astfel incat rang A = 2.
b)
Cu ![]() si
si ![]() determinati
mai sus si sa se calculeze A
determinati
mai sus si sa se calculeze A![]() B.
B.
14) Sa se calculeze rangurile matricelor
a) 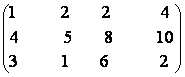 b)
b)
 c)
c)

![]()
![]() R
R
15) Sa se calculeze rangul
matricei A =  unde m
unde m![]() ,
iar a1,...., am numere diferite intre ele .
,
iar a1,...., am numere diferite intre ele .
16) Sa se afle valorile posibile ale rangului matricei
 unde a in si a mj
sunt numere oarecare.
unde a in si a mj
sunt numere oarecare.
17) Sa se afle valorile lui ![]()
![]() C pentru care matricea
C pentru care matricea
a)  are rangul minim.
are rangul minim.
18) Sa se afle rangul matricei 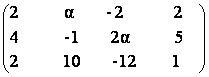 pentru
diferite valori ale lui
pentru
diferite valori ale lui ![]()
![]() C
C
19) Sa se demonstreze ca rangul unei matrice nu se schimba daca:
a) se transpune matricea;
b) se inmultesc elementele unei linii sau unei coloane cu un numar nenul;
c) se permuta intre ele doua linii (coloane);
d) se adauga la elementele unei linii (coloane) elementele corespunzatoare ale altei linii (coloane) inmultite cu un numar oarecare.
20) Sa se calculeze rangul fiecareia din urmatoarele matrici:
a)
A = b)
A=
b)
A=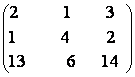
b)
A = 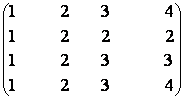 d) A =
d) A = 
e)
A =  f)
f) 
g) A =  h)
A =
h)
A = 
21) Sa se calculeze in functie de a![]() R rangul matricilor
R rangul matricilor
a) A = 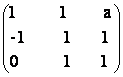 b) A =
b) A = 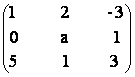
c) A =  d)
A =
d)
A = 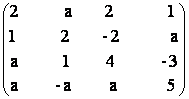
e) A = 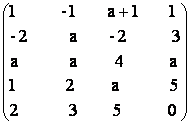 f)
A =
f)
A =
22) Sa se
calculeze in functie de a,b![]() R rangul matricilor:
R rangul matricilor:
a)A= b)A=
b)A= 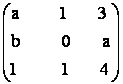 c) A =
c) A = 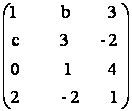
d) A=  d) A=
d) A= 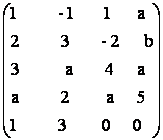
f) A = 
23) Se considera matricile:
A =  B =
B =  .
Sa se afle numerele p, q
.
Sa se afle numerele p, q ![]() R astfel incat cele doua matrice sa aiba acelasi
rang.
R astfel incat cele doua matrice sa aiba acelasi
rang.
24) Sa se
determine rangul matricei A = 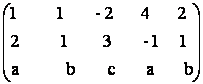
25) Sa se calculeze rangul matricilor pentru diferite valori ale parametrilor:
a)  b)
b) 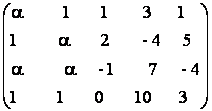
d) 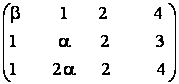 d)
d) 
26) a) Cum se poate schimba rangul unei matrici, daca se schimba unul din elementele sale?
b) Cum se poate schimba rangul unei matrici, prin schimbarea elementelor unei linii? Dar prin schimbarea elementelor a K linii?
Matrici inversabile
Sa se afle daca matricile sunt inversabile si in caz afirmativ sa se gaseasca inversele lor:
a)  b)
b)  c)
c) 
a![]() R
R
a)  b)
b) 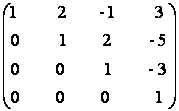
a)  b)
b) 
c) 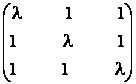 l
l
![]() C
C
4) Fie matricile A =  si B =
si B = 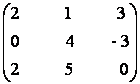 .
Sa se calculeze: 2A-2B; AB; B-1; B+ B-1.
.
Sa se calculeze: 2A-2B; AB; B-1; B+ B-1.
5) Sa se gaseasca matricile adjuncte ale urmatoarelor matrici:
A = 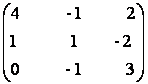 B =
B = 
6) Sa se verifice daca urmatoarele matrici sunt inversabile si in caz afirmativ sa se calculeze inversele lor:
A =  B =
B =  C =
C = 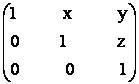
7) Fie matricile A=  B=
B= 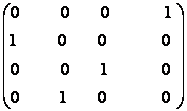 Se cere:
Se cere:
a) Sa se arate ca AB = BA = I;
b) Sa se calculeze A-1si B-1 si sa se justifice rezultatul punctului a).
8) Sa se stabileasca daca urmatoarele matrici sunt inversabile si sa se gaseasca inversele lor:
A =  B =
B = 
9) Sa se determine valorile parametrului real m, astfel incat matricea
A =  sa fie inversabila pentru orice x
sa fie inversabila pentru orice x![]() R.
R.
10) Fie matricea A = 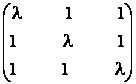
![]() M3 (C). Sa se
afle valorile lui l pentru care matricea A este inversabila si sa se
calculeze in acest caz A-1.
M3 (C). Sa se
afle valorile lui l pentru care matricea A este inversabila si sa se
calculeze in acest caz A-1.
11) Fie matricea A = 
![]() M3 (R), unde a
M3 (R), unde a![]() R
R
a) Sa se determine a, astfel incat A sa fie inversabila;
b)
Sa se determine a, astfel
incat sa existe B ![]() M3 (R), B
M3 (R), B![]() 0 cu A.B = 0.
0 cu A.B = 0.
12) Sa se rezolve ecuatiile matriceale:
a)
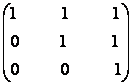 .X .
.X .  =
=  ;
;
b)
 .X
=
.X
= 
13) Sa se rezolve ecuatia matriceala
X
.  =
= 
14)
Daca X ![]() M3 (R) sa se rezolve
ecuatia matriceala:
M3 (R) sa se rezolve
ecuatia matriceala:
X .  =
= 
15) Sa se rezolve pe cale matriceala:

16) Sa se determine a![]() R, astfel incat urmatoarele matrici sa fie inversabile si
sa se afle inversele lor:
R, astfel incat urmatoarele matrici sa fie inversabile si
sa se afle inversele lor:
a) A =  b) A =
b) A = 
c) A =  d) A =
d) A = 
e) A =  f) A =
f) A = 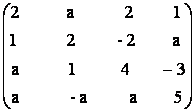
17) Sa se rezolve ecuatiile matriceale:
a) X .  =
= 
b) X . 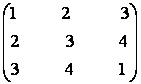 =
= 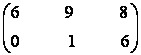
c) 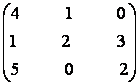
 =
= 
d)  .X =
.X = 
18) Fie A = 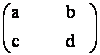
![]() M2 (C), astfel incat
A3 =0. Sa se demonstreze ca matricea
M2 (C), astfel incat
A3 =0. Sa se demonstreze ca matricea 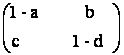 este inversabila.
este inversabila.
19) Sa se afle daca matricile urmatoare sunt inversabile si in caz afirmativ sa se gaseasca inversele lor:
a) 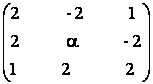 a
a![]() R .b)
R .b) 
c)  d)
d) 
20) Sa se afle daca matricile urmatoare, de ordin n, sunt inversabile si in caz afirmativ sa se gaseasca inversele lor:
a)  b)
b) 
c)  d)
d) 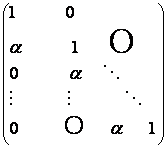
21) Sa se arate ca pentru o matrice nesingulara A de forma:
A =  inversa sa B = A-1
este de forma
inversa sa B = A-1
este de forma

22) Fie A o matrice
patratica cu coeficienti complecsi. Sa se demonstreze
ca, daca exista k ![]() 2
astfel incat Ak=0, atunci matricea I-A este inversabilasi
abem: (I-A)-1 = I+A+.+Ak-1.
2
astfel incat Ak=0, atunci matricea I-A este inversabilasi
abem: (I-A)-1 = I+A+.+Ak-1.
23) Fie A o matrice inversabila cu coeficienti complecsi. Sa se demonstreze ca (A-1)t = (At)-1.
24) Fie A, B, C matrice astfel incat AB = AC. Sunt oare egale matricele B si C? Dar daca A este o matrice nesingulara?
25) Fie E matricea patratica de ordin n ale carei elemente sunt egale cu 1. Sa se arate ca:
a) En2 = nEn
26) Fie A ![]() Mn (C) de rang 1. Sa se arate ca:
Mn (C) de rang 1. Sa se arate ca:
a) exista un numar astfel incat A2 = aA;
b) daca a ![]() -1 atunci matricea I+A este
inversabila si avem:
-1 atunci matricea I+A este
inversabila si avem:
(I+A) -1 = I - ![]()
Sa se deduca: 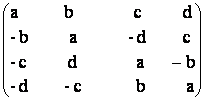 inversabila daca si numai
daca este nenula si sa se calculeze inversa.
inversabila daca si numai
daca este nenula si sa se calculeze inversa.
27) Fie A o matrice nesingulara si B = XY, o matrice de rang
1. Sa se demonstreze ca daca matricea A+B este nesingulara,
inversa sa este data de: (A+B)-1 = A-1![]() B
A -1, unde a = Y A -1X.
Presupunand cunoscute matricele A-1, X, Y, sa se calculeze
numarul inmultirilor si impartirilor necesare pentru a
trece de la A-1 la (A+B)-1.
B
A -1, unde a = Y A -1X.
Presupunand cunoscute matricele A-1, X, Y, sa se calculeze
numarul inmultirilor si impartirilor necesare pentru a
trece de la A-1 la (A+B)-1.
DETERMINANTI
Sa se calculeze:
a) ![]() ;
b)
;
b) 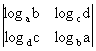 .
.
Fie ![]() =
=
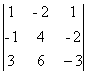 Sa se calculeze
Sa se calculeze ![]() utilizand:
utilizand:
a) Regula lui Sarrus;
b) Regula triunghiului;
c) dezvoltarea dupa linia a 3-a;
d) dezvoltarea dupa coloana a 2-a;
e) dezvoltarea dupa linia 1-a, dupa ce in prealabil se vor obtine 2 elemente zero;
f) proprietatile determinantilor.
3) Sa se calculeze determinantii:
a)  ; b)
; b)  ; c)
; c)  ; d)
; d) 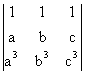 .
.
4) Sa se calculeze urmatorii determinanti:
a) 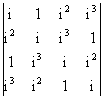 ;
b)
;
b) 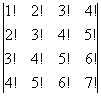 .
.
5) a) 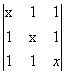 ; b)
; b) 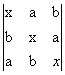 ;
c)
;
c) 
6) 
7) Sa se calculeze urmatorul determinant, punand sub formp de produs rezultatul:
![]() =
=

] 8) Fie ha, hb, hc, lungimile inaltimilor corespunzatoare laturilor de lungime a,b,c ale unui triunghi oarecare ABC. Sa se arate ca:
![]() =
= 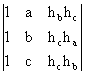
9) Fie determinantul ![]() =
= 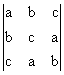
a)
Sa se calculeze ![]() punand
rezultatul sub forma de produs de 3 factori;
punand
rezultatul sub forma de produs de 3 factori;
b)
Dezvoltand pe ![]() prin doua metode diferite sa se
gaseasca egalitatea
prin doua metode diferite sa se
gaseasca egalitatea
a3+ b3 c3- 3abc = (a+b+c)( a2 + b2
+ c2 +ab-ac-bc).
10)
Dandu-se ![]() 1
=
1
= 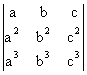 ;
; ![]() 2
2  .
.
11) Sa se dezvolte determinantii trigonometrici:
a)  ; b)
; b) 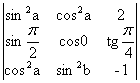 ;
c)
;
c) 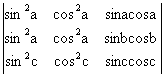
d) 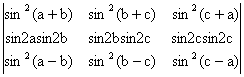 .
.
12) Daca A,B,C sunt unghiurile unui triunghi oarecare ABC sa se arate ca urmatorii determinanti au valoarea zero:
a) 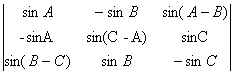 b)
b)  ;
;
c)  .
.
13) Sa se rezolve urmatorii determinanti:
a)  ;
b)
;
b)  ;
c)
;
c)  ;
d)
;
d) ![]() .
.
14) Sa se rezolve ecuatiile:
a) 0 = 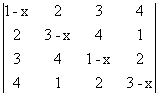 ;
b) 0 =
;
b) 0 = 
15) Fie numerele Ni = ![]() scrise in baza 10, i =
1,2,3. Daca cele trei numere sunt divizibile cu 31, atunci si
determinantul
scrise in baza 10, i =
1,2,3. Daca cele trei numere sunt divizibile cu 31, atunci si
determinantul ![]() =
=  este divizibil cu 31. Sa se generalizeze pentru n numere a
cate n cifre si pentru un divizor oarecare b
este divizibil cu 31. Sa se generalizeze pentru n numere a
cate n cifre si pentru un divizor oarecare b ![]() Z
Z ![]() .
.
16)
Sa se determine a, astfel incat ecuatia  = 0 sa admita o
radacina dubla numar intreg.
= 0 sa admita o
radacina dubla numar intreg.
17) Sa se calculeze determinantii:
a)  =
= 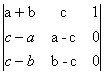 =0;
=0;
b) 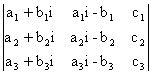 = -i
= -i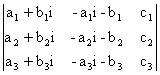 =0
=0
18) Stiind ca
radacinile x1, x2, x3 ale
ecuatiei X3 + X2 +ax+b =0; a,b ![]() R sunt reale, sa se arate
ca acestea sunt egale daca si numai daca
R sunt reale, sa se arate
ca acestea sunt egale daca si numai daca 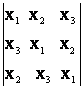 = 0.
Sa se rezolve in acest caz ecuatia data si sa se
determine a si b.
= 0.
Sa se rezolve in acest caz ecuatia data si sa se
determine a si b.
19)
Sa se calculeze determinantul ![]() =
= 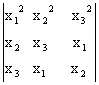 ,
stiind ca x1, x2, x3 sunt radacinile
ecuatiei: X3 - X2 +5x-2 =0.
,
stiind ca x1, x2, x3 sunt radacinile
ecuatiei: X3 - X2 +5x-2 =0.
20) Cu ce semn va aparea in determinantul de ordinul 5 termenii:
a) a14 a23 a31 a45 a52;
b) a12 a25 a33 a41 a54.
21) In determinantul de ordin 4 se gasesc termenii urmatori?
a) a13 a24 a33 a42;
b)a14 a23 a33 a41.
22) Cu ce semn apare in determinantul de ordinul n, produsul elementelor de pe diagonala principala?
23) Dar de pe diagonala secundara
sgn ![]() =
(-1)
=
(-1)![]() .
.
24) Sa se scrie toti termenii care apar in determinantul de ordin 6 si sunt de forma a15 a24 a3k3 a41 a5k5 a62.
25) Folosind numai definitia determinantilor de ordin n sa se calculeze
a) 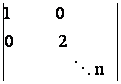 =
n!; b)
=
n!; b) 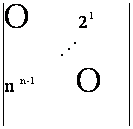 =
(-1)
=
(-1)![]() n!
n!
26) Fie d = (aij)![]() unde
aij sunt numere complexe. Daca aij=
unde
aij sunt numere complexe. Daca aij= ![]() oricare i,j atunci d este real.
oricare i,j atunci d este real.
27) Sa se verifice egalitatile:
a) 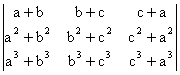 = 2abc(a-b)(b-c)(c-a)
= 2abc(a-b)(b-c)(c-a)
b) 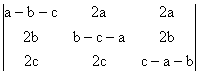 = (a+b+c)3;
= (a+b+c)3;
c)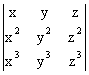 = (xy+yz+zx)(x-y)(z-x);
= (xy+yz+zx)(x-y)(z-x);
d) 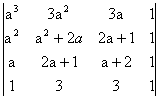 = (a-1)6.
= (a-1)6.
28)
Sa se rezolve ecuatia: 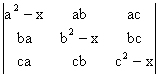
29) Sa se rezolve ecuatia:  = 0
= 0
30)
Sa se rezolve ecuatia:  = 0
= 0
31)
Sa se calculeze determinantul de ordin n: 
32) Sa se calculeze
determinantul 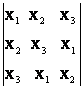 stiind
ca x1, x2, x3 sunt
radacini ale ecuatiei X3 -2X2 +2x+17= 0.
stiind
ca x1, x2, x3 sunt
radacini ale ecuatiei X3 -2X2 +2x+17= 0.
33) Sa se calculeze
determinantul d =  stiind
ca x1, x2, x3, x4 sunt radacini ale ecuatiei X4
+pX2 +qx + r= 0.
stiind
ca x1, x2, x3, x4 sunt radacini ale ecuatiei X4
+pX2 +qx + r= 0.
34) Sa se demonstreze
prin inductie dupa n: 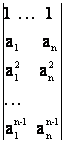 =
= ![]()
35) Sa se calculeze urmatorii determinanti:
a)  ; b)
; b)  ;
c)
;
c) 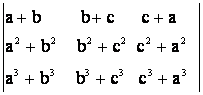 ;
;
c)
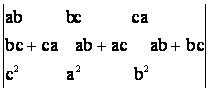 ; e)
; e) 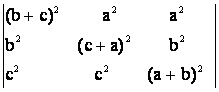 ;
;
f) 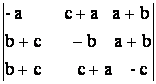 .
.
36) Sa se rezolve ecuatiile urmatoare:
a) 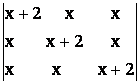 =0; b)
=0; b)  = 0; c)
= 0; c) 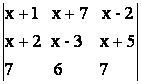 = 0;
= 0;
d) 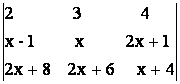 = 0; e)
= 0; e) 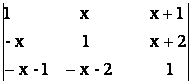 = 0;
= 0;
f) 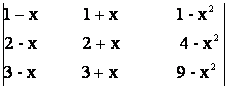 = 0; g)
= 0; g) 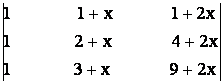 = 0; h)
= 0; h) 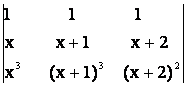 = 0; i)
= 0; i) 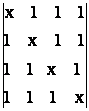 = 0;
= 0; 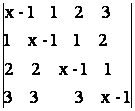 = 0.
= 0.
37) Fara a dezvolta sa se demonstreze urmatoarele egalitati:
a)
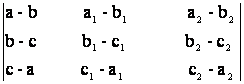
b) 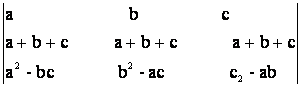
c)  = 0; d)
= 0; d)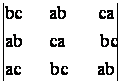 = 0; e)
= 0; e)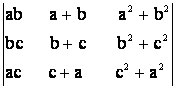 = 0; f)
= 0; f) 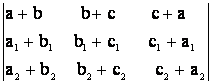 = 0; g)
= 0; g)  = 0
= 0
h)  = 0; i)
= 0; i) 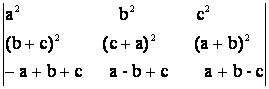 = 0
= 0
38) Sa se calculeze urmatorii determinanti:
a) 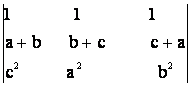 b)
b) 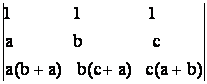 ;
;
c)  ;
d)
;
d)  .
.
39) Sa se demonstreze urmatoarele inegalitati:
a)  0,
a, b
0,
a, b ![]() R
R
b)  0;
0;
c)  0,
a, b, c
0,
a, b, c![]() R
R
d) 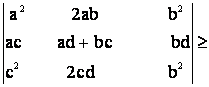 0;
e)
0;
e)  0;
0;
f)  0;
g)
0;
g) 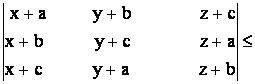 0
a,b,c,x,y,z
0
a,b,c,x,y,z![]() R
R
40) Sa se calculeze
determinantul  , stiind ca numerele a1,.
sunt:
, stiind ca numerele a1,.
sunt:
a) in progresie aritmetica;
b) in progresie geometrica.
41)
Sa se determine a![]() R astfel
incat ecuatia
R astfel
incat ecuatia 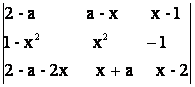 = 0 sa aiba o
radacina dubla numar intreg.
= 0 sa aiba o
radacina dubla numar intreg.
42)
Sa se calculeze determinantul ![]() =
= 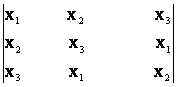 ,
stiind ca x1, x2, x3 sunt
radacinile ecuatiei X3 +pX +q = 0.
,
stiind ca x1, x2, x3 sunt
radacinile ecuatiei X3 +pX +q = 0.
43) Sa se calculeze urmatorii determinanti de ordin n:
a) 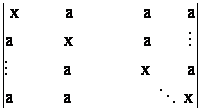
b)  ;
c)
;
c)  ;
;
d) 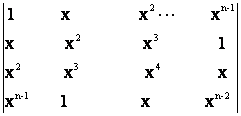 ;
e)
;
e)  ;
f)
;
f)  .
.
44)
Sa se rezolve ecuatia: c = 0, a![]() R
R
45) Sa se arate ca
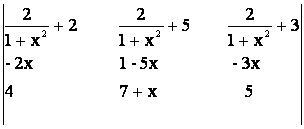 = 0.
= 0.
46) Se
considera f(x) = ![]() ,
g(x) =
,
g(x) = ![]() ,
h(x) =
,
h(x) = ![]() .Sa se arate ca
oricare ar fi tripletul a,b,c
.Sa se arate ca
oricare ar fi tripletul a,b,c ![]()
![]() avem:
avem:  = 0.
= 0.
47) Sa se arate ca:
![]() =
=  = 1+ x1 + . + xn
= 1+ x1 + . + xn
48)
Daca numerele ![]() ,
, ![]() ,
.
,
. ![]() sunt divizibile cu N atunci determinantul
sunt divizibile cu N atunci determinantul 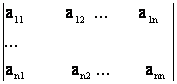 este
divizibil cu N.
este
divizibil cu N.
49)
Sa se rezolve ecuatia:  = 0.
= 0.
50)
Daca p < m atunci  = 1.
= 1.
51) Fie
ecuatia algebrica Xn +a2 Xn-2 + a3 Xn-3
+ . + an = 0, a2 , ., an![]() C. Sa se calculeze determinantul
C. Sa se calculeze determinantul
 .
.
52)
Sa se calculeze determinantul de ordinul n 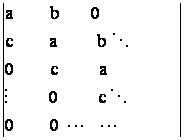 .
.
53)
Sa se arate ca:  = (y2-y1) ..(yn-y1).
= (y2-y1) ..(yn-y1).
54)
Sa se arate ca  = 0, unde a, b, c sunt lungimile corespunzatoare
laturilor unui triunghi, iar ha, hb, hc sunt
lungimile inaltimilor corespunzatoare.
= 0, unde a, b, c sunt lungimile corespunzatoare
laturilor unui triunghi, iar ha, hb, hc sunt
lungimile inaltimilor corespunzatoare.
55) Fie
matricea de ordinul 2: A = 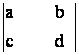 .
.
i) Sa se arate egalitatea: A2 - (a+d)A + (ad-bc)I = 0;
ii)
daca exista un k![]() 2
astfel incat Ak = 0 atunci A2 = 0.
2
astfel incat Ak = 0 atunci A2 = 0.
56) Fie
A = ![]() ,
aij
,
aij ![]() R,
B =
R,
B = 
![]() Mn (R).
Sa se arate ca, pentru n = 2,3: det.(A+B)
Mn (R).
Sa se arate ca, pentru n = 2,3: det.(A+B) ![]() det.(A-B)
det.(A-B) ![]() (det.A)2 .
(det.A)2 .
57) Sa se calculeze valoarea maxima (respectiv minima) a determinantilor de ordinul 4 ale caror elemente sunt -1 si +1.
58) Sa se calculeze urmatorii determinanti:
i) ![]() =
=  ; ii)
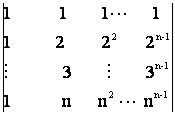
; ii) ![]() =
= 
iii) ![]() =
= 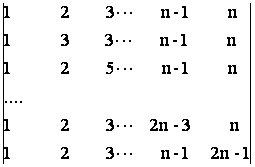
iv)![]() =
= 
v) ![]() =
= 
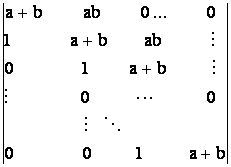
vi) ![]() =
= 
vii) ![]() =
= 
viii) ![]() =
= 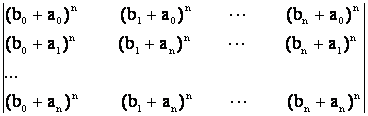
ix) ![]() =
= 
x) ![]() =
= 
59) Fie
f un polinom de gradul n cu f ![]() R
R![]() si f (k)
derivata de ordin K
si f (k)
derivata de ordin K![]()
![]() a polinomului f. Sa se demonstreze ca determinantul
urmator este independent de x.
a polinomului f. Sa se demonstreze ca determinantul
urmator este independent de x.
![]() =
= 
60) Un
determinant ![]() de ordinul 3 are elementele de pe diagonala principala egale cu
de ordinul 3 are elementele de pe diagonala principala egale cu ![]() ,
iar suma elementelor
de pe fiecare linie si de pe fiecare coloana este egala cu 1.
Sa se demonstreze ca
,
iar suma elementelor
de pe fiecare linie si de pe fiecare coloana este egala cu 1.
Sa se demonstreze ca ![]() > 0.
> 0.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6642
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved