Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
AstronomieBiofizicaBiologieBotanicaCartiChimieCopii
Educatie civicaFabule ghicitoriFizicaGramaticaJocLiteratura romanaLogica
MatematicaPoeziiPsihologie psihiatrieSociologie


IMAGINEA UNEI FUNCTII - PREIMAGINEA UNEI FUNCTII

Matematica



+ Font mai mare | - Font mai mic



IMAGINEA UNEI FUNCTII. PREIMAGINEA UNEI FUNCTII.

Fie : A B. Din definitia functiei, fiecarui element x I A I se asociaza prin functia un unic element (x) I B, numit imaginea lui x prin sau valoarea functiei in x.




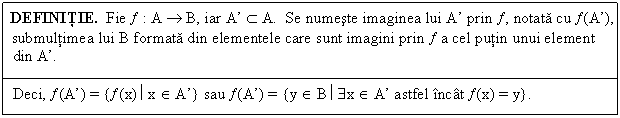
EXEMPLE. Consideram functia : data prin diagrama cu sageti.

Fie A' = .

Atunci (A') = =

A B


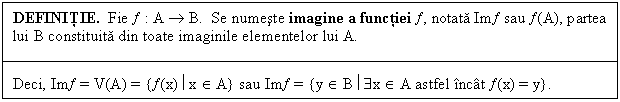
EXEMPLE. In functia : definita cu ajutorul diagramei cu sageti.

Atunci Im B.

DEFINITIE. Fie : A B.    Se numeste imaginea reciproca a unei    parti B' a lui B, notata (B'), submultimea lui A formata din acele elemente ale caror imagini prin apartin lui B'.

Deci, (B') = .
 



A B

EXEMPLE. Se considera functia : definita prin diagrama cu    sageti.

In acest caz, () = , deoarece

() = pentru ca

() = , deoarece

A B


Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 9583
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved