| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
MARIMILE MEDII
Notiuni teoretice privind marimile medii
Media aritmetica
Modul
Mediana. Quantilele
Mediala
Marimi medii cu aplicatie speciala
Relatii intre valorile marimilor medii
Notiuni teoretice privind marimile medii
In centrul metodelor si tehnicilor elaborate de statistica pentru reprezentarea sintetica a colectivitatilor se situeaza marimile medii.
In prima jumatate a secolului al XIX- lea, media devine in statistica o categorie atat de insemnata, incat unii statisticieni legau de ea insusi obiectul statisticii. Statisticienii au fost preocupati de cautarea unor tehnici de calcul superioare, dar si de ideea de a justifica stiintific notiunea de medie. S-a ajuns astfel ca media sa reprezinte o categorie metodologica specializata, cea mai cuprinzatoare si specifica statisticii, cu forme de calcul variate.
Statistica a elaborat o teorie a mediei, teorie bazata pe principiul compensarii reciproce a influentei factorilor intamplatori, neesentiali.
Reglarea influentei factorilor intamplatori ce intervin in dezvoltarea fenomenelor de masa se realizeaza conform asa-numitei legi a numerelor mari. Enuntata de Jakob Bernoulli inca din sec. 18, aprofundata de matematicianul Poisson (care ii da si numele de lege a numerelor mari), aceasta lege stabileste in esenta ca in cercetarea unui fenomen de masa, cu cat se cuprinde un nr. mai mare de cazuri, cu atat erorile intamplatoare isi vor micsora mai mult influenta asupra nivelurilor reprezentative ale fenomenului.
Media este o metoda de separare a influentelor venite pe calea factorilor intamplatori in dezvoltarea colectivitatilor.
Media este o categorie metodologica a statisticii avand rolul de a caracteriza in mod sintetic nivelurile individuale ale unei caracteristici definite intr-o colectivitate statistica, scotand in evidenta ceea ce este esential, legic in continutul acelei caracteristici.
In statistica contemporana se utilizeaza un numar mare de marimi medii care difera intre ele atat prin definitia lor, prin modul de calcul, cat si prin continutul si rolul lor specific pe care il au in cercetarea statistica.
Astfel, se cunosc:media aritmetica, media cronologica, media patratica, mediile mobile, media armonic, media geometrica, mediana, modul, mediala etc.
In functie de modul de determinare, marimile medii sunt:
-marimi medii de pozitie, ce cuprind: mediana, modul si mediala si se determina prin identificarea termenului care cuprinde in serie grupa elementelor normale, reprezentative.
-marimi medii de calcul, cuprind toate celelalte medii.
In calculul acestor medii se succed 2 operatii matematice:
-acumularea tuturor nivelurilor individuale (realizata prin insumare sau produs),
-revenirea la un nivel reprezentativ pentru toti termenii inclusi in calcul (realizata prin impartire sau extragere de radical).
Dupa locul pe care-l ocupa in practica statisticii, marimile medii pot fi:
- marimi medii fundamentale, cuprind media aritmetica, mediana, modul si se utilizeaza in mod curent in statistica,
- marimi medii cu aplicatie speciala, cuprind media geometrica, patratica, armonica, mobila, progresiva, medii care se utilizeaza in cazuri speciale.
In functie de felul seriei pentru care se calculeaza, marimile medii sunt:
medii simple, se calculeaza in serii simple,
medii ponderate, se calculeaza in serii cu frecvente.
Indiferent de natura lor, marimile medii trebuie sa satisfaca mai multe conditii generale, cunoscute in literatura de specialitate sub denumirea de conditiile lui Yule, dupa numele statisticianului englez care le-a formulat pentru prima data.
Aceste conditii sunt:
-marimile medii trebuie definite in mod precis si obiectiv, indiferent de aprecierea subiectiva a fiecarui cercetator;
-marimile medii trebuie sa fie reprezentative, adica sa reprezinte toti termenii seriei;
-media trebuie sa aiba o semnificatie concreta, usor de conceput si observat chiar pentru nespecialisti;
-media trebuie sa fie simplu de calculat si sa se preteze la calcule algebrice ulterioare;
-media trebuie sa fie cat mai putin sensibila la fluctuatiile de selectie. Adica, indiferent prin ce esantioane s-ar obtine datele asupra unei colectivitati, media rezultata trebuie sa fie aproximativ aceeasi.
In general, nu toate aceste conditii pot fi satisfacute de orice marime medie.
Media aritmetica
Definitie si mod de calcul
Media aritmetica este cel mai des utilizata in practica statisticii, facand parte din categoria mediilor fundamentale si de calcul.
Notata cu ![]() , media se calculeaza atat pentru serii simple, cat
si pentru serii cu frecvente.
, media se calculeaza atat pentru serii simple, cat
si pentru serii cu frecvente.
Media aritmetica simpla se foloseste pentru seriile in care fiecare nivel al caracteristicii este purtat de o singura unitate statistica.
Calculul acestei medii presupune insumarea nivelurilor individuale ale caracteristicii si impartirea la numarul lor.
Consideram seria: x1, x2, x3,,xn. Media aritmetica se va calcula astfel:
![]() sau
sau 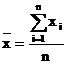 ,
, ![]() , n=volumul
colectivitatii
, n=volumul
colectivitatii
Ex. Valoarea vanzarilor realizate la nivelul unei firme in 6 zile se prezinta astfel (mil. lei): 700, 650, 850, 750, 500, 450.
Sa se calculeze valoarea medie zilnica a vanzarilor firmei.
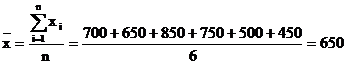 mil. lei.
mil. lei.
Media aritmetica ponderata se foloseste in cazul seriilor cu frecvente. In acest caz, se va tine seama de marimea frecventei corespunzatoare fiecarui nivel al caracteristicii.
Daca x1, x2, x3,,xm sunt niveluri individuale ale ale caracteristicii, iar n1, n2, n3,,nm nivelurile corespunzatoare frecventelor, atunci media ponderata se va calcula astfel:
![]() sau
sau 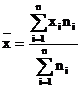
Ex. Gruparea salariatilor dupa productia orara (buc.):
|
Grupe sal. dupa productie |
Nr. sal. |
|
|
Total |
Sa se determine productia medie orara.
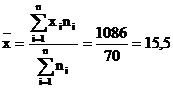 buc.
buc.
Cand intr-o serie calitativa cu atribut cantitativ, caracteristica este data sub forma de intervale, inainte de a aplica relatia de calcul a mediei, se va proceda la inlocuirea fiecarui interval prin cate o singura varianta a caracteristicii. Aceasta varianta este data de centrul intervalului, determinat ca o medie aritmetica simpla a limitelor intervalelor.
Ex. Gruparea muncitorilor dupa timpul nefolosit productiv zilnic (minute):
|
Grupe muncit. dupa timp |
Nr. muncit. ni |
xi |
|
|
Total |
Sa se determine timpul nefolosit productiv zilnic in medie de un muncitor.
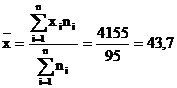 minute.
minute.
Din definitia mediei aritmetice rezulta ca aceasta este sensibila la prezenta valorilor aberante, adica daca seria are o valoare cu mult diferita ca marime fata de celelalte valori, atunci media nu mai exprima seria. In astfel de cazuri se elimina valoarea aberanta in vederea calcularii unei medii reprezentative.
Proprietati ale mediei aritmetice
Media aritmetica are o serie de proprietati:
Aceasta proprietate exprima faptul ca media aritmetica a unei variabile statistice este cuprinsa intre cea mai mica si cea mai mare valoare a caracteristicii.
![]() <
< ![]() <
< ![]()
Daca in seria x1, x2, x3,, xi,,xm
n1, n2, n3,,nm
consideram ca x1=x2= x3== xi==xm=k,
atunci:
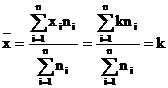
Daca se inlocuiesc, in cadrul unei serii statistice, mai multe niveluri individuale ale caracteristicii cu media lor, atunci media seriei nu se schimba. In particular, daca intr-o serie statistica se inlocuiesc toate nivelurile individuale ale caracteristicii cu media lor, atunci valoarea totala a caracteristicii ramane neschimbata.
Daca se micsoreaza fiecare nivel individual al caracteristicii dintr-o serie cu o cantitate constanta "a", media se micsoreaza cu acea constanta.
Pe baza acestei proprietati, rezulta urmatoarele formule de calcul simplificat a mediei aritmetice:
-pt.
serii simple: 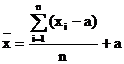
-pt.
serii ponderate: 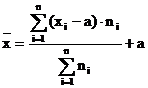
Pentru o simplificare maxima a calculelor, constanta "a" se alege egala cu un nivel al caracteristicii din centrul sirului xi.
e. Daca se micsoreaza fiecare varianta a caracteristicii de un anumit numar de ori "k", atunci media seriei se micsoreaza de acelasi numar de ori.
Se obtin urmatoarele relatii:
-pt.
serii simple: 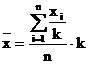
-pt.
serii ponderate: 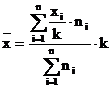
Pentru obtinerea unor simplificari maxime a calculelor, valoarea constantei "k" se alege egala cu cel mai mare divizor comun al variabilelor xi.
f. Daca frecventele seriei se micsoreaza de un numar "c" de ori, atunci media aritmetica ramane neschimbata.
Aceasta proprietate se aplica numai seriilor cu frecvente.
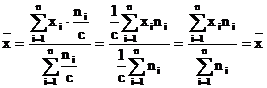
Valoarea constantei "c" se considera agela cu cel mai mare divizor comun al frecventelor, pentru a obtine o simplificare mai mare a calculelor.
g. Suma algebrica a abaterilor nivelurilor individuale ale caracteristicii de la media lor este egala cu zero.
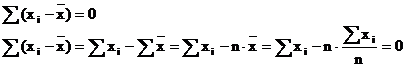
Aceasta proprietate ne arata ca media caracteristicii este o valoare reprezentativa a seriei.
Utilizand concomitent proprietatile enuntate se obtin urmatoarele formule de calcul simplificat al mediei aritmetice:
-pt.
serii simple: 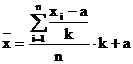
-pt.
serii ponderate: 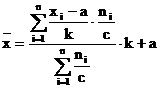
Ex. Gruparea muncitorilor dupa nr. de piese realizate lunar se prezinta astfel:
|
Grupe muncit. dupa prod. |
Nr. muncit. ni |
xi |
xini |
a=290 xi-a |
k=10
|
c=5
|
|
|
|
|||||||
|
Total |
Sa se determine nr. mediu de piese realizate lunar de un muncitor cu ajutorul calculului simplificat al mediei aritmetice.
-media
aritmetica ponderata: 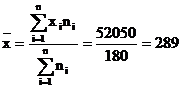 piese
piese
-calcul
simplificat: 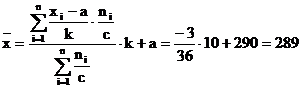 piese.
piese.
Media unei caracteristici alternative
Caracteristicile alternative sunt acele caracteristici la care, pentru fiecare unitate, apare fie forma sa de manifestare directa, fie opusul ei.
Unitatile colectivitatii se pot imparti in doua parti:
-unele la care se inregistreaza forma directa de manifestare a unei caracteristici;
-altele la care se inregistreaza opusul ei.
Pentru a le exprima numeric se vor considera in mod conventional variantele cu raspuns afirmativ ca avand valoarea 1, iar variantele cu raspuns negativ ca avand valoarea zero.
Daca notam cu "n" numarul total al unitatilor colectivitatii si cu "n1" efectivul acelor unitati care au valoarea 1, atunci efectivul celor care nu poarta acea caracteristica va fi (n-n1).
Media, in cazul caracteristicii alternative, este egala cu ponderea unitatilor care poarta caracteristica in totalul unitatilor colectivitatii. Aceasta se noteaza cu "p" si se calculeaza astfel:
![]()
Media unitatilor care nu poarta acea caracteristica se noteaza cu "q" si se determina astfel:
![]()
Intre p si q se verifica relatia:
p+q=1.
Ex. Dintr-un lot de 500 de piese supuse controlului de calitate s-au gasit 60 de piese rebut. Sa se determine media rebuturilor din lot si media unitatilor care nu poarta caracteristica de rebut.
n=500
n1=60
![]()
La fiecare 100 piese receptionate pot sa apara cate 12 rebuturi.
![]()
p+q=0,12+0,88=1.
Modul
Denumit si dominanta, modul face parte din marimile fundamentale de pozitie.
Modul este valoarea caracteristicii cel mai des observata intr-o distributie, respectiv valoarea ce corespunde frecventei dominante. Ca urmare, modul se determina numai in cazul seriilor cu frecvente.
In cazul seriilor in care caracteristica se prezinta sub forma de variante, pentru aflarea modului parcurgem etapele:
-se gaseste frecventa maxima a seriei;
-se identifica modul ca fiind valoarea caracteristicii corespunzatoare frecventei maxime.
Daca seria este plurimodala, atunci modul este dat de valoarea caracteristicii care se intalneste cel mai frecvent.
Ex. Gruparea muncitorilor dupa productia lunara (metri) se prezinta astfel:
|
Grupe muncit. dupa prod. xi |
Nr. muncit. ni |
Sa se determine productia medie lunara pe un muncitor cu ajutorul modului.
-frecventa maxima = 60
-modul = 170.
Pentru seriile in care caracteristica se prezinta sub forma de intervale de variatie, determinarea modului se poate realiza prin calcul si pe cale grafica.
Prin calcul se parcurg operatiile:
-aflarea frecventei maxime;
-identificarea intervalului modal, ca interval al caracteristicii corespunzator frecventei maxime;
-aplicarea relatiei de calcul a modului:
![]() , unde:
, unde:
x0 = limita inferioara a intervalului modal,
d = marimea intervalului modal,
![]() = diferenta
dintre frecventa intervalului modal si frecventa intervalului
anterior celui modal,
= diferenta
dintre frecventa intervalului modal si frecventa intervalului
anterior celui modal,
![]() = diferenta
dintre frecventa intervalului modal si frecventa intervalului
urmator celui modal.
= diferenta
dintre frecventa intervalului modal si frecventa intervalului
urmator celui modal.
Pe cale grafica, modul se determina pe baza histogramei. Se reprezinta grafic seria cu ajutorul hististogramei, urmand apoi determinarea punctului densitatii maxime a frecventelor, in cadrul intervalului modal. Pentru aceasta, in coloana cea mai inalta, corespunzatoare intervalului modal, se traseaza diagonalele care unesc colturile bazei de sus a acestuia cu colturile coloanelor vecine. Din punctul lor de intersectie se coboara perpendiculara pe axa absciselor si marimea obtinuta este modul.
Modul are avantajul de a fi determinat foarte rapid si are semnificatie directa, simpla. Se utilizeaza pentru a obtine o prima estimare a valorii centrale a unei distributii.
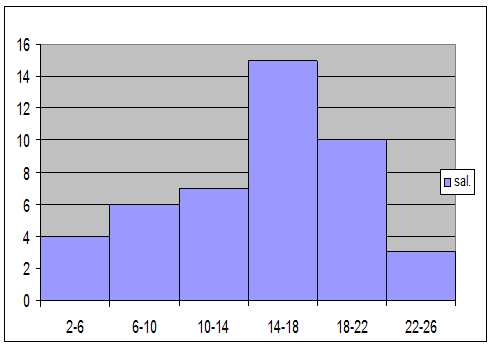
Ex. Gruparea salariatilor unui atelier dupa productia zilnica (metri) se prezinta astfel:
|
Grupe sal. dupa prod. |
Nr. sal. |
|
| |
|
Total |
Sa se determine productia medie zilnica cu ajutorul modului, prin calcul si grafic.
-frecventa maxima = 15,
-interv. Modal = (14-18),
-![]() m
m
![]()
![]()


Mediana
Mediana este valoarea centrala a unei colectivitati, ea impartind efectivul, ordonat dupa marimea caracteristicii, in doua parti egale.
Pentru a calcula mediana, se determina mai intai unitatea mediana, ca unitate care imparte in 2 parti egale efectivul unei colectivitati.
Mediana poate fi definita ca valoare a caracteristicii purtate de unitatea mediana.
Metodologia de calcul a medianei este diferita dupa natura seriei luate in calcul.
Pentru serii simple se intalnesc doua situatii:
-seria
are un numar impar de termeni, cand mediana este acea varianta a
caracteristicii cu rangul ![]() , dupa ce in prealabil seria a fost ordonata
crescator, unde n = nr. termenilor.
, dupa ce in prealabil seria a fost ordonata
crescator, unde n = nr. termenilor.
Ex. Pp. ca 9 echipe de muncitori realizeaza zilnic urmatoarea productie (nr. piese): 30, 25, 10, 27, 18, 9, 20, 11, 22. Sa se determine productia medie zilnica cu ajutorul medianei.
ordonam seria in sens crescator:
calculam rangul medianei = ![]()
Me va fi al 5-lea termen al seriei ordonate
Me = 20 piese.
-seria are un numar par de termeni, situatie in care mediana este data de semisuma termenilor centrali ai seriei ordonate.
Ex. Sa se determine productia medie saptamanala a unei firme, cu ajutorul medianei, pe baza datelor (mii tone):
30, 28, 35, 25, 40, 32
- ordonam seria in sens crescator:
- Me = ![]() mii t.
mii t.
Pentru seriile cu frecvente, mediana se poate obtine prin calcul si grafic. Si aici intalnim 2 situatii:
-cand caracteristica se prezinta sub forma de variante, pentru obtinerea medianei prin calcul, efectuam operatiile:
o determinam sirul frecventelor cumulate Ni;
o
calculam unitatea
mediana: ![]() ;
;
o cautam locul unitatii mediane in sirul frecventelor cumulate, alegand un nivel egal sau mai mare decat aceasta;
o se identifica mediana ca fiind nivelul caracteristicii corespunzator unitatii mediane.
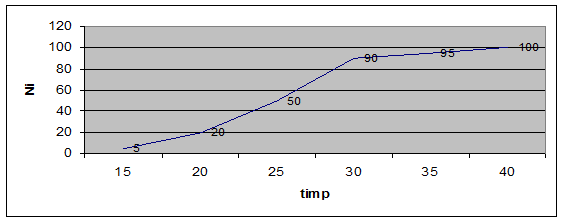
Pe cale grafica, mediana se determina cu ajutorul curbei frecventelor cumulate - ogiva. Pe axa ordonatelor se fixeaza sirul frecventelor cumulate si locul unitatii mediane. Din acest loc se duce o paralela la axa absciselor pana intalneste curba. Din acest loc se coboara perpendiculara si marimea obtinuta pe axa absciselor este Me.
Ex. Gruparea persoanelor dupa timpul de deplasare (minute):
|
Grupe pers. dupa timp xi |
Nr. pers. ni |
Ni↓ |
|
Total |
Sa se determine timpul mediu de deplasare prin intermediul medianei, prin calcul si grafic.
![]()
Me = 25 minute.
![]()
-cand caracteristica se prezinta sub forma de intervale de variatie, mediana se obtine prin calcul parcurgand urmatoarele etape:
o se determina sirul frecventelor cumulate Ni;
o
se calculeaza unitatea mediana:
![]() ;
;
o se identifica locul unitatii mediane pe sirul frecventelor cumulate, ca fiind un nivel egal sau mai mare decat aceasta;
o se afla intervalul median, ca interval corespunzator unitatii mediane
o se aplica formula de calcul a medianei:
![]() , unde:
, unde:
x0 = limita inferioara a intervalului median;
d = marimea intervalului median;
Na = frecventa cumulata anterioara intervalului median;
nMe = frecventa reala a intervalului median.
Pe cale grafica mediana se determina ca si in situatia precedenta cu ajutorul curbei frecventelor cumulate.
Ex. Gruparea salariatilor dupa productia zilnica (buc.) se prezinta astfel:
|
Grupe sal. dupa prod. |
Nr. sal. ni |
Ni↓ |
|
Total |
Sa se determine productia medie zilnica cu ajutorul medianei, prin calcul si grafic.
![]()
![]()
![]() buc.
buc.
Mediana reprezinta o marime centrala a unei serii statistice, avand un continut esential comun cu cel al mediei aritmetice. Ea nu este insa o sinteza a tuturor elementelor componente ale seriei asa cum este media aritmetica. In determinarea sa se cuprinde numai intervalul caracteristicii termenului median, celelalte fiind neglijate. Mediana poarta caracterul de marime medie aproximativa.
Quantilele
Quantilele sunt marimi medii de pozitie din sistemul medianei. Sunt valori ale caracteristicii care impart seria intr-un numar de grupe cu efective egale. Quantilele folosite in mod obisnuit sunt cele care impart colectivitatea in patru, zece sau o suta de parti egale, numite quartile, decile, centile. Quantilele se folosesc in calculul unor indicatori ai dispersiei.
Quartilele
Sunt in numar de trei si impart efectivul colectivitatii in patru parti egale. Se determina astfel:
![]()
![]()
![]()
x0 = limita inferioara a intervalului quattilic;
d = marimea intervalului quartilic;
UQ1, UQ2, UQ3 = unitatile quartilice;
Na = frecventa cumulata anterioara intervalului quartilic;
nQ1, nQ2, nQ3 = frecventele reale ale intervalului quartilic.
Pentru determinarea quartilelor se procedeaza astfel:
-se determina sirul frecventelor cumulate Ni;
-se calculeaza unitatile quartilice dupa relatiile:
![]() ;
; ![]() ;
; ![]()
-se cauta locul unitatilor quartilice pe sirul frecventelor cumulate;
-se identifica intervalele quartilice ca fiind intervalele corespunzatoare unitatilor quartilice;
-se aplica formula.
Quartilele se pot obtine si pe cale grafica cu ajutorul curbei frecventelor cumulate, asemanator medianei.
Ex. Gruparea firelor dupa rezistenta la rupere se prezinta astfel:
|
Grupe fire dupa rezistenta |
Nr. fire ni |
Ni↓ |
|
|
||
|
Total |
Sa se determine marimile medii de pozitie din sistemul medianei, prin calcul si grafic.
![]()
![]()
Intervalul quartilic 1 este (6-8).
x0 = 6; d = 2; UQ1= 27,5; Na = 21; nQ1 = 1
![]()
![]()
![]()
Intervalul quartilic 2 este (10-12).
x0 = 10; d = 2; UQ1= 55; Na = 44; nQ1 = 21.
![]()
![]()
![]()
Intervalul quartilic 1 este (12-14).
x0 = 12; d = 2; UQ1= 82,5; Na = 65; nQ1 = 35.
![]()
Decilele
Sunt in numar de 9 si impart efectivul colectivitatii in 10 parti egale. Se determina in mod asemanator medianei si quartilelor, dupa relatiile:
![]()
![]()
![]()
D5 = Me = Q2
![]()
![]()
![]()
![]()
![]()
![]() .
.
Centilele
Sunt in numar de 99 si impart efectivul colectivitatii in 100 parti egale. Se determina asemanator celorlalte marimi medii de pozitie din sistemul medianei.
Mediala
Reprezinta o alta medie de pozitie asemanatoare prin tehnica sa de calcul cu mediana.
Mediala reprezinta nivelul caracteristicii care imparte volumul total al colectivitatii in 2 parti egale.
Daca mediana imparte in 2 parti egale efectivul unei
serii (![]() ), mediala imparte in 2 parti egale volumul total
al colectivitatii (
), mediala imparte in 2 parti egale volumul total
al colectivitatii (![]() ).
).
Calculul medialei se face similar cu cel al medianei, numai ca, in
locul frecventelor cumulate, se vor considera produsele ![]() cumulate.
cumulate.
In cazul seriilor cu frecvente in care caracteristica este data pe variante, mediala se calculeaza in urmatoarele etape:
-se
determina produsele![]() ;
;
-se
calculeaza sirul produselor ![]() cumulate, notate cu Li;
cumulate, notate cu Li;
-se
determina unitatea mediala conform relatiei: ![]() ;
;
-se cauta locul unitatii mediale pe sirul Li, alegand un nivel egal sau mai mare decat acesta;
-se identifica mediala ca fiind nivelul caracteristicii corespunzator unitatii mediale.
Mediala se poate determina si e cale grafica, asemanator medianei, numai ca pe axa ordonatelor se fixeaza sirul Li si apoi se traseaza curba frecventelor cumulate.
Ex. Distributia elevilor dintr-o scoala dupa rezultatele obtinute la un test (nr. puncte):
|
Grupe elevi dupa nr. puncte xi |
Nr. elevi ni |
xini |
Li↓ |
|
Total |
Sa se determine numarul mediu de puncte obtinut de un elev, cu ajutorul medialei, prin calcul si grafic.
![]() ≥ 1406
≥ 1406
Ml = 8 puncte.
In cazul seriilor cu frecvente si caracteristica sub forma de intervale de variatie, mediala se determina tot prin calcul si grafic.
Prin calcul se parcurg operatiile:
-se
determina produsele ![]() ;
;
-se
calculeaza sirul produselor ![]() cumulate, notate cu Li;
cumulate, notate cu Li;
-se
determina unitatea mediala conform relatiei: ![]() ;
;
-se cauta locul unitatii mediale pe sirul Li, alegand un nivel egal sau mai mare decat acesta;
-se identifica intervalul medial, ca fiind intervalul caracteristicii corespunzator unitatii mediale;
-se
aplica formula medialei: ![]() , unde:
, unde:
x0 = limita inferioara a intervalului medial;
d = marimea intervalului medial;
UMl = unitatea mediala;
La = produsul cumulat anterioar intervalului medial;
![]() = produsul
= produsul ![]() corespunzator
intervalului medial.
corespunzator
intervalului medial.
Pe cale grafica, mediala se determina asemanator situatiei precedente.
Ex. Distributia dupa timpul de deplasare a unui esantion de persoane se prezinta astfel:
|
Grupe pers. dupa timp (min) |
Nr. pers. ni |
xi |
xini |
Li↓ |
|
Total |
Sa se determine timpul mediu de deplasare cu ajutorul medialei prin calcul si grafic.
xi = mijlocul intervalelor.
![]()
Interv. medial = 90-120.
x0
= 90; d = 30; UMl= 7350; La = 7125; ![]() = 4725.
= 4725.
![]()
Marimi medii cu aplicatii speciale
Media cronologica
Media armonica
Mediile mobile
Media progresiva
Media geometrica
Media patratica
Media cronologica
Este o medie care are la baza principiul de calcul al mediei aritmetice, ea fiind aplicata la determinarea nivelului mediu al seriilor cronologice de momente.
Formula mediei cronologice este o adaptare a formulei mediei aritmetice la elementele seriilor cronologice.
Termenii seriei delimiteaza perioade de timp.
Daca "n" este numarul termenilor seriei, atunci numarul perioadelor delimitate de acestia este "n-1".
In functie de distanta dintre momentele de timp ale seriei, se va calcula:
-media cronologica simpla,
- media cronologica ponderata.
Media cronologica simpla se calculeaza cand momentele sunt egal distantate intre ele.
Pentru seria ![]() ,
, 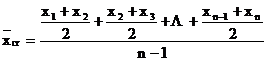 .
.
Prin transformare, aceasta
relatie devine: 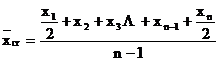 .
.
Ex. Numarul salariatilor unei firme intr-un semestru a evoluat astfel:
|
Data | ||||||
|
Nr. sal. |
Sa se determine nr. mediu lunar al salariatilor.
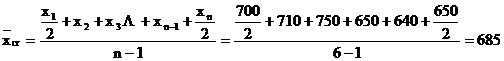 salariati.
salariati.
Media cronologica ponderata se calculeaza atunci cand intervalele de timp dintre termenii seriilor de momente sunt inegale.
In acest caz, mediile partiale, din care se calculeaza media intregii perioade, sunt ponderate cu durata perioadelor partiale dintre termenii seriei, notate cu ti.
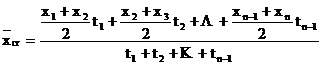
Ex. Numarul salariatilor unei firme la diferite momente de timp:
|
Data | |||||
|
Nr. sal. |
|
Sa se determine nr. mediu lunar al salariatilor.
t1 = 1 luna, t2 = 2 luni, t3 = 2 luni, t4 = 1 luna
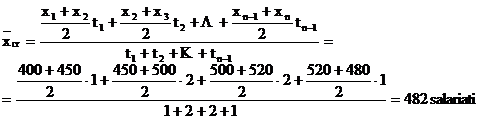
Media armonica
Este definita ca o marime inversa a mediei aritmetice, calculata din marimile inverse ale caracteristicii.
Media armonica
simpla 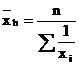
Media armonica
ponderata 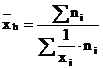
Media armonica este influentata mai mult de valorile mici ale seriei, pe cand media aritmetica este influentata de valorile mari.
In practica statisticii este utilizata, in special, in calculul indicelui mediu armonic ponderat.
Ex. Salariul mediu orar si fondul de salarii la 3 ateliere ale unei firme:
|
Atelier |
Salariu mediu xi |
Fond de salarii ni |
|
Total |
Sa se determine salariul mediu orar pe firma.
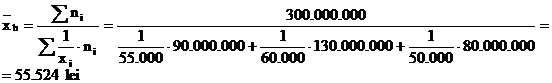
Mediile mobile
Se calculeaza ca un sir de medii aritmetice dintr-un numar determinat de termeni ai unei serii dinamice, luat prin deplasare consecutiva cu o unitate pe scara de variatie a timpului.
Mediile mobile sunt medii aritmetice pe grupuri din termenii seriei. Se pot calcula in 2 situatii:
-dintr-un nr. impar de termeni ai seriei;
-dintr-un nr. par de termeni ai seriei.
Consideram seria: ![]() .
.
-mediile mobile din cate 3 termeni:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
-mediile mobile din cate 4 termeni:
![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Mediile mobile se utilizeaza in ajustarea seriilor care caracterizeaza variatia sezoniera a fenomenelor economico-sociale. Pentru mediile mobile calculate dintr-un nr. impar de termeni se stabileste usor termenul seriei inlocuit prin media mobila. Nu acelasi lucru se intampla in cazul mediilor mobile calculate dintr-un nr. par de termeni. Pentru acestia se va proceda la centrarea mediilor mobile obtinute in prima etapa.
Centrarea consta in determinarea unor medii aritmetice din cate doua medii mobile consecutive.
Ex. Conflictele colective de munca si frecventa lor lunara au evoluat astfel:
|
Luna |
Nr. conflicte |
|
I II III IV V VI VII VIII IX X XI XII | |
|
Total |
Sa se determine numarul mediu al conflictelor de munca cu ajutorul mediilor mobile calculate din cate 5 si 6 termeni.
Medii mobile din cate 5 termeni
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Medii mobile din cate 6 termeni
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Centrarea mediilor mobile calculate din cate 6 termeni:
![]()
![]()
![]()
![]()
![]()
![]()
Media progresiva
Colectivitatile isi au progresivitatea lor, fie ca este privita in timp sau sub aspect calitativ.
Media progresiva reprezinta o medie a tipurilor de nivel calitativ superior in cadrul unei colectivitati date. In mod practic, media progresiva se gaseste intre media aritmetica generala a seriei si media termenilor calitativ superiori ai aceleiasi serii.
![]() , unde:
, unde:
![]() = media generala
a seriei;
= media generala
a seriei;
![]() = media termenilor
calitativ superiori mediei generale.
= media termenilor
calitativ superiori mediei generale.
In cazul fenomenelor in care
superioritatea se exprima cantitativ printr-o regresie, se tine seama
de acest specific al seriei. Ex.: costuri, cheltuieli, preturi, consumuri.
In acest caz, ![]() se va calcula din
termenii seriei mai mici decat media generala.
se va calcula din
termenii seriei mai mici decat media generala.
Ex. Evolutia productiei unor firme dintr-un sector de activitate (mld. lei):
|
Grupe firme dupa prod. xi |
Nr. firme ni |
|
Total |
Sa se determine productia medie a unei firme cu ajutorul mediei progresive.
![]()
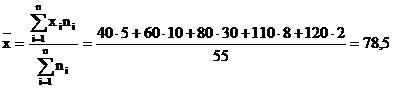 mld. lei
mld. lei
![]() mld. lei
mld. lei
![]() mld. lei
mld. lei
Ex. Gruparea firmelor dupa cheltuielile materiale (mil. lei) se prezinta astfel:
|
Grupe firme dupa chelt. |
Nr. firme ni |
xi |
xini |
|
Total |
Sa se determine nivelul mediu al cheltuielilor materiale pe o firma cu ajutorul mediei progresive.
![]()
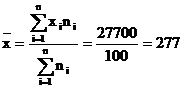 mil lei
mil lei
![]() mil lei
mil lei
![]() mil lei
mil lei
Media geometrica
Este una din cele mai importante medii cu aplicatii speciale.
Media geometrica este o medie calculata prin extragerea radacinii de un ordin egal cu numarul termenilor seriei, din produsul acestor termeni.
Media geometrica simpla
![]()
Media geometrica ponderata
![]()
In practica statisticii se utilizeaza ca metoda de calcul a ritmului de variatie in timp a fenomenelor.
Ex. Cifra de afaceri a unei firme creste cu 10% in primul an, cu 15% in urmatorii 2 ani si cu 18% in ultimul an al unei perioade de 4 ani observate.
Sa se determine cresterea medie anuala cu ajutorul mediei geometrice.
Media geometrica simpla
![]()
Cresterea medie anuala a cifrei de afaceri este de 1,145 ori sau cu 14,5%.
Media patratica
Este o marime medie calculata prin extragerea radacinii patrate din media aritmetica a patratelor termenilor seriei.
Media patratica
simpla 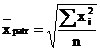
Media patratica
ponderata 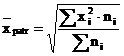
Aplicatiile acestei medii sunt legate de determinarea abaterii medii patratice, o categorie metodologica a statisticii din sistemul dispersiei.
Ex. Gruparea persoanelor dupa veniturile saptamanale (mii lei):
|
Grupe pers. dupa venit |
Nr. pers. ni |
xi |
|
xini |
|
Total |
Sa se determine veniturile medii saptamanale cu ajutorul mediei patratice.
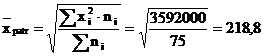 mii lei.
mii lei.
Relatii intre valorile marimilor medii
Intr-o serie "ideala", caracterizata de o simetrie perfecta a distributiei unitatilor in colectivitate, mediile fundamentale - media aritmetica, mediana, modul si mediala - coincid.
In cazul unei curbe moderat asimetrice, mediana se situeaza de obicei intre media aritmetica si dominanta, la 1 3 din distanta dintre medie si dominanta, masurata de la medie. Aceasta se poate exprima prin relatia:
![]()
Alegerea celei mai potrivite si semnificative valori centrale cere, pe de o parte un examen atent al distributiei, iar pe de alta parte cere sa se tina seama de principalele particularitati ale valorilor centrale.
Media aritmetica, fiind o medie de calcul, este influentata de fiecare valoare a seriei, ca urmare este foarte sensibila la valorile extreme. Media aritmetica poate fi utilizata in calcule algebrice ulterioare.
Modul si mediana, fiind marimi medii de pozitie, sunt influentate mai mult de numarul decat de marimea valorilor unor serii, prin urmare, nu sunt influentate de valorile aberante.
Mediana, tinand seama doar de valorile ce ocupa o pozitie centrala, se poate calcula chiar si cand nu se cunosc limitele seriei.
Modul, fiind valoarea cea mai des intalnita, cea mai frecventa intr-o serie, este valoarea cea mai tipica sau cea mai probabila, dar netinand seama de toate valorile seriei ca si mediana, se gaseste sub semnul aproximarii.
De asemenea, mediana si modul, mai au dezavantajul de a nu fi utilizate in calcule algebrice, dezavantaj compensat insa de faptul ca sunt marimi foarte usor de obtinut.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 8727
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved