| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
METODE DE REZOLVARE A PROBLEMELOR
DE CONCURENTA SI COLINIARITATE
In geometrie, ca si in celelalte ramuri ale matematicii, nu exista "chei universale", motiv pentru care prin "metode de rezolvare a problemelor" nu se intelege prezentarea unor retetare absolute, care sa asigure solutionarea problemelor pe baza unor formule cunoscute sau algoritmi prestabiliti.
Insusirea notiunilor de baza ale geometriei elementare si folosirea acestora in mod selectiv in rezolvarea problemelor constituie esenta procesului invatarii dirijate si constiente a acestei discipline.
Este esential ca rezolvitorul, dezvoltand operatiile mentale fundamentale - analiza, sinteza, comparatia, abstractizarea si generalizarea - sa imbine diferitele ipoteze si prin rationamente logice sa descopere solutia; realizandu-se in acest sens o unitate dialectica intre formativ si informativ.
In geometrie o problema rezolvata nu este un punct terminus - in timp ce serveste scopului propus in mod conttient, ea devine si o sursa de plecare pentru noi implicatii, sugestii, probleme adiacente.
In rezolvarea problemelor de geometrie este
absolut obligatorie stapanirea metodelor generale si a metodelor
particulare de rezolvare a problemelor.![]()
A. Metode generale
metoda sintezei, metoda analizei, metoda reducerii la absurd.
A1 Metoda sintezei - se dovedeste a fi utila atat in rezolvarea problemelor de calcul cat si in rezolvarea unor probleme de demonstratie. Pentru demonstrarea unor teoreme sau pentru rezolvarea unor probleme se considera o figura despre care se stie ca poseda proprietatea p si se cere sa aratam ca poseda proprietatea q, p q
Metoda sintezei consta in a pleca de la propozitia p si a descoperi alte propozitii r1, r2, , rk astfel incat p r1 r2 rk q.
Problema: Fie un triunghi ABC si punctele coliniare A , B , C unde A I (BC), B I (CA) si C I (AB).
Atunci are loc egalitatea : ![]()
![]()
![]() Teorema lui Menelaus:
Teorema lui Menelaus:
Demonstratie:
Fiind vorba de rapoarte si legaturile ce trebuiesc stabilite intre ele, apare necesitatea de a utiliza asemanarea triunghiurilor. Ne fiind triunghiuri asemenea, trebuie sa le construim.
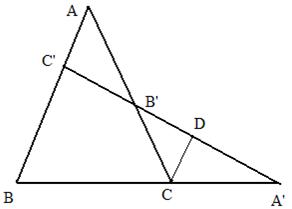
In acest sens ducem CD AB, unde DI C A
Din asemanarea triunghiurilor, obtinem:
Din D A BC D A CD T ![]()
iar
din D B CD D B AC T ![]()
Inmultind cele doua relatii, obtinem ca:
![]()
![]() de unde:
de unde: ![]()
Considerand propozitiile:
p: "punctele A', B', C' coliniare"
q: "![]() "
"
r1: "D A BC D A CD si D B CD D B AC
r2: " ![]() si
si ![]() " unde r1 si r2 sunt
conjunctii de propozitii, observam ca demnstrarea teoremei
lui Menelaus s-a bazat pe schema:
" unde r1 si r2 sunt
conjunctii de propozitii, observam ca demnstrarea teoremei
lui Menelaus s-a bazat pe schema:
p r1 r2 q
A2 Metoda analizei - este o metoda eficace in abordarea problemelor de calcul sau de demonstratie. Se demonstraza implicatia "p q"
 Se cauta o
propozitie rn care s-o implice pe q, dupa care trebuie
gasita o propozitie rn-1 din care sa deducem rn
si asa mai departe pana reusim sa gasim o
propozitie r1 care sa rezulte direct din propozitia
p.
Se cauta o
propozitie rn care s-o implice pe q, dupa care trebuie
gasita o propozitie rn-1 din care sa deducem rn
si asa mai departe pana reusim sa gasim o
propozitie r1 care sa rezulte direct din propozitia
p.
Problema:
Sa se arate ca intr-un tetraedru oarecare cele trei
![]()
![]() bimediane sunt concurente
bimediane sunt concurente
![]() Intr-un
tetraedru numim bimediana segmentul
Intr-un
tetraedru numim bimediana segmentul
care uneste mijloacele a doua muchii opuse.
Orice tetradru are sase muchii, deci exista trei
bimediane .
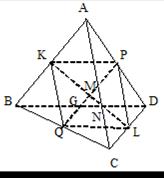
In tetraedrul ABCD consideram bimedianele [KL], [QP], [MN].
Trebuie sa dovedim implicatia "p q" unde:
p: " ABCD tetraedru, [KA] = [KB], [LC] = [LD], [MA] = [MC], [NB] = [ND], [PA] = [PD] si [QB] = [QC]"
q: " [KL], [MN], [PQ] concurente"
Se observa ca propozitiile:
t1 : "In paralelogramul KQLP diagonalele [kl], [pq] sunt concurente si se injumatatesc"
t2 : "In paralelogramul KNLM diagonalele [kl], [MN] sunt concurente si se injumatatesc"
t3 : "In paralelogramul NPMQ diagonalele [mn], [pq] sunt concurente si se injumatatesc"
implica concluzia q.
Se observa ca din propozitiile:
a1: "KQ║LP si KQ = LP"
a2: "KN║LM si KN = LM"
a3: "MP║NQ si MP = NQ" se deduc propozitiile t1, t2, t3.
Cat priveste propozitiile a1, a2, a3, acestea sunt consecinte directe ale propozitiilor:
r1: "[kq] linie mijlocie in triunghiul BAC si [LP] linie mijlocie in triunghiul DAC"
r2: "[kN] linie mijlocie in triunghiul BAD si [LM] linie mijlocie in triunghiul CAD"
r3: "[MP] linie mijlocie in triunghiul ACD si [NQ] linie mijlocie in triunghiul BCD"
in sfarsit r1, r2, r3 se deduc imediat din p.
Schematic: 
Redactarea solutiei in mod natural:
In triunghiurile BAC si DAC care au latura comuna [AC] sunt puse in evidenta liniile mijlocii [KQ] si [LP], care corespund laturii comune.
Deci: KQ║LP si KQ = LP Analog: KN║LM si KN = LM
MP║NQ si MP = NQ
Rezulta ca patrulaterele KQLP, KNLM, MPNQ sunt paralelograme si mai mult cele trei bimediane [KL], [QP], [MN] ale tetraedrului sunt diagonale in aceste paralelograme : [KL] si [QP] in paralelogramul KQLP
[KL] si [MN] in paralelogramul KNLM
[MN] si [PQ] in paralelogramul MPNQ.
Cum diagonalele unui paralelogram sunt concurente si se injumatatesc, cele trei bimediane [KL], [QP], [MN] ale tetraedrului ABCD sunt concurente, punctul de concurenta este notat cu G - care este mijlocul fiecarei bimediane.
A3 Metoda reducerii la absurd.
Orice
teorema este o implicatie logica ![]() . Teorema reciproca fiind
. Teorema reciproca fiind ![]() .
.
Folosind tablele de
adevar, se demonstreaza ca teorema directa ![]() este echivalenta cu contrara teoremei reciproce q p.
este echivalenta cu contrara teoremei reciproce q p.
Echivalenta logica dintre teorema directa si contrara reciprocei se numeste principiul contrapozitiei.
Metoda
reducerii la absurd consta in: avand de demonstrat implicatia ![]() se admite ca nu este adevarata propozitia
q (se neaga concluzia q) si atunci, evident, ar fi
adevarata q. Folosind
si ipoteza p, pe baza unor deduceri logice, se ajunge la o absurditate,
care contravine fie ipotezei, fie unui adevar evident, fie unui
adevar stabilit anterior. Contradictia obtinuta atesta
valabilitatea teoremei directe
se admite ca nu este adevarata propozitia
q (se neaga concluzia q) si atunci, evident, ar fi
adevarata q. Folosind
si ipoteza p, pe baza unor deduceri logice, se ajunge la o absurditate,
care contravine fie ipotezei, fie unui adevar evident, fie unui
adevar stabilit anterior. Contradictia obtinuta atesta
valabilitatea teoremei directe ![]() .
.
Problema: (Reciproca teoremei lui Menelaus)
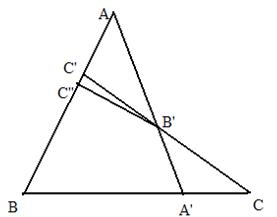
Consideram un triunghi ABC si punctele
A I (BC), B I (CA) si C I (AB).
Se presupune ca doua dintre puncte
sunt situate pe doua laturi ale triunghiului si
unul este situat pe prelungire celei de-a treia
latura (sau ca punctele A', B', C' sunt situate
pe prelungirile laturilor triunghiului).
Daca are loc egalitatea:
![]() (1)
(1)
atunci punctele A', B', C' sunt coliniare.
Demonstratie:
Presupunem ca doua dintre puncte sunt situate pe doua laturi ale triunghiului si unul este situat pe prelungire celei de-a treia latura.
Presupunem ca punctele A', B', C' nu sunt coliniare.
Atunci dreapta A'B' ar intersecta latura AB intr-un punct C" diferit de C'
Aplicand teorema lui Menelaus pentru punctele coliniare A', B', C" obtinem:
![]() (2)
(2)
Din relatiile (1) si (2) rezulta
ca: ![]()
Ar insemna ca segmentul [AB] este impartit de punctele interioare C' si C" in acelasi raport - contradictie, eliminand presupunerea facuta ajungem la concluzia ca punctele A', B', C' sunt coliniare.
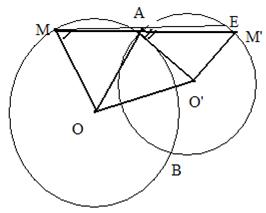 Problema:
Problema:
Se dau cercurile ![]() si
si ![]()
care se intersecteaza in punctele A si B.
De aceeasi parte cu A fata de dreapta OO'
se considera punctele ![]() si
si ![]()
astfel ca OM║O'A si O'M'║OA
Sa se arate ca punctele A, M, M' sunt coliniare.
Demonstratie:
Presupunem ca punctele A, M, M' nu sunt coliniare.
Fie E al doilea punct de intersectie al dreptei MA
cu cercul ![]()
Atunci: ![]() (1) ca unghiuri corespondente.
(1) ca unghiuri corespondente. ![]()
Unghiurile < MOA, < AO'M' - avand laturile doua cate doua paralele si de acelasi sens, sunt congruente.
Triunghiurile isoscele D MOA si D AO'M' sunt asemenea si atunci:
< AMO s < M'AO'
Comparand relatiile (1) si (2) obtinem ca: < EAO' s < M'AO' (3)
Din relatia (3) rezulta ca doua unghiuri cu varful comun in A, cu latura comuna [AO'] si cu interioarele de aceeasi parte a laturii commune sunt congruente fara ca celelalte doua laturi [AE, [AM' sa coincida.
Contradictia la care s-a ajuns arata ca punctele A, M, M' sunt coliniare.
B. Metode specifice de rezolvare a problemelor de coliniaritate si concurenta:
B1 - Cu ajutorul unicitatii paralelei
" Daca dreptele XY si XZ sunt paralele unei drepte d atunci punctele X, Y, Z sunt coliniare".
Problema: Fie B', C' mijloacele segmentelor (AC) respectiv (AB). D - simetricul lui B fata de B', iar E - simetricul lui C fata de C'.
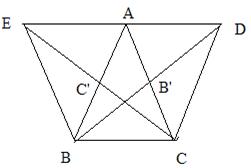 Sa se demonstreze ca
punctele D, A, E - sunt coliniare.
Sa se demonstreze ca
punctele D, A, E - sunt coliniare.
Demonstratie:
Patrulaterul AEBC avand diagonalele care se
taie in parti congruente este un paralelogram, deci:
(1) AE║BC
In patrulaterul ABCD diagonalele se taie in parti
congruente deci este un paralelogram, atunci:
(2) AD║BC
Din relatiile (1) si (2), tinand cont de axioma unicitatii paralelei rezulta ca punctele D, A, E - sunt coliniare.
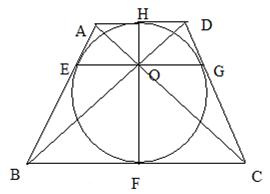 Problema:
Problema:
Trapezul isoscel ABCD (BC║AD) este
circumscris unui cerc de centru O. Punctele de contact
ale laturilor (AB), (BC), (CD), (DA) cu cercul inscris
sunt: E, F, G, H.
Diagonalele trapezului se intersecteaza in O.
Demonstrati ca E, O, G si H, O, F sunt
triplete de puncte coliniare.
Demonstratie:
Tinand cont ca trapezul ABCD este isoscel si este circumscris unui cerc avem egalitatile: (EB)=(BF)=(FC)=(CG) si (EA)=(AH)=(HD)=(DG)
Din asemanarea triunghiurilor formate
obtinem ca: ![]()
Aplicand reciproca teoremei lui Thales
din triunghiul D BAD obtinem EO║AD (1)
iar din triunghiul D DAC obtinem OG║AD (2)
Din relatiile (1) si (2), tinand cont de axioma unicitatii paralelei rezulta ca punctele E, O, G sunt coliniare.
Din OH AD, OF BC si AD║BC obtinem ca punctele H. O, F sunt coliniare.
B2 - Cu ajutorul ughiurilor adiacente suplementare
 "Daca
m(yxu)+m(uxz)=180
si punctele Y si Z sunt separate de dreapta XU, atunci punctele X, Y,
Z sunt coliniare"
"Daca
m(yxu)+m(uxz)=180
si punctele Y si Z sunt separate de dreapta XU, atunci punctele X, Y,
Z sunt coliniare"
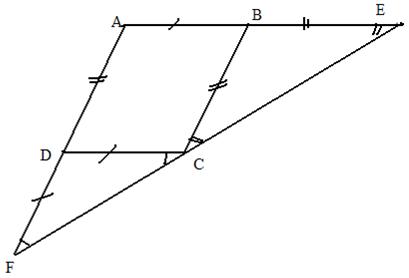
Problema:
Fie un paralelogram ABCD si
punctele E, F astfel incat
BI(AE), BE=AD, DI(AF), DF=AB.
Sa se demonstreze ca punctele
E, C, F sunt coliniare.
Demonstratie:
Din triunghiurile isoscele
D CBE si D FDC obtinem
relatiile: (1) <BCE s<CEB
(2) <DCF s<CFD
iar din paralelogramul ABCD obtinem (3) <DAB s<DCB
Tinand cont de relatiile (1), (2) si (3) rezulta: m(FCD)+m(DCB)+m(BCE)=180
Cum punctele D, F si E, B sunt de aceeasi parte a lui AC, rezulta ca punctele F, E sunt de o parte si de alta a dreptei AC, deci CI(FE).
Unghiurile ACF si ACE sunt adiacente suplementare daca laturile lor necomune vor fi in prelungire. Asadar punctele F, C, E - sunt coliniare.
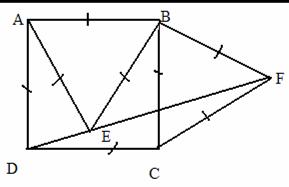 B3 -
"Daca < UXY s < UXZ si
punctele Y si Z de aceeasi parte a dreptei ux, atunci punctele X, Y,
Z - sunt coliniare".
B3 -
"Daca < UXY s < UXZ si
punctele Y si Z de aceeasi parte a dreptei ux, atunci punctele X, Y,
Z - sunt coliniare".
Problema:
Fie E un punct in interiorul patratului
ABCD si F un punct in exteriorul patratului
astfel incat triunghiurile D ABE si D BCF sa
fie truinghiuri echilaterale.
Demonstrati ca punctele
D, E, F - sunt coliniare
Demonstratie:
Va trebui sa demonstram ca < CDE s < CDF in conditia in care punctele E si F sunt de aceeasi parte a dreptei DC.
Din tiunghiul isoscel D ADE obtinem ca m(DAE)=30 , m(ADE)=m(AED)=75 ![]() Cum m(ADE) < m(ADC) T E si A sunt de aceeasi parte a lui
DC si m(CDE)=15
Cum m(ADE) < m(ADC) T E si A sunt de aceeasi parte a lui
DC si m(CDE)=15
Din triunghiul isoscel D DCF avem m(DCF) = 90 si
m(CDF) = m(CFD) = 15 cu punctele F si B de aceeasi parte a lui DC.
Cum punctele E si A respectiv F si B sunt de aceeasi parte a dreptei DC si
< CDE s < CDF obtinem ca punctele D, E, F - sunt coliniare.
B4 - Cu ajutorul reciprocei teoremei unghiurilor opuse la varf:
Fie dreapta UV, punctul XI(UV) si punctele Y si Z separate de dreapta UV.
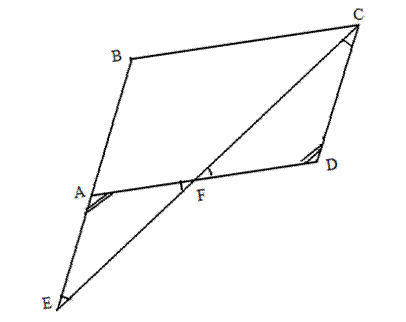 Daca < YXV s < UXZ, atunci punctele X,
Y, Z sunt coliniare.
Daca < YXV s < UXZ, atunci punctele X,
Y, Z sunt coliniare.
Problema:
Fie paralelogramul ABCD (AB<AD) si
punctele E, F astfel incat AI(BE), FI(AD)
si [BE]s[AD] si [DF]s[AB].
Demonstrati ca punctele C, F, E - sunt coliniare.
Demonstratie:
Unim F cu C si separat F cu E.
Triunghiurile D CDF si D AEF - isoscele.
Deoarece < EAFs< FDC
obtinem ca < AFEs< DFC.
Deoarece semidreptele [FE si [FC formeaza cu dreapta AD, FI(AD), de o parte si de alta a ei, unghiurile congruente < AFE si < DFC, rezulta ca semidreptele [FE si [FC sunt in prelungire, adica punctele E, F, C sunt coliniare.
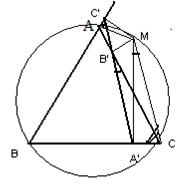 Problema: Dreapta lui Simson
Problema: Dreapta lui Simson
Sa se demonstreze ca proiectiile ortogonale ale unui
punct M de pe cercul circumscris unui triunghi pe laturile
acestuia sunt puncte coliniare.
Demonstratie
Fie A' = prBC M, B' = prAC M, C' = prAB M
Unim B' cu A' si separat B' cu C'
Patrulaterele ABCM, A'CMB', AB'MC' sunt inscriptibile.
Avem m(A'B'C)=m(A'MC)=90 - m(A'CM)=90 - m(C'AM)=m(C'MA)=m(C'B'A) deci < A'B'C = < C'B'A T punctele A', B', C' - sunt puncte coliniare.
B5 - Cu ajutorul reciprocei teoremei lui Simson:
Problema:
Fie H - ortocentrul triunghiului ABC si A' - piciorul inaltimii din A.
Se noteaza cu D - simetricul lui H fata de A' si fie E = prABD, F = prACD.
Sa se demonstreze ca punctele E, A' si F - sunt coliniare.
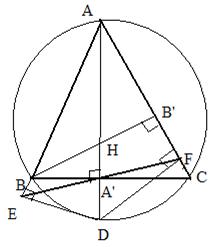
Demonstratie:
Din Teorema lui Simson, stim ca simetricul
ortocentrului unui triunghi se afla pe cercul
circumscris triunghiului.
Punctele A', E, F sunt proiectiile unui punct D
de pe cercul circumscris triunghiului ABC pe laturile
acestuia.
Conform teoremei lui Simson, punctele
A', F si E sunt puncte de pe dreapta lui Simson
a punctului D in raport cu triunghiul ABC.
Fiind pe aceeasi dreapta, punctele A', F si E sunt puncte coliniare.
B6 - Cu ajutorul reciprocei teoremei lui Menelaus:
Consideram triunghiul ABC - triunghi neisoscel.
Bisectoarea exterioara a unghiului A intersecteaza dreapta BC in A'
Analog Bisectoarea exterioara a unghiului B intersecteaza dreapta AC in B'
Bisectoarea exterioara a unghiului C intersecteaza dreapta AB in C'
Sa se arate ca punctele A', B', C' - sunt coliniare
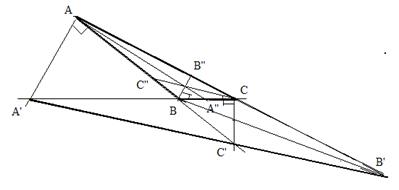
Stim ca bisectoarea interioara este perpendiculara pe bisectoarea exterioara.
AA" AA'
BB" BB'
CC" CC'
Notam: AB=c, AC=b, BC=a,
Din teorema bisectoarei unghiurilor exteriore A, B, C
avem: < A : ![]() (1) < B :
(1) < B : ![]() (2) si < C :
(2) si < C : ![]() (3)
(3)
Inmultind cele trei relatii membru cu membru, obtinem:
![]() si folosind reciproca teoremei lui Menelaus pentru
triunghiul ABC si punctele A', B', C' situate pe prelungirile laturilor
triunghiului obtinem ca punctele A', B', C' sunt coliniare.
si folosind reciproca teoremei lui Menelaus pentru
triunghiul ABC si punctele A', B', C' situate pe prelungirile laturilor
triunghiului obtinem ca punctele A', B', C' sunt coliniare.
B7 - Cu ajutorul identificarii unei drepte ce contine punctele X, Y, Z.
Problema:
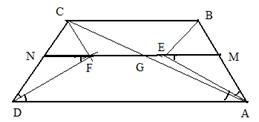 Fie trapezul isoscel ABCD (BC║AD).
Fie trapezul isoscel ABCD (BC║AD).
Bisectoarele interioare ale unghiurilor
A si B se intalnesc in E,
iar bisectoarele interioare
ale unghiurilor C si D in F.
Fie G mijlocul diagonalei AC.
Sa se arate ca punctele F, G, E sunt coliniare.
Demonstratie:
Triunghiul AEB este dreptunghic in E.
Fie M - mijlocul laturii AB, atunci
EM = ![]() AB, triunghiul EMA este isoscel.
AB, triunghiul EMA este isoscel.
< MEA s < MAE s <EAD, deci ME ║ AD.
Analog, pentru N - mijlocul lui CD, obtinem NE ║ AD
MN - fiind linie mijlocie in trapez, avem MN ║ AD, deci punctele E, F I MN.
G - mijlocul diagonalei apartine lui MN, asadar punctele F, G, E - sunt coliniare.
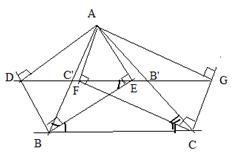 Problema:
Problema:
Fie un triunghi ABC si punctele
D, E, F, G - picioarele perpendicularelor duse
din A pe bisectoarele interioare si exterioare ale
unghiurilor < ABC, respectiv < ACB.
Sa se demonstreze ca punctele D, E, F, G
sunt coliniare.
Fie D, E, proiectiile lui A pe bisectoarele
unghiului ABC. ADBE - dreptunghi, deci DE trece prin C' - mijlocul diagonalei AB.
Din m(C'EB) = m(ABE) = ![]() m(B) = m(EBC), obtinem ca EC'║BC
m(B) = m(EBC), obtinem ca EC'║BC
Paralela prin C' la BC trece prin B' - mijlocul laturii AC.
Prin urmare punctele D, E, F, G apartin lui B'C', deci sunt coliniare.
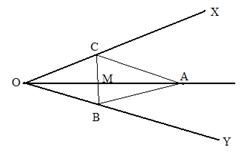 B8 - Cu ajutorul proprietatilor
paralelogramului:
B8 - Cu ajutorul proprietatilor
paralelogramului:
Problema:
Fie unghiul XOY si M un punct in interiorul lui,
nesituat pe nici una din laturi.
Segmentul [OM] se prelungeste cu [MA]s[OM].
Paralela prin A la OX intalneste pe OY in B, iar
paralela prin A la OY intalneste pe OX in C.
Sa se demonstreze ca punctele B, M, C - sunt coliniare.
Demonstratie:
In patrulaterul OBAC avem OC║AB, OB║AC, deci OBCA este paralelogram.
Segmentul [OA] - este una din diagonale, cu M - mijlocul ei.
Cealalta diagonala [BC] intersectaza diagonala [OA] in M.
Asadar punctele B, M si C sunt coliniare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 4580
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved