| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
NOTIUNI PRIVIND TEORIA ERORILOR DE MASURARE
1 Tipuri de masuratori
In topografie se executa masuratori asupra a doua tipuri de marimi fizice si anume distantele si unghiurile. in practica valoarea numerica a unei marimi masurata este cunoscuta numai aproximativ, indiferent de calitatea masuratorii efectuate.
In functie de modul de determinare a valorii numerice a unei marimi fizice exista trei tipuri de masuratori:
1. Masuratori directe - sunt acele masuratori la care valoarea marimii masurate rezulta direct si independent din compararea acestei marimi cu una asemanatoare. De exemplu masurarea distantei intre doua punct situate pe teren, cu ajutorul unei rulete este o masuratoare de tip direct.
2. Masuratori indirecte presupun masurarea directa a unor marimi care sunt legate printr-o relatie fizico-matematica de marimea a carei valoare se doreste a fi determinata. Spre exemplu, daca se doreste determinarea proiectiei, D, in plan orizontal, a distantei inclinate, L, intre doua puncte situate pe teren in panta, este necesar sa se masoare in mod direct valoarea L a distantei inclinate si unghiul de inclinare, fata de orizontala, j sau fata de verticala, V, a segmentului cuprins intre cele doua puncte. In acest caz valoarea cautata, D va rezulta din relatia sa geometrica cu cele doua elemente masurate:
D = L cosj
sau
D = L sin V
In mod asemanator, viteza rectilinie uniforma a unui mobil se poate determina prin masurarea directa a spatiului parcurs si a timpului necesar si prin efectuarea raportului celor doua valori.
Masuratori conditionate reprezinta un caz particular al masuratorilor directe, in care mai multe marimi de aceeasi natura sunt masurate direct si independent, dar intre ele exista o relatie de conditionare. Un exemplu concludent in acest sens il constituie cazul masurarii celor trei unghiuri intr-un triunghi situat in plan orizontal. Dupa masurarea directa si independenta a acestora, suma lor trebuie sa satisfaca conditia de egalitate cu valoarea a doua unghiuri drepte (180 sau 200g).
In general, rezultatul unei masuratori depinde de conditiile obiective si subiective in care se desfasoara aceasta, adica de metoda de masurare, de conditiile naturale (temperatura, presiune etc), calitatea aparaturii si de operatorul care o executa.
Daca se efectueaza mai multe masuratori asupra aceleiasi marimi si conditiile aratate mai sus nu se modifica, aceste masuratori au acelasi grad de incredere si se numesc masuratori de aceeasi precizie.
Daca la efectuarea sirului de masuratori se modifica unul din factorii enumerati atunci rezultatele vor avea grade diferite de incredere iar masuratorile sunt de precizii diferite.
Indiferent de situatie rezultatele unui sir de masuratori asupra aceleiasi marimi sunt in general diferite datorita erorilor acestui proces.
2 Tipuri de erori de masurare
Calitatea rezultatului, x, al unei masuratori se apreciaza in functie de abaterea, e a acestuia fata de valoarea reala, X a marimii masurate. Aceasta abatere data de:
e = xi - X
se numeste eroare absoluta a rezultatului masuratorii. Cu cat eroarea absoluta este mai mica cu atat masuratoarea este mai precisa.
In masuratorile obisnuite, valoarea reala a marimii nu se cunoaste, deci nici eroarea absoluta a rezultatului nu este cunoscuta. Chiar daca erorile absolute nu pot fi definite prin valoarea lor, studiul rezultatelor unui sir de masuratori permite aprecierea - cu un anumit grad de certitudine - a marimii acestora. In functie de marimea erorilor si de modul lor de producere se deosebesc:
1. Erori grave acestea conduc la rezultate foarte diferite fata de majoritatea rezultatelor din sirul de masuratori. Ele se produc datorita unor cauze subiective cum sunt de exemplu greselile de citire. In general rezultatele afectate de erori grave se elimina din sirul respectiv.
2. Erori sistematice sunt generate de cauze obiective cum ar fi de exemplu, metoda de masurare utilizata, etalonarea aparatului de masura, temperatura diferita in momentul masurarii fata de cel al etalonarii etc. Aceste erori conduc la rezultate deplasate in acelasi sens si cu valori apropiate fata de valoarea reala a marimii masurate. Deoarece conditiile care au generat aceste erori pot fi evaluate, erorile sistematice pot fi in general eliminate prin aplicarea unor corectii la rezultatele masuratorilor.
3. Erori aleatoare rezulta datorita unor factori obiectivi sau subiectivi imposibil de evaluat in timpul masuratorii, dar aceste erori au valori foarte reduse. Ele nu pot fi eliminate si afecteaza rezultatul masurarii, constituind subiectul operatiilor de compensare. Deoarece erorile in procesul de masurare sunt inevitabile, o singura masuratoare aspra unei marimi nu permite sa se aprecieze gradul de calitate al rezultatului. Din acest motiv, pentru masuratorile pretentioase se executa mai multe masuratori (un sir) asupra marimii. Dintr-un sir de n masuratori asupra unei marimi reale X, rezulta valorile determinate x1 ,x2, xn. Se pot deci scrie n ecuatii ale erorilor absolute de forma ei = xi - X, iar numarul necunoscutelor este n + l, deoarece marimea X este necunoscuta. Rezulta ca problema determinarii valorii reale X este nerezolvabila, insa datorita faptului ca erorile aleatoare rezultate din observatii se supun unor legi cunoscute, exista posibilitatea determinarii unei valori acceptabile, apropiata de valoarea reala, si a preciziei acesteia.
3 Estimari ale adevaratei valori a unei marimi masurate
Se considera o marime a carei valoare reala este X si un sir de n valori ale masuratorilor efectuate asupra acestei marimi, avand rezultatele x1,x2 xn. Se considera ca au fost eliminate rezultatele care au continut erori grave, iar erorile sistematice au fost corectate, deci cele n valori sunt afectate doar de erori aleatoare.
Deoarece valoarea reala, X nu poate fi determinata cu certitudine se procedeaza la estimarea acesteia, adica la gasirea unei valori foarte apropiate, prin prelucrarea rezultatelor masuratorilor. Aceasta estimare se poate face in doua moduri:
a) Printr-o valoare unica data de o functie f(x1,x2,,xn) a rezultatelor din sirul de masuratori. In acest caz estimatia se numeste punctuala.
b) Prin determinarea unui interval (a - Dx, a Dx) in care valoarea reala sa se gaseasca cu o probabilitate P, numita nivel de incredere. In acest caz este vorba de o estimare printr-un interval de incredere.
In masuratorile topografice se utilizeaza in mod frecvent estimatia punctuala a adevaratei valori a marimii masurate, prin media aritmetica a sirului de masuratori. Astfel, pentru masuratori de egala precizie, valoarea estimata este media aritmetica a sirului de masuratori:
 (4)
(4)
In
teoria erorilor se spune ca aceasta estimatie este
nedeplasata, adica valoarea ![]() coincide cu media teoretica a sirului, si, consistenta,
ceea ce inseamna ca aceasta tinde catre valoarea reala X,
in cazul cand numarul n de
masuratori creste.
coincide cu media teoretica a sirului, si, consistenta,
ceea ce inseamna ca aceasta tinde catre valoarea reala X,
in cazul cand numarul n de
masuratori creste.
In cazul cand masuratorile efectuate au precizii diferite, atunci fiecareia i se atribuie o pondere p1,p2,,pn, iar estimarea punctuala a adevaratei valori se va exprima prin media ponderata:
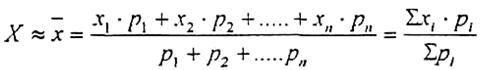 (5)
(5)
Aceasta estimatie punctuala are aceleasi proprietati ca si precedenta iar valoarea determinata nu depinde de ponderi ci de raportul acestora.
Asa
cum s-a aratat, erorile absolute nu pot fi cunoscute deoarece nu se
cunoaste valoarea reala ci doar estimarea acesteia. In
legatura cu media aritmetica se pot insa defini erorile
aparente, ca diferenta intre
valorile rezultate din masuratori xi, si valoarea
estimarii punctuale (media aritmetica),
![]()
![]()
![]()
![]()
Erorile aparente sunt asemanatoare cu cele aleatoare si au doua proprietati importante:
- suma lor algebrica este nula:
![]()
- suma patratelor erorilor aparente admite ca minim valoarea de referinta, adica media aritmetica
![]()
Dupa derivarea expresiei (8) si egalarea cu zero se obtine:
![]()
de unde:
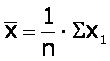
4 Repartitia normala a erorilor aparente
Studiul efectuat de C.F.Gauss asupra
erorilor de observatie aleatoare a condus la concluzia ca acestea sunt caracterizate de o
functie de repartitie. Daca pentru un sir suficient de
lung de masuratori, x1, x2, ,xn se reprezinta - intr-un sistem cartezian - pe
axa absciselor valorile erorilor, iar
pe axa ordonatelor numarul de masuratori in care au rezultat
aceleasi valori ale erorilor respective (sau
probabilitatile de aparitie a acestor erori) se obtine o
multime de puncte care sunt dispuse
sub o curba asemanatoare celei din fig. 1. Aceasta se
numeste curba repartitiei normale a erorilor,
a lui Gauss. Daca se
considera valoarea medie a celor n masuratori, ![]() si
erorile aparente de forma (6.6),
atunci functia care defineste aceasta curba este de forma:
si
erorile aparente de forma (6.6),
atunci functia care defineste aceasta curba este de forma:
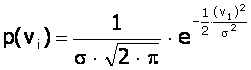 (11)
(11)
Aceasta functie are un maxim pentru vi =0 si puncte de inflexiune pentru vi= s
Factorul s se numeste factor de precizie sau eroarea medie patratica a unei singure masuratori si a fost definit de Bessel pentru masuratori directe de aceeasi precizie sub forma:
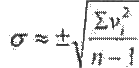
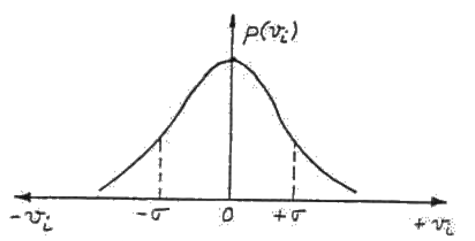
Fig. 1 Curba Gauss de repartitie normala a erorilor aparente
Cu cat factorul s este mai mic, cu atat maximul curbei este mai mare, ceea ce inseamna ca precizia estimatiei este mai mare (fig. 2).
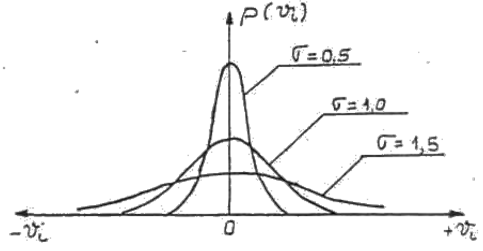
Fig. 2 Forma curbei Gauss in functie de factorul de precizie
Forma curbei lui Gauss conduce la cateva concluzii importante:
- masuratorile cu erori negative sunt la fel de frecvente ca si cele cu erori pozitive;
- masuratorile cu erori mici sunt mai frecvente decat cele cu erori mari;
- practic, erorile maxime nu pot depasi o anumita limita;
- media aritmetica a erorilor tinde la zero pentru un numar mare de masuratori.
Functia p(vi) permite stabilirea unui interval de forma ls ls in care o anumita eroare se poate situa, cu un grad de probabilitate P.
Tabel 1 - Valori ale limitelor de interval si probabilitatea ca eroarea sa fie in acest interval
|
Valoare interval |
s |
s |
l.96s |
s |
s |
s |
|
Probabilitate (%) |
Din tabelul 1 rezulta ca se poale realiza o estimare a valorii unei erori printr-un interval de incredere. Spre exemplu, se poate estima ca la un grad de incredere P=50% eroarea unei masuratori va fi cuprinsa in intervalul (-0,67s s Valoarea 0,67s se numeste eroarea probabila iar valoarea l . s se numeste eroarea medie a masuratorii.
5 Eroarea medie a mediei aritmetice
S-a aratat ca
pentru un sir de masuratori de aceeasi precizie x1,
x2 xn estimarea punctuala presupune gasirea unei valori y = f(x1, x2 xn),
considerata ca valoare probabila a rezultatului masuratorii. Considerand ca erorile
masuratorilor raportate la estimarea punctuala prin media aritmetica, ![]() sunt v1, v2,vn,
atunci conform legii lui Gauss a propagarii erorilor, eroarea medie patratica
a estimatiei punctuale (deci a mediei
aritmetice) are forma:
sunt v1, v2,vn,
atunci conform legii lui Gauss a propagarii erorilor, eroarea medie patratica
a estimatiei punctuale (deci a mediei
aritmetice) are forma:
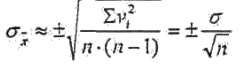
unde s este eroarea medie patratica a unei masuratori iar n - numarul de masuratori din sir.
Cu ajutorul valorii s se poate stabili un
interval de forma ![]() in care valoarea estimata a rezultatelor
masuratorii se afla cu un grad de probabilitate P. Valoarea
l care caracterizeaza
intervalul poate fi aleasa astfel incat sa se obtina o
limita minima de incredere sau, una
tolerabila, a valorii estimate fata de valoarea reala a
marimii masurate.
in care valoarea estimata a rezultatelor
masuratorii se afla cu un grad de probabilitate P. Valoarea
l care caracterizeaza
intervalul poate fi aleasa astfel incat sa se obtina o
limita minima de incredere sau, una
tolerabila, a valorii estimate fata de valoarea reala a
marimii masurate.
Trebuie specificat ca erorile observatiilor nu au repartitie normala pentru orice tip de masuratori, deci exista si alte tipuri de repartitie pentru care relatiile de mai sus nu mai sunt valabile. Spre exemplu, erorile datorate centrarii limbului, la masurarea unghiurilor orizontale cu ajutorul tahimetrelor, urmeaza o lege de distributie parabolica.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2154
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved