| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
SISTEME DE ECUATII LINIARE SI CONVEXITATE IN Rn
Obiective : insusirea de catre studenti a metodelor de rezolvare exacta si aproximativa a sistemelor de ecuatii liniare cu aplicatii in operatii cu poliname,a convexitatii multimii solutiilor unui sistem liniar compatibil nedeterminat si a extremelor unui polinom convex/concav pe aceasta multime.
Continut :
1 Sisteme de ecuatii liniare si aplicatii
1.1 Rezolvarea si discutia unui sistem de ecuatii liniare
1.2 Rezolvarea sistemelor liniare compatibile determinate
1.3 Aplicarea sistemelor liniare la operatii cu polinoame si algoritmul lui Euclid
1.4 Metode iterative de rezolvare a sistemelor liniare
1.5 Solutii generalizate ale sistemelor liniare incompatibile
2 Multimi convexe pe Rn
3 Extremele unui polinom convex/concav pe o multime convexa din Rn
4 Rezumat
5 Intrebari
6 Bibliografie
Cuvinte cheie : solutie generala si solutie particulara bazica a unui sistem liniar,sisteme
tridiagonale,erori in rezolvarea sistemelor liniare,solutie generalizata a unui sistem liniar incompatibil,multimi convexe si polinoame concave/convexe ,solutii bazice(extremale)
si optime .
1 Sisteme de ecuatii liniare si aplicatii
1.1 Rezolvarea si discutia unui sistem liniar
Fie sistemul liniar de m ecuatii cu n necunoscute, de forma:
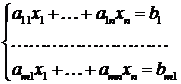 . Cu notatiile:
. Cu notatiile: 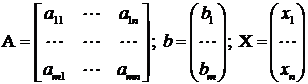
avem forma matriciala a sistemului: AX=b
Fie ![]() . Presupunem ca minorul
principal ocupa primele r linii si primele r coloane.
. Presupunem ca minorul
principal ocupa primele r linii si primele r coloane.
Fie F submatricea minorului principal: 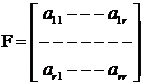 cu
cu ![]()
|
Avem |
|
unde G este submatrice de tip |
tip ![]() iar K este submatrice de tip
iar K este submatrice de tip
![]() .
.
|
Fie matricea extinsa de tip |
|
unde |
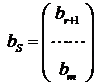 . Dupa pivotare in
matricea extinsa
. Dupa pivotare in
matricea extinsa ![]() , aceasta capata
forma:
, aceasta capata
forma:
|
|
unde |
Conform teoremei Kronecker-Capelli, sistemul
liniar este compatibil daca si numai daca ![]() .
.
CAZURI:
I) ![]()
Matricea ![]() este de tip
este de tip ![]() deci
deci ![]() si
cum
si
cum ![]() rezulta
rezulta ![]() deci
sistemul este compatibil. Daca
deci
sistemul este compatibil. Daca ![]() , sistemul este compatibil
determinat iar daca
, sistemul este compatibil
determinat iar daca ![]() , sistemul este compatibil
nedeterminat.
, sistemul este compatibil
nedeterminat.
II) ![]()
Subcazul a)
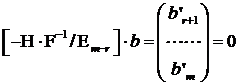
adica b este ortogonal pe Ker(AT)
deci ![]() .
Rezulta
.
Rezulta ![]() deci sistemul este compabil
(determinat pentru
deci sistemul este compabil
(determinat pentru ![]() si
nedeterminat pentru
si
nedeterminat pentru ![]() ).
).
In acest caz ultimele ![]() linii secundare
din matricea extinsa
linii secundare
din matricea extinsa ![]() se arunca fiind
dependente de primele r linii principale. Avem:
se arunca fiind
dependente de primele r linii principale. Avem:
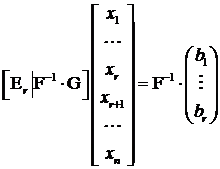 adica
adica 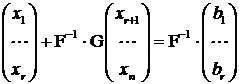 de unde:
de unde:
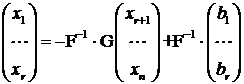 si
completand cu necunoscutele secundare
si
completand cu necunoscutele secundare ![]() , obtinem:
, obtinem:
(1) 
Matricea 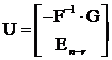 este de tip
este de tip ![]() si
si ![]() .
Coloanele sale Ur+1,.,Un IRn sunt solutii liniar independente ale sistemului omogen
.
Coloanele sale Ur+1,.,Un IRn sunt solutii liniar independente ale sistemului omogen ![]() . Aceste
coloane formeaza o baza in subspatiul Ker(A) Rn cu
. Aceste
coloane formeaza o baza in subspatiul Ker(A) Rn cu ![]() .
.
Coloana 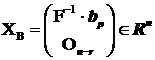 este o
solutie particulara bazica (vezi sectiunea 2) a sistemului
liniar neomogen
este o
solutie particulara bazica (vezi sectiunea 2) a sistemului
liniar neomogen![]() . Ea se obtine din
solutia generala a sistemului neomogen pentru componentele nebazice
nule
. Ea se obtine din
solutia generala a sistemului neomogen pentru componentele nebazice
nule ![]() .
Cu notatiile precedente, solutia generala din relatia (1)
are forma:
.
Cu notatiile precedente, solutia generala din relatia (1)
are forma:
![]() unde
unde 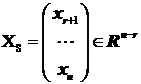
Solutia generala X(0) = U.XS a sistemului omogen AX=0 reprezinta ecuatiile parametrice ale subspatiului vectorial L atasat sistemului omogen AX=0 (vezi teorema 2.1) ,XS fiind vectorul celor n - r parametri reali xr+1,.,xn .
Solutia generala X=U.XS+XB a sistemului neomogen AX=b reprezinta ecuatiile parametrice ale varietatii liniare b + L ( b L) depinzand de aceiasi parametri reali xr+1,.,xn .
Exemple
Ecuatia planului in R3 are forma generala a11x + a12y+a13z+a14=0 .
Daca a11 0 ecuatia planului are forma parametrica :
x = ( - a12 / a11)y+( - a13 / a11 )z + ( - a14 / a11) ; y=y ; z =z cu parametrii reali y si z .
Ecuatiile dreptei in R3 au forma generala :
a11x +a12y+a13z +a14 =0
a21x+a22y+a23z+a24 =0
Daca D=a11a22 - a12a21 0 , din aceste ecuatii aflam pe x si y in functie de z :
x=a z+ b ; y=a z+ b ; z=z adica ecuatiile parametrice ale dreptei cu parametrul z .
Exista o solutie
particulara unica XNIRn sistemului liniar ![]() cu
cu ![]() , numita solutie
normala. Ea are propietatea ca este ortogonala pe
subspatiul liniar
, numita solutie
normala. Ea are propietatea ca este ortogonala pe
subspatiul liniar ![]() adica
adica ![]() deci XNIIm(AT) .
deci XNIIm(AT) .
Conform relatiei (2)
avem: ![]() deci:
deci:
![]() asa
ca:
asa
ca: ![]() . Rezulta din
relatia (2):
. Rezulta din
relatia (2): ![]() deci solutia
normala are forma:
deci solutia
normala are forma:
![]()
Subcazul b)
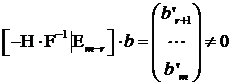 .
.
In acest caz cel putin o
componenta a vectorului-coloana: 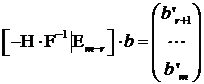
cu ![]() componente, este
nenula.
componente, este
nenula.
Fie de exemplu prima
componenta ![]() . In acest caz sistemul
liniar este incompatibil deoarece
. In acest caz sistemul
liniar este incompatibil deoarece ![]() cu minorul nenul de ordin
cu minorul nenul de ordin ![]() :
:

Discutia sistemului liniar este
terminata.
Spre deosebire de sistemul liniar ![]() care este
compatibil daca si numai daca
care este
compatibil daca si numai daca ![]() sau
sau ![]() , sistemul
, sistemul ![]() este
totdeauna compatibil si solutia sa
este
totdeauna compatibil si solutia sa ![]() se numeste solutie
generalizata a sistemului
se numeste solutie
generalizata a sistemului ![]() . Ea are
proprietatile:
. Ea are
proprietatile:
i) AX+ - b este ortogonal
pe Im(A) ; ii) ![]()
Daca
c este proiectia vectorului b pe subspatiul Im(A)
atunci ![]() este
solutie a sistemului compatibil
este
solutie a sistemului compatibil ![]() .Solutia (2) este
data de programul SISTEM .
.Solutia (2) este
data de programul SISTEM .
Exemplu
Se da sistemul liniar: 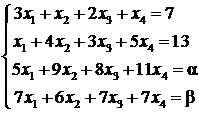
Sa se discute sistemul dupa ![]() si
daca este compatibil sa se rezolve sistemul.
si
daca este compatibil sa se rezolve sistemul.
Solutie
|
Baza |
A1 |
A2 |
A3 |
A4 |
b |
|
E1 |
3 |
1 |
2 |
1 |
7 |
|
E2 |
1 |
4 |
3 |
5 |
13 |
|
E3 |
5 |
9 |
8 |
11 |
α |
|
E4 |
7 |
6 |
7 |
7 |
b |
|
A1 |
1 |
|
|
|
|
|
E2 |
0 |
|
|
|
|
|
E3 |
0 |
|
|
|
|
|
E4 |
0 |
|
|
|
|
|
A1 |
1 |
0 |
|
|
|
|
A2 |
0 |
1 |
|
|
|
|
E3 |
0 |
0 |
0 |
0 |
|
|
E4 |
0 |
0 |
0 |
0 |
|
Discutie
Pentru ![]() sau
sau ![]() sistemul este
incompatibil. Pentru
sistemul este
incompatibil. Pentru ![]() si
si ![]() sistemul este
compatibil (nedeterminat caci
sistemul este
compatibil (nedeterminat caci ![]() ). Ecuatiile secundare a
treia si a patra se arunca. Ecuatiile principale a intiia
si a doua se scriu:
). Ecuatiile secundare a
treia si a patra se arunca. Ecuatiile principale a intiia
si a doua se scriu:
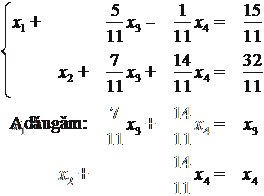
Solutia generala a sistemului neomogen este:
(4) 
Primii doi termeni din membrul doi
reprezinta solutia generala a sistemului omogen ![]() iar al
treilea termen este o solutie particulara bazica a sistemului
neomogen (obtinuta din solutia generala a sistemului
neomogen pentru
iar al
treilea termen este o solutie particulara bazica a sistemului
neomogen (obtinuta din solutia generala a sistemului
neomogen pentru ![]() ).
).
Coloanele principale ![]() din matricea A se
numesc bazice iar celelalte coloane secundare
din matricea A se
numesc bazice iar celelalte coloane secundare ![]() ca si
termenul liber b al sistemului se exprima cu ajutorul coloanelor
bazice
ca si
termenul liber b al sistemului se exprima cu ajutorul coloanelor
bazice ![]() :
:
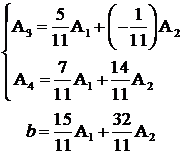
Din forma generala a solutiei X data de relatia (2) rezulta:
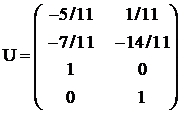 si
si
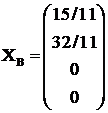
Conform relatiei (3) rezulta
solutia normala  cu
cu ![]() . Relatia (4)
se scrie si sub forma:
. Relatia (4)
se scrie si sub forma:
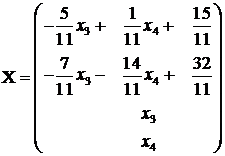
deci 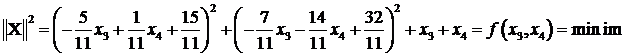
Trebuie sa avem:
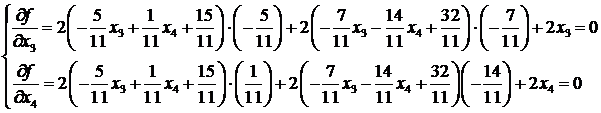
de unde rezulta ![]() ;
; ![]() deci
solutia normala:
deci
solutia normala: 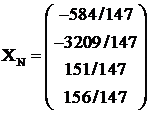 obtinuta si
mai sus cu relatia (3).
obtinuta si
mai sus cu relatia (3).
1.2 Sisteme liniare compatibile determinate particulare (m = n ;det(A)≠0)
a) Sisteme triunghiulare
Sistemele liniare superior-triunghiulare au forma A.X = b unde A este
matrice patratica nesingulara superior triunghiulara : aij = 0 pentru i>j .Solutia
acestor sisteme este data
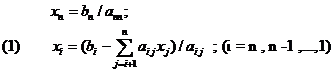 |
Sistemele liniare inferior-triunghiulare au forma A.X = b unde A este matrice patratica nesingulara inferior triunghiulara : aij =0 pentru i<j . Solutia acestor sisteme este data de relatiile :
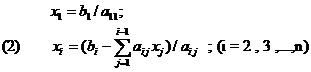 |
Sistemele liniare se pot rezolva prin descompunerea matricii A , urmata de reducerea rezolvarii sistemului liniar initial la rezolvarea a doua sisteme triunghiulare cu solutii de forma (1) sau (2) .
b) Descompunerea A = L.U
Daca matricea A are toti minorii principali ∆1 , ∆2 ,., ∆n nenuli , algoritmul Gauss realizeaza descompunerea A = L.U unde L su U sunt matrici patratice nesingulare : L este inferior-triunghiulara iar U este superior-triunghiulara .
Sistemul liniar A.X = b devine L.(U.X) = b deci cu notatia U.X = Y ,vom rezolva sistemul liniartriunghiular L.Y = b cu relatiile (2) apoi vom rezolva sistemul liniar triunghiular U.X = Y cu relatiile (1).
c). Descompunerea Cholesky A = B.BT
Daca A este matrice simetrica pozitiv definita (are toti minorii principali ∆1 , ∆2 ,., ∆n strict pozitivi , respectiv toate valorile proprii reale strict pozitive) atunci exista matricea patratica nesingulara de ordin n ,inferior triunghiulara astfec ca are loc descompunerea Cholesky A = B.BT conform relatiilor :
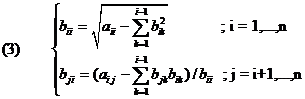
Sistemul liniar A.X = b devine B.(BT.X) = b deci cu notatia BT.X =Y , se rezolva sistemul liniar triunghiular B.Y = b in raport cu necunoscuta Y cu formulele (2) , apoi se rezolva sistemul liniar triunghiular BT.X = Y in raport cu necunoscuta X cu formulele (1).
d). Descompunerea A = Q.R
La ortonormalizarea unei baze din R n ai carei vectori-coloana A1,.,An formeaza matricea patratica nesindulara A de ordin n , se obtine descompunerea A = Q.R unde Q este matricea ortogonala ( Q-1 = QT) care are pe coloane versorii bazei ortonormale iar R este o matrice superior-triunghiulara nesingulara de ordin n .
Sistemul liniar A.X = b devine Q.(R.X) = b deci cu notatia R.X = Y , se rezolva sistemul liniar Q.Y = b in raport cu necunoscuta Y ,cu solutia Y = Q-1.b = QT.b apoi se rezolva sistemul triunghiular R.X = Y in raport cu necunoscuta X , cu formulele (1) .
e) Sisteme liniare tridiagonale
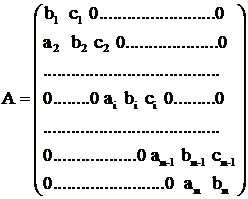 |
Descompunem matricea tridiagonala A in
produsul a doua matrici bidiagonale: ![]() unde:
unde:
 |
 |
Prin identificare obtinem relatiile:
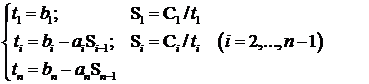
Descompunerea ![]() este posibila
daca
este posibila
daca ![]() .
.
Sistemul liniar ![]() devine
devine ![]() deci se reduce la
doua sisteme liniare cu matrici bidiagonale:
deci se reduce la
doua sisteme liniare cu matrici bidiagonale: ![]() si
si ![]() cu vectorii
necunoscutelor U,V IRn
cu vectorii
necunoscutelor U,V IRn
Sistemul liniar ![]() are solutiile:
are solutiile:
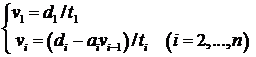
Sistemul liniar ![]() cu
componentele lui V date de relatiile (2), are solutiile:
cu
componentele lui V date de relatiile (2), are solutiile:
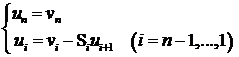
In concluzie, solutia U IRn a sistemului tridiagonal ![]() este data prin
aplicarea formulelor recurente (1) + (2) + (3) . Programul
TRIDIAG face aceste calcule.
este data prin
aplicarea formulelor recurente (1) + (2) + (3) . Programul
TRIDIAG face aceste calcule.
Exemplu
Sa se rezolve sistemul tridiagonal de
ordin 4: 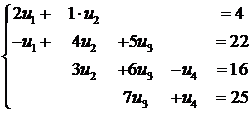
Solutie
Din relatiile (1) avem succesiv:
![]()
![]()
![]()
![]()
Din relatiile (2) avem succesiv: ![]()
Din relatiile (3) avem succesiv solutiile sistemului tridiagonal:
![]() .
.
1.3 Aplicarea sistemelor liniare la operatii cu polinoame
a) Inmultirea polinoamelor
Fie polinoamele: ![]() de grad m
si
de grad m
si ![]() de grad n. Produsul
de grad n. Produsul ![]() de grad
de grad ![]() are
are
forma:
![]()
Coeficientii ![]() se pot
obtine prin inmultirea unei matrici cu un vector-coloana.
Fie vectorul-coloana:
se pot
obtine prin inmultirea unei matrici cu un vector-coloana.
Fie vectorul-coloana: ![]() si fie matricea
patratica de ordin
si fie matricea
patratica de ordin ![]() :
:
Vectorul-coloana: ![]() se obtine din
produsul:
se obtine din
produsul:
C = A ∙ b
Exemplu
Fie polinoamele ![]() si
si ![]() de grade
de grade
![]() si
si
![]() .
Avem
.
Avem ![]() si
matricea:
si
matricea:
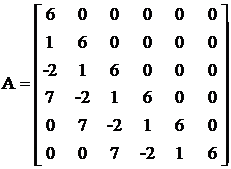
Vectorul ![]() se obtine din produsul:
se obtine din produsul:
![]() adica
adica
![]() deci
deci
![]() .
.
Programul POLINM face aceste calcule.
b) Impartirea polinoamelor
Fie polinoamele: ![]() de grad m
si
de grad m
si ![]() de grad n. In ipoteza
ca
de grad n. In ipoteza
ca ![]() prin
impartirea polinomului
prin
impartirea polinomului ![]() la polinomul
la polinomul ![]() se
obtine polinomul-cat:
se
obtine polinomul-cat: ![]() de grad
de grad ![]() si
polinomul-rest:
si
polinomul-rest: ![]() de grad
de grad ![]() . Avem
. Avem ![]() de unde:
de unde:
![]() .
.
Coeficientii ![]() se
obtin ca solutie a unui sistem liniar compatibil determinat.
Fie vectorul-coloana redus:
se
obtin ca solutie a unui sistem liniar compatibil determinat.
Fie vectorul-coloana redus: ![]() si fie matricea
patratica de ordin
si fie matricea
patratica de ordin ![]() redusa:
redusa:
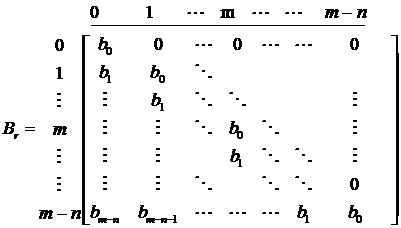
Vectorul-coloana redus:![]() se
obtine din ecuatia matriciala Brcr=ar
de unde:
se
obtine din ecuatia matriciala Brcr=ar
de unde:
![]()
Br-1 exista
deoarece ![]() . Restul
. Restul ![]() de grad
de grad ![]() se
obtine din relatia
se
obtine din relatia ![]() unde produsul
unde produsul ![]() se
obtine ca la punctul 1.:
se
obtine ca la punctul 1.:
Fie vectorul-coloana: ![]() , fie
matricea patratica de ordin
, fie
matricea patratica de ordin ![]() :
:
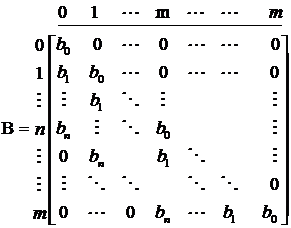
si fie vectorul-coloana: ![]()
Vectorul-coloana al restului este: ![]() si
este dat de relatia:
si
este dat de relatia:
(3) ![]()
Coeficientii restului sunt dati de
vectorul-coloana redus: ![]()
Exemplu
Fie polinoamele ![]() de grad
de grad ![]() si
si ![]() de grad
de grad ![]() .
.
Avem: ![]() si matricea
redusa:
si matricea
redusa: 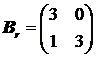 cu inversa
cu inversa 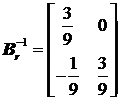
Rezulta din relatia (2): 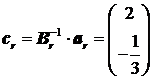 asa
ca
asa
ca ![]() .
.
Avem: ![]() precum si matricea de
ordin
precum si matricea de
ordin ![]() :
:
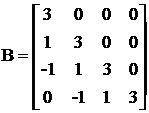
si vectorul-coloana 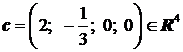
Din relatia (3) rezulta:
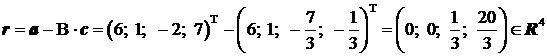
Vectorul redus 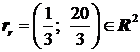 da coeficientii
restului
da coeficientii
restului ![]()
Programul POLIMP face aceste calcule.
c) Schema lui Horner
In particular daca avem
polinoamele: ![]() de grad m si
de grad m si ![]() de grad
de grad ![]() . Prin
impartirea lui
. Prin
impartirea lui ![]() cu
cu ![]() obtinem catul
de grad
obtinem catul
de grad ![]() :
:
![]() si
restul
si
restul ![]() de
grad
de
grad ![]() .
.
Din relatia:![]() prin
identificarea coeficientilor puterilor lui x din ambii membri,
obtinem relatiile de recurenta:
prin
identificarea coeficientilor puterilor lui x din ambii membri,
obtinem relatiile de recurenta:
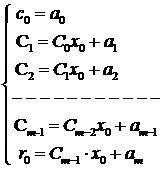
din care se obtine catul ![]() si
restul
si
restul ![]() .
.
Observam ca ![]() deci daca
deci daca ![]() avem
avem ![]() si
reciproc.
si
reciproc.
Relatiile de mai sus se constituie in schema lui Horner:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Programul HORNER face aceste calcule.
Algoritmul Euclid pentru polinoame
Algoritmul Euclid pentru polinoamele ![]() de grad m
si
de grad m
si ![]() de
grad
de
grad ![]() este:
este:
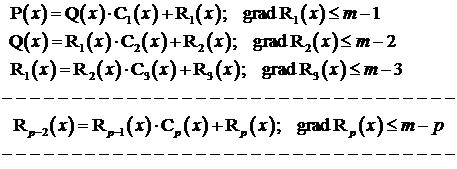
Cazuri
I. Exista
![]() cu
cu
![]() deci
deci
![]() este
cel mai mare divizor comun al polinoamelor
este
cel mai mare divizor comun al polinoamelor ![]() iar ecuatia
iar ecuatia ![]() da
radacinile comune ale polinoamelor
da
radacinile comune ale polinoamelor ![]() .
.
II. ![]() deci
deci ![]()
Programul EUCLID face aceste calcule.
Algoritmul Euclid aplicat
polinomului: ![]() si derivatei sale:
si derivatei sale: ![]() da
radacinile multiple ale lui
da
radacinile multiple ale lui ![]() . Radacina
. Radacina ![]() a lui
a lui ![]() este
de multiplicitate
este
de multiplicitate 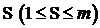 daca
daca ![]() dar
dar ![]() .
.
Exemplu
Se cer radacinile multiple ale
polinomului: ![]()
Solutie
Avem ![]()
Relatia ![]() implica:
implica: ![]()
Relatia ![]() implica:
implica: ![]() deci
deci ![]() este cel
mai mare divizor comun pentru
este cel
mai mare divizor comun pentru ![]() iar radacina
iar radacina ![]() a lui
a lui ![]() este
radacina multipla alui
este
radacina multipla alui ![]() . Avem
. Avem ![]() si
si ![]() asa
ca
asa
ca ![]() este
radacina dubla
este
radacina dubla ![]() .
.
1.4 Metode iterative de rezolvare a sistemelor liniare
Fie sistemul liniar de n
ecuatii cu n necunoscute, scris matricial ![]() . Presupunem
ca
. Presupunem
ca ![]() deci
sistemul este compatibil determinat. S-a prezentat ca metoda exacta
metoda substituirii unui vector din baza standard si ca o varianta
metoda matricii inverse:
deci
sistemul este compatibil determinat. S-a prezentat ca metoda exacta
metoda substituirii unui vector din baza standard si ca o varianta
metoda matricii inverse: ![]() .
.
Daca n este mare, erorile de rotunjire se pot acumula, dand erori mari ale solutiilor. Pentru cresterea preciziei, la sisteme mari se pot folosi metode iterative.
a) Metoda aproximatiilor succesive (Jacobi)
Fie sistemul liniar:
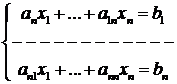 adus sub forma:
adus sub forma: 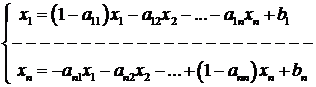
adica sub forma matriciala: 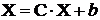 unde
unde ![]() . Valoarea
initiala a solutiei este
. Valoarea
initiala a solutiei este ![]() iar iteratiile sunt
date de relatia:
iar iteratiile sunt
date de relatia: ![]()
sau pe componente:
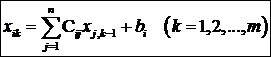
Se arata ca daca:
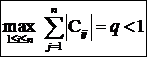
atunci sirul de vectori 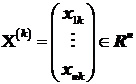 dat de
relatia (1) , este convergent catre solutia exacta
dat de
relatia (1) , este convergent catre solutia exacta 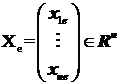 a
sistemului
a
sistemului ![]()
Fie norma vectorului 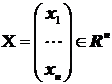 data
de relatia:
data
de relatia: ![]()
Eroarea antecalculata a procesului
iterativ din ecuatia (1) este: 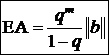 deoarece
deoarece
![]() .
.
Eroarea postcalculata a procesului
iterativ din ecuatia (1) este: 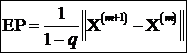 deoarece
deoarece
![]() .
.
Eroarea de verificare este ![]()
Exemplu
Fie sistemul liniar compatibil determinat: 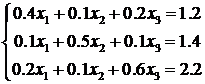
Aducem sistemul liniar la forma 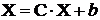 adica:
adica:
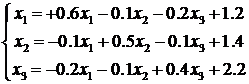
Avem ![]() deci procesul iterativ este
convergent catre solutia exacta
deci procesul iterativ este
convergent catre solutia exacta 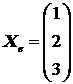 a sistemului liniar.
a sistemului liniar.
Avem relatiile de recurenta (1):
(3) 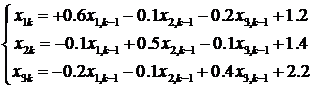
Dupa m=30 iteratii avem solutiile aproximative:
![]() ;
;
![]() ;
;
![]() .
.
Eroarea antecalculata: ![]()
Eroarea postcalculata: ![]()
Eroarea de verificare: ![]()
Programul JACOBI face aceste calcule.
b) Metoda Gauss-Seidel
Se modifica relatiile (1) astfel:
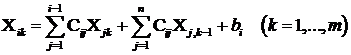
ceea ce in general mareste viteza de convergenta.
Pentru a garanta convergenta
procesului iterativ in toate cazurile, inlocuim sistemul ![]() cu sistemul
simetric
cu sistemul
simetric ![]() care are aceleasi
solutii cu
care are aceleasi
solutii cu ![]()
Exemplu
Pentru sistemul din exemplul precedent, relatiile (3) se inlocuiesc cu relatiile:
(5) 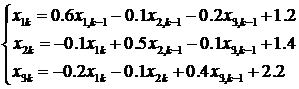
Dupa m=30 iteratii, avem solutiile aproximative:
![]() ;
;
![]() ;
;
![]()
Eroarea antecalculata este: ![]()
Eroarea postcalculata este: ![]()
Eroarea de verificare este: ![]()
Programul SEIDEL face aceste calcule.
Prin metoda Gauss-Seidel radacinile aproximative sunt mai aproape de valorile exacte si EP, EV sunt mai mici decat prin metoda Jacobi ..
c) Metoda iterativa Richardson
Fie sistemul liniar A.X = b in care A este matrice simetrica pozitiv definita .
Fie l l ln 0 valorile proprii strict pozitive ale matricii A .
Solutia X I R n va fi limita sirului recurent : X(k) = X(k - 1) + a.( b - A. X(k - 1 ) ) cu X(0) oarecare , a > 0 si k I N .
Teorema 6.1
Sirul X(k) este convergent catre solutia X a sistemului liniar A.X = b daca si numai daca
0 < a < 2 / l
Demonstratie
Fie r raza spectrala ( valoarea proprie maxima ) a matricii Richardson E - a.A .
Sirul X(k) este convergent r < 1 ali < 1 pentru orice i = 1,.,n 0 < a < 2 / li
pentru orice i = 1 ,., n .
Cum 0 < 2 / l l n rezulta 0 < a < 2 / l
Valoarea optima a lui a este a l ln) in care caz avem r l l n ) / (l l n) . Q.E.D.
Pentru k = m iteratii solutia aproximativa este X(m) , eroarea postcalculata este
EP = X(m) - X(m - 1) iar eroarea de verificare este EV = A. X(m) - b
Exemplu
Fie sistemul liniar :
3x1+ 2x2 + 2x3 = 20
2x1+ 3x2 + 2x3 = 21
2x1+ 2x2 + 3x3 = 22
Matricea sistemului liniar este :

si este simetrica , pozitiv definita avand
valorile proprii strict pozitive l l l
Luam a a l l ) = 0.25 deci sistemul recurent capata forma :
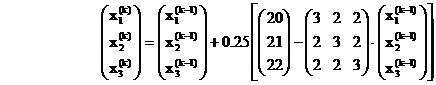 |
Vom lua ca valori initiale ale solutiilor sistemului liniar pe x1(0) = x2(0) = x3(0) = 1
Dupa k = m = 20 iteratii avem solutia aproximativa :
x1(20) = 2.012685 ; x2(20) = 3.008457 ; x3(20) = 4.004229 in timp ce solutia exacta este
x1 = 2 ; x2 = 3 ; x3 = 4
Eroarea postcalculata este EP = X(20) - X( 19) = 0.0342354 in timp ce eroarea de verificare este
EV = A. X(20) - b
Programul RICHARD face aceste calcule .
1.5 Solutii generalizate ale sistemelor liniare incompatibile
Fie un sistem liniar ![]() cu
matricea A de tip
cu
matricea A de tip ![]() , X = vector-coloana cu n
componente si b = vector-coloana cu m componente. In
plus presupunem ca
, X = vector-coloana cu n
componente si b = vector-coloana cu m componente. In
plus presupunem ca ![]() deci sistemul liniar este
incompatibil deci nu exista nici un vector-coloana X astfel ca
deci sistemul liniar este
incompatibil deci nu exista nici un vector-coloana X astfel ca ![]() .
.
Prin analogie cu solutia
clasica a sistemelor compatibile determinate ![]() , vom numi solutia
generalizata a sistemului compatibil expresia X+=A+b
unde
, vom numi solutia
generalizata a sistemului compatibil expresia X+=A+b
unde ![]() de
tip
de
tip
![]() este inversa
generalizata a matricii A, definita de relatia
este inversa
generalizata a matricii A, definita de relatia ![]() (vezi
sectiunea 1.3). In acest caz nu mai avem
(vezi
sectiunea 1.3). In acest caz nu mai avem ![]() dar
dar ![]() si b
sunt cei mai apropiati in sensul normei euclidiene dupa cum
arata:
si b
sunt cei mai apropiati in sensul normei euclidiene dupa cum
arata:
Teorema 2
Avem 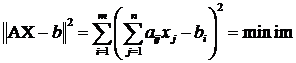 pentru
pentru ![]()
Demonstratie
Fie 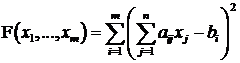 . Anulam derivatele
partiale ale lui
. Anulam derivatele
partiale ale lui ![]() in raport cu
in raport cu ![]() (conditie
necesara de minim):
(conditie
necesara de minim):
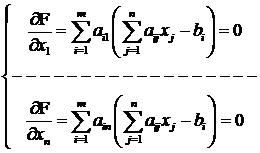
adica:
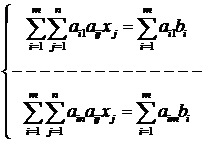
deci matricial:
(1) ![]()
Daca rang(A) = max( m, n) solutia generalizata X+ = A+b verifica conditia de minim (1).
In
adevar, pentru ![]() avem
avem ![]() deci
deci ![]() si (1)
devine:
si (1)
devine: ![]() sau:
sau: ![]() deci:
deci: ![]() .
.
Pentru ![]() avem
avem ![]() deci:
deci: ![]() si (1)
devine:
si (1)
devine: ![]() adica:
adica: ![]() . Q.E.D.
. Q.E.D.
Exemplu
Sa se afle solutia
generalizata a sistemului incompatibil cu ![]() ecuatii si
ecuatii si ![]() necunoscute:
necunoscute:
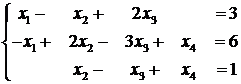
Solutie
Avem ![]() deci sistemul este
incompatibil.
deci sistemul este
incompatibil.
In sectiunea 2.3.4 am gasit: 
Solutia generalizata este 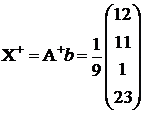 . Ea
verifica si sistemul
. Ea
verifica si sistemul ![]() .
.
Avem 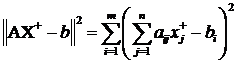
Avem:
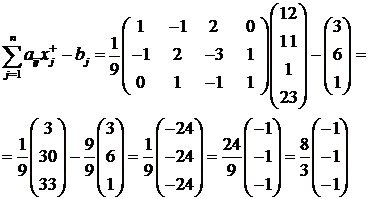
Rezulta: ![]()
2 Multimi convexe in Rn
Fie o multime de vectori U Rn . Daca ![]() , numim segmentul inchis
cu capetele X ,X multimea
, numim segmentul inchis
cu capetele X ,X multimea ![]() a vectorilor din Rn
de forma
a vectorilor din Rn
de forma ![]() cu
cu ![]() . Multimea U
se numeste convexa daca pentru orice
. Multimea U
se numeste convexa daca pentru orice ![]() avem
avem ![]() deci
odata cu vectorii
deci
odata cu vectorii ![]() multimea U contine
segmentul inchis care uneste pe
multimea U contine
segmentul inchis care uneste pe ![]() .
.
Multimea convexa U Rn este generata de vectorii ![]() daca pentru orice
daca pentru orice ![]() avem
avem ![]() cu
cu ![]() si
si ![]() .
.
Daca U1 , U2 sunt multimi convexe din Rn si α,β sunt numere reale atunci U1 ∩ U2 si
α U1 + β U2 sunt multimi convexe.
Daca A : Rn→ Rm este aplicatie liniara si U1 este multime convexa din Rn
si U2 este multime convexa din Rm atunci A (U1)= si
A -1(U2)= sunt multimi convexe .
Fie sistemul liniar ![]() unde A este matrice
dreptunghiulara cu m linii si n coloane, X IRn este vectorul-coloana al necunoscutelor iar bIRm este vectorul-coloana al termenilor liberi. In cele ce
urmeaza vom presupune conditiile restrictive:
unde A este matrice
dreptunghiulara cu m linii si n coloane, X IRn este vectorul-coloana al necunoscutelor iar bIRm este vectorul-coloana al termenilor liberi. In cele ce
urmeaza vom presupune conditiile restrictive:
1) ![]() adica numarul
ecuatiilor este strict mai mic ca numarul necunoscutelor.
adica numarul
ecuatiilor este strict mai mic ca numarul necunoscutelor.
2) rang(A) = m (ecuatiile sunt independente intre ele).
In acest caz sistemul este compatibil nedeterminat (ecuatiile sunt necontradictorii) si conform sectiunii 1.1 , solutia generala are forma:
(1) ![]()
unde xm+1,.,xn IR sunt parametri arbitrari. Aici ![]() sunt solutii liniar
independente ale sistemului
sunt solutii liniar
independente ale sistemului ![]() iar
iar 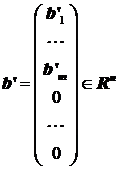 este o
solutie particulara bazica a sistemului neomogen,
obtinuta din solutia generala a sistemului neomogen pentru
este o
solutie particulara bazica a sistemului neomogen,
obtinuta din solutia generala a sistemului neomogen pentru ![]() .
.
O solutie XIRn a sistemului liniar ![]() se numeste posibila
(admisibila) daca are toate componentele nenegative:
se numeste posibila
(admisibila) daca are toate componentele nenegative: ![]() .
.
Fie U multimea
solutiilor posibile ![]() a sistemului liniar
a sistemului liniar ![]() cu
cu ![]() si
si 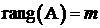 .
.
O solutie posibila ![]() se
numeste bazica daca are m componente strict pozitive
(numite bazice) restul de
se
numeste bazica daca are m componente strict pozitive
(numite bazice) restul de ![]() componente fiind nule, iar
coloanele din matricea A ce corespund celor m componente bazice strict
pozitive, formeaza o baza in Rm.
componente fiind nule, iar
coloanele din matricea A ce corespund celor m componente bazice strict
pozitive, formeaza o baza in Rm.
Exemplu
Daca in solutia (1)
de mai sus avem ![]() atunci solutia
atunci solutia ![]() este
bazica. O solutie posibila
este
bazica. O solutie posibila ![]() se numeste extremala
daca
se numeste extremala
daca ![]() cu
cu ![]() ,
, ![]() implica
implica
![]() sau
sau
![]() unde
unde
![]() .
.
Cu alte cuvinte, o solutie
posibila ![]() a sistemului liniar
a sistemului liniar ![]() cu
cu ![]() ,
, 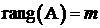 este
extremala daca ea nu este in interiorul segmentului care uneste
alte doua solutii posibile, ci la unul din capetele segmentului.
este
extremala daca ea nu este in interiorul segmentului care uneste
alte doua solutii posibile, ci la unul din capetele segmentului.
Teorema 3
Orice solutie bazica este
extremala si reciproc. Numarul acestor solutii este finit (egal
cel mult cu ![]() )
)
Demonstratie
Fie solutia bazica X. Presupunem ca X nu este solutie extremala.
Presupunand ca primele m
componente ale lui X sunt nenule, din relatia: ![]() cu
cu ![]() rezulta:
rezulta:
![]() .
Cum
.
Cum ![]() ,
,
![]() ,
rezulta de aici ca
,
rezulta de aici ca ![]() pentru
pentru 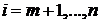 . Dar
. Dar ![]() sunt
solutii posibile asa ca avem
sunt
solutii posibile asa ca avem ![]() . Cum
. Cum ![]() sunt
vectori-coloana liniar independenti (X = solutie bazica)
rezulta
sunt
vectori-coloana liniar independenti (X = solutie bazica)
rezulta ![]() si pentru
si pentru ![]() asa ca
asa ca ![]() absurd. Rezulta
ca X este solutie extremala.
absurd. Rezulta
ca X este solutie extremala.
Reciproc, fie
X=solutie extremala cu ![]() pentru
pentru ![]() .
.
Sa aratam ca X
este solutie bazica adica vectorii-coloana ![]() sunt
liniar independenti. Daca
sunt
liniar independenti. Daca ![]() n-ar fi liniar
independenti, am avea
n-ar fi liniar
independenti, am avea ![]() cu
cu ![]() nu toti nuli.
Dar
nu toti nuli.
Dar ![]() deci
rezulta egalitatile:
deci
rezulta egalitatile:
![]()
![]()
![]() poate fi ales suficient de
mic astfel ca:
poate fi ales suficient de
mic astfel ca: ![]() ;
; ![]() pentru
pentru ![]() .
.
Rezulta ca:
![]()
![]()
sunt solutii posibile si in plus: ![]() ceea ce
contrazice faptul ca X este solutie extremala. Rezulta
ca X este solutie bazica. Avem
ceea ce
contrazice faptul ca X este solutie extremala. Rezulta
ca X este solutie bazica. Avem ![]() grupuri de m
componente nenule din n componente posibile deci avem
grupuri de m
componente nenule din n componente posibile deci avem ![]() solutii
extremale s bazice. Q.E.D.
solutii
extremale s bazice. Q.E.D.
Teorema 4
Daca sistemul de ecuatii liniare ![]() ,
, ![]() are
solutii posibile, are si solutii posibile bazice.
are
solutii posibile, are si solutii posibile bazice.
Demonstratie
Fie X o solutie posibila a sistemului din enunt cu primele m componente nenule.
Sa aratam ca
vectorii-coloana ![]() sunt liniar
independenti.
sunt liniar
independenti.
Daca ![]() n-ar fi liniar
independenti am avea
n-ar fi liniar
independenti am avea ![]() cu
cu ![]() nu toti nuli.
Daca notam
nu toti nuli.
Daca notam ![]() avem
avem ![]() deci
deci ![]() pentru
orice l
real.
pentru
orice l
real.
Sa determinam pe l astfel ca ![]() . Fie
. Fie ![]() si
si ![]() si
fie:
si
fie:
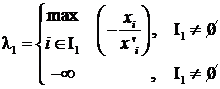 ;
; 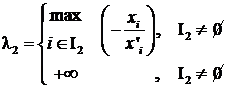
Este clar ca pentru l cu ![]() avem
avem ![]() . Putem
alege un
. Putem
alege un ![]() astfel ca solutia
posibila
astfel ca solutia
posibila ![]() sa aiba cel mult m-1
componente nenule: daca
sa aiba cel mult m-1
componente nenule: daca ![]() luam
luam ![]() iar
daca
iar
daca ![]() luam
luam ![]() .
Daca coloanele corespunzatoare componentelor nenule ale solutiei
.
Daca coloanele corespunzatoare componentelor nenule ale solutiei
![]() (in
numar de cel mult m-1) sunt liniar independente, aceasta ar fi
solutie bazica.
(in
numar de cel mult m-1) sunt liniar independente, aceasta ar fi
solutie bazica.
In caz contrar se reia rationamentul aplicat mai sus, obtinandu-se o noua solutie cu cel mult m-2 componente nenule, etc., deci dupa un numar finit de pasi am ajunge la solutia nula (cu zero componente nenule) care este evident solutie bazica. Q.E.D.
Teorema 5
Multimea solutiilor
posibile U Rn ale sistemului liniar ![]() ,
, ![]() este o
multime convexa generata de solutiile bazice in numar
finit.
este o
multime convexa generata de solutiile bazice in numar
finit.
Demonstratie
Fie ![]() deci
deci ![]() ,
, ![]() si
si ![]() .
.
Pentru orice ![]() avem
avem ![]() si in plus
si in plus ![]() deci U
este multime convexa.
deci U
este multime convexa.
Fie ![]() astfel ca pentru orice
astfel ca pentru orice ![]() avem:
avem: ![]()
Presupunem ca p este
minim in raport cu aceste proprietati. Sa aratam
ca ![]() sunt
solutii extremale (deci conform teoremei 3 si bazice). Daca de
exemplu
sunt
solutii extremale (deci conform teoremei 3 si bazice). Daca de
exemplu ![]() n-ar
fi solutie extremala am avea:
n-ar
fi solutie extremala am avea: ![]() unde
unde
![]() si
si ![]() . Dar
. Dar ![]() si
si ![]() .
Rezulta:
.
Rezulta:
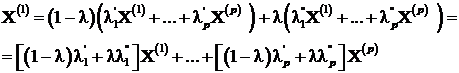
Daca ![]() am avea:
am avea:
![]() cu
cu ![]() si
si ![]() contrar
minimalitatii lui p.
contrar
minimalitatii lui p.
La aceeasi concluzie am ajunge daca:
![]() caci
am avea:
caci
am avea:
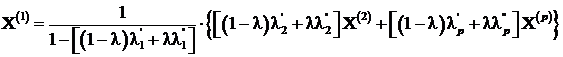
Rezulta ca ![]() deci cum:
deci cum: ![]()
cu ![]() avem:
avem: ![]() pentru
pentru ![]() si
cum
si
cum ![]() rezulta
rezulta
![]() pentru
pentru
![]() .
Insa
.
Insa ![]() ;
; ![]() asa ca
rezulta
asa ca
rezulta ![]() deci am avea
deci am avea ![]() absurd. Q.E.D.
absurd. Q.E.D.
Exemplu
Se da sistemul liniar: 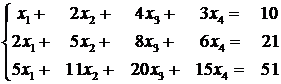
Sa se afle solutia generala X 0 a sistemului liniar ca o combinatie liniara convexa a solutiilor posibile bazice.
Solutie
|
Baza |
A1 |
A2 |
A3 |
A4 |
B |
|
E1 |
2 |
4 |
3 |
10 |
|
|
E2 |
2 |
5 |
8 |
6 |
21 |
|
E3 |
5 |
11 |
20 |
15 |
51 |
|
A1 |
1 |
2 |
4 |
3 |
10 |
|
E2 |
0 |
0 |
0 |
1 |
|
|
E3 |
0 |
1 |
0 |
0 |
1 |
|
A1 |
1 |
0 |
4 |
3 |
10 |
|
A2 |
0 |
1 |
0 |
0 |
1 |
|
E3 |
0 |
0 |
0 |
0 |
0 |
Avem ![]() deci sistemul este
compatibil nedeterminat. Ecuatia secundara numarul 3 se elimina
din sistem fiind liniar dependenta de primele doua.
deci sistemul este
compatibil nedeterminat. Ecuatia secundara numarul 3 se elimina
din sistem fiind liniar dependenta de primele doua.
Sistemul capata forma: 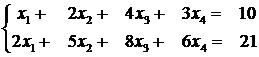 .
Solutiile posibile bazice
.
Solutiile posibile bazice 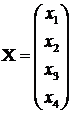 au 2 componente strict
pozitive (bazice) si 2 componente nule (nebazice).
au 2 componente strict
pozitive (bazice) si 2 componente nule (nebazice).
CAZURI:
1) ![]() . Rezulta
. Rezulta 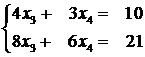 care
este sistem incompatibil
care
este sistem incompatibil
2) ![]() . Rezulta
. Rezulta 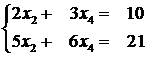 de unde
de unde 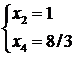
Avem prima solutie
posibila bazica 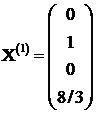
3) ![]() . Rezulta
. Rezulta 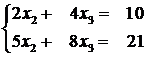 de unde
de unde 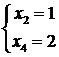
Avem a doua solutie
posibila bazica 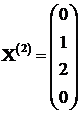
4) ![]() . Rezulta
. Rezulta 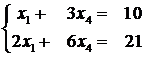 care
este sistem incompatibil.
care
este sistem incompatibil.
5) ![]() . Rezulta
. Rezulta 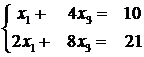 care
este sistem incompatibil.
care
este sistem incompatibil.
6) ![]() . Rezulta
. Rezulta  de unde
de unde 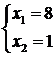
Rezulta a treia solutie
posibila bazica: 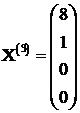 . Conform teoremei 5 ,orice
alta solutie posibila
. Conform teoremei 5 ,orice
alta solutie posibila 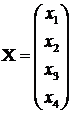 cu
cu ![]() este
combinatia liniara convexa a solutiilor posibile bazice:
este
combinatia liniara convexa a solutiilor posibile bazice: 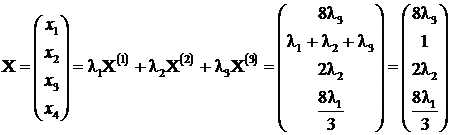 unde
unde ![]() si
si ![]() .
.
Programul SOLBAZ calculeaza toate solutiile bazice si calculeaza valorile unei functii liniare / patratice f pe multimea acestor solutii bazice , gasind valoarea maxima si minima a lui f (vezi sfarsitul sectiunii 3) .
3 Extremele unui polinom convex concav pe o multime convexa in Rn
Fie U Rn o multime convexa.
O functie f: U R
este convexa daca pentru orice ![]() si orice
si orice ![]() avem:
avem:
![]()
O functie f: U R
este concava daca pentru orice ![]() si orice
si orice ![]() avem:
avem:
![]()
Daca f, g sunt
functii convexe / concave pe U si ![]() atunci functia
atunci functia ![]() este
convexa / concava pe U.
este
convexa / concava pe U.
Exemplu
Functia polinomiala
liniara ![]() este si convexa
si concava pe Rn .
este si convexa
si concava pe Rn .
Teorema 6
Functia f: U Rn R este convexa daca si numai
daca pentru ![]() avem:
avem:
![]()
adica hiperplanul tangent la graficul lui
f in ![]() ramane sub graficul lui
f.
ramane sub graficul lui
f.
Demonstratie
Daca f este functie convexa, din relatia (1) rezulta:
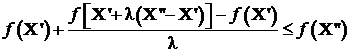
Trecem la limita pentru ![]() ,
, ![]() si
tinem cont ca:
si
tinem cont ca:
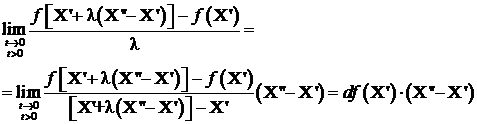
asa ca: ![]() deci relatia (3).
deci relatia (3).
Reciproc, fie
relatia (3) indeplinita: ![]() .
.
Schimband pe ![]() cu
cu ![]() avem:
avem:
![]()
In relatia (3) inlocuim pe ![]() cu X
si inmultim relatia obtinuta cu l
cu X
si inmultim relatia obtinuta cu l
![]()
In relatia (4) inlocuim pe ![]() si
inmultim relatia obtinuta cu
si
inmultim relatia obtinuta cu ![]() :
:
(6) ![]()
Adunand relatiile (5)
si (6) obtinem: ![]() deci f este
convexa pe U. Q.E.D.
deci f este
convexa pe U. Q.E.D.
Pentru functia f: U Rn R , aceasta este concava daca
si numai daca pentru orice ![]() avem:
avem:
![]()
adica hiperplanul tangent la graficul lui
f in ![]() ramane deasupra
graficului lui f.
ramane deasupra
graficului lui f.
Conform formulei Taylor avem:
![]()
Pentru ![]() suficient de aproape de
suficient de aproape de ![]() ,
relatia (3) capata forma:
,
relatia (3) capata forma:
![]() pentru
orice
pentru
orice ![]() .
.
deci f este convexa pe U Rn daca si numai daca este indeplinita relatia (8).
In mod analog relatia (7) capata forma:
![]() pentru
orice
pentru
orice ![]() .
.
Deci f este concava pe U Rn daca si numai daca este indeplinita relatia (9).
Exemplu
Fie functia polinomiala
patratica: ![]() unde D este matrice
simetrica de ordin n, C este vector-coloana cu n
componente iar eIR
unde D este matrice
simetrica de ordin n, C este vector-coloana cu n
componente iar eIR
Conditia (8) revine la
![]() pentru
orice
pentru
orice 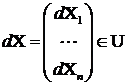 deci
f este convexa daca si numai daca matricea D este
pozitiv definita.
deci
f este convexa daca si numai daca matricea D este
pozitiv definita.
Conditia (9) revine la
![]() pentru
orice
pentru
orice 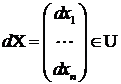 deci
f este concava daca si numai daca matricea D este
negativ definita.
deci
f este concava daca si numai daca matricea D este
negativ definita.
Un criteriu pentru matrici simetrice D pozitiv definite, respectiv negativ definite este dat de Sylvester si a fost demonstrat in sectiunea 4.3.2 (teorema 4.8):
Fie 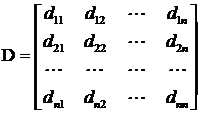 cu
cu ![]() matricea
simetrica a partii
matricea
simetrica a partii ![]() din functia polinomiala
patratica:
din functia polinomiala
patratica:![]()
Fie minorii principali:
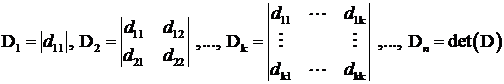
Matricea D este pozitiv definita
daca si numai daca ![]() .
.
Matricea D este negativ definita
daca si numai daca ![]()
Functiile polinomiale patratice
convexe (cu matricile D pozitiv definita) au un minim unic dat de
relatiile: ![]() deci punctul de minim este
vectorul din Rn :
deci punctul de minim este
vectorul din Rn :
![]()
Functiile polinomiale patratice concave
(cu matricea D negativ definita) au un maxim unic ![]() , dat de
relatia (10).
, dat de
relatia (10).
Valoarea minimului / maximului este ![]() .
.
Exemple
1) Se da functia polinomiala patratica:
![]()
Sa se arate ca functia f
este convexa pe R3 si sa se gaseasca
punctul de minim ![]() si valoarea minimului
si valoarea minimului ![]() .
.
Solutie
Avem 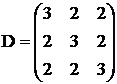 ;
;  ;
; ![]()
Avem ![]() ;
; 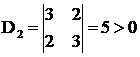 ;
; ![]() deci f
este functie convexa pe R3. Punctul de minim
deci f
este functie convexa pe R3. Punctul de minim ![]() este:
este: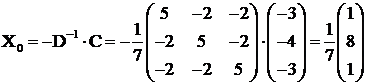 deci
deci ![]() ;
; ![]() ;
; ![]()
Valoarea minimului este: 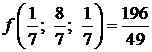
2) Se da functia:
![]()
Sa se arate ca functia este
concava pe R3 si sa se gaseasca
punctul de maxim ![]() si valoarea maximului
si valoarea maximului ![]() .
.
Solutie
Avem: 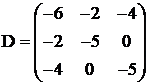 ;
; 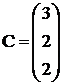 ;
; ![]()
Avem ![]() ;
; 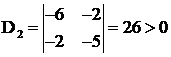 ;
; ![]() deci f
este functie concava pe R3. Punctul de maxim
deci f
este functie concava pe R3. Punctul de maxim ![]() este:
este:
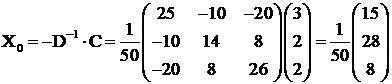 deci
deci ![]() ;
; ![]() ;
; ![]() . Valoarea
maximului este:
. Valoarea
maximului este: 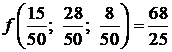
Functia liniara ![]() nu are
nici minim nici maxim desi este si convexa si concava.
nu are
nici minim nici maxim desi este si convexa si concava.
O solutie posibila X(0)
IRn, X(0) 0 a sistemului liniar ![]() cu
cu ![]() si
si 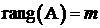 se
numeste solutie optima daca valoarea
se
numeste solutie optima daca valoarea ![]() este
maxima sau minima. In continuare ecuatiile sistemului liniar
este
maxima sau minima. In continuare ecuatiile sistemului liniar ![]() , le vom
numi legaturi sau restrictii.
, le vom
numi legaturi sau restrictii.
Teorema 7
Daca o functie liniara ![]() cu
legaturi liniare
cu
legaturi liniare ![]() ,
, ![]() are solutii
optime, are si solutii bazice optime.
are solutii
optime, are si solutii bazice optime.
Demonstratie
Fie X o solutie optima (de exemplu
cu ![]() )
cu primele m componente nenule. Sa aratam ca
vectorii-coloana
)
cu primele m componente nenule. Sa aratam ca
vectorii-coloana ![]() sunt liniar
independenti. Daca
sunt liniar
independenti. Daca ![]() n-ar fi liniar
independenti, ca si in demonstratia teoremei 4 am gasi
solutia posibila
n-ar fi liniar
independenti, ca si in demonstratia teoremei 4 am gasi
solutia posibila ![]() . Daca X este
solutie optima (presupusa de minim pentru f) deci:
. Daca X este
solutie optima (presupusa de minim pentru f) deci: ![]() asa
ca
asa
ca ![]() .
Nu putem avea
.
Nu putem avea ![]() deoarece alegand l de semn contrar lui
deoarece alegand l de semn contrar lui ![]() am avea
am avea ![]() absurd
caci
absurd
caci ![]() . Rezulta
. Rezulta ![]() asa
ca
asa
ca ![]() este
deasemenea solutie optima.
este
deasemenea solutie optima.
Ca si in demonstratia
teoremei 4, solutia optima ![]() poate avea cel mult m-1
componente nenule deci dupa un numar finit de pasi ajungem la o
solutie bazica optima. Q.E.D.
poate avea cel mult m-1
componente nenule deci dupa un numar finit de pasi ajungem la o
solutie bazica optima. Q.E.D.
Teorema 8
Multimea solutiilor optime ![]() ale unei
functii liniare
ale unei
functii liniare ![]() cu legaturi liniare
cu legaturi liniare ![]() ,
, ![]() , este o
multime convexa generata de solutiile bazice optime in
numar finit.
, este o
multime convexa generata de solutiile bazice optime in
numar finit.
Demonstratie
Fie ![]() cu
cu ![]() ,
, ![]() ;
; ![]() ;
; ![]()
Pentru orice ![]() ,
, ![]() este solutie
posibila, conform teoremei 5
este solutie
posibila, conform teoremei 5
Mai mult,
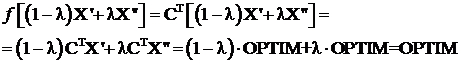
deci V este multime convexa. A doua parte a enuntului se demonstreaza analog cu a doua parte a enuntului teoremei In particular daca V se reduce la o solutie optima, aceasta este bazica. Q.E.D.
Schema relatiilor intre
multimea solutiilor posibile U, multimea solutiilor optime
V, multimea solutiilor bazice ![]() si multimea
solutiilor optime bazice
si multimea
solutiilor optime bazice ![]() , este urmatoarea:
, este urmatoarea:
|
Solutii posibile |
U | |||
|
Solutii bazice | ||||
|
Solutii Optime |
Solutii bazice optime VB |
V |
||
|
UB | ||||
Exemplu
In sectiunea 2 s-a rezolvat
sistemul liniar: 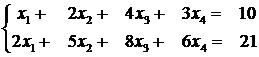
(a treia ecuatie s-a inlaturat, fiind liniar dependenta de primele doua) si s-au gasit trei solutii bazice:
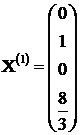 ;
; 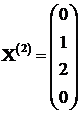 ;
; 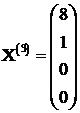
Multimea convexa U ale
solutiilor posibile ![]() ale sistemului liniar
precedent este
ale sistemului liniar
precedent este ![]()
Daca multimea
convexa U este marginita (este complet
continuta intr-o sfera de raza infinita) si
inchisa (isi contine frontiera) atunci orice functie
liniara ![]() are solutie optima
pe U, care daca este unica este neaparat bazica conform
teoremei 8
are solutie optima
pe U, care daca este unica este neaparat bazica conform
teoremei 8
De exemplu functia ![]() are
valorile
are
valorile 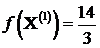 ;
; ![]() ;
; ![]() deci
deci ![]() pentru
pentru ![]() si
si ![]() pentru
pentru ![]() .
.
Rezumat
In continuare se studiaza convexitatea multimii solutiilor unui sistem liniar compatibil nedeterminat cu evidentierea solutiilor bazice(extremale)
In final se prezinta extremele unui polinom convex/concav pe multimea convexa a solutiilor sistemului linia compatibil nedeterminat ca o pregatire pentru programarea liniara din cap.6
Intrebari
Ce forma are solutia generala a unui sistem de ecuatii liniare ?
Cum se reduc operatiile cu polinoame la sisteme de ecuatii liniare ?
3. Ce forma are solutia generala a unui sistem de ecuatii liniare ca o combinatie liniara convexa de solutii bazice ?
4. Cum se recunoaste daca un polinom de grad 2 este convex /concav si unde se ating extremele sale pe multimea convexa a solutiilor unui sistem liniar compatibil nedeterminat ?
6 Bibliografie
Stanasila O. " Analiza liniara si geometrie "Vol. I - II,Editura ALL ,2000 - 2001
Cenusa Gh. si col." Matematici pentru economisti " Editura CISON,2000
Cenusa Gh. si col." Matematici pentru economisti - culegerede probleme" Editura CISON,2000
4. Ene D. " Matematici (I) " Editura CERES , 2004
Gogonea S. , Ene D. " Analiza numerica " Editura Cartea Universitara , 2005
6. Ene D. , Gogonea S. " Metode numerice" Editura Cartea universitara , 2005
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2294
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved