| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
2. Reducerea sistemelor de forte concurente
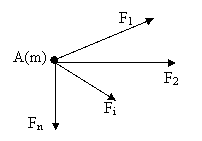 Se
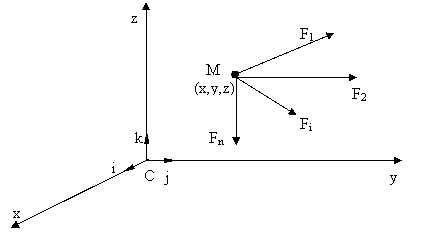
considera un punct material de masa m
actionat de fortele F1 . F n (fig. 2.1). Fortele care
actioneaza asupra unui punct material de masa m sunt forte concurente.
Se
considera un punct material de masa m
actionat de fortele F1 . F n (fig. 2.1). Fortele care
actioneaza asupra unui punct material de masa m sunt forte concurente.
Forta este un vector legat .
Problema care se pune este de a reduce acest sistem
de forte .
- poligonului
b) analitica
a) Metoda grafica (fig. 2.2)
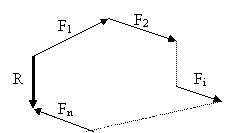
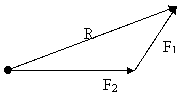
 reg. paralelogramului reg. triunghiului reg. poligonului
reg. paralelogramului reg. triunghiului reg. poligonului
R=F1+F2
![]()
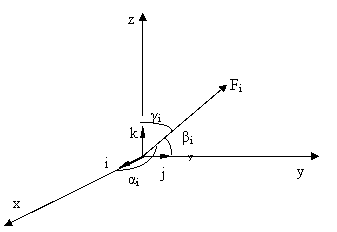
Fig. 2.2
b) Metoda analitica (fig. 2.3)
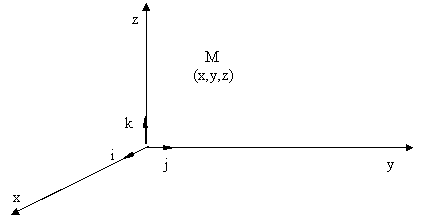
Se considera un triedru de referinta triortogonal
drept xOyz si punctul material de masa m situat
in centrul O actionat de fortele concurente Fi .
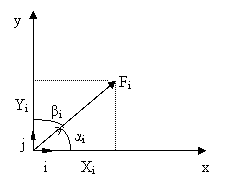
Fi face cu axele x , y , z unghiurile ai , bi , gi .
Fig. 2.3
Tipuri de probleme :
b1) Date : Fi ai , b i, gi
Se cer : Xi, Yi, Zi
Xi = Fi cosai
Yi = Fi cosbi cos2ai + cos2 bi + cos2 gi = 1
Zi = Fi cosgi
b2) Date : Xi ,Yi , Zi
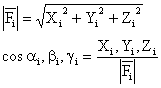
Se cer : Fi ai , b i,
gi
 b3)
Caz particular : Forte in plan
b3)
Caz particular : Forte in plan
(fig. 2.4)
Date : Fi ai , b i, =ai - π/2

Se cer : Xi ,Yi
Fig. 2.4

2.1. Teorema proiectiilor
Se considera un sistem de forte concurente F1 .F2 care actioneaza asupra unui punct material .
![]()
Descompunand fortele pe cele trei directii x , y , z putem scrie :
![]()
.
![]()
![]() (4)
(4)
Facand suma relatiilor Þ
![]() (5)
(5)
Notam : ![]() - vector rezultant ( rezultanta ) (6)
- vector rezultant ( rezultanta ) (6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Teorema proiectiilor: Proiectia vectorului rezultant pe o axa D este egala cu suma proiectiilor vectorilor componenti pe acea axa .
![]() (11)
(11)
Observatie Proiectia unui vector pe o axa este un scalar, proiectia unui vector pe un plan este un vector .
Concluzie : Un sistem de forte concurente care actioneaza asupra unui punct material este echivalent cu o forta unica rezultanta R .
![]() - modul (12)
- modul (12)
Caz particular : forte in plan :
![]() - modul (14)
- modul (14)
si ![]() - directie (15)
- directie (15)
|
Metoda grafica |
Metoda analitica |
Sistem echivalent cu |
Observatii |
|
|
R ¹ 0 |
poligonul fortelor nu s nu se inchide |
cel putin una din proiectii ¹ 0 SXi , SYi , SZi ¹ |
o forta unica "Rezultanta" |
A(m) capata o miscare cu a R = ma |
|
R = 0 |
poligonul fortelor se inchide |
SXi2+SYi2+SZi2= X = Y = Z = 0 |
sistem echivalent cu "zero" |
A(m) a) t = 0 ; v = 0 repaus b) t = 0 ; v ¹ 0 v = vo miscare rectilinie uniforma |
Sa se determine rezultanta sistemului de forte reprezentate in fig. 2.5. Fortele F2 si F3 sunt continute in planul xOy , F1 este continuta in planul yOz , iar forta F4 in planul xOz.
|
|
3. Echilibrul punctului material
3.1. Echilibrul punctului material liber
Punctul material liber este punctul care poate sa ocupe orice pozitie in spatiu (nu are nici o obligatie geometrica).
Pozitia sa la un moment dat este definita prin coordonatele scalare x, y, z, adica prin 3 parametrii independenti, se spune ca punctul material liber are 3 grade de libertate.
 Fie
un punct material liber oarecare M, a carui pozitie este raportata la un sistem
de referinta convenabil ales si sistemul de forte concurente Fi (
i = 1 , 2 . n ) care actioneaza asupra punctului considerat ,
(fig. 3.1).
Fie
un punct material liber oarecare M, a carui pozitie este raportata la un sistem
de referinta convenabil ales si sistemul de forte concurente Fi (
i = 1 , 2 . n ) care actioneaza asupra punctului considerat ,
(fig. 3.1).
Fig. 3.1
Conditia necesara si suficienta ca punctul material liber sa fie in echilibru este ca sistemul de forte sa fie echivalent cu zero .
![]()
Deci conditia necesara si suficienta de
echilibru se poate scrie:
Rezultanta R a fortelor care actioneaza asupra punctului material proiectata pe axe:
![]()
Relatiile (1) si (2) scrise scalar devin:

Probleme posibile :
se dau fortele ; se cere pozitia de echilibru.
se da pozitia de echilibru ; se cer fortele.
se dau partial fortele si partial pozitia de echilibru ; se cer complet fortele care actioneaza asupra punctului material si complet pozitia de echilibru.
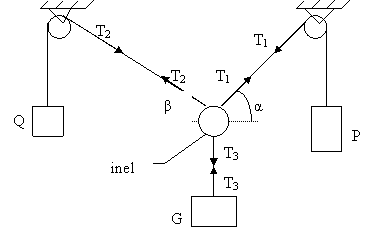 Aplicatia
1 :
Aplicatia
1 :
Date : |G| , |P| , |Q| (fig. 3.2)
Se cer : pozitia de echilibru a si b = ?
Obs: Firele sunt considerate complet flexibile si inextensibile.
(pot fi supuse numai la tensiuni)
Fig. 3.2
Conditia de echilibru vectorial :
![]() (4)
(4)
![]() (5)
(5)
|
|
Alegem un sistem de referinta convenabil xOy .
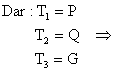
Relatia (4) proiectata pe axele de coordonate devine
(fig. 3.3) :

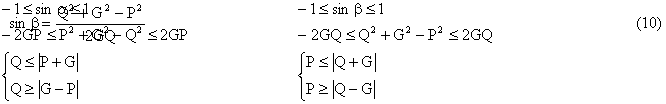
Obs .Probleme de statica in care numarul necunoscutelor scalare depaseste numarul ecuatiilor de echilibru si care nu ofera alte relatii suplimentare independente intre aceste necunoscute se numesc probleme static nedeterminate .
3.2. Echilibrul punctului material cu legaturi
Legatura in mecanica este o obligatie geometrica (obligativitatea punctului material de a ramane pe o suprafata, pe o curba sau intr-un punct fix) .
O legatura poate fi inlocuita cu o forta denumita forta de legatura sau reactiune .
|
|
Un punct material aflat pe o suprafata are 2 grade de libertate (fig. 3.4)
Un punct material aflat pe o curba are un grad de libertate (fig. 3.5)
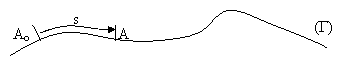
 Un
punct material fixat in spatiu nu are nici un grad de libertate (fig. 3.6)
Un
punct material fixat in spatiu nu are nici un grad de libertate (fig. 3.6)
Fig. 3.6
forta de legatura = reactiune (N)
3.2.1. Echilibrul punctului material cu legaturi ideale (fara frecare)
Se numesc legaturi ideale acele legaturi care nu comporta frecari .
![]()
Conditia de echilibru - sistemul de forte alcatuit din fortele efectiv aplicate
si fortele de legatura sa fie echivalent cu zero .
Σ Fi - fortele efectiv aplicate
N - rezultanta fortelor de legatura
Sub actiunea fortelor efectiv aplicate si a fortelor de legatura, punctul material poate fi considerat punct material liber si echilibrul se poate studia ca la punctul 3. 1.
Legaturi : 1) bilaterale - legatura pe care punctul material nu o poate parasi in nici un sens (fig. 3.7)
2) unilaterale - legatura pe care o poate parasi (fig. 3.8)
1)
|
|
cursor bara tor
Fig. 3.7

 2)
2)
interior cilindru sfera fir fir
Fig. 3.8
Solutiile care sunt posibile pentru legaturi bilaterale nu sunt posibile pentru legaturi unilaterale .
Aplicatia 2
Date : G , a, (fig. 3.9)
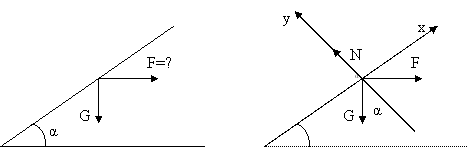 Se
cere : F = ? pentru echilibru
Se
cere : F = ? pentru echilibru
Conditia de echilibru :
G + F + N = 0 (11)
Fig. 3.9

Descompusa pe axe relatia (11) devine:

3.2.2. Echilibrul punctului material cu legaturi cu frecare
La considerarea fortelor de legatura ale punctului material rezemat pe o suprafata sau o curba, trebuie sa tinem seama si de componenta tangentiala (T) a acestora denumita forta de frecare de alunecare, care se opune miscarii sau tendintei de miscare a punctului material .
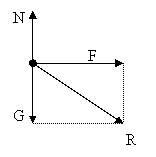
Se considera o suprafata rugoasa pe care se afla un corp de greutate G tras cu o forta orizontala F
(fig. 3.10) .
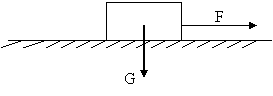
Fig. 3.10
Se asimileaza corpul cu un punct material si se izoleaza prin introducerea reactiunii normale la plan.
 Conditia
vectoriala de echilibru este :
Conditia
vectoriala de echilibru este :
G+F+N = 0 (15)
Prin proiectare pe axe relatia (15) devine: (fig. 3.11) Þ
G + N = 0 F = 0 (16)
Fig. 3.11
Experimental se constata ca miscarea nu are loc chiar pentru F ¹ 0 . Aceasta a dus la concluzia ca exista o forta T care se opune miscarii numita forta de frecare la alunecare .
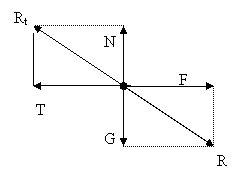 Deci
conditia corecta de echilibru este (fig. 3.12) :
Deci
conditia corecta de echilibru este (fig. 3.12) :
G+F+N+T = 0 (17)
R Rt
forte efectiv aplicate forte de legatura
Fig. 3.12
3.2.2.1. Frecarea de alunecare. Legile frecarii ( Coulomb 1779 )
Valoarea maxima a fortei de frecare de alunecare nu depinde de viteza relativa a corpului si de marimea suprafetei de contact cu planul.
Forta de frecare de alunecare maxima este proportionala cu reactiunea normala N .
|Tmax|=μ|N| m - coeficient de frecare adimensional (18)
Proprietatile lui T :
directia ei este tangenta la suprafata sau curba de reazem a punctului material
sensul ei este invers tendintei de alunecare a punctului material
echilibrul se realizeaza pentru valori ale fortei de frecare T £ m N -conditia de echilibru.
Conditia de echilibru pentru un punct material supus la legaturi cu frecare :

|
|
Se noteaza cu α unghiul dintre N si Rt (fig. 3.13)
![]()
La limita T = Tmax si notand αmax = φ =>

Echilibrul se realizeaza pentru T ≤ Tmax │: N Fig. 3.13
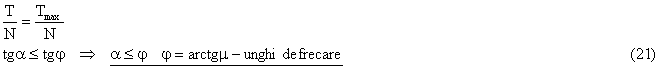
Conditia a £ j rezida in faptul ca rezultanta fortelor exterioare R = G + F sa faca cu normala in punctul de contact un unghi mai mic decat unghiul de frecare .
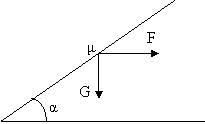 Aplicatia
3
Aplicatia
3 Date : G , a , m (fig. 3.14)
Se cere : F = ? pentru echilibru
Conditia de echilibru :
G + F + N + T =0 (22) Fig. 3.14
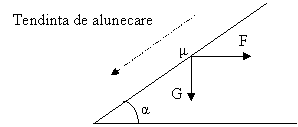
Fig. 3.15
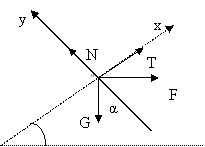

Proiectata pe axe relatia (22) devine (fig. 3.16) :

Cazul 2 (fig. 3.17)
Conditia de echilibru :
G+F+N + T =0 (27)
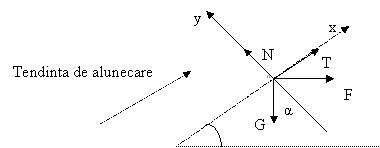
Fig. 3.17

Proiectata pe axe relatia (27) devine:


|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1703
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved