| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Siruri si serii de functii
A)Dictionar
Interpretarea
geometrica la marginirea uniforma pentru (fn)n![]() 1 pe D
1 pe D![]() ,cu
D=[a,b]
,cu
D=[a,b]
Graficul functiilor fn,n![]()
sunt continute in banda orizontala cuprinsa intre
dreptele de ecuatii x = -M si y = M
Observatie :Este imediat(a se vedea interpretarile
geometrice corespunzatoare) ca un sistem de functii uniform convergent pe D![]() este uniform marginit pe D
este uniform marginit pe D
fn :D->![]() ,
,![]() n
n![]() 1 (D
1 (D![]()
![]() )(sau,echivalent,
serie de functii definita de sirul de functii (fn)n
)(sau,echivalent,
serie de functii definita de sirul de functii (fn)n![]() 1) : perechea ((fn)n,(sn)n),
unde :
1) : perechea ((fn)n,(sn)n),
unde :
s1=f1;
s2=f1+f2;;sn=f1+fn;![]() n
n![]() 1
1
(sn:D->![]() ,
,![]() n
n![]() 1)
1)
Se noteaza ![]() sau
sau ![]() sau f1+f2+fn+
si uneori pentru ca marea diferenta de o serie numerica se scrie
sau f1+f2+fn+
si uneori pentru ca marea diferenta de o serie numerica se scrie ![]() (x),x
(x),x![]() D.
D.
Termenii
seriei ![]() : functiile f1,f2,,fn,
: functiile f1,f2,,fn,
Sirul
sumelor partiale ale seriei de functii ![]() (cu ((fn)n
(cu ((fn)n![]() 1)
1)![]() F(D,
F(D,![]() )) :
)) :
o serie de
functii ![]() ,cu
,cu ![]()
![]() F(D,
F(D,![]() ) cu sn=f1+f2++fn
,
) cu sn=f1+f2++fn
,![]() n
n![]() 1 (sn
=suma partiala de ordinul n a seriei
1 (sn
=suma partiala de ordinul n a seriei ![]() )
)
Serie de functii simlu convergenta(sau partial convergenta) pe D
o serie de
functii ![]() ,cu(
,cu(![]()
![]() F(D,
F(D,![]() ),a.i. sirul absciat de functii
),a.i. sirul absciat de functii ![]()
![]() F(D,
F(D,![]() ) al sumelor partiale de ordin n cu n
) al sumelor partiale de ordin n cu n![]() 1,este simplu(punctual)convergent pe D, deci
1,este simplu(punctual)convergent pe D, deci ![]() s
s ![]() F(D,
F(D,![]() ) a.i. sn
) a.i. sn![]() S
S
Functia S :D![]()
![]() de mai sus e numita suma punctuala a seriei
de mai sus e numita suma punctuala a seriei ![]() ,pe D.Se noteaza :
,pe D.Se noteaza :

S(x)=![]() (x),x
(x),x![]() D
D
Serie de functii
uniform convergenta pe D :
o serie de functii ![]() ,cu
,cu ![]()
![]() F(D,
F(D,![]() ) a.i. sirul
asociat de functii
) a.i. sirul
asociat de functii ![]()
![]() F(D
F(D![]() ),al sumelor
partiale de ordin n cu n
),al sumelor
partiale de ordin n cu n![]() 1,este uniform convergenta pe D, deci
1,este uniform convergenta pe D, deci ![]() S
S![]() F(D,
F(D,![]() ) a.i. Sn
) a.i. Sn![]() S
S
 Fuctia S:D
Fuctia S:D![]()
![]() de mai sus
este numita suma uniforma a seriei
de mai sus
este numita suma uniforma a seriei ![]() ,pe D.
,pe D.
Se noteaza S= ![]() pe D
pe D
Serie de
functii absolut convergenta in punctul x0![]() D :
D :
o serie de
functii ![]() cu
cu ![]()
![]() F(D,
F(D,![]() ) a.i. seria numerica
) a.i. seria numerica ![]() este convergenta.Serie numerica
este convergenta.Serie numerica ![]() este n
este n![]() 1 serie de
termeni pozitivi.
1 serie de
termeni pozitivi.
Serie de functiiabsolut convergenta pe D :
o serie de
functii ![]() cu
cu ![]()
![]() F(D,
F(D,![]() ) astfel incat
) astfel incat ![]() este absolut
convergenta in x0
este absolut
convergenta in x0![]() D.
D.
Observatie
1. O serie de
functii ![]() absolut convergenta in
x0
absolut convergenta in
x0![]() D,este convergenta in x0
D,este convergenta in x0![]() D (adica seria numerica
D (adica seria numerica ![]() x0 este convergenta).
x0 este convergenta). ![]() x0 este si o serie numerica.
x0 este si o serie numerica.
2. O serie de functii absolut convergenta pe D este simplu convergenta pe D
Restul de
ordin n al unei serii convergente de functii ![]() (serii punctual convergente&serii uniform convergente)
(serii punctual convergente&serii uniform convergente)
seria![]() =fn+1+fn+2+
=fn+1+fn+2+
![]()
![]() (
(![]() =(f1+f2++fn)+(fn+1+fn+2+))
=(f1+f2++fn)+(fn+1+fn+2+))
Sn restul de ordin 22
Multimea de
convergenta a seriei de functii ![]() ,fn :D
,fn :D![]()
![]() ,n
,n![]() 1 :
1 :
cea mai mare
submultime Dc![]() D pe care seria este convergenta.
D pe care seria este convergenta.
Deci Dc=![]()
![]()
Exelplu 1 [Sir de functii care este simplu convergent pe multimea D de definitie, fara a fi convergent]
![]()
![]() , fn :[0,1]
, fn :[0,1]![]()
![]() ,fn
,fn![]() xn ,
xn ,![]() n
n![]() 1 ; xn,n
1 ; xn,n![]() 1 ;x
1 ;x![]() [0,1] f
[0,1] f
![]()
![]()
![]()
![]()
![]()
![]()
![]() fn
fn![]() f si fn
f si fn![]() f ,unde f :[0,1]
f ,unde f :[0,1]![]()
![]() este functie f(x)=
este functie f(x)= ![]()
0 1 x
![]() Intr-adevar ,fie
Intr-adevar ,fie ![]() >0.Trebuie gasit pentru
>0.Trebuie gasit pentru ![]() x
x![]() [0,1] n(
[0,1] n(![]() ,x) astfel incat
,x) astfel incat ![]() n
n![]() n(
n(![]() ,x)
,x) ![]() <
<![]() si in plus trebuie arata ca nu este posibil ca n(
si in plus trebuie arata ca nu este posibil ca n(![]() ,x) sa fie ales independent de x
,x) sa fie ales independent de x![]() [0,1].
[0,1].
![]() Dar
Dar ![]() =
=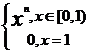
![]()
![]() Deci pentru x
Deci pentru x![]() (0,1) si n
(0,1) si n![]() 1 ,
1 ,![]() <
<![]() <=>0<xn<
<=>0<xn<![]() <=>nlg<lg
<=>nlg<lg![]() :lgx<0 caci x
:lgx<0 caci x![]() [0,1)
[0,1)
<=>n>![]()
Alegem n(![]() ,x)=max[0,[
,x)=max[0,[ ![]()
![]() Nu este posibil ca sa existe un n(
Nu este posibil ca sa existe un n(![]() ) cu n(
) cu n(![]() )
)![]() n(
n(![]() ,x) ,
,x) ,![]() x
x![]() (0,1),deoarece pentru x
(0,1),deoarece pentru x![]() 1,lgx
1,lgx![]() 0 deci
0 deci ![]()
![]()
![]() ,daca
,daca ![]() <1 => n(
<1 => n(![]() ,x)
,x) ![]()
![]() =>multimea
=>multimea ![]() este nemarginita (nemarginita!)
este nemarginita (nemarginita!)
De altfel alegand
xn=1-![]()
![]() [0,1) xn
[0,1) xn![]() 1 , =>
1 , =>![]() =
=![]() =(1-
=(1-![]() )n=[1-
)n=[1-![]() )-n]-1
)-n]-1![]()
![]()
![]() e-1=
e-1=![]() deci
deci ![]()
![]() 0 adica diferenta
0 adica diferenta ![]() nu poate fi facuta suficient de mica.
nu poate fi facuta suficient de mica.
![]()
Exemplu2 [ Sir de functii uniform convergente pe mumltimea D de functii]
![]() ,fn :[0,
,fn :[0,![]() ]
]![]() ,fn(x)=xn,
,fn(x)=xn,![]() n
n![]() 1. xn,n
1. xn,n![]() 1,x
1,x![]() [0,
[0,![]() ]
]
fn![]() f,unde f :
[0,
f,unde f :
[0,![]() ]
]![]() este functia definita prin f(x)=0,
este functia definita prin f(x)=0,![]() x
x![]() [0,
[0,![]()
![]() Intr-adevar,fie
Intr-adevar,fie ![]() >0.Cum
>0.Cum ![]() =xn<
=xn<![]() <
<![]() <=>nlg
<=>nlg![]() <lg
<lg![]() =>n>
=>n>![]()
(am tinut cont ca lg![]() <0)
<0)
![]() Aleg n
Aleg n![]() =max(0,[
=max(0,[![]() ]+1) si
rezulta ca
]+1) si
rezulta ca ![]() n
n![]() n(
n(![]() ) si
) si ![]() x
x![]() [0,
[0,![]() ] =>
] =>![]() <
<![]() =>fn
=>fn![]() f.
f.
Exemplu3 [SERIE de functii SIMPLU CONVERGENTE pe multimea D de definitie,fara a fi si UNIFORM CONVERGENTA pe D]
Seria de functii ![]() cu fn(x)=cos
cu fn(x)=cos![]() - cos
- cos![]() ,x
,x![]()
![]()
![]() n
n![]()
![]() x
x![]()
![]() are suma
punctuala(!atentie corector nu stiu daca e corect!)
are suma
punctuala(!atentie corector nu stiu daca e corect!)
S(x)=-cosx ; x![]()
are sirul (sn)n![]() 1 al sumelor partiale simplu convergent pe D=
1 al sumelor partiale simplu convergent pe D=![]() , fara a fi uniform convergent pe D.
, fara a fi uniform convergent pe D.
![]() Intr-adevar,sn(x)=f1(x)+f2(x)++fn(x)=(cos
Intr-adevar,sn(x)=f1(x)+f2(x)++fn(x)=(cos![]() - cos
- cos![]() )+(cos
)+(cos![]() - cos
- cos![]() )++(cos
)++(cos![]() - cos
- cos![]() )=
)=
=cos![]() - cos x
- cos x
![]()
Rezulta ca ,![]() x
x![]() ,
,![]() sn(x)=-cosx, deci seria considerata este simplu
convergenta la s(x)=-cosx , S :
sn(x)=-cosx, deci seria considerata este simplu
convergenta la s(x)=-cosx , S :![]()
![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1296
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved